Приведение многослойных ограждающих конструкций к однослойным при тепловых расчетах
Автор: Васильев Юрий Сергеевич, Крестьянкин Дмитрий Владимирович, Нагорная Анастасия Николаевна, Панферов Владимир Иванович
Рубрика: Инженерное оборудование зданий и сооружений
Статья в выпуске: 12 (112), 2008 года.
Бесплатный доступ
Рассмотрен вопрос приведения многослойных ограждений к однослойным при выполнении тепловых расчетов. Выполнен анализ состояния рассматриваемого вопроса в науке на сегодняшний период времени. Предложен алгоритм приведения двух и трехслойных однослойным и определения эквивалентного коэффициента температуропроводности. Для реализации данного алгоритма предлагается разработанное программное обеспечение. Для примера приводится расчет двух и трехслойной стеновой панели, приводятся графики распределения температур по толще ограждений.
Короткий адрес: https://sciup.org/147154195
IDR: 147154195 | УДК: 669.074
Текст научной статьи Приведение многослойных ограждающих конструкций к однослойным при тепловых расчетах
Рассмотрен вопрос приведения многослойных ограждений к однослойным при выполнении тепловых расчетов. Выполнен анализ состояния рассматриваемого вопроса в науке на сегодняшний период времени. Предложен алгоритм приведения двух и трехслойных однослойным и определения эквивалентного коэффициента температуропроводности. Для реализации данного алгоритма предлагается разработанное программное обеспечение. Для примера приводится расчет двух и трехслойной стеновой панели, приводятся графики распределения температур по толще ограждений.
В настоящее время в современном строительстве широкое применение находят слоистые ограждающие конструкции: стеновые панели, покрытия, ограждения для тепловыделяющих агрегатов, теплоизоляционные конструкции различных систем и т.д.
Применение различных материалов, образующих многослойные конструкции, вызывают необходимость широко заниматься не только их теплофизическими свойствами, но и расчетами температурных полей при разнообразных факторах теплового воздействия. Задача определения температуры в теле ограждающей конструкции представляет интерес как с точки зрения определения прогревания конструкции, так и при выборе наиболее благоприятной схемы расположения неоднородных слоев относительно друг друга.
При расчете тепловых режимов помещений обычно принимается, что теплотехнические характеристики материалов и воздуха практически не зависят от температуры и редко от пространственной координаты. Поэтому обычно ограничиваются моделью в виде линейного дифференциального уравнения теплопроводности с постоянными коэффициентами. Однако при рассмотрении многослойной конструкции необходимо решать уравнение теплопроводности для каждого слоя и стыковать их между собой на границе слоев, используя граничные условия 4-го рода. Вследствие чего процесс решения оказывается достаточно сложным. В связи с этим, можно добиться значительного упрощения расчетов, если найти возможность приведения многослойных конструкций к однослойным.
Решением данной задачи занимались и ранее. В работе Б.Ф. Шкурко и В.П. Начаева [1]
разрабатывается инженерный метод расчета плоских многослойных конструкций. В основу метода положена идея о приближенном приведении теплофизических характеристик материалов многослойных конструкций к эквивалентным характеристикам однослойных. Условия эквивалентности, на основе которых можно получить выражения для определения эквивалентных теплофизических характеристик материалов многослойных конструкций, зависят от условий теплообмена и целей расчета.
В работе авторами были найдены наиболее рациональные условия, которые применимы для выполнения расчетов процесса теплообмена при рассматриваемом граничном условии и обеспечивают меньшую погрешность. К ним относятся: условия равенства температур поверхностей одно-и двухслойных конструкций и условие равенства скоростей изменения температурных режимов одно- и двухслойных конструкций.
В результате реализации этих условий получены зависимости, позволяющие рассчитать эквивалентные значения коэффициентов температуропроводности и теплопроводности. Однако для численного нахождения данных величин необходимо предварительно определить эмпирические коэффициенты. С этой целью предлагается использовать приведенные в работе графические зависимости. Вследствие чего, предложенный метод нельзя назвать универсальным. Кроме того, представленный метод разработан только для двухслойной стенки.
В.А. Макагонов в своей работе [2] предлагает выражение среднего значения величины коэффициента температуропроводности для многослойной конструкции ау ^Т/1, nAi= 1,2,...,и), где п - число слоев в конструкции.
Очевидно, что предложенное выражение весьма упрощенное, и может использоваться только для приближенных расчетов температурных полей.
Для нахождения общей условной толщины конструкции автор выразил поперечный размер условных слоев через первый слой при условии равенства коэффициента температуропроводности для каждого слоя
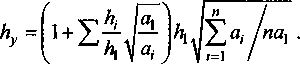
Таким образом, вместо многослойной конструкции была получена однослойная с условными значениями ау и hy.
Сложнее обстоит задача с нахождением распределения температуры в теле конструкции. Для этих целей В.А. Макогонов использовал метод приведения.
Математическая формулировка задачи включает уравнение теплопроводности, начальные и граничные условия. Далее автор переходит к безразмерному виду и, используя операционный метод, находит решение задачи в изображениях. Затем выполняется переход от изображения функций к их оригиналам, в результате чего с помощью условий приведения записывается выражения для распределения температуры в приведенной однослойной конструкции.
Используя предложенное выражение достаточно трудоемко получить численные значения температур, а ошибка вычисления, по словам автора, составляет около 12 % при малых значениях критерия Fo; при увеличении критерия ошибка также возрастает.
Таким образом, вопрос приведения многослойных ограждающих конструкций к однослойным поднимается достаточно часто при выполнении тепловых расчетов ограждений. Это связано с тем, что решение теплотехнических задач для каждого слоя в отдельности и дальнейшая стыковка их между собой является весьма сложной и трудоемкой процедурой. Как правило, требуется найти эквивалентные характеристики для однослойных ограждений, а также распределение температуры по толщине, при условии, что поведение приведенной однослойной конструкции будет совпадать с поведением многослойной. Однако, как видно из рассмотренных работ, поставленная задача в настоящее время остается окончательно нерешенной; авторами не представлен алгоритм приведения многослойных ограждающих конструкций к однослойным, а лишь показывается возможность построения такого алгоритма.
Известно, что решение уравнения теплопроводности можно представить в виде ряда Фурье по собственным функциям. Поведение решения на бесконечности определяется первым членом ряда Фурье, который убывает как экспонента. В таком случае можно принять в качестве эквивалентной однослойной модели такую модель, в которой порядок убывания первого члена совпадает с порядком убывания первого члена для многослойной стенки. Исходя из данного предположения, получили алгоритм для определения эквивалентного коэффициента температуропроводности.
Для того чтобы приводить многослойные конструкции к однослойным, выясним, как записывается решение в виде ряда Фурье для однослойной стенки и каков характер убывания первого члена в разложении для однослойной стенки.
Решение любой линейной задачи теплопроводности выписывается в виде ряда Фурье, состоящего из собственных функций решения однородной задачи [3]. Температурное поле внутри ограждающей конструкции описывается уравнением теплопроводности:
dt^x,^ 52/(х,т)
8т
8х2
где t - температура в ограждающей конструкции; т - время; х - координата; а - температуропроводность материала стенки.
Граничные условия у правой и левой поверхности стенки:
И =0; d = 0. (2)
Решение задачи методом Фурье после разделения переменных будет иметь вид:
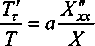
Левая часть уравнения может зависеть только от времени или быть постоянным числом, но она не зависит от координаты. Правая часть может зависеть только от координаты или быть постоянным числом, но она не зависит от времени. Равенство должно иметь место при любых значениях времени и координат. Это возможно только в том случае, если правая и левая части равенства равны некоторой постоянной величине D. Постоянная D выбирается из физических соображений. Для тепловых процессов, стремящихся к температурному равновесию, когда по истечении длительного промежутка времени (т -> оо ) должно установиться определенное распределение температуры, величина D не может быть положительной величиной, она будет только отрицательной [3].
Положим D = -к2 , где к - некоторая положительная постоянная, которая определяется из граничных условий. Тогда
Т^т^Се^;
у" а—— = -к .
X
Характеристическое уравнение для определения значения к имеет вид:
sinf .
Собственное значение числа к
, 4атгп
Общее решение задачи, представленной уравнениями (1Р(2) записывается в виде:
t(x,r) = Ve"^ rSsinf-т=х я=1 VnU )
Характер убывания определяется множителем при времени в показателе экспоненты первого члена ряда поэтому в дальнейшем будем считать эквивалентными стенками такие, у которых эти множители в показателях совпадают.
Таким образом, будем приравнивать порядки убывания решений многослойных конструкций к параметру кх, и из полученного равенства находить коэффициент температуропроводности эквивалентной однослойной стенки.
От однослойной перейдем к двухслойной стенке. Выведем уравнения, с помощью которых по известным характеристикам двухслойной стенки можно определить эквивалентный параметр температуропроводности а однослойной стенки. Эти уравнения можно определить из соответствующей однородной краевой задачи для двухслойной стенки.
Температурное поле внутри ограждающей конструкции описывается уравнением (1), где коэффициент температуропроводности материала стенки изменяется в следующем диапазоне:
Га], 0<х<1х;
а = 1
<х<Ц + 12, где /ь /2 - толщина первого и второго слоя ограждения.
Граничные условия у правой и левой поверхности ограждающей конструкции:
'L-»; 'Ц«,=°- го
В точке соприкосновения слоев выполняются условия 4-го рода:
где \, Х^- теплопроводность материала первого и второго слоя ограждения.
Характеристическое уравнение для определения собственного значения к имеет вид:
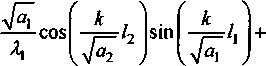
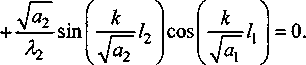
Собственных значений к , удовлетворяющих
этому уравнению, бесконечно много. Частными решениями поставленной задачи будут
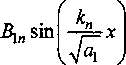
cos
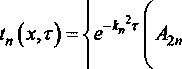
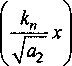
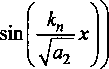
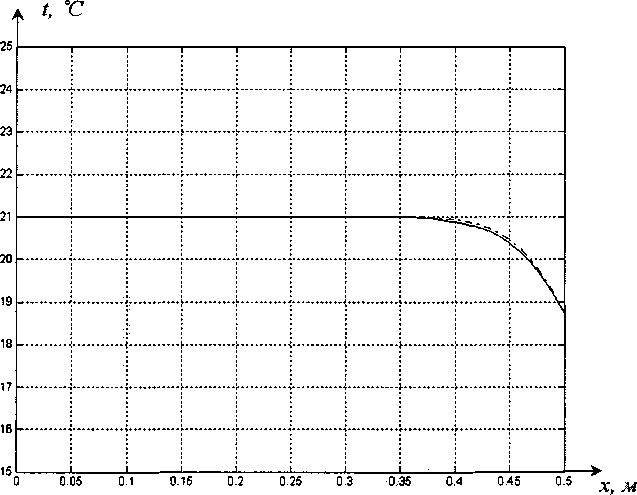
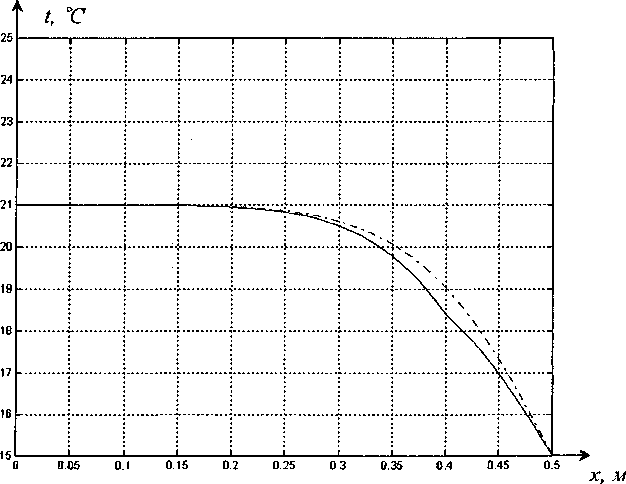
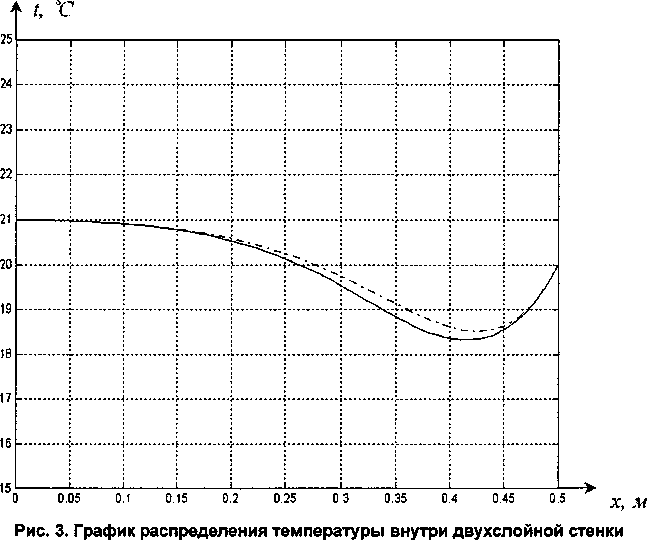
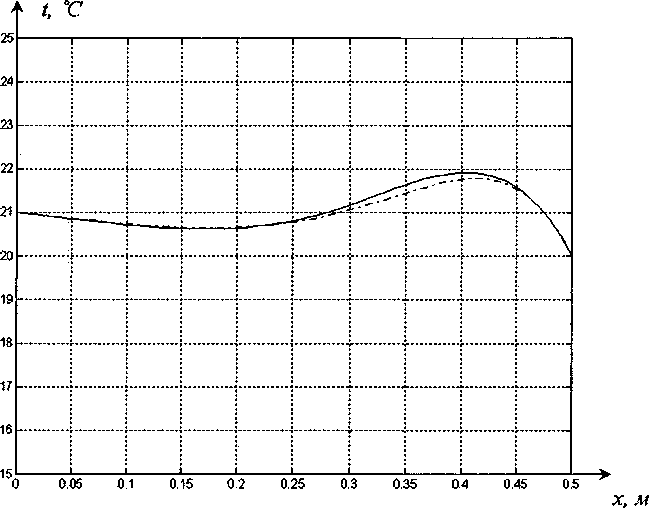
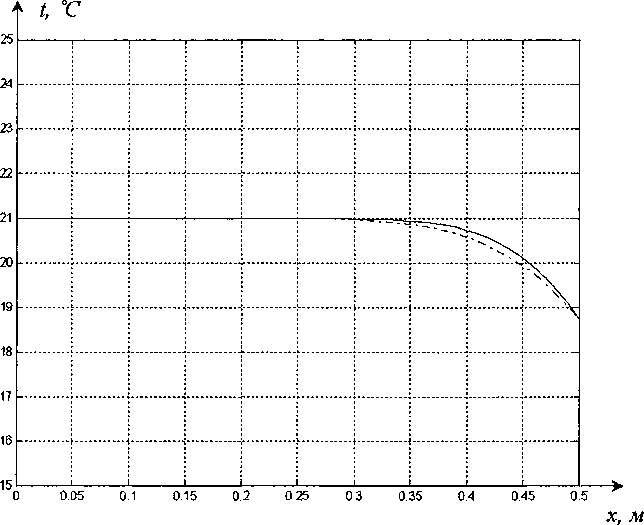
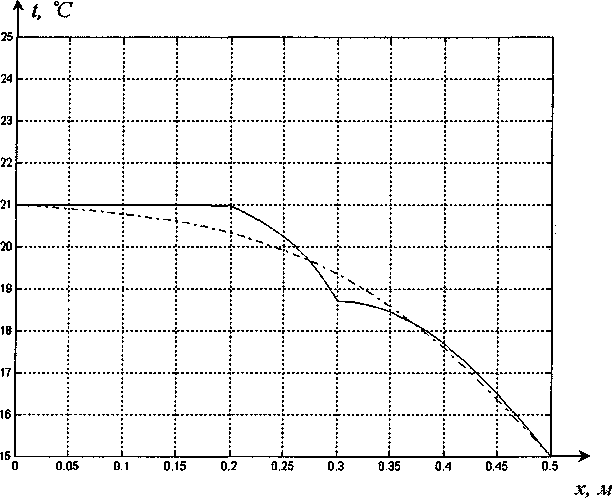
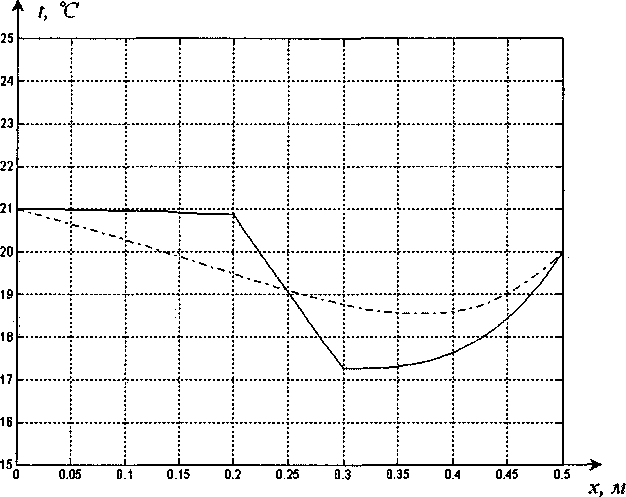
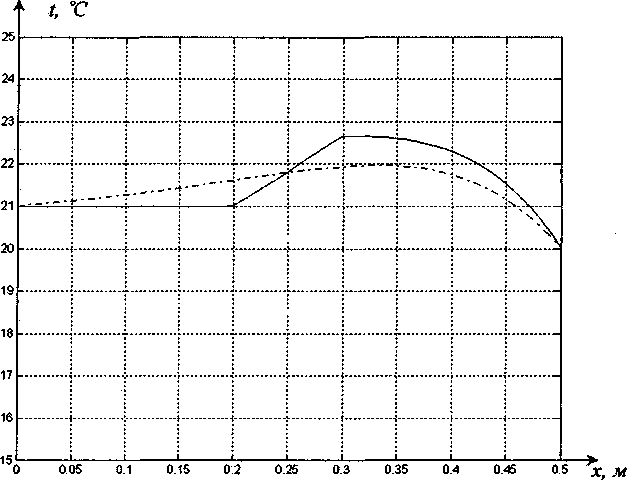
/] Тогда общее решение записывается в виде: ^(^т) = £?п(х,т). И=1 Порядок убывания определяется слагаемым, в котором показатель в экспоненте наименьший, т.е. /](х,т). Положим 0 = кх. Тогда для определения эквивалентных параметров однослойной стенки следует, зная параметры двухслойной стенки найти наименьшее положительное 0 удовлетворяю щее уравнению и приравнять его к параметру однослойной стенки к, определяемому по выражению (3). Для нахождения наименьшего собственного значения, необходимо отделить данный корень. Промежуток отделения [Д,^] первого корня уравнения (8) определяется согласно следующему алгоритму: если -4= > —0= , тогда 0Х = Vai Na2 к 12 о если —2= < , тогда 0Х = 02 =min Алгоритм получения характеристик однослойной стенки по заданным характеристикам двухслойной Имеется ограждающая конструкция, состоящая из двух слоев. Первый слой имеет толщину 1Х. Материал первого слоя ограждающей конструкции имеет теплопроводность ^, плотность рх, теплоемкость сх. Второй слой имеет толщину /2. Материал второго слоя ограждающей конструкции имеет теплопроводность ^, плотность рг , тепло емкость с2. Требуется получить эквивалентную однослойную стенку толщины I = lx +/2, то есть найти эквивалентный параметр а. Исходя из вышеизложенного можно выписать следующий алгоритм. 1. Положить ширину однослойной стенки / = /1+/2. [Д,Д] = иначе LW2] = mm^-—;—— /2 2 А 3. Найти корень р уравнения на интервале [А,А1- Разработка программных средств Для реализации полученного алгоритма составлена программа 21ayers.m в математическом пакете Matlab [4], которая работает по следующему алгоритму: 1) определение констант: - теплопроводности ^, плотности рх, теплоемкости С], толщины А первого слоя ограждающей конструкции; - теплопроводности ^, плотности р^, теп лоемкости с2, толщины /2 материала второго слоя конструкции; - температуры воздуха внутри помещения и ограждающей конструкции; - длительности моделируемых процессов Т; 2) вычисление ширины эквивалентной стенки / = /1+/2; 3) если -== > —== , полагается [А,А1 = иначе [А,А1 = 4) нахождение корня р уравнения на интервале [Д, Д ]; 5) вычисление коэффициента температуро- проводности а по формуле а = I -— I ; V it ) 6) решение задачи теплопроводности для однослойной стенки с коэффициентом температуропроводности а неявной разностной схемой; 7) решение задачи теплопроводности для двухслойной ограждающей конструкции неявной разностной схемой; 8) построение графиков распределения температуры внутри стенок через 1, 6,12,24 часа. Пример использования алгоритма Имеется ограждающая конструкция, состоящая из двух слоев. Первый (внутренний) слой имеет толщину 1Х =0,1м и состоит из пустотного керамического кирпича, имеющего следующие теплотехнические показатели: теплопроводность Д =0,47 Вт/(м-°С), теплоемкость с, = 880 Дж/(кг °С), плотность рх =1600 кг/м3. Второй (наружный) слой имеет толщину /2=0,4м и состоит из силикатного кирпича, имеющего следующие теплотехнические показатели: теплопроводность Д =0,7 Вт/(м-°С), теплоемкость с2 =880 Дж/(кг °С), плотность р^ =1800 кг/м3. Температура воздуха внутри помещения постоянна и равна 21 °C. Температура наружного воздуха изменяется по периодическому закону L (г) = 20 — 5sin[ 1к-------I, 7 ( 24-3600) где т - время в секундах. В начальный момент времени температура внутри стенки на всем протяжении равна 21 °C. Вычислим коэффициент температуропроводности эквивалентной однослойной по представленному алгоритму: а = 3,8319 • 10-7 м2/с . Построим графики распределения температуры внутри стенки. На всех графиках сплошной линией обозначается распределение температуры внутри двухслойной стенки, штрихпунктирной линией - распределение температуры внутри однослойной стенки с коэффициентом температуропроводности а (рис. 1-4). На графиках видно, что способ вычисления коэффициента температуропроводности эквивалентной однослойной стенки дает хорошее приближение к двухслойной стенке. Используя аналогичный подход разработан алгоритм приведения трехслойной стенки к однослойной и вычисление эквивалентного коэффици ента температуропроводности. Для реализации алгоритма написана программа 31ayers.m в математическом пакете Matlab [4], логическая структура которой следующая: 1) определение констант: - теплопроводности ^, плотности рх, теплоемкости q, толщины /, первого слоя ограждающей конструкции; - теплопроводности ^ , плотности р^ , теплоемкости с2, толщины Z2 материала второго слоя конструкции; Рис. 1. График распределения температуры внутри двухслойной стенки в момент времени г = 1 ч Рис. 2. График распределения температуры внутри двухслойной стенки в момент времени г = 6 ч в момент времени г = 12 ч Рис. 4. График распределения температуры внутри двухслойной стенки в момент времени г = 24 ч - теплопроводности Яд, плотности р3, теплоемкости с3, толщины /3 материала третьего слоя конструкции; - температуры воздуха внутри помещения и ограждающей конструкции; - длительности моделируемых процессов Т; 2) вычисление ширины эквивалентной стенки I = /^ +I2 + Z3; 3) вычисление промежутка отделения корня [А, А]; 4) нахождение корня р уравнения f(,P3 = ^2^4^\4^2. cos—^=/2 cos—^=/3 + . . р , . р , р , +х1Л3а2 cos—у=/] sin—^=/2 cos—^=/3 + Val Va2 N°3 +Й1Я2 V^T cos~7= k cos ^2 s™ ~т= к V а1 Va2 Va3 -^^^^/^sin-^Zj sin-^/2 sin—~/3 =0 Na2 \a3 на интервале YP\> А ] i 5) вычисление коэффициента температуро-. (Р*Г? проводности а по формуле a = I -— I ; V л- ) 6) решение задачи теплопроводности для од нослойной стенки с коэффициентом температуропроводности а неявной разностной схемой; 7) решение задачи теплопроводности для трехслойной ограждающей конструкции неявной разностной схемой; 8) построение графиков распределения температуры внутри стенок через 1, 6,12,24 часа. Пример реализации алгоритма Имеется ограждающая конструкция, состоящая из трех слоев. Рис. 5. График распределения температуры внутри трехслойной стенки в момент времени т = 1 ч Рис. 6. График распределения температуры внутри трехслойной стенки в момент времени г = 6 ч Первый (внутренний) слой имеет толщину /, = 0,2 м и состоит из железобетона, имеющего следующие теплотехнические показатели: теплопроводность 2, = 1,69 Вт/(м-°С), теплоемкость Cj = 840 Дж/(кг-°С), плотность р^ = 2500 кг/м3. Второй (промежуточный) слой имеет толщину /2 =0,1 м и состоит из пенополистирола, имеющего следующие теплотехнические показатели: теплопроводность ^ = 0,05 Вт/(м-°С), теплоемкость с2 = 1340 Дж/(кг-°С), плотность рг =150 кг/м3. Третий (наружный) слой имеет толщину /3 =0,2м и состоит из железобетона, имеющего следующие теплотехнические показатели: теплопроводность 2j =1,69 Вт/(м °С), теплоемкость с3 = 840 Дж/(кг-°С), плотность р3 = 2500 кг/м3. Температура воздуха внутри помещения постоянна и равна 2 ГС. Температура наружного воздуха изменяется по периодическому закону c(r) = 20-5sin 2л------- 7 I 24-3600 где т - время в секундах. Рис. 7. Г рафик распределения температуры внутри трехслойной стенки в момент времени г = 12 ч Рис. 8. Г рафик распределения температуры внутри трехслойной стенки в момент времени г = 24 ч В начальный момент времени температура внутри стенки на всем протяжении равна 21 °C. Вычислим коэффициент температуропроводности эквивалентной однослойной по представленному алгоритму: a = 1,1886-КГ6 м2/с. Построим графики распределения температуры внутри стенки. На всех графиках сплошной линией обозначается распределение температуры внутри трехслойной стенки, штрихпунктирной линией - распределение температуры внутри однослойной стенки с коэффициентом температуропроводности а (рис. 5-8). На полученных графиках видно, что поведение построенной по алгоритму эквивалентной однослойной ограждающей конструкции похоже на поведение многослойной.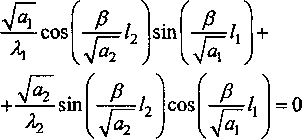
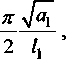
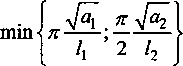
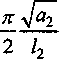
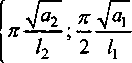
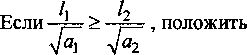
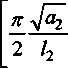
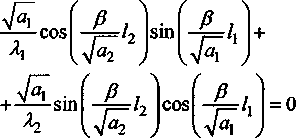
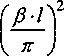
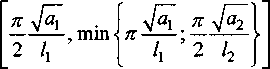
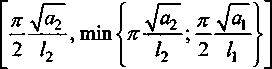
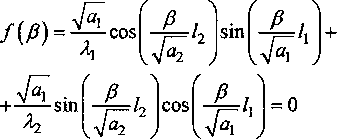
Список литературы Приведение многослойных ограждающих конструкций к однослойным при тепловых расчетах
- Шкурко Б.Ф. К вопросу инженерного теплового расчета конструкций/Б.Ф. Шкурко, В.П. Нечаев//Изв. вузов. Серия «Строительство и архитектура». 1985. № 3. С. 93-96.
- Макогонов В.А. О возможности приведения многослойных конструкций к однослойным при тепловых расчетах/В.А. Макогонов//Изв. вузов. Серия «Строительство и архитектура». 1974. № 4. С. 137-140.
- Лыков А.В. Теория теплопроводности/А.В. Лыков. М.: Высш. шк., 1967. 599 с.
- Кондратов В.Е. MATLAB как система программирования научно-технических расчетов/В.Е. Кондратов. М.: Мир, 2002. 350 с.


