Приведение статических характеристик комплексной нагрузки к узлу электрической сети по данным измерений в удаленных узлах

Знание статических характеристик нагрузки (СХН) важно для решения многих задач проектирования и управления в системообразующих и распределительных сетях. В сетях 35–220 кВ правильное моделирование нагрузки и точное определение коэффициентов моделей позволяет решать не только технические задачи, такие как поддержание устойчивости сетей [1, 2], но и техникоэкономические задачи по организации оптимальных перетоков мощности [3, 4]. В распределительных сетях СХН важны для определения оптимальных условий компенсации реактивной мощности [5] и управления сетями [6].

Определение коэффициентов СХН обсуждается в работах, выполненных как на основе симуляционных моделей сетей [7], так и реальных экспериментальных данных [8, 9].

Как показал опыт экспериментального определения коэффициентов СХН в РФ [10–13], наиболее точным и эффективным, но не всегда возможным является проведение активного эксперимента, суть которого заключается в принудительном изменении напряжения потребителя и регистрации изменения его активной и реактивной мощности. На практике реализация данного подхода встречает массу затруднений. Поскольку эксперимент проводится на действующем энергообъекте, достижимый диапазон изменения напряжения ограничивается допустимыми предельными значениями для сохранения нормальной работы данного потребителя или группы потребителей. Режим работы и состав электроприемников потребителей может измениться в течение эксперимента. Для некоторых типов нагрузок (электрометаллургия, горнодобывающая промышленность и др.) это изменение может составлять сотни процентов [14].

Постановка задачи

Таким образом, измерение СХН является достаточно сложной задачей. При проведении экспериментов, как правило, используется ограниченное количество измерительных приборов необходимого класса точности. Кроме того, могут возникать сложности с доступом, если объект находится в собственности другой организации.

Наиболее часто возникает необходимость в расчете СХН на высоком напряжении трансфор-

матора по измеренной характеристике (характеристикам) на низком напряжении двухобмоточного трансформатора (трехобмоточного трансформатора или трансформатора с расщепленными обмотками). Практический опыт авторов по измерению СХН по заказам организаций показывает, что не всегда есть возможность подключения сертифицированного измерительного оборудования одновременно на стороне высокого и низшего напряжения подстанции. Это может быть связано как с доступом к измерительным цепям первичных датчиков, так и наличием требуемого количества измерительного оборудования. Однако Заказчику требуется получить СХН как на низком, так и на высоком напряжении трансформатора, и, следовательно, оборудования для проведения измерений за один допустимый активный эксперимент просто недостаточно. Для проведения исследований понадобится повторение эксперимента, что, как правило, не приветствуется и собственниками подстанции, и потребителями, подключенными к ней.

Поэтому возникает необходимость получения СХН расчетным путем для точек (узлов) систем электроснабжения, ближайших к тем, в которых проведены измерения. Методика пересчета должна быть общей, поскольку в реальных сетях промышленных предприятий возникают весьма экзотические варианты соединения трансформаторов и токоограничивающих реакторов. Далее рассмотрена методика пересчета СХН, отвечающая указанным требованиям.

Методика расчета

Разделим произвольный элемент СЭС на элементарные многополюсники, соответствующие узлу сети и ветви сети. Произвольную ветвь схемы можно смоделировать при помощи двух четырехполюсников, показанных на рис. 1.

Пусть для четырехполюсника (рис. 1а) известны величина напряжения U ₂, тока I ₁ = I ₂, активной P ₂ и реактивной Q ₂ мощности нагрузки. Также известно комплексное сопротивление Z = R + jX четырехполюсника. Используя баланс активных и реактивных мощностей, а также выражения для треугольника мощностей для входа и выхода четырехполюсника, получим напряжение U ₁, активную P ₁ и реактивную Q ₁ мощности на входе четырехполюсника:

р^)^

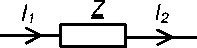
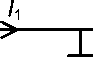
U2

-> РгШ м^С^

P i( Ui)^

Q i( Ui)^

U 1 v

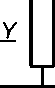
U 2

-> P 2 ( U 2 ) ,^ Q 2 ( U 2 )

а)

b)

Рис. 1. Элементарные четырехполюсники

Fig. 1. Elementary four-poles иi = и2

P ² + Qi.

\ PH + Q 2 ;

P i = P 2 + R^"-                 (1)

U ₂

Q = Q + X^ .

U 2 ²

Пусть для четырехполюсника (рис. 1b) известны: величина напряжения U ₂, активной P ₂ и реактивной Q ₂ мощности нагрузки. Также известна комплексная проводимость Y = G + jB четырехполюсника. Активная P ₁ и реактивная Q ₁ мощности, а также величина напряжения U 1 на входе четырехполюсника определяются в виде:

P i = P 2 + GU 2 ; Q i = Q 2 + BU 2; U 1 = U 2 .   (2)

Полученные выражения (1) и (2) позволяют вычислить функции СХН для входа элементарного четырехполюсника P ₁ ( U ₁ ) и Q ₁ ( U ₁ ) по известным

Также в качестве узла может рассматриваться идеальный трехобмоточный трансформатор или трансформатор с расщепленными обмотками. В этом случае уравнения (3) дополняются уравнениями идеального трансформатора

U _i = К Т ₂U ₂ = К Т3 U 3 . (4)

Пример использования методики

В качестве примера приведем пересчет статических характеристик нагрузки с обмоток низкого и среднего напряжения трехобмоточного трансформатора на обмотку высокого напряжения.

Исходными данными являются измеренные

СХН для низкого напряжения

P ₂ ( U ₂) = A ₂ + B₂U ₂ + C₂U ₂²;

Q ₂( U ₂) = a ₂ + b ₂ U ₂ + c ₂ U ₂ ²

статическим характеристикам нагрузки для выхода четырехполюсника P ₂( U ₂) и Q ₂( U ₂) . Таким образом, можно смоделировать линию электропередачи или двухобмоточный трансформатор, т. е. любую ветвь системы электроснабжения, в виде каскадного соединения элементарных четырехполюсников (см. рис. 1). Последовательно применяя формулы (1) или (2), можно получить СХН для входа четырехполюсника по характеристике для его выхода. Пересчет характеристик можно осуществить и с входа на выход четырехполюсника, если провести несложные преобразования в выражениях (1) и (2).

Узел системы электроснабжения моделируется многополюсником. В случае соединения 3 ветвей модель представлена на рис. 2.

В качестве узла электрической сети может выступать секция шин или сдвоенный токоограничивающий реактор. В этом случае U _i = U ₂ = U 3 и пересчет характеристик определяется уравнениями баланса мощностей:

P = P > + P 3 ; Q i = Q 2 + Q 3 . (3) При необходимости количество ветвей в узле может быть легко увеличено.

и среднего напряжения

P 3 ( U 3 ) = A 3 + B 3 U 3 + C 3 U ₃²;

^Q 3^{( U} 3 ) = a 3 ^{+ b} 3 ^U 3 ⁺ c 3 ^{U 2} ,

где A ₂, B ₂, С ₂ ; A ₃, B ₃, С ₃ ; а ₂, b ₂, c ₂ ; a ₃, b ₃, c ₃ – постоянные коэффициенты СХН. Исходные характеристики для обмоток низкого (5) и среднего (6) напряжения должны быть представлены в именованных единицах (кВт, квар).

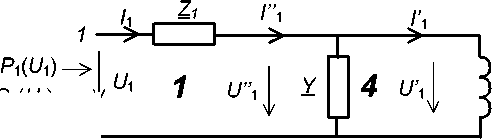
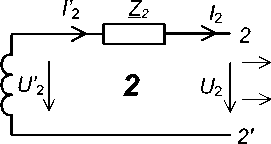
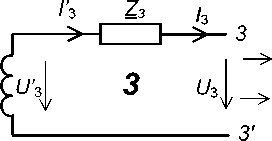
Схема замещения трансформатора изображена на рис. 3. Для получения элементов схемы замещения необходима стандартная информация о каталожных данных трехобмоточного трансформатора.

На схеме замещения (см. рис. 3) трансформатор представлен 3 четырехполюсниками, моделирующими обмотки высокого (1), низкого (2) и среднего (3) напряжения; четырехполюсником, моделирующим сердечник (4), и шестиполюсни-ком (5), моделирующим идеальный трансформатор.

Проводя объемные, но несложные вычисления, получаем СХН на обмотке высокого напряжения:

P i (U i ) = A i + B i U i + C i U i ²;

Q i ( U i ) = a i + b i U i + C i U i ².

СХН (7) также получается в именованных единицах, но при необходимости ее можно пере-

^P2^

иЧ^О2(и2)

Pi(U^

Qi(^i)^v

^P3(U3)

х/ -^Q3(U3)

Рис. 2. Модель узла сети Fig. 2. Network node model

Qi(LVi)^V

T-

P2(U2)

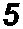
Рз(и3)

ОзМ)

Рис. 3. Схема замещения трехобмоточного трансформатора Fig. 3. Three-winding transformer replacement circuit писать в относительных единицах, выбрав базовую мощность и базовое напряжение.

Заключение

Изложенная в статье методика позволяет представить произвольный участок системообразующих или распределительных сетей 35–220 кВ в виде набора элементарных многополюсников и

получить СХН для близлежащих участков сети. Эта методика является общей и может применяться для произвольной конструкции электрических сетей. Кроме того, предлагаемая методика позволяет проводить эквивалентирование СХН для участков сети, если создается упрощенная расчетная модель, не требующая подробного рассмотрения какой-то части энергосистемы.