Приводимость и устойчивость системы линейных дифференциальных уравнений с кусочно-частичными периодическими коэффициентами

В работе [1] и [2] показано, что всякая система линейных дифференциальных уравнений с периодическими коэффициентами приводима. Отметим, что в работах [2], [3] рассмотрены некоторые очевидные классические результаты о системах линейных дифференциальных уравнений с периодическими и почти периодическими коэффициентами.

Наша работа состоит из двух частей. В первой части мы ввели понятие кусочно-частично периодической функции. Во второй показали приводимость системы линейных дифференциальных уравнении с кусочно-частично периодическими коэффициентами.

Часть 1

Определение 1. Пусть - - ■'■■ ':-i ■• 2    4 ■■. ■■' вещественная (или комплексная) функция, определенная при _;: ^ ^ : "::       :. < = 1 . ' '. Пусть ■ < ^ "       ■    ■    " . Кроме того,

т

. нерациональные числа для каждых ‘ ■ ^ - .

Функцию               назовем функцией с кусочно-частичным периодом, если верны еее А ^ — 1# A ^ t X Jf^f i..#Xm/ — J 1 > ••• I X ^ — 1, А ^ Т 1 > X к + ) > •• • ) X уп) для каждых 1       . ' ^ ■ где • - - •       .

В этом случае Т = y_v ••■ ^ назовем кусочно-частичным периодом функций ^/;i ^ -■.

х z х COs(V3y)

гСх,у, z) = cosU) + ---- . , г V                   .

Пример: Пусть                          I п¹-, ? ¹ где ⁵-^:L< ■■ ' -        . Тогда очевидно, что

( 2п \    / 2тг\

x,y + -=,z)= F(x,y,z + -=)

Поэтому функция               или

ФоМ = COs(x) 4-

cos(V3x)

2 + sin(V2x)

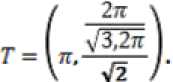
будет функцией с кусочно-частичным периодом при              причем

Замечание 1. Из определения 1 следует, что каждая вещественная (или комплексная) периодическая функция является кусочно-частично периодической функцией.

Рассмотрим систему линейных однородных дифференциальных уравнений первого порядка:

dx. v^ / Ptk№. G = 1.....n),

UI       I

k=l где Р»(ГХ<,к = 1,....п -комплексная функция вещественного аргумента t при -co < t < +» .

Ф-.к^ц •••• tm) ~ 0,k(tl, —• te-lA, + T„t,4.t —>tmy S = 1,...,771

(Это следует из определения 1)).

В этом случае систему (1) запишем так:

"57 = У ^ik^V - ^^к- i = 1. ••••”

k=l

Замечание 3. Полагая X — (.X £, .e., Л _n)j

P(0 = |0ik(t,t,...,t)l£ , систему (4)

перепишем в

виде:

dx, "dt

P(O-x

Часть 2

Лемма. Всякая система (4) с кусочно-частичными периодическими коэффициентами (с одинаковым частным периодом) приводима.

Доказательство. fll(O,...,flm(O -вещественные непрерывные функции на интервале

00 < t < +*

.

Рассмотрим систему:

dx.

n

Очевидно, что если Д о некоторая интегральная матрица системы (7) , то ■'л 6 зависит от функций 51(0, ...,flm(0 . Поэтому интегральную матрицу ^ a рассмотрим как функцию аргументов 51(0, .,5m(0 или^O=^o(51(O,..,5m(O) .

Из условия (7) следует, что ^.(51(0+ Л....._5m(0) также является интегральной матрицей системы. Рассмотрим случай, когда 51(0 = 51(0 = — = 5m(0 = t . Тогда X_e(.t.t,.„.t) имеет интегральную матрицу системы (4). Поэтому

dX0(t -t-Tvt,....t)

dt

= p(o-^e(t + r1,t,....o

и

dXe(t,t,....t)                     .

-----= P(o ■ X_e(t, t, .... 0. at

Из определения интегральной матрицы вытекает, что X_e(t*T_vt,....t') = X_e(t.t, некоторая постоянная матрица. Поскольку det(V) * 0 , то можно опеределить,

OV', где V -

Тогда L(0 = X_e(tWTt является непрерывной кусочно-частично периодической функцией с частным периодом T . В этом случаее преобразование

X = L(0 * Y является преобразованием Ляпунова и система (6) приводится к виду

Лемма доказана.

Каждая приводимая система однородных линейных дифференциальных уравнений устойчива по Ляпунову (см [1]). Поэтому из леммы следует, что каждая система однородных линейных дифференциальных уравнений с кусочно-частичными коэффициентами также устойчива по Ляпунову.