Призменный масс-спектрограф с конусовидной ахроматичной призмой и трансаксиальными линзами

Статические секторные масс-спектрометры это, как правило, приборы с тройной фокусировкой пучка ионов — по двум направлениям и энергии. Основными элементами анализаторов этих приборов являются секторный магнит и секторное электростатическое поле цилиндрического, сферического или тороидального конденсатора.

Согласно "теореме о потоке" [1], для улучшения качества статических масс-анализаторов необходимо расширять пучок ионов перед входом в магнитное поле, увеличивая магнитный поток, пронизывающий пучок ионов. Эта идея была реализована в масс-спектрометре Матсуда [2], где расширение пучка перед входом в сектор магнита осуществляется системой квадрупольных линз.

Расширение пучка перед входом в магнит можно осуществлять более эффективно, используя электростатические призменные системы, которые обеспечивают еще и фокусировку по энергии [3–5]. В этом плане уникальной конструкцией является призменный масс-анализатор с конусовидной ахроматичной призмой (КАП), обладающей рекордной угловой дисперсией по массе, равной примерно 50 рад на 100 % изменения массы [6, 7]. Линейная дисперсия такого прибора равна произведению угловой дисперсии призмы Dm на фокусное расстояние f2 фокусирующей линзы. Так, при f, «1м линейная дисперсия прибора будет равна Dm = Dmf, ~50м, что при микронных ширинах щелей источника и приемника ионов позволяет получить разрешение порядка 107.

Схема такого прибора в проекции на среднюю плоскость (горизонтальное направление) представлена на рис. 1. Здесь 1 — магнитные полюса КАП; 2, 3 — электроды и одновременно магнитные экраны КАП; V ₀ , V ₁ , V ₂ — потенциалы электродов; 4, 5, 6 — электроды коллиматорной и фокусирующей линз; 7, 8 — щели источника и приемника ионов. Как видно из рисунка, параллельный пучок ионов, входящий в КАП, сначала расширяется за счет преломления в электрическом поле, а затем происходит его расширение в неоднородном магнитном поле КАП. Так как сектор магнитного поля y_h в КАП больше 180 ° , поток магнитного поля, пронизывающий ионный пучок здесь очень большой, что и обеспечивает большую угловую дисперсию КАП.

В КАП реализуются электрическое и магнитное поля типа 1 r , потенциалы которых в сферической системе координат r , ϑ , ψ с началом в вершине конических поверхностей зависят только от угловых переменных ϑ , ψ . Как показано на рис. 1, все частицы однородного плоского параллельного пучка ионов, входящего в КАП в средней плоскости, движутся по подобным траекториям, в результате сохраняется параллельность пучка и на выходе из КАП. Причем это свойство не зависит от ширины пучка в средней

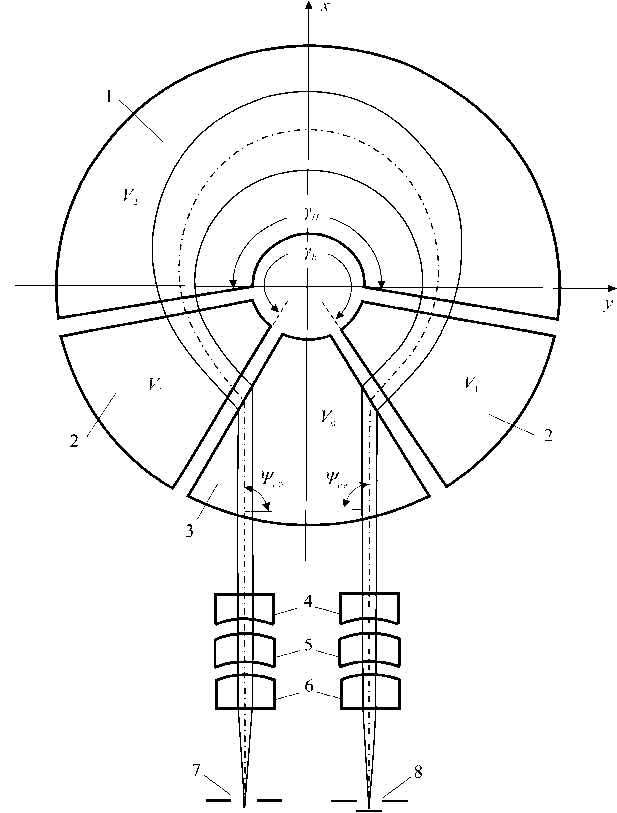
Рис. 1 . Схема призменного масс-спектрометра с КАП.

1 — полюсные наконечники; 2, 3 — магнитные экраны-электроды призмы; 4, 5, 6 — электроды коллиматорной и фокусирующей линз; 7, 8 — щели источника и приемника ионов

плоскости, поэтому увеличение ширины пучка в горизонтальном направлении не увеличивает аберрации КАП. В КАП также осуществляется фокусировка по энергии, а параллельность объемного пучка обеспечивается благодаря выполнению условия телескопичности в вертикальном направлении. Эти свойства особенно важны при использовании КАП в призменном масс-спектрометре.

Ниже рассчитываются корпускулярно-оптические свойства призменного масс-анализатора с КАП и трансаксиальными коллиматорной и фокусирующей линзами.

ЭЛЕКТРИЧЕСКОЕ И МАГНИТНОЕ ПОЛЯ КАП

ТФКП [8]:

Ф ( V , Z ) = - 2 V, - V + F (V + ^ , Z| V o , V 2 ) +

+ F 1 (V + ^YH- , z| V 2 , V ) + FAv - Y H , Z| V 1 , V ₂) +

+ F > -, Z| V 2 , V o ),                          (2)

Q ( V , Z ) =Q 1 1 V + Y H -, z

—

C ₂ C ₂

2,2

\

+

В результате введения переменной

Z = lntg 2,                 (1)

+qi I v - Yh ,z

C 2

2,

c

C ₂

потенциалы электрического Ф ( Z , V и магнитного Q ( v , Z ) полей КАП в переменных Z , V удовлтворяют двумерному уравнению Лапласа и находятся аналитически с помощью методов

Здесь γ_E , γ_H — геометрические параметры, задающие положение границ электродов, определяемых полуплоскостями V = ± Y e 1 2, V = ± Ун /2 ; V ₁ , V ₂ , V ₀ — потенциалы электродов 1, 2, 3 соответственно; внешние поверхности электродов совпадают с поверхностями прямых круговых конусов i 9 = П 2 ± X 2, как показано на рис. 2. Полюса

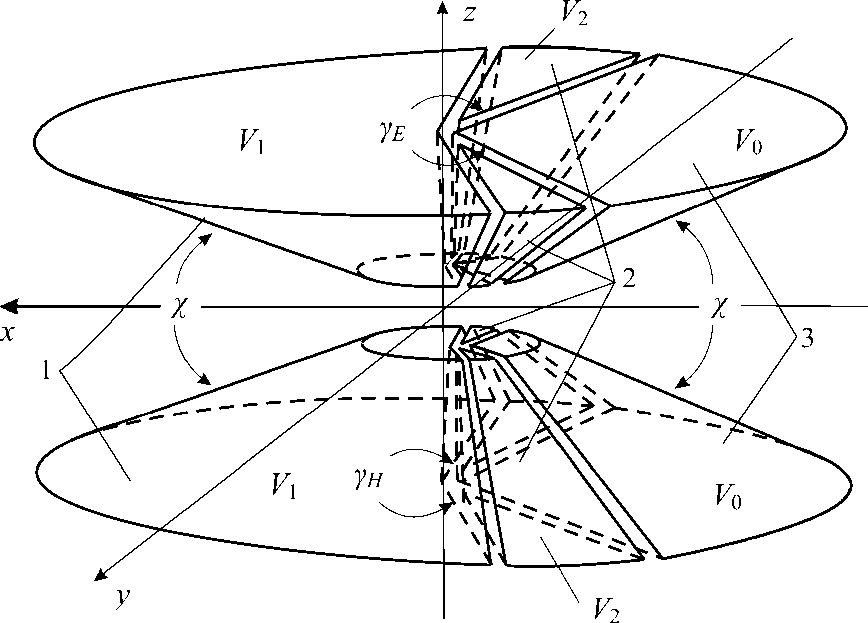
Рис. 2. Трехэлектродная КАП. Электроды 1 одновременно являются магнитными полюсами, а электроды 2, 3 — магнитными экранами; V 1 , V 2 , V 0 — потенциалы электродов

магнита 1 на поверхностях $ = — 2 ± X 2 имеют магнитный потенциал ± С ₂ соответственно, а магнитные экраны-электроды 2, 3 с бесконечно большой магнитной проницаемостью имеют магнитный потенциал — 1 = 0. Используемые в (2) и (3) базовые функции определятся следующими выражениями:

FMZ V , V 2 ) = V + V —² х π

(     1 + и 1 — и А х| arctg-----+ arctg к vv f (у) =Ф(у,0),,     h (у) — 4=0,(7)

a Z определяющие распределение электрического и магнитного полей в средней плоскости призмы Z = 0. Отметим также, что величина напряженности магнитного поля в центре магнита h(0) связана с магнитным потенциалом полюсов выражением —2 = h (0) Zk (C1 = 0), где

Z k = lntg

5 1 Z

Ц( у . Z c , , C 2 ) = -I----2- х

π

БЕЗРАЗМЕРНЫЕ УРАВНЕНИЯ НЬЮТОНА

х

1 + и arctg

v

1 — и — arctg---- v

—

2 C u

¹ arctg ,

π

v

где

При расчете траекторий заряженных частиц с зарядом e и массой m в призменном масс-анализаторе используются безразмерные уравнения Ньютона, которые в декартовых координатах х , y , z можно записать в следующем виде:

и = и (у, Z ) =— exp

П

у к 2 Zk  )

sin

^— к 2 Z k

А

Z

)

v = v ( у , Z ) = exp

^П к 2- ^у

)

cos π ζ к 2 ZX

к

)

x =ФХ+ yQz— zQ , xzy

y =Ф+ z Qx— x Qz, yxz

Используя выражения для потенциаллов можно найти функции

z =Ф2+ xQ -yQ .

zyx

Здесь Ф=— фV ₀ — безразмерный электростатический потенциал, а Q — безразмерный магнитный потенциал; индексы при Ф и Q обозначают

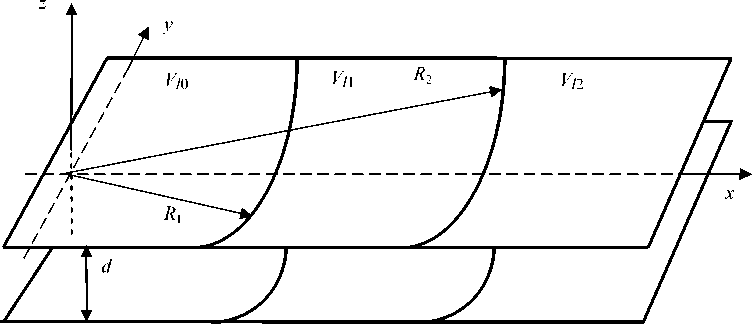
Рис. 3 . Схематическое изображение трансаксиальной линзы

частные производные по соответствующим безразмерным декартовым координатам; за единицу длины берется величина d — расстояние между параллельными плоскостями трансаксиальных линз (см. рис. 3); точки обозначают производные по безразмерному времени т = t/т 0 , где

=—arctg π

π

2cos z d

π R d

Р I

к RkJ

—

π R .

( n A^— ^

р I

к Rk J

τ ₀

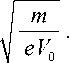
Функции

^Pk Р . z . R к ^Rk     J

( k = 1.2) зависят также

от параметра R = ^ R 1 R ₂ . Формулы (11). (12) дают

РАСЧЕТ ТРАНСАКСИАЛЬНОЙ ЛИНЗЫ

Трехэлектродная трансаксиальная линза схематически изображена на рис. 3, где показана также сопутствующая декартова система координат x, y, z с началом в средней плоскости линзы xy . Здесь R ₁ и R ₂ — радиусы границ электродов; V_{l 0} , V_{l 1} и V_{l 2} — потенциалы электродов линзы, d — расстояние между пластинами.

В цилиндрических координатах потенциал поля линзы зависит от переменных р = ^ x ² + у ² , z и с хорошей точностью может быть записан в следующем виде:

простое аналитическое выражение для электростатического потенциала трехэлектродной трансаксиальной линзы, удобное для проведения численных расчетов.

Расчет траекторий частиц в трансаксиальной коллиматорной линзе также проводился путем численного интегрирования уравнений (9). Начальные условия для частиц задавались следующим образом:

x 0 = l . | y o| <  а . | z o| <  b . | ^y o| <  V 2(1 ⁺ S ) sin ^a. (13) | ^^0 1 <  V ^{2(1 + S} ) sin ^e, x ^ o = 7 ^{2(1 + S} ) ^— y o^{2 —} z o² .

где

Ф(р,z ) = V + ( V , - V_x ) P 1

(а     I

Р , z , R Г к R 1      J

г

+

( V - V ₂ ) р ₂ Р , Z , R | , к R

P k

(

Р . z . ^R к ^Rk

Здесь ε — относительный разброс по энергии на входе в коллиматорную линзу; постоянные a и b определяют ширину и высоту источника ионов; углы α и β определяют разброс частиц по направлению вылета из источника в горизонтальном и вертикальном направлениях соответственно.

Была рассчитана эмиссионная трансаксиальная линза в режиме анаморфота, которая имеет следующие параметры: R 1 = 1o d и R 2 = 13.2 d ; V_{l o} = 1. V _n = o.o68 и V_{l 2} = o.4 с фокусным расстоянием. примерно равным f 1 = 2o d .

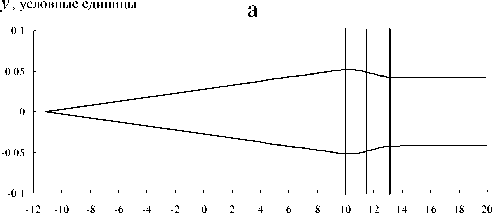
z , условные единицы

б

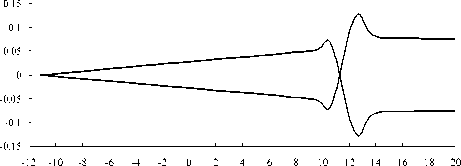
x , условные единицы                                                        x , условные единицы

Рис. 4 . Ход ионных траекторий в коллиматорной линзе в проекциях на горизонтальное (а) и вертикальное (б) направления

РАСЧЕТ ПРИЗМЕННОГО МАСС-АНАЛИЗАТОРА

Рассматривались пучки в анализаторе с осевой траекторией, симметричной относительно плоскости xz . Геометрические и полевые параметры конусовидной призмы подбирались так, чтобы выполнялись условия ахроматичности и телескопич-ности. Такую призму мы и называем КАП (конусовидная ахроматичная призма). КАП задается следующими параметрами: х = 5 ° , Y H = 208 ° , Y E = 294.77 ° , V/V 0 = 16.6482, С ₂ = 0.3143, кривизна осевой траектории в центре магнита k m = 12.3964. На входе в призму угол наклона осевой траектории к оси у равен Т с ₀ = 81.69781 ° . Относительный энергетический разброс в источнике изменялся в интервале s = ± 0.01, угловая дисперсия по энергии D S <  0.002. Координаты частиц на входе в призму преобразовывались в декартовы координаты, связанные с КАП. Точка входа осевой траектории в КАП в этих координатах: x ₀ =- 15.0, у ₀ =- 3.90061.

Отметим также, что при расчетах потенциалы электродов призмы умножаются на V 2 = 0.4, т.к. потенциалы на выходе из коллиматорной линзы V_{l 2} и на входе в КАП V ₂ одинаковы. Разница в массах частиц задавалась путем изменения потенциала магнитного поля: С ₂ ^ С ₂ ^ ( 1 + у ) V ₂ .

Угловые хроматические аберрации КАП можно описать следующей формулой, определяющей изменение угла выхода частицы из КАП:

АТ = D' s + А s ² + А s 3 . (14) хр 2 3

Эта формула справедлива вплоть до значений s = ± 0.1. Здесь коэффициенты хроматической аберрации А 2 = 0.47, А 3 =- 0.56.

На рис. 5 показано поведение узкого пучка ионов в призменном анализаторе с КАП и его раз-

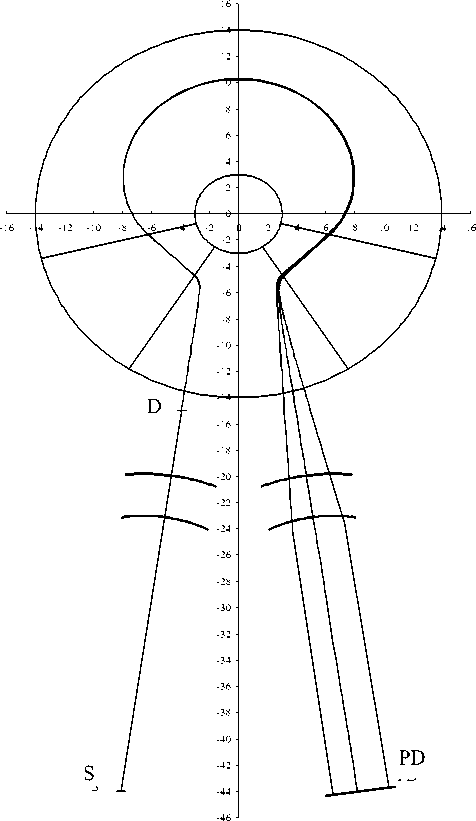
Рис. 5. Разделение параллельного узкого пучка ионов по массам в КАП для двух масс с относительной разницей в массах у = ± 0.002.

Здесь S — источник ионов, D — диафрагма, PD — позиционный детектор

деление по массам. На рисунке схематически изображена КАП и показаны границы электродов коллиматорной и фокусирующей трансаксиальных линз. Значения на координатных осях приведены в единицах d .

На этом рисунке изображены осевая траектория ( y = 0) и две крайние траектории, по которым движутся ионы с относительной разницей в массах Y = ± 0.002. Визуально видно, что угловое разделение по массам нелинейно. Угловое отклонения траекторий АТ от осевой траектории в зависимости от γ хорошо описывается следующей формулой:

АТ = D' m Y + А 2 m Y ². (15)

Здесь угловая дисперсия по массе D'_m = 51.275, а коэффициент второго порядка А_m = 4995.9.

На рис. 6 показаны проекции узкого пучка ионов на горизонтальное и вертикальное направления в параксиальном приближении. Здесь S — длина пути вдоль осевой траектории, q — отклонение частиц от осевой траектории в горизонтальном направлении. Видно, что в вертикальном направлении пучок образует пять промежуточных линейных фокусов.

Проводилось интегрирование N=1000 траекторий, для которых начальные условия определялись в заданных интервалах методом Монте-Карло. Параметры пучка задавались, примерно как в масс-спектрометре Матсуда [2]. Результаты расчета приведены в Приложении на рис. П1–П3. Распределение частиц в ионном источнике показано на рис. П1. Если считать d = 1см, то ширина источника S = 100мкм (|у0|<0.005). По углам а и β предполагалось нормальное распределение в интервале "трех сигма", которое моделировалось с помощью алгоритма Метрополиса. Брались следующие значения интервалов: Zz0| < 0.05, |а| < < 0.005 (в 2 раза больше, чем у Матсуда), в < 0.002. Для сравнения: у Матсуда S = 84мкм, а = |в| < 0.0025.

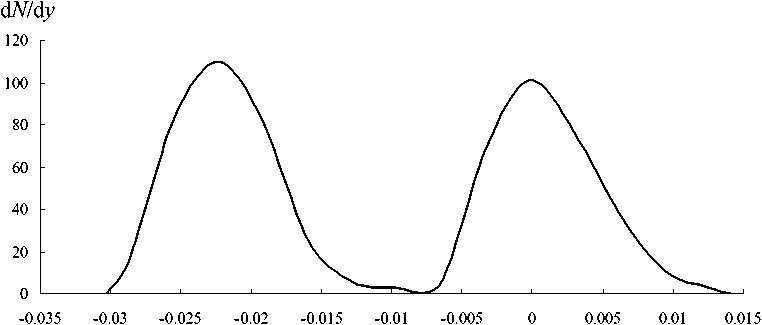
В Приложении на рис. П2 показано распределение частиц в плоскости детектора, куда из 1000 частиц долетели лишь примерно 630. Остальные частицы были задержаны диафрагмами или попали на электроды КАП. На рис. П3 показан масс-спектр для массового дуплета, половина частиц которого имела Y = 0, а половина — Y = 1/ 20000, т.е. разрешение здесь более 20000, а на полувысоте пиков разрешение около 40000.

Таким образом, по сравнению с масс-спектрометром Матсуда [2] при почти одинаковых размерах прибора и параметрах пучка мы получаем более чем в 6 раза большее разрешение. В масс-спектрометре Матсуда было получено разрешение 5000 при S = 84мкм .

q, условные ед.

а

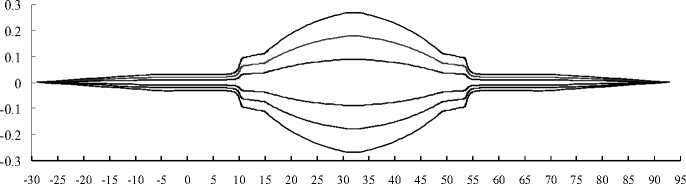
s, условные ед.

0.15

z , условные ед.

б

0.1

0.05

-0.05

-0.1

-0.15

-30 -25 -20 -15 -10 -5   0   5   10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95

• s ,    условные ед.

Рис. 6. Проекции ионного пучка на горизонтальное (а) и вертикальное (б) направления dN/dy 180 160 140 120 100

80 60 40 20

• -0.035    -0.03    -0.025    -0.02    -0.015    -0.01    -0.005      0      0.005    0.01     0.015

y , условные единицы

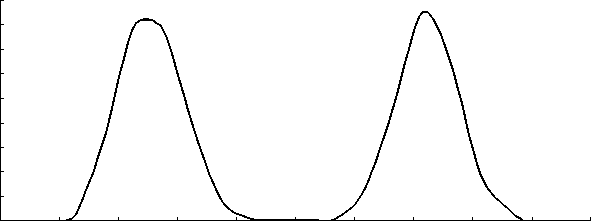
Рис. 7. Масс-спектр дуплета масс.

Левый пик соответствует у = 1 / 20000, а правый — у = 0

Наибольшие аберрации в призменном масс-анализаторе обусловлены отклонением частиц от средней плоскости. Дело в том, что идеальная вертикальная фокусировка пучка, как показано на рис. 6, осуществляется только в параксиальном приближении, которое справедливо лишь в том случае, когда отклонение пучка от средней плоскости не превосходит 0.05 d . Даже обрезая пучок двумя диафрагмами, которые расположены на входе и на выходе из КАП, мы получаем аберрации, сравнимые по величине с шириной источника.

Если использовать более узкие пучки, то можно добиться 100 % прохождения пучка через анализатор и при этом получить более высокое разрешение. Если взять следующие значения интервалов: |у0|< 0.0025, |z0| < 0.01, |а| < 0.005, в\ < < 0.0005, то получим практически 100 % прохождение частиц и масс-спектр для массового дуплета, половина частиц которого имела у = 0, а половина — у = 1/ 20000, представленный на рис. 7. Видно, что разрешение здесь более 50000 на полувысоте пиков.

ЗАКЛЮЧЕНИЕ

Отметим также, что рассчитанный масс-анализатор с КАП может быть использован и как масс-спектрограф. Действительно, компактный масс-спектрограф с высоким разрешением и чувствительностью можно осуществить, установив позиционный детектор в фокальной плоскости фокусирующей линзы. При этом можно наблюдать довольно широкий фрагмент массового спектра с высоким разрешением. Таким образом, можно создать небольшой прибор для изотопного и химического анализа с рекордными характеристиками, что позволит получать новые интересные экспериментальные результаты.

z, услов. единицы

0.06

-0.06

ПРИЛОЖЕНИЕ

а

б

0.04

0.02

-0.02

-0.04

-0.01   -0.005     0      0.005    0.01

y , услов. единицы

β , рад 0.002

-0.002

0.001

-0.001

-0.005   -0.003   -0.001    0.001    0.003    0.005

α , рад

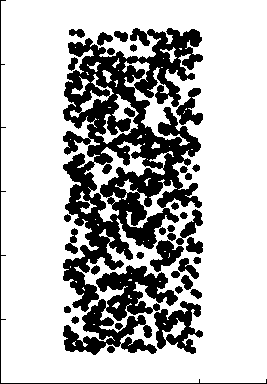
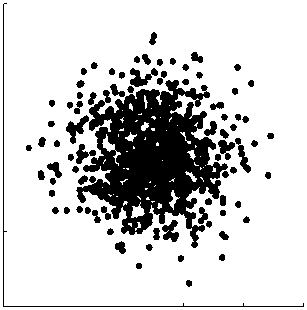
Рис. П1. Распределение частиц в ионном источнике по координатам (а) и углам вылета (б)

z, услов. ед.

0.3

0.2

0.1

-0.1

-0.2

-0.3

-0.04      -0.03      -0.02      -0.01        0        0.01       0.02

y, условные ед.

Рис. П2. Распределение частиц в плоскости детектора для двух масс с γ = 0 и γ = 1/20000

y , условные едиицы

Рис. П3. Масс-спектр дуплета масс.

Левый пик соответствует γ = 1/20000, а правый — γ = 0