Прямой алгоритм проверки изоморфизма графов

Задача изоморфизма графов (ИГ) принадлежит к задачам, относительно которых нет ясности: являются ли они полиномиально разрешимыми или нет [1], тогда, как известно, эта задача полиномиально разрешима для некоторых классов графов. В частности для планарных графов, графов с ограниченной степенью вершин, графов с ограниченной кратностью собственных значений из спектра матрицы смежности [2], [3], [4] и некоторых других классов графов построены эффективные алгоритмы решения этой задачи.

Поскольку эти алгоритмы используют специфические структурные характеристики графов, область их эффективного применения ограничена. Возникает необходимость в алгоритме, который находил бы решение задачи ИГ для как можно более широкого класса графов, оставаясь при этом полиномиальным как по времени, так и по памяти.

Алгоритм, представленный в [5], работает со спектральными характеристиками графов и является полиномиальным алгоритмом решения задачи ИГ с наиболее широким классом применения. Но этот класс не покрывает определяемых спектром графов, которые попадают в область эффективного применения предлагаемого алгоритма. Граф называется определяемым спектром (ОС-графом), если ему изоморфен любой граф с таким же спектром матрицы, представляющей граф. Спектр матрицы графа так же называют спектром графа.

Спектр графа не является его полным инвариантом. Так, почти все деревья и сильно-регулярные графы не являются определяемыми спектром. Вместе с тем, спектр содержит в себе разнообразную информацию о структуре графа [6] - такую как число ребер в графе, степенная последовательность графа, род графа и др., что может быть использовано при построении эвристик для решения задачи ИГ. Алгоритм спектрального расщепления [7], работает не напрямую со спектром графа, а со следующим, связанным со спектром, инвариантом:

удалением i -ой вершины; произведения берутся по всем значениям из спектров. Будем называть граф определяемым спектрами графа и подграфов (ОС2-графом), если ему изоморфен любой граф с таким же значением S .

Как показывает эксперимент, многие графы, которые не являются ОС-графами, например, деревья являются ОС2-графами. Тогда как всякий ОС-граф является ОС2-графом.

В задаче проверки изоморфизма графов даны два графа G A и G B с множествами вершин V ( G A ), V ( G B ) и ребер E ( G A ), E ( G B ). Мощности множеств вершин и ребер графов равны. Требуется определить, существует ли такое биективное отображение (изоморфизм) ф : V A ^ V B , что

(i, j) € E(GA) о (ф(i), Ф( j)) € E(Gb ), и представить его, если графы изоморфны.

При работе со спектром графа могут рассматриваться различные варианты матриц, представляющих граф. Все они являются некоторыми модификациями матрицы смежности графа A 0 . A - ( a_y ), где

[ 1,( i , j ) € E. , a j =L „ A [ 0, иначе,

B о = ( b j ) — матрица смежности графа G g .

Чем больше кратность собственных значений в спектрах графов, тем больше в графах симметрий, и тем более сложным является нахождение изоморфизма двух изоморфных графов с кратными собственными значениями. Предлагаемый алгоритм решения задачи проверки изоморфизма графов работает с видоизмененными матрицами смежности. В ходе его работы последовательными согласованными возмущениями диагональных элементов матрицы производится расщепление собственных значений графа, что позволяет решать задачу проверки ИГ для широкого класса графов за полиномиальное время в смысле количества используемых машинных операций.

Алгоритм является прямым, то есть решение производится без использования схемы рекурсии с возвратом, на которой основаны наиболее извест- ные алгоритмы решения задачи ИГ без каких-либо ограничений на структуру проверяемых на изоморфизм графов – алгоритмы Ullman, NAUTY и VF, экспоненциальные для общего случая задачи.

Алгоритм

Пусть A ₀   – матрица смежности графа

G A = V, , E A) , D A 0 — диагональная матрица следующего вида:

d 1   0.

0 d 2

•     •\ •

_ 0   0

n где di = ^ a” + d = di + d , d - максимальная сте-j=1

пень вершин в графе G_A , d_i – степень вершины i e V A . Матрица D B 0 строится аналогично в соответ -ствии с матрицей B ₀ . Алгоритм работает с матрицами следующего вида:

A = A + D, , B = B + D„ .                  (1)

0 A ₀^,          0 B ₀

Матрицы вида (1) – положительно определенные матрицы с диагональным преобладанием. Матрицами графов далее будем называть матрицы вида (1). В ходе работы алгоритма производится возмущение матриц графов при помощи следующих матриц:

"0 . 0 . 0"- 1 Ek = 0 . 1 0 - k _0 . 0 • 0_ - n На i -ой итерации будем производить следую- щие возмущения матриц графов:

A i : = A i ^{- 1} + e E i ,B i : = B i ^{- 1} + e E^j , где J выбирается так, что S ( G A ) = S ( GA ). Если G A и G_B – ОС2-графы, и G_A изоморфен G_B , то проведение таких возмущений возможно, поскольку имеет место очевидная лемма.

Лемма 1. Пусть G_A и G_B – изоморфные ОС2-графы, P – матрица перестановки, соответствующая изоморфизму ф : V B ^ V A . Пусть A^J и B^J -матрицы, получаемые из A и B возмущениями их диагональных элементов в соответствии с последовательностями { J } j = и { k_J } j =₁ , где ф ( k_J ) = J . Тогда

A = PBP ^{- 1} О V j A = PB^JP ^{- 1} .

Обращение матриц производится путем решения систем линейных уравнений A ‘ x = e_J , B i x = e_J , где

{ e J } j = — стандартный базис в R" . Пусть x_k = ( xk ₁, . , xkn ) - k -й вектор-столбец матрицы ( A ‘ ) ^{- 1} . Тогда если графы G A и G B изоморфны, и ф -

изоморфизм		GA на	GB , то
	" x 11   .	x 1 ,	■    x 1 j
	.	x« ••	• x j
	_ x j 1 .	x j,-	x ’      jj _

y ф(1)ф(1)     •	y ф(1)ф( i )	y ф(1)ф( j )
y ф( , )ф(1)	y ф( i )ф( , )	y ф( i )ф( j )
y ф( j )ф(1)	y ф( j )ф( i )	y ф( j )ф( j )

Пусть j-1         / j

\ k/П*

k =1      / k =1

а R ( A ) = { Л . , . , л ,. } - это набор неповторяющихся значений Л i для матрицы A . Если | R ( A ) | = j , то есть если все диагональные элементы обратной матрицы к матрице A графа – разные, и G_A и G_B изоморфны, то, очевидно, изоморфизм может быть установлен без проведения возмущений по следующему правилу:

i = Ф( J)О л, = Лj.

Докажем следующую лемму.

Лемма 2. Пусть A' = A + е E‘ , A'x i = e i , Л , = xV . Тогда может быть выбрано такое е , что Л i ^ Л _j для любого J * i .

Доказательство. Пусть A_pq – алгебраическое дополнение элемента a_pq матрицы A .

A x» =----- ii det A

.

Поскольку элемент aii матрицы A – единственный изменяемый в ходе возмущения матрицы элемент, то A’i = Aii, тогда как для любого J * i получаем A'A = AJJ + еAi; JJ, где Aii A - определитель подматрицы матрицы A , получаемой удалением ее i -ой строки, i -го столбца, j -ой строки и j -го столбца. Изменение определителя при возмущении следующее: det A' = det A + eAu. Получаем, что при надлежащем выборе е для любого J * i л j = Ajj+sAjj• ii #----Ai— = л i.

j   det A + s A ii   det A + s A ii

Лемма доказана.

Учитывая леммы 1 и 2, можно утверждать, что не более чем за n последовательных согласованных возмущений матриц изоморфных ОС2-графов мы можем добиться того, что

|R(An0)|=|R(Bn0)|= n, где n0 - необходимое число возмущений, n0 < n .

Принципиальная схема алгоритма

Шаг 0. i : = 1, A ⁰ : = A , B ⁰ : = B .

Шаг 1. Если | R ( A i ^{- 1} ) | = n , то перейти на шаг 3, иначе перейти на шаг 2.1.

i -я итерация алгоритма:

Шаг 2.0. Выбор s .

Шаг2.1. A i : = A i ^{- 1} + s E i .

Шаг 2.2. Поиск j т. ч.

S ( G A i ) = S ( G B i - 1 +s E j ).

Шаг 2.3. Если j не найден, то, либо поданные на вход графы не изоморфны, либо – не являются ОС2-графами. Работу алгоритма завершить, иначе перейти на следующий шаг.

Шаг 2.4. i : = i + 1. Перейти на шаг 1.

Шаг 3. Установить изоморфизм по правилу

i = ф( j) о Лi = Лj.

Вычислительная эффективность алгоритмаЛокализация элементов множества R

Пусть R ( A ⁽ j ) ) = { л ⁽ j ),..., Л ^ ) } - набор R к j -ой итерации. Обозначим решение системы уравнений A^jx = e k , как x k ^j ) , и определим множества R i ( A ^{( j} ) ) как

R i ⁽ A j ) = { ^{x j} | x j = ^{л j} } , i = ¹ P .

Рассмотрим множества Ri (Aj ) в процессе производимых в ходе работы алгоритма возмущений матрицы A . Будем говорить, что Ri (Aj-1) расщепляется на j -ой итерации алгоритма, если xj-1) e R(Aj-1) , | Ri(Aj-1)|> 1

для некоторого i , но xj) e Rk(Aj), и |R(Aj)|= 1.

Положим,

( j )           ( j )         ( j )

Aki = |xk,k, -xi I, где xk e Rk(A) xj e Ri(A >■ xj e Ri(Aj)- Будем рассматривать Aj как расстояние между множествами Rk(Aj) и Rl(Aj).

Числом обусловленности матрицы A называется следующая величина ц ( A ):

ц( A) = sup x #0,5#0

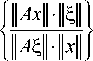
где ||-|| - евклидова норма вектора в Rⁿ . Пусть X _max -наибольшее собственное значение матрицы A , X mi- - наименьшее.

sup) | A^x||/||^x|| _х

^ ( A ) =     --- = -max- < ” .

sup| |A §/§    Xmin

^#0

X _min # 0 , поскольку A - положительно определенная матрица.

Рассмотрим систему ( A + C ) y = f , полученную из системы Ax = f возмущением A при помощи матрицы C . Пусть

Н<6, где A=sxUP Tx*.

II A ll = ^_max для положительно определенной матрицы A [8]. Имеет место следующая теорема [8].

Теорема 1. Если 9ц ( A ) <  1, то

IIУ - xll < 6Ц(A)

|| x||       1 -6Ц ( A ).

Для числа обусловленности симметричной матрицы выполняется [8]:

Ц ( a ) S^ A , Х ( A ) где

n ( A ) = max i a_H + ^ | a j | I , 1< <  n

V       j # i7

x(A) = min I aii-£ | aij | I. 1< I < n

V      j # i7

На j -ой итерации a_kk = d + d_k + s _k , где s _k - значение возмущения k -го диагонального элемента A , и s _k = 0 если k <  j . Пусть i - номер строки, на которой достигается n ( A ), i ₂ - номер строки, на которой достигается х ( A ). Имеем

n

n ( A ) = a,, + £,■ + У| a, , | = d + е, + d, +

IV /         Zj Zj         Zj      ^1    Zj j I                Zj         Zj j=’

+d, = d + £ + d + d = 3d + £, , zj                                 zj                                                                     zj

Имеем

X ц ( A^j -1 ) = ^m- <  4, x„ min

X ⁽ A ) = ^a ₄₄ ^{+ £} ₄ ■ У ^{1 a} 2 j ^| = j =’

= d + £, + d, - d, = d + £, . 12           Z2           Z2

Следовательно,

) 3 d + £, ц( A) ■•■■'’ ’ =

X ( A ) d + s^

Если £. = jn p , e^ = ’/ n p² , где p , , p ₂ e N , то

,    , ^{3 d + £} _il 3 d + V n p

ц(A) <------L =-----

• d + £.      d + j/ n p ²

3dnp + ’ < np2-4dn = 4 dnp2 +’            dnp2’

Таким образом, в нашем случае утверждение теоремы ’ принимает следующий вид:

Если 9 < ’4, то где Xm„„ - максимальное собственное значение max

A j -’ , X _min — минимальное. По теореме Гершгорина

• [9] X _max >  d . Учитывая, что X _min <  I A j -’ll , получаем

I A^j -’|| >X m„ >X max/4 >  d /4.

Таким образом, из (3) следует

I x :^j)- x    d^ -I

Так как все собственные значения A ^j не меньше ’, и || e_k 11 = ’ для любого к , то || x _Z⁽j ^-’⁾ 1| <  ’. Из (3) следует, что для любого Z

x ( ^j

dnp

y-1

.( j -j)

i

„ ( j ) x_ii

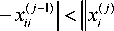
следовательно, для любого Z

II у - x < ⁹। ⁴ _{4 9}1 * И "

„ ( j ) ^xii

_ _Y ( j -j) ^xii

dnp

Для гарантированного выделения x jj ^j) из

R_Z ( A j ^- ’ ) на j -ой итерации возмущения должны быть достаточно малы, поскольку необходимо, чтобы после возмущения x j был достаточно удален от всех остальных значений x (j ) в смысле введенного расстояния А .

Из (2) следует, что

Неравенство (4) дает оценку локализации векторов из множеств R_Z .( A^j ) в процессе работы алгоритма.

I x U) - x(j -’) I|<

I ‘       ‘ H ’ - 4 9 ( £ j )

II x j -I-

Поскольку

_H_j ■ I A j -'ll    II A^{j -j}     II A j -T

мы можем положить

£ _j

^{9 ( £ j )} = j ^-

Полагая £ j

, получаем

x^j ) - x^{j - j)}

⁴ n p _____ll x ( j -»|| =

11 - 4/ n^p^‘    H

4 n p ___ll x =

'll - 4/ n^p H ^Z H

=     4

= | | A^j||n^p - 4

Ajnp

Расщепление множеств R_i

Производимые возмущения должны быть достаточны для расщепления множеств R_Z . Алгоритм является вычислительно эффективным только в том случае, если для любого j и любых к и l , не равных друг другу, A ^j ) будет отличным от нуля машинным числом. Покажем, что необходимая точность решения систем линейных уравнений может быть обеспечена при помощи машинных чисел с длиной мантиссы, не превышающей n .

Пусть x ’ j ^- ’⁾ , x j ^- ’⁾ e R _Z .( A j -’ ) для некоторого i , то есть перед j -ой итерацией в этом множестве имеется по меньшей мере два элемента, препятствующих установлению взаимнооднозначного соответствия между вершинами графов.

Теорема 2. Если x^{( j)} = x j ^j) и 0 < £ j <  ’, то

- (j) _ x (j) I >_____________’_____________ jj 1 3 nd 2(3 d I £j+ ’)

.

Доказательство. Пусть A = A^{j -} ’ , A ' = A^j, x. = x < j -^j) , x ’ = x < j ) , x j = x jj -^j) , x j = x jj ) . Если x 'j- = Px' j , то x ' j = x j .

x' = A jj x' = A*

j¹ det A* ’" det A* "

После возмущения det A' = det A + s jAjj, Ajj = Ajj, так как ajj – единственный изменяемый элемент A на итерации алгоритма. Поскольку

Aj = A,, +s A, ^, и A. = Ajj, так как xi = xjj, получаем

| x j - x ^j | =

A j j	A i.
det A	det A'

Ajj - An +sjAii,j =    sjAii,jj det A'     det A'      det A + sjAjj '

A_{ii , jj} – определитель подматрицы A , получаемой удалением из нее i -х строки и столбца и j -х строки и столбца. A – симметричная положительно определенная матрица с диагональным преобладанием, для которой выполняются условия Адамара:

Hk H akk | -Z1 aki 1 = dk > °, i =1, n, l * k

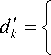
где d + s k, если 1 < k < j, d, если 1 < k < j.

Следовательно,

черта сверху означает невключение в произведение.

С другой стороны, по теореме Гершгорина максимальное собственное значение X max матрицы A можно оценить так:

x   < 3d + maxs. < 3d +1, max

1< k < j если sk < 1 для любого k . Поэтому

n det A = ПХk

k=1

n-1

Ajj = №kn  < (3d +1)n^-1.                (8)

k=1

Пусть X’ - максимальное собственное значе-max ние подматрицы, получаемой из A удалением строк и столбцов с номерами i и j. Xmax

x - x ' l=       ^j..•^jj_____

" jj det A + sjAjj

>

>

s dⁿ-2

>

(3 d +1) n + sj (3 d +1) n^-1

sjdn^-2

(3 d)ⁿ⁺¹+ sj (3 d) n’

то есть

x⁽j) - x (Ij) >.

¹ jj ¹3 nd 2(3 d / sj +1)

Теорема доказана.

Пусть решение систем линейных уравнений A^jx = e_k и B^j x = e_k (j, k = 1, n) осуществляется методом Гаусса-Зейделя. Метод Гаусса-Зейделя позволяет оценить необходимую длину мантиссы используемых машинных чисел. В действительности не принципиально, каким методом мы решаем системы уравнений, необходимо только, чтобы решение находилось с нужной точностью за приемлемое время.

Имеет место [10] следующая теорема.

Теорема 3.Пусть

ZI aj l< YI a.il, Y < 1, j * i для каждого i = 1, n . Тогда

IIx - x$ll

Если A = A^j, то y< 1/2 . Следовательно, на s -ой итерации метода Гаусса-Зейделя

| xii^-xts | <|xi^-xts||< 2- 8°,

I xjj- x ^|<| xj- -xsll < 21Г 8°, где 8° - ошибка начального приближения. Если sj = Vnp на j -ой итерации, то, учитывая (9), полу- чаем

I x (j) - x (j) I >____________¹____________

। ^jj             3 nd²(3 dnp +1)

Значит, если

10                1

—г 8 < ——2-------,

2^s-1       3 nd 2(3 dnp +1)

.

то разница x j - x*⁷) может быть зафиксирована машинными числами с длиной мантиссы, не превышающей n . Оценим количество итераций метода

Гаусса-Зейделя s , необходимых для фиксирования этого значения.

Формула (10) эквивалентна

3nd2(3dn^p +1)80 < 2s^-1.                           (11)

Логарифмируя (11), получаем n log2 3 + log2 d2(3dnp +1) + log2 80 < s -1, то есть число необходимых итераций метода Гаусса-

Зейделя может быть оценено как s > n log2 3 + p log2 n + 3 log2 d + log2 80 + 3 . (12)

Пусть p > 0 определяет значение возмущения ej = 1)n^p . Пусть x(j^-1)- значение, выделяемое из Ri(Aj^-1) на j -ой итерации. Выберем p так, что

20 А

. р <    , dn p n то есть

Р >^logn "77 + 1, d А

Общая вычислительная сложность алгоритма

На каждой итерации алгоритма мы проводим вычисление наборов R для обоих графов, для чего мы обращаем матрицы графов. Для обращения матриц необходимо решить 2n систем линейных уравнений. Пусть O(N_X ) – число элементарных машинных операций, которые необходимо совершить для решения систем линейных уравнений с заданной точностью. Тогда сложность процедуры обращения матриц составит 2n ■ O(N_X).

Проверка равенства значений из R(A) и R(B) (проверка равенства значений S(A) и S(B)) для пары матриц A и B осуществима за O(n) элементарных машинных операций. Следовательно, общая сложность одной итерации алгоритма составляет

2 n ■ O (N_X) + O (n). (13)

Оценим O(NX ) для метода Гаусса-Зейделя. На j -ой итерации алгоритма, находя ej, мы вычисляем p такое, что 20/dnp <Аj]n , где Аj = min А^), то есть где А = min АЧ).

k i l ^kl

Из (4) следует, что для любого i

Р = log n + 1. d А j

хУ-1)

-

х»'| < /0-  '

dn p n

Получаем

< lx⁽j) - x(j) <

3 nd 2(3 d / ej +1) ¹ " ^{jj 1} n

После чего, в соответствии с (12), выполняется s итераций метода Гаусса-Зейделя. Пусть N_X^j – сложность нахождения решений систем линейных уравнений на j -ой итерации алгоритма проверки изоморфизма графов. Тогда, с учетом (13),

после j -ой итерации. Это означает, что на j -ой итерации мы можем выбрать такое возмущение, которое давало бы выделение xj^-1)из содержащего его множества Ri (A^j-1) (если его мощность не равна 1), фиксируемое при помощи машинных чисел с длиной мантиссы равной n при сохранении локализации значений xi, i = 1, n . То есть могут быть заданы интервалы, в пределах которых будут происходить расщепления множеств R_i . Возмущения могут проведены таким образом, что после выделения x_jj из некоторого Ri (A^j-1), xj не попадает на следующей итерации в другое такое множество с мощностью отличной от 1.

В результате, если для решения систем линейных уравнений производится число итераций метода Гаусса-Зейделя, определяемое (12), то при n₀< n мы получаем | R(An⁰) |= n , и расщепление элементов из R фиксируется машинными числами с длиной мантиссы, не превышающей n .

j_Ti            2x                               1

N^J_X = O(n ) ■( n log₂3 + log_n — +1 log₂n +

А, J

+3 log2 d + log2 8 + 3), поскольку одна итерация метода Гаусса-Зейделя требует O(n2) элементарных машинных операций. Точные решения систем линейных уравнений принадлежат отрезку [0,1]n e Rn, следовательно, мы можем положить 80 = O(Vn). С учетом (13) общая вычислительная сложность алгоритма может быть оценена как

f Г 2 .          1

O n х max nn + log„—log₂n + log₂n

1< j< n                  а -

1< j< n

= O (n⁴).

л

Заключение

В класс ОС2-графов, для которых алгоритм решает задачу проверки изоморфизма графов, как и в класс ОС-графов, не попадают известные серии сильно-регулярных графов и некоторые другие, традиционно сложные для решения задачи ИГ графы.

Но, как показывает вычислительный эксперимент, в класс ОС2-графов попадают не только ОС-графы, но и многие графы, таковыми не являющиеся. Так, в библиотеке тестовых задач [11], использовавшейся для сравнения алгоритмов решения задачи ИГ на основе рекурсии с возвратом, не найдено примеров неправильного решения задачи ИГ представляемым алгоритмом для деревьев, случайных, планарных графов, регулярных n -мерных сеток (n ≤ 4) и некоторых других. Установлено также, что алгоритм решает и те задачи ИГ из этой библиотеки, на которых время работы алгоритмов Ullman и NAUTY становится экспоненциальным.

Несмотря на то, что в обосновании алгоритма длина мантиссы предполагается равной n , при проведении вычислительных экспериментов достаточным было использование числового типа extended, реализованного в языках Object Pascal и С++, позволяющего работать с машинными числами в диапазоне от 3,6×10^-4951 до 1,1×10⁴⁹³².