Прямой способ расчета параметров соединений типа "звезда" методом виртуальных компонентов

В настоящее время алгоритм расчета токов в ветвях соединений типа «звезда» (рис.1) традиционными способами, предусматривает последовательное выполнение ряда таких процедур как эквивалентные подстановки, преобразования и/или методы линейной алгебры [1,с.34; 2].

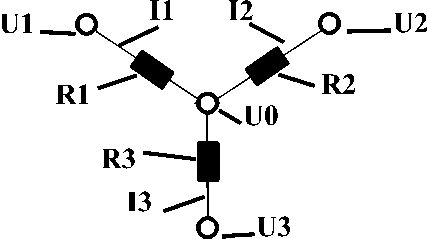
Рисунок 1.

R1, R2, R3 – сопротивления ветвей соединения, Ом;

I1, I2, I3 – токи ветвей, Ампер; U0 – напряжение общей точки, Вольт;

U1, U2, U3 – напряжения узлов относительно общего нуля, Вольт.

Для наглядного представления логики вывода уравнений прямого рас чета токов, схема (рис.1) для узла U3, приведена к следующему виду:

Рисунок 2.

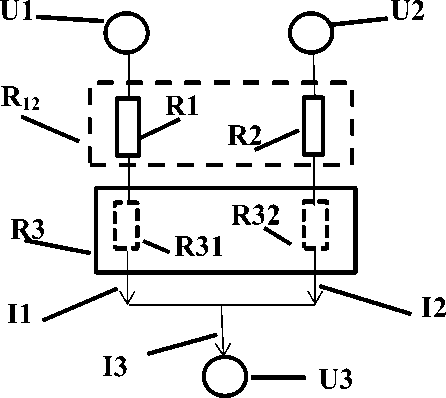
Штриховой линией показаны виртуальные компоненты.

При таком изображении (рис.2) сформированы две виртуально независимые цепи: U3-U1, R1+R31; U3-U2, R2+R32. Резистор R12 рассчитывается по формуле для виртуального параллельного соединения резисторов R1 и R2.

Поскольку, согласно следствию закона токов Кирхгофа, ток одинаков для всех последовательно включенных элементов цепи [1,с.27], то соотношение токов I1 и I2 постоянно для вышеприведенной схемы (рис.2). Также сохраняется соотношение виртуальных пассивных компонентов в R12 и R3 обоих цепей, которые задают ток. Следовательно, соотношения между виртуальными резисторами R31 и R32 между собой и реальным резистором R3 повторяют соотношения между R1, R2 и R12, которые можно записать в следующем виде:

R31/R3 = R1/R12 и R32/R3 = R2/R12.

Разворачивая каждое из равенств, получаем следующие выражения: R31 = R3*R1/R12 = R3*R1(R1+R2)/R1*R2 = R3*(1+R1/R2);

R32 = R3*R2/R12 = R3*R2(R1+R2)/R1*R2 = R3*(1+R2/R1); то есть:

R31=R3*(1+R1/R2)  и  R32=R3*(1+R2/R1).

Проверка:

R3 =

R3∗

(R2+R1) R2

∗R3∗

(R2+R1) R1

(R2+R1)      (R2+R1)

R3∗      +R3∗

R2          R1

R3²∗(R2+R1)² R3∗(R2+R1)

1 ∗R1

^R— = R3*(R2+R1)

R2 + R1

1⁄R2∗R1

*   R2+R1

R2∗R1

=R3

Аналогичным способом находятся выражения виртуальных компонентов для остальных узлов.

Относительно U1 :   R12 = R1*(1+R2/R3); R13 = R1*(1+R3/R2)

Относительно U2 :   R21 = R2*(1+R1/R3); R23 = R2*(1+R3/R1)

Токи для ветвей вышеприведенной схемы (рис.1) рассчитываются по формулам:

11 = 12 +13 ;  12 = 11 + 12 ;  13 = 11 + 12.

В развернутом виде:

I1 = (U1-U2)/(R2+R1*(1+R2/R3)) + (U1-U3)/(R3+R1*(1+R3/R2))

I2 = (U2-U1)/(R1+R2*(1+R1/R3)) + (U2-U3)/(R3+R2*(1+R3/R1)) к {1}

I3 = (U3-U1)/(R1+R3*(1+R1/R2)) + (U3-U2)/(R2+R3*(1+R2/R1))

Потенциал общей точки рассчитывается также независимо относи тельно любого узла соединения:

R1*R2

R1*R2 + R1*R3+R2*R3

R1 * R3 U0-U1- (U1 - U2) *                     - (U1 -

R1 * R2 + R1 * R3 + R2 * R3

R2*R3                        R1*R2

^U0 - ^U 2 - ^(U 2 - ^U1) * ——    —    —— ^{- (U} 2 - ^U3) * ——    —    ——

R1 * R2 + R1 * R3 + R2 * R3             R1 * R2 + R1 * R3 + R2 * R3

R2*R3                        R1*R3

^U0 = ^U 3 ^{- (U} 3 ^{- U1)} * ——    —    —— ^{- (U} 3 ^{- U2)} * ——    —    ——

R1 * R2 + R1 * R3 + R2 * R3             R1 * R2 + R1 * R3 + R2 * R3

Разности напряжений определяются относительно центральной точки узла.

Ток каждого данного узла есть алгебраическая сумма токов прилегающих ветвей.

Правильность расчетов проверена по контрольным замерам на макетах практических схем. Совпадение параметров полное во всех точках.

Предложенная методика позволяет упростить процедуры расчета токов в соединениях типа «звезда» (рис. 1) и позволяет отказаться от применения метода эквивалентных и прочих преобразований для расчета указанных выше параметров.

Развернутый анализ системы уравнений {1} выходит за рамки заявленной темы публикации поэтому будет представлен отдельно.