Прямолинейное равномерное течение газов с теплоотдачей в энергетических установках летательных аппаратов

При проектировании энергетических установок летательных аппаратов необходимо учитывать большое число факторов, влияющих на надежность и энергоэффективность изделия. Одним из таких факторов являются тепловые потоки, образующиеся в результате теплоотдачи и трения газового потока при течении в газовых магистралях энергоустановок. Неучтенное в расчете тепло при проектировании узлов и агрегатов влияет на теплофизические свойства рабочего тела, такие как плотность и вязкость. В некоторых случаях при значительном градиенте температур возможно появление пластических деформаций в элементах конструкции. Нерасчетные величины вязкости и плотности рабочего тела могут вывести рабочие параметры за предел расчетного объема работы установки, который для получения максимального КПД имеет довольно узкий диапазон величин.

При учете влияния тепловых потоков и теплоотдачи в настоящее время пользуются либо полуэмпири-ческими зависимостями, либо численными методами, реализованными в различных пакетах прикладных программ. Полуэмпирические и эмпирические зависимости для учета теплоотдачи основываются на обобщении экспериментальных исследований и не всегда могут применяться для решения широкого круга задач. Использование современных пакетов прикладных программ расширяют возможности теплового расчета, однако должно сопровождаться сложными теплофизическими экспериментами для верификации результатов численного моделирования.

y

A

x

u

5t

⁵ U

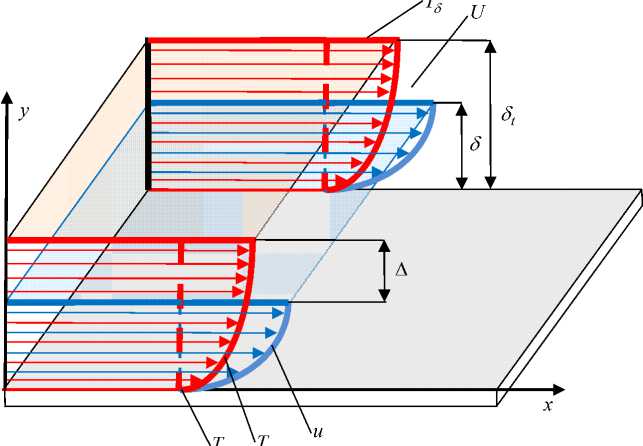
Рис. 1. Распределение температурного и динамического пограничных слоев при турбулентном течении газового потока

Для достоверного определения распределения температурных полей в проточных и вспомогательных полостях течения рабочего тела в тепловом расчете двигателя необходимо использовать локальный коэффициент теплоотдачи. В отличие от среднеинтегрального коэффициента теплоотдачи, который дает усредненные данные по длине исследуемого участка, локальный коэффициент теплоотдачи позволяет выявить возможные местные зоны перегрева рабочего тела. Учет локальных тепловых нагрузок очень важен для таких полостей как полость между ротором и статором турбины турбонасосного агрегата (ТНА), подводящее и отводящее устройство газовой турбины ТНА.

При проведении аналитического исследования прямолинейного турбулентного течения газа или газовой смеси необходимо рассмотреть модель распределения температурного и динамического пограничных слоев при обтекании газовым потоком плоской, прямой, не проницаемой пластины (рис. 1). Толщина температурного пограничного слоя выше толщины динамического. Такое распределение толщин в некоторой степени характеризуется теплофизическими свойствами рабочего тела, а именно: у газов и газовых смесей динамическая вязкость не может быть больше температуропроводности, а их отношение всегда будет меньше единицы. В свою очередь, основное изменение скорости ( u ) от поверхности обтекаемого тела, где она равна нолю, до скорости в ядре потока ( U ), происходит в толщине динамического пограничного слоя (δ). Аналогично, основное изменение температуры (T) от температуры на поверхности теплообмена (T 0 ) до температуры в ядре потока (T_δ), происходит в толщине температурного пограничного слоя (δ t ). То-

Данное выражение характеризует величину, в которой происходит потеря энергии вследствие уменьшения скорости и температуры в пограничных слоях по отношению к скорости и температуре в ядре потока. Отношение скоростей в выражении (1) характеризует распределение профиля скорости в динамическом пограничном слое, а отношение разности температур – распределение профиля температуры в температурном пограничном слое. При различных толщинах пограничных слоев необходимо разбить границы интегрирования выражения (1). Тогда выражение для определения толщины потери энергии преобразуется

к виду

** u

⁵ 1 ф=Ь7

+

5 1 u

I и ■

гда выражение для определения толщины потери

энергии примет следующий вид:

5 t

** u I .

5 tф = I Ш

о V

^^^^^^»

T-T

TT

T — T I

T 5 T O )

dy .

T — T

T___T o

T —T 1

T 5 T O )

dy +

T-T

T___T o

т -T 1

T 5 T O )

dy .

Первый член выражения (2) отмечает изменение температуры и скорости в пределах от поверхности тела до толщины динамического пограничного слоя, второй член также, фиксирует изменение температуры и скорости в пределах от толщины динамического до толщины температурного пограничных слоев. Очевидно, что во втором члене выражения (2) изме-

нения скорости нет, т. е.:

u u = U или — = 1.

U

Тогда выражение для определения толщины потери энергии (2), в соответствие с выражением (3), запишется в виде

1 -

J0 U V

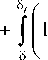
T-T

T___T o

T -T ¹

T 5 T O )

T - T 0

T 5 - T o

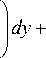
dy .

Обозначим второй член выражения (4) через 5 *

и проинтегрируем его в границах температурного по-

граничного слоя:

5 * = f

Т-Т

T TO

Т -Т I

T5 T O J

dy .

где 5 ₁ - расстояние, на котором температурное ядро

течения оттесняется наружу вследствие падения температуры в температурном пограничном слое.

Для аппроксимирования изменения профиля скорости [1], применяем «закон 1/7» степени. По аналогии с [2], используем отношение динамического и температурного пограничных слоев и обозначаем его через ^А :

.

Тогда выражение для определения толщины потери энергии преобразуется к виду

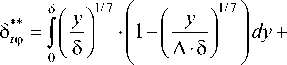
После вычисления интегралов получаем зависимость толщины потери энергии от толщины динамического пограничного слоя и безразмерного коэффициента, описывающего отношение толщины температурного к динамическому пограничному слою:

„ С7

5-1 9-А +

5** _ VА tФ -72

_

Выразим закон теплоотдачи чрез локальный коэффициент в виде критерия Стантона:

St _        q °        _                  _ p-Cp-U-(T8-To) P-Cp-U-(Tp —T°)        (9)

X p - Cp - U

d d y

T — T °

. T ₅- T °

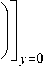
Решив выражение (9), видим, что необходимо взять производную на поверхности теплообмена от функции распределения температуры в температурном пограничном слое. Для того что бы определить производную, необходимо воспользоваться другой

моделью распределения параметров в пограничном слое. По аналогии с [4] используем двухслойную модель с ламинарным подслоем, для которой производная для выражения (9) запишется в виде выражения

d f T — T °         U ^f a^ -v) ⁴

¥ 'I T > — T ° J y _ ° a -v \V U J

U 3/4

a l ^3/2 -А ^1/4 -5 ^1/4 -v ^3/4’

где al - коэффициент ламинарного подслоя, полученный в работе [3]; здесь al _ 12,559.                     (11)

Выразив толщину динамического пограничного слоя из выражения (8) через толщину потери энергии и подставив в выражение (10), получим:

d f T — T ₀ ^

^d У 'I ^T 5 — ^T o J y _ °

0,343 - U ^3/4

1/4 3/2 3/4

а   -a 1    - v -

1/4 .

**

9-А +    — 9

А ^1/7      J

С учетом выражения (12), перепишем закон теплоотдачи в виде критерия Стантона:

St _

X -----X

X

p- Cp - U 0,343 - U ^3/4

А ^1/4 -a l ^3/2 -v ^3/4

-

1/4 .

**

⁵ 1 ф

I 7 ~

^{9 -А+} A*⁷⁷ - ⁹

А J

Подставив выражение (13) в интегральное соотношение уравнения энергии, записанное в естественной криволинейной системе координат [4], получим интегральное соотношение уравнения энергии пространственного пограничного слоя для случая течения газа или газовой смеси, когда критерий Прандтля меньше единицы:

u    d ,** 1 ^d ( ⁵ * C )

5/_m ++ h ф дф t ^ф h c de

1      d H_v, 1      d H,,

+---- ^{1 C}-5**+---- ^{1 ф}-5'

H ф - H у дф    t ^ф H ф - H у ду ¹

0,343 -X-

^{9 -А +} А 1/7 - 9

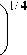
1/4 1/4 3/2 3/4 **1/4

Cp -p-А - U -a 1 -v   -5₁ ф

^фо^^^+^^Ь p- Cp - ( T 5 — T ° ) .

**

¹1 у ^_

Принимая относительную характерную толщину:

**

1 5 t y

J с X** ,

^{5 5} 1 ф

где 5 - тангенс угла скоса донных линий тока по от

**

ношению к потенциальному течению, 5 _{1 ф} - толщина

**

потери энергии в продольном направлении, 5 _{1 у} -толщина потери энергии в поперечном направлении. Переписав выражение (14), получим

1 d ... J д(5*v's) ---5/m +----+ hф дф tф hv   dv

St — 0,40662 ■

1 9 A 8 ^/7 - 9 A^1/7 + 7 1 f Pr ⁴ ■ Re ■A^8/7a l⁶ )

1    d H v    , j   д H _ф _

+----5, +----5, ■ £ —

H , ■ H v дф t ^Ф H V H v ^d V t ^Ф

Причем для расчета локального коэффициента теплоотдачи необходимо найти отношение толщин

1/4

0,343 ■X■l 9 ^A + -4 - 9 I I        A¹ / ⁷      )

1/4 1/4 3/2 3/4 **1/4

Cp ■ p ■ A ■ U ■a l ■ v ■ 5 t ф тфо ^ + £2)

p. Cp ■ ( T 5- T_o у

температурного и динамического пограничных слоев, [3] используя приближенное выражение:

A— V^

³ Pr

.

Выражение (21) с учетом формулы (22) примет

вид

При прямолинейном течении, поперечное течение д „ отсутствует, т. е. — — 0, а так же для случая прямо- dv

St — 0,40662

7 ■ Pr ⁰ , ²⁵⁸ - 9 ■ Pr ⁰ , ³³³ + 9

Pr ⁴ ■ Re ^a l⁶

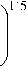
линейного течения коэффициенты Ламе определяют-dнv     днф ся Hv — 1, нф — 1, тогда —^ — 0, —— 0. Для дф      dv

Для подтверждения методики получения локального коэффициента теплоотдачи в виде критерия Стантона воспользуемся аналогией Рейнольдса о процессах переноса тепла и импульсов, применяя выражение [5]:

проведения дальнейших итераций необходимо пренебречь диссипативным членом в выражении (16),

St — 2 Cf .                  (24)

тогда интегральное соотношение уравнения энергии

преобразуется к виду

^д я** _ дф ⁵ t ^{ф —}

1/4

!■ 9 ‘A +    - 9

I A^1/7     )

1/4 1/4 3/2 3/4 **1/4 .

Cp ■p^A ■ U   ■a l    ■v   -5 _{t ф}

В интегральном соотношении уравнения энергии для прямолинейного равномерного течения (17) разделим переменные и проинтегрируем от нуля до текущего значения переменных, и определим толщину потери энергии:

**

⁵ t ф

**1/4 **

J ⁵ t ф   d ⁵ t ф ^—

(             7

0,343 •X'l 9 ■A +

(       A1/7

1/4

1/4 1/4 3/2 3/4

Cp ■ p ■ A ■ U   ■a _l   ■ v

ф

J d ф .

После интегрирования получим:

**

⁵ 1 ф

1/5

1,195 ■X⁴ / ⁵ ■f 9 ■A + A /y — 9 ) ■ф⁴ / ⁵

4/5 4/5 1/5 1/5 5/6 3/5

Cp ■p ■ U ■A   ■a 1   -v

Окончательное выражение для определения тол-

щины потери энергии необходимо подставить в вы-

ражение для вычисления локального коэффициента теплоотдачи (13):

1/5

0,956 ■X⁴ / ³ ■! 9 ^A + -У- - 9 I

_________________ f       A^1/7    )

4/5 1/5 4/5 6/5 1/5 3/5 1/5 .

Cp ■ U ■p   ■a 1    ■A ■v ■ф

Чтобы выражение привести к более простому виду, умножим числитель и знаменатель выражения (20) на динамическую вязкость ( ц ^4/5), а также воспользу-

Во всех теоретических функциях прослеживается увеличение отношения безразмерного коэффициента теплоотдачи по отношению к коэффициенту трения с уменьшение критерия Прандтля. По всей видимости, такое поведение функций обусловлено теплофизическими свойствами рабочего тела. С уменьшением числа Прандтля у рабочего тела увеличивается теплопроводность, что приводит к увеличению коэффициента теплоотдачи и уменьшению вязкости, что, в свою очередь, приводит к уменьшению коэффициента трения (рис. 2).

На графике видно, что только при Pr — 1 сохраняется равенство St — 1 Cf. В диапазоне Pr — 0,7...1, что характерно для реальных газов и газовых смесей, среднее расхождение с теориями других авторов составляет не более 10 %. Стоит отметить, что сравнивать теории в области малых чисел Прандтля невозможно, так как зависимости, полученные различными авторами, предназначены для рабочих тел с числом Прандтля не намного отличным от единицы.

Таким образом, опираясь на удовлетворительный результат сравнительного анализа, можно сделать вывод о том, что с учетом принятых допущений исходное интегральное соотношение уравнения энергии пространственного пограничного слоя, позволяющее рассматривать различные течения газового потока, может быть использовано для вывода локального коэффициента теплоотдачи при реализации вращательных течений газа в полостях турбоагрегатов.

емся безразмерным критерием подобия Рейнольдса:

p^ u ■ф!             „              н^ Cp I

Re —------ и критерием Прандтля: Pr —---- ,

( Н )                          f X )