Проблема генерирования псевдослучайных последовательностей составных распределений для имитации СМО

Универсальная среда дискретно-событийного моделирования GPSS WORLD широко используется при моделировании систем массового обслуживания, а также при моделировании производственных систем [1–4]. Она включает множество библиотечных программ, в том числе генераторы псевдослучайных последовательностей для различных законов распределений. В то же время в этой системе отсутствуют генераторы гиперэкспоненциальных и гиперэрланговских распределений. Этот факт препятствует моделированию систем массового обслуживания G/G/1 и G/G/m. Настоящая статья посвящена частичному устранению этого пробела.

Как известно, например из [3], гиперэрлан-говский закон распределения представляет собой вероятностную смесь нормированных распределений Эрланга. К примеру, функция плотности гиперэрланговского закона второго порядка имеет вид f (t) = 4 p Х2 te " t + 4 (1 - p )X2 te2' t (1) и обеспечивает коэффициент вариации c e (1 / V2, да).

Также известно, что обычно используется распределение Эрланга второго порядка как частный случай более общего гамма-закона распределения:

f ( t ) = * ² te^-x t .                    (2)

Генератор гамма-распределения GAMMA (Stream, Locate, Scale, Shape) позволяет получить псевдослучайную последовательность для распределения Эрланга второго порядка (2). Распределение (2) отличается от нормированного распределения f ( t ) = 4 X ² te^^2X t числовыми характеристиками, кроме коэффициента вариации. В связи с тем, что нормированное распределение вызывает сложности генерации, сформируем из

• (2)    новый гиперэрланговский закон второго порядка (HE₂) с функцией плотности

a ( t ) = p 2 2 te^-x ' ¹ + (1 - p ) 2 2 te^-x 2 ¹ (3) как вероятностную смесь обычных распределений Эрланга с целью его использования в генераторе GAMMA. Заметим, что числовые характеристики распределений (1) и (3), кроме коэффициента вариации, также отличаются.

Настоящая статья посвящена моделированию СМО HE2/M/1 с гиперэрланговским (HE2) и экспоненциальным (M) входными распределениями в среде GPSS WORLD. В открытом доступе авторам не удалось обнаружить каких-либо результатов для такой СМО.

Постановка задачи

В статье ставится задача построения имитационной модели для СМО HE2/M/1 и подтверждения адекватности построенной математической модели путем численного моделирования в пакете Mathcad. При построении удачной модели для указанной системы построение имитационных моделей систем, включающих распределение HE2 в любой позиции по шкале Кендалла, не будет вызывать затруднения.

Решение задачи

Для построения имитационной модели необходимо задавать значения моментных характеристик распределений HE2 и M, и придется определить неизвестные параметры этих распределений. Моментные характеристики определим через преобразование Лапласа функции (3):

^{+ ( 1 -} P )

' 2 2

^^ 2 + S

A Ч ^s ) = P

_V ² 1 + s

Тогда два первых начальных момента будут:

– для интервалов поступлений

2 p ^{2 ( 1 -} p )   _?=6 p 6(l- p)

• ^T 2    .   ⁺     .        , ^l x.2 ⁺ л 2      ^, (V

2 1        2 2               2 1        2 2

– для времени обслуживания

T = 1 / H    T 2 = 21 H 2 .

Из уравнений моментов (4) найдем неизвестные параметры распределения (3) 21, 22, p. Для этого к (4) добавим выражение для квадрата коэффициента вариации c2 =

Т 2 - ( т₂ )² ( т )²

как связующее условие между (4). Исходя из вида первого уравнения (4) положим

• ² 1 = ⁴ P / ^Т 2 ,    ² 2 = ^{4 ( 1 -} P^ ^Т 2        ⁽⁶⁾

и потребуем выполнения условия (5) [5; 6]. Подставив выражения (6) с учетом (4) в (5), получим уравнение четвертой степени относительно неизвестного параметра p: p(1 - p)[8(1 + c2)p2 -- 8(1 + c2)p + 3] = 0. Отбросив тривиальные решения p = 0 и p = 1, получим квадратное уравнение 8(1 + c\)p2 - 8(1 + c2)p + 3 = 0, решив которое выберем для однозначности больший корень для параметра p:

= 1 + 2(1 + c 2 ) - 3 ^p 2 ^ 8(1 + c 2 )

Отсюда следует, что коэффициент вариации c ₂ >  1 / V2. Подставив (7) в (6), определяем все три неизвестных параметра распределения (3) [5; 6].

Для построения и отладки имитационной модели для системы HE2/M/1 возьмем коэффициент загрузки р = тц / т2 = 0,9, коэффициент вариации интервалов поступлений c2 = 2 и единичное время обслуживания тц = 1. Тогда исходные данные для имитационной модели p = £ + 2(1 + c2) 3 = о, 918, 1 - p = о, 082, 2 N 8(1 + c 2)

2 1 = 3,305, 2 2 = 0,295.

Отсюда средние значения для первой и второй фаз гиперэрланговского распределения 2 / 2 1 = = 0,605, 2 / 2 2 = 6,78 единиц времени.

Приемы аппроксимации законов распределений более подробно описаны в [10–14].

Первый этап построения имитационной модели

На первый взгляд, при построении имитационной модели можно было бы обойтись логическим оператором TEST для перенаправления транзактов в модели с вероятностью p на первую фазу гиперэрланговского закона, а с вероятностью 1 – p – на вторую фазу, как это показано в тексте имитационной модели. Здесь отмечается полная аналогия с аналитической моделью (3) гиперэрланговского закона распределения, т. к. в аналитической модели предполагается мгновенная передача заявок с заданной вероятностью p на первую фазу, а с вероятностью 1 – p – на вторую фазу [7–9; 12].

Анализ результатов прогона модели (рисунок 1) показывает, что в этом случае на первую фазу направляется примерно 82 тыс. транзактов, а на вторую фазу 918 тыс. тразактов, что полностью соответствует заданным вероятностям 0,082 и 0,918. Коэффициент загрузки равен 0,9 и среднее время обслуживания – единица, т. е. исходные

10 ERL1 FVARIABLE (GAMMA(1,0,0.605,2))

20 ERL2 FVARIABLE (GAMMA(1,0,6.78,2))

30 TEST L (RN1),082,MET_1

40 GENERATE V$ERL2

50 TRANSFER ,MET_2

60 MET_1 GENERATE V$ERL1

70 MET_2 QUEUE QCHAN

80 SEIZE CHAN

90 DEPART QCHAN

100 ADVANCE (Exponential (1,0,1.0))

110 RELEASE CHAN

120 TERMINATE 1

130 START 1000000

; Переменная для первой фазы гиперэрланга ; Переменная для второй фазы гиперэрланга ; Если значение случайной величины меньше p

; то генерировать первую фазу и встать в

; очередь к устройству «CHAN», если нет, то

; переход по метке 1 для генерирования

; второй фазы

; Встать в очередь к устройству «CHAN»

; Занять устройство «CHAN»

; Покинуть очередь к устройству «CHAN»

; Задержать транзакт на единичное время

; Освободить устройство «CHAN»

; Удалять по одному транзакту

; Прогон 1 млн транзактов

GPSS World Simulation Report - Untitled Model 1.2.1 Sunday, November 27, 2 022 11:0 0:01

	START TIME 0.000' NAME CHAN ERL1 ERL2 MET_1 MET_2 QCHAN	END TIME 1111087.428	BLOCKS FACILITIES STORAGES
			10          1             0
			VALUE
			10003.000
			10000.000
			10001.000
			4.000
			5.000
			10002.000
LABEL MET_1 MET_2 FACILITY	LOC  BLOCK TYPE 1    TEST 2    GENERATE 3    TRANSFER 4    GENERATE 5    QUEUE 6    SEIZE 7    DEPART 8    ADVANCE 9    RELEASE 10'    TERMINATE ' ENTRIES UTIL	ENTRY COUNT CURRENT COUNT RETRY 0               0               0 81886         0           0 81886         0           0 918139         0           0 1000025       24           0 IC'C'C'C'C'l              1                  0 1000000         0           0 1000000         0           0 1000000         0           0 1000000         0           0 . AVE. TIME AVAIL. OWNER PEND INTER RETRY DELAY
CHAN	IC'C'C'C'C'l 0.90'1	1.001	1     1000001 0     0      0      24
QUEUE	MAX CONT. ENTRY ENTRY(0}		AVE.CONT. AVE.TIME   AVE.(-0) RETRY
QCHAN	58   25 | 1000025 128109		5.898     6.553     7.515     0

Рисунок 1. Результаты прогона имитационной модели

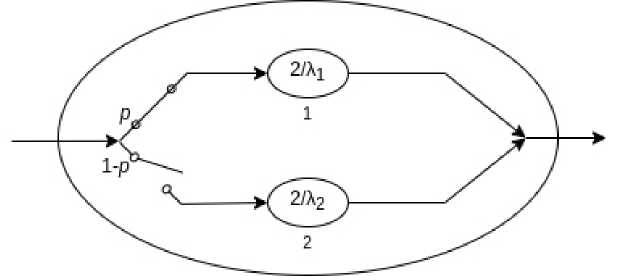
Рисунок 2. Формирование двухфазного гиперэрланговского распределения

данные и результаты моделирования совпадают. Коэффициент загрузки ρ в аналитике так же, как и в имитационном моделировании, определяется отношением средних интервалов р = Т_ц / Т_х . Результат по среднему времени ожидания в очереди 6,553 не соответствует аналитической модели [5; 6], которая дает 22,59 единиц времени.

Второй этап построения имитационной модели

Выше мы убедились, что копирование аналитики в имитационном моделировании не дает нужного эффекта. Дискретно-событийное моделирование работает по своим установленным алгоритмам. Внимательно смотрим на двухфазное формирование гиперэрланговского распределения для имитационного моделирования (рисунок 2).

На рисунке 2 показано, что с вероятностью p сформированный транзакт отправляется на пер-

10 P_1 EQU 0.082

20 P_2 EQU (1-P_1)

30 T_1 EQU 3.39

40 T_2 EQU 0.302

50 GENERATE ,,,1

60 Switch TRANSFER P_1,Met_2,Met_1

70 Met_1 TRANSFER ,Kl_1

80 Met_2 TRANSFER ,Kl_2

90 Kl_1 LOGIC S Kluch1

100 ADVANCE (T_1#3.1)

110 LOGIC R Kluch1

120 TRANSFER ,Switch

130 Kl_2 LOGIC S Kluch2

140 ADVANCE (T_2#3.1)

150 LOGIC R Kluch2

160 TRANSFER ,Switch

170 GENERATE (GAMMA(11,0,T_1,2))

180 GATE LS Kluch1,Met_10

190 TRANSFER ,Met_20

200 GENERATE (GAMMA(21,0,T_2,2))

210 GATE LS Kluch2,Met_10

вую фазу гиперэрланговского закона со средним интервалом 2/λ₁, а с вероятностью 1 – p – на вторую фазу со средним интервалом 2/λ₂. В схему включены логические переключатели – объекты, которые могут находиться только в двух состояниях: включен, выключен. Эти два состояния управляются с помощью логического оператора LOGIC X A. Здесь A – имя логического ключа, X – логический оператор, задающий тип операции: S – включить, R – выключить.

В схеме попеременно в зависимости от значения вероятности p должны будут работать два переключателя, которые в тексте программы обозначены Kluch1 и Kluch2. Введение в схему логических переключателей еще не решает проблему создания имитационной модели, т. к. в соответствующие фазы нужно впустить сгенерированный прежде транзакт при включенном переключателе.

; Значение вероятности р1 1-й эрланговской

; фазы гиперэрланговского распределения

; Значение вероятности р2 2-й эрланговской

; фазы; гиперэрланговского распределения

; Значение среднего интервала 1-й

; эрланговской фазы

; Значение среднего интервала 2-й

; эрланговской фазы

; Генерация одного транзакта управления

; ключами выбора эрланговской фазы

; Включение 1-го ключа с вероятностью р1,

; а 2-го – с вероятностью р2

; Отправить транзакт на 1-й ключ «Kl_1»

; Отправить транзакт на 2-й ключ «Kl_2»

; Включить ключ 1-й эрланговской фазы

; Время работы ключа

; Выключить ключ 1-й эрланговской фазы

; Отправить транзакт на выбор рабочего ключа

; «Switch»

; Включить ключ 2-й эрланговской фазы

; Время работы ключа

; Выключить ключ 2-й эрланговской фазы

; Отправить транзакт на выбор рабочего ключа

; «Switch»

; Генерация 1-й эрланговской фазы

; Определения состояния 1-го ключа (если

; «включен»–переход к следующей строке

; программы, если «выключен» – переход на

; Met10)

; Переход по метке

; Генерация 2-й эрланговской фазы

; Определение состояния 2-го ключа

; аналогично 1-му

220 Met_20 QUEUE QCHAN

230 SEIZE CHAN

240 DEPART QCHAN

250 ADVANCE (Exponential(31,0,1.0))

260 RELEASE CHAN

270 TERMINATE 1

280 Met_10 TERMINATE

290 START 1000000

; Встать в очередь к устройству «CHAN»

; Занять устройство «CHAN»

; Освободить одно место в очереди

; Задержать на обслуживании на единичное

; время

; Освободить устройство «CHAN»

; Удалять по одному транзакту

; Удалить транзакты из модели

• ; Прогон 1 млн. транзактов

GPSS World Simulation Report - Untitled Model 1.3.1

	Wednesday,	November 24, 2 022	11:22:02
	START TIME	END TIME BLOCKS	FACILITIES STORAGES
	0.000'	1114430.513 24	1              0
	NAME		VALUE
	CHAN		1C0C6. COO'
	KLUCH1		10'007.000
	KLUCH2		10004.000'
	KL_1		5. COO'
	KL_2		9.000'
	MET_1		3. COO'
	MET_10		24 . COO'
	MET_2		4 . COO'
	MET_2C		18 . COO'
	P_1		0.082
	P_2		0.918
	QCHAN		1000'5. COO'
	SWITCH		2 . COO'
	T_1		3.390
	T 2		0.302
LABEL LOC	BLOCK TYPE	ENTRY COUNT CURRENT COUNT RETRY
1	GENERATE	1	O'                   O'
SWITCH 2	TRANSFER	645960'	O'                0
MET_1    3	TRANSFER	53243	O'                0
MET_2    4	TRANSFER	592717	O'                   O'
KL_1     5	LOGIC	53243	O'                0
6	ADVANCE	53243	1                O'
7	LOGIC	53242	0'                   0'
8	TRANSFER	53242	O'                0
KL_2     9	LOGIC	592717	O'                   O'
10	ADVANCE	592717	O'                0
11	LOGIC	592717	O'                   O'
12	TRANSFER	592717	O'                   O'
13	GENERATE	163979	O'                0
14	GATE	163979	O'                   O'
15	TRANSFER	82361	O'                   O'
16	GENERATE	1844133	O'                0
17	GATE	1844133	O'                   O'
MET_20 18	QUEUE	1000002	1          0
19	SEIZE	1000001	1                O'
20'	DEPART	1000000	O'                   O'
21	ADVANCE	100000 O'	O'                0
22	RELEASE	1000000	O'                   O'
23	TERMINATE	100000 O'	O'                   O'
MET 10 24	TERMINATE	1008110'	O'                0

FACILITY ENTRIES UTIL. AVE. TIME AVAIL. OWNER PEND INTER RETRY DELAY

CHAN 1000001 0.898   1.000     1    2008099  0    0 O' 1

OCHAN        175   2 1000002 52010   20.300     22.623    23.864   0

Это достигается следующим логическим оператором GATE (впустить). Его формат: GATE X A,[B], где A – имя проверяемого объекта; B – номер блока, к которому переходит транзакт, если положение объекта не отвечает условию проверки; X – логический оператор с множеством значений, проверяющий условие, которое должно быть выполнено для объекта в текущий момент для успешного завершения проверки. В нашем случае объектом A является переключатель Kluch1 или Kluch2, а положение объекта LS – логический ключ включен.

В имитационной модели с применением логических ключей необходимо указать еще продолжительность их работы, в тексте программы – это время для первого ключа равно T_1#3.1, а для второго – T_2#3.1. Здесь T_1 и T_2 – средние интервалы для фаз, # операция арифметического умножения. Константа 3.1 должна подбираться экспериментально так, чтобы показатели работы СМО не отклонялись от реальных значений. В этом состоит недостаток имитационной модели с использованием составных распределений и логических переключателей.

Из результатов имитации на рисунке 3 следует, что коэффициент загрузки равен 0,9 и среднее время обслуживания – единица, т. е. исходные данные для примера и результаты моделирования совпадают. Среднее время ожидания заявок в очереди в 22,623 единицы времени практически совпадает с результатом численного моделирования 22, 59. Средняя длина очереди в модели 20,30 также практически совпадает с результатом численного моделирования 20,33.

Заключение

В работе представлены разработанные алгоритм и имитационная модель для имитации функционирования СМО HE2/M/1 с гиперэрлан-говским входным распределением второго порядка. В ходе разработки имитационной модели был использован сложный механизм логических переключателей фаз закона распределения, что позволило построить адекватную имитационную модель продвижения транзактов внутри модели. Полученные результаты публикуются впервые.