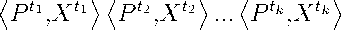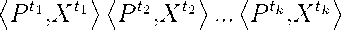Проблема интегрируемости и обобщённый непараметрическиймето Д анализа потребительского спроса

Индексы потребительских цен и спроса являются обобщёнными характеристиками, позволяющими судить о тенденциях эволюции экономики. Исходной информацией для их построения является торговая статистика, представляющая собой набор цен и объёмов потребления в различные периоды времени.

Опишем традиционный подход к построению индексов, который опирается на оценку стоимости потребительской корзины. Рассмотрим группу, состоящую из m видов товаров. Обозначим через X вектор потребления этих товаров, а через p — вектор цен на них. Стоимость корзины товаров X , продаваемых по ценам p , равна скалярному произведению LpX) . Примем период t в качестве базового, а период τ —в качестве текущего. В указанных обозначениях индексом цен Ласпейреса называется отношение (p ^T ,X t ^ / Lp,X t ) , в котором в качестве потребительской корзины выбирается набор товаров, купленных потребителями в базовый период. Статистические службы обычно вычисляют этот индекс потребительских цен.

Отметим, что выбор потребительской корзины не является обоснованным. Если в качестве корзины выбрать набор товаров потребляемых в текущий период, то получим величину (pT,Xт) / (pt,Xт), на- зываемую индексом цен Пааше. Вычисления показывают, что, как правило, значение индекса Пааше не превосходит значения индекса Ласпейреса. Систематическое различие между этими двумя индексами называется эффектом Гершенкрона. Эффект Гершенкрона отражает замещение относительно подорожавших товаров подешевевшими товарами. В работе А.А. Ко-нюса [1] был предложен подход к определению индексов потребительских цен, учитывающий изменение спроса (потребительской корзины) при изменении цен и основанный на паретовской теории потребительского спроса. В основе паретовской теории лежит гипотеза о возможности описания потребительского поведения моделью рационального репрезентативного потребителя, выбирающего наилучший потребительский набор, доступный в силу бюджетных ограничений.

• II.    Постановка задачи о рациональности поведения потребителей

Будем описывать поведение потребителей с помощью обратных функций спроса P ( X ) = ( P 1 ( X ) , ..., P m ( X )), выражающих зависимость между объёмами потребления товаров X = ( X 1 , ..., X m ) и ценами на них. Будем предполагать, что функции P ( X ) непрерывны на R m .

Определение 1. Будем говорить, что обратные функции спроса P ( X ) рационализируемы в классе функций полезности Ф , если существует такая функция F ( X ) е Ф , что

X е Argmax{F(Y) |(P(X) ,Y) <

< (P ( X ) ,X),Y е R m }.

Будем при этом говорить, что функция полезности F ( X ) рационализирует обратные функции спроса P ( X ) .

Функции полезности должны удовлетворять априорным условиям, то есть принадлежать классу Ф д вогнутых, положительно-однородных первой степени, непрерывных на множестве R m функций, положительных на множестве int R m .

Предложение 1. Если функция F ( X ) е Ф д рационализирует обратные функции спроса P ( X ) , то

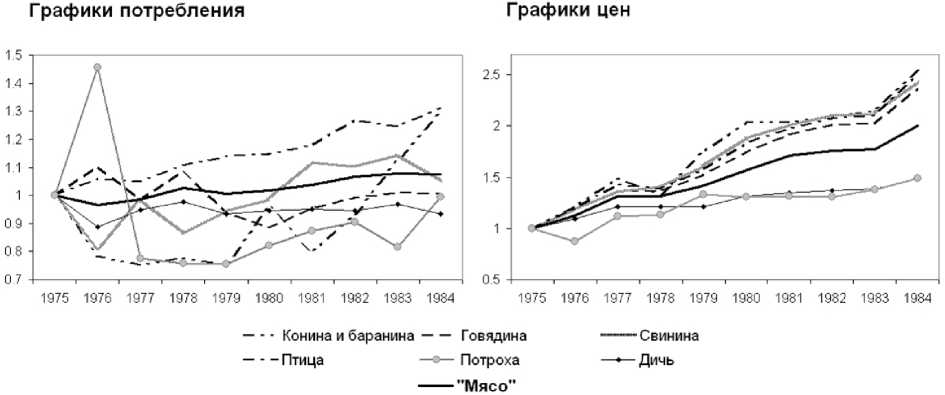
X е Argmax

- QPX)(P(X > Y>Y е R m}, где функция Q (p) является преобразованием Янга функции F (X), то есть где dF (X) супердифференциал вогнутой функции F (X) в точке X е int Rm. В случае, когда F (X) является дифференцируемой функцией, соотношение (3) принимает вид основной формулы теории экономических индексов

1^m

dF(X) = Q (P( X)) ^ Pj(X) dXj,  <4> согласно которой, чтобы посчитать изменение индекса спроса Конюса (функции полезности) F (X), надо посчитать отношение стоимости изменений в объёмах покупаемых товаров dX = (dXi, ..., dXm) в текущих ценах P (X) к текущему значению индекса цен Q (P (X)), который связан с индексом спроса F (X) преобразованием Янга (1). Таким образом, проблема построения индексов Конюса спроса F (X) и цен Q (p) сводится к проблеме существования и поиска интегрирующего множителя Q(P(X)) для дифференциальной формы обратных функций спроса

ш = jr Pj (X) dXj. j=i

В литературе по теории экономических индексов (см., например, [2], с. 143) большой популярностью пользуются индексы Диви-

Q (Р) = inf { Ш

F⁽X)

X > 0,F(X) > с! .

зиа, согласно которым отношение индекса спроса F (X (t)) в текущий период времени t к индексу спроса F (X (т)) в базовый период времени τ определяется по форму-

Доказательство предложения 1 получается применением теоремы Куна–Таккера к задаче вогнутого программирования

max{F (Y) |(P (X) ,Y} <

< (P(X),X),Y е Rm},       (2)

в которой множитель Лагранжа к ограничению (P(X) ,Y) ^ (P(X) ,X) равняется

Q ( p (X)).

Необходимое и достаточное условие максимума для задачи (2) в дифференциальной форме для X е int Rm имеет вид

QMXj)P е dF (X>,    <3> ле

F (X (t)) =

F (X (т))

_    (f Е m=i p. (X (в)) ха ,,

p U Е ’=1 p. (X (в)) X. (в)de

τ

Отметим, что если существует интегрирующий множитель для дифференциальной формы обратных функций спроса ω ,то есть справедлива формула (4), то индекс Конюса совпадает с индексом Дивизиа.

• III.    Свойства преобразования Янга

Известно (см. [3], с. 230–233), что преобразование переводит функции из класса

Фо в функции из класса Фо и что для любой функции F (X) E Фо и связанной с ней формулой (1) функции Q (p) справедливо соотношение

Поскольку ^P,X^ = F (X} = 1 = Q PУ неравенство (8) эквивалентно

F (X) = inf /QX | Q (p) > 0 ,p E Rm-j , P                      (5)

то есть преобразование Янга инволютивно на классе Фо .

Любая положительно однородная функция однозначно определяется сво-

Q (P) ^ (P,X^ .

Но неравенство (9) справедливо для любых P E Rm, так как из (5) следует, что

P P,X QQ Q (P) F^X) = Q (P).

ей поверхностью

уровня. Поэтому функ-

ции F (X) E Фо и Q (p) E Фо однознач-

Предложение 2 доказано.

Вторые квадратичные формы поверх-

но определяются ностями Q F =

соответственно поверх-

{X E Rm IF (X) = 1 } и

ностей QF

{X E Rm IF (X) = 1} и

Qq = {P E Rm |Q (P) = 1 }. Геометрический смысл преобразования Янга сформулирован в следующем предложении.

Предложение 2. F (X) E Фо, X E Qf и P E QQ X e dQ^P).

Если функция

P E dF (X}, то

Доказательство. По определению супердифференциала из P E dF (X) имеем, что для любого X E Rm справедливо неравенство

F (X) — F (X) < ^P,X — X^ .  (6)

Если выбрать в (6) X = XX, где X > 0, то с учётом положительной однородности получаем, что при X > 0 справедливо неравенство (X — 1) F (X) ^ (X — 1) ^ P,X ^. Откуда следует обобщённое тождество Эйлера для вогнутых положительно однородных функций

Qq = {P E Rm |Q (P) = 1} могут быть заданы с помощью матриц эластичностей замещения, которые в соответствующих точках X E Qf и P E Qq,P E dF (x) оказываются взаимно обратными (подробнее, см. [4], с. 115)

Поскольку переход от соотношения (3) к основной формуле теории экономических индексов (4) предполагает дифференцируемость функции полезности F (X ), представляет интерес выделение класса дифференцируемых функций полезности, на котором преобразование Янга инволю-тивно.

Определение 2. Будем говорить, что функция F (X) принадлежит классу Ф1, если выполнены следующие условия:

1) F (X) E C^{1 (}Rm⁾; 2) F (X) > 0 при X E int Rm; 3) F(XX) = XF(X) при X> 0, X Q 0; 4) grad F (X) > 0 при X E int Rm; 5) F(X) — строго квазивогнута на Rm; 6) для любого P E int Rm существует хотя бы одно решение задачи

^F X) = ^,Х) .

inf {jP|^ IX E int Rmd .

F (X)

В силу этого тождества неравенство (6) означает, что для любых X E Rm справедливо F (X) ^ PF*^У то есть с учётом (7) имеем Q PP) = 1 и, значит, P E Qq . Соотношение X E dQ PP^ эквивалентно выполнению для любых P E Rm неравенства

Из результатов, полученных в [5], следует, что преобразование переводит функции из класса Ф1 в функции из класса Ф1 и что преобразование Янга инволютивно на классе Ф1.

IV. Критерий существования функции полезности (гладкий случай)

Q (P) — Q^P) < PP — P,Xy   (8)

Обозначим M = {1, ..., m}.

Теорема 1 (см. [6–8]). Пусть обратные функции спроса P (X) Е C¹R+ m). Для того чтобы функции P (X) были рационализируемы в классе функций полезности Ф1, необходимо и достаточно, чтобы они удовлетворяли следующим условиям:

• 1.    P (X) > 0 при X Е int Rm;

• 2.    для любых i Е M, j Е M, X > 0, X Е int Rm справедливо соотношение

• 3.    для любых X Е int Rm, Y Е int Rm, таких, что ни при каком X > 0 Y = XX, выполнено неравенство:

• 4.    для любых i Е M, j Е M, k Е M, X Е int Rm справедливо равенство:

• 5.    для любого X = (X 1 ,..,Xm) Е Rmm справедливо соотношение:

Pi (XX) = Pi (X) Pj (XX)   Pj (X) ’

(P (X) ,Y) (P (Y) ,X) >

(P (X) ,X) (P (Y) ,Y) ’

Pi(X) (H(X) - H(X 0+

+Pj(X) (H(X> - IX < X))+ +P(X) (Hj < X)- ж, < X >)=0’

(M\ {i Е M \Xi = 0 }) П n{j Е M\Pj (X) = 0} = 0.

Условия 1 и 5 теоремы носят технический характер и связаны с выбором класса функций полезности Ф1. Условие 2 называется условием отделимости и выражает полноту номенклатуры рассматриваемой группы товаров, для которой существует соответствие между пропорциями цен и пропорциями спроса на товары. Условие 3 обеспечивает строгую вогнутость поверхностей уровня QF = {X Е Rm \F (X) = 1}, Qq = {P Е Rm \Q (P) = 1} и выражает эффект Гершенкрона: индекс цен Ласпей-реса больше индекса цен Пааше. Условие 3 является следствием закона Хикса (см. [7]), который выражает в терминах обратных функций спроса «Закон убывания предельной производительности» и согласно которому для любого вектора v = (v 1, .... vm), такого, что (P (X) ,v) = 0, справедливо неравенство mm

I? a

зр_г (X)

∂Xj

vivj

< 0.

Можно показать, что условие 3 является условием типа неравенства, то есть сохраняется при малых возмущениях функций P (X) в норме пространства C¹ (Rm). Напротив, условие 4, известное как условие интегрируемости Фробениуса, выражает критерий существования интегрирующего множителя для дифференциальной формы обратных функций спроса ω ияв-ляется условием типа равенства. Оно нарушается при малых возмущениях функций P (X) в норме пространства C¹ (Rm). Существование экономических индексов является одним из постулатов современной экономической теории, объясняющим возможность регулировать потоки разнообразных товаров, номенклатура которых составляет порядка 10⁹наименований, с помощью «скалярной» обратной связи — финансовых потоков. Поэтому нарушение условий Фробениуса при малых возмущениях воспринималось экономистами как проблема интегрируемости (см. [6,9]).

Появление в экономической литературе условий интегрируемости восходит к работе Дж. Антонелли [6], впервые опубликованной в 1886 году. Однако внимание экономистов к проблеме интегрируемости было привлечено работой В. Вольтерра, впервые опубликованной в 1906 г. В виде условий четыре условия интегрируемости были получены Е.Е. Слуцким в работе [10], впервые опубликованной в 1915 г. В тот же период К. Каратеодори сформулировал второе начало термодинамики в форме существования интегрирующего множителя для дифференциальной формы тепла. Из этой формулировки следовало, что уравнения состояния, химические потенциалы, внутренняя энергия задаются функциями, которые удовлетворяют условиям интегрируемости Фробениуса и, значит, не являются функциями общего положения. Поэтому возник вопрос: являются ли условия интегрируемости дифференциальной формы обратных функций спроса ω фундаментальным законом, подобным второму началу термодинамики?

Анализу выполнимости и интерпретации условий интегрируемости для дифференциальной формы обратных функций спроса ω посвящены работы многих известных экономистов XX века, таких, как В. Парето, П. Самуэльсон, Дж. Хикс, Х. Хотел-лин, Х. Хаутеккер, К. Эрроу, Л. Гурвиц, Х. Удзава, Д. Гейл, М. Рихтер и др. Их усилия привели к созданию теории выявленного предпочтения, в терминах которой удалось переформулировать условия рациональности поведения в форме удобной для эмпирической проверки.

• V. Выявленные предпочтения и критерий существования функции полезности (негладкий случай)

Понятие выявленного предпочтения было введено П. Самуэльсоном в [11] следующим образом.

Определение 3. Считается, что X E Rm выявлено предпочтительнее Y E Rm (X >- Y), если выполняется неравенство (P (X) .X) > (P (X) .Y).

П. Самуэльсон, развивая концепцию рационального репрезентативного потребителя, вкладывал следующий содержательный смыл в определение. При ценах P (X) набор товаров Y стоил (P (X) .Y) и был доступен потребителю, располагающему бюджетом в (P (X) .X). Поскольку ценам P (X) соответствует приобретение набора товаров X, набор товаров X выявлено предпочтительнее доступного в силу бюджетных ограничений набора товаров Y .

П. Самуэльсон сформулировал следующее свойство, которое при размерности номенклатуры m = 2 является необходимым и достаточным условием рационализируе-мости обратных функций спроса в классе функций полезности Фо, и высказал гипотезу о том, что результат можно обобщить на произвольные m ^ 2.

Слабая аксиома теории выявленного предпочтения. Если X E Rm и Y E RmX У Y и Y У X, то (P (X) .X) = (P (X) .Y) и (P (Y) ,Y) = (P (Y) X).

Предложение 3. Пусть (P(X) ,X) > 0 при любых X E Rm\ {0} и выполнено условие отделимости (условие 2 теоремы 1).

Для того, чтобы для любой пары точек из множества {AX |A > 0} U {цY \ц > 0} выполнялась слабая аксиома теории выявленного предпочтения, необходимо и достаточно, чтобы было справедливо неравенство

(P (X) Y) (P (Y) X) >

• >(P (X) X)(P (Y) Y).     (10)

Доказательство.

Необходимость. Выберем ц 1 > 0 таким, что

• (P (X) .X) = (P (X) ц 1Y).      (11)

Тогда в силу слабой аксиомы теории выявленного предпочтения имеем, что (P (цi Y) цi Y)< (P (цiY) ,X). Откуда в силу условия отделимости получаем, что

• (P (Y) цi Y)< (P (Y) .X).    (12)

Перемножая соотношения (11) и (12) и сокращая на ц 1 > 0, получаем (10). Необходимость доказана.

Достаточность. Пусть A 1 X >- ц 1 Y и ц 1 Y У A 1 X, где A 1 > 0, ц 1 > 0. С учётом условия отделимости имеем, что (P (X) .A1X) > (P (X) .ц 1Y) и (P (Y) .цiY) > (P (Y) .AiX). Перемножая эти неравенства и сокращая на положительный множитель λ1μ1, получаем (P(X).Y)(P(Y).X)< (P(X).X)(P(Y).Y). Откуда в силу (10) имеем

(P (X) .Y )(P (Y) .X) = (P (X) .X )(P (Y) .Y).

Следовательно, (P(X).A_iX) = (P(X).ц_iY) и (P (Y) .цiY) = (P (Y) .AiX). Достаточность доказана.

Однородная слабая аксиома теории выявленного предпочтения. Для любых X E Rm и Y E Rm справедливо неравенство

(P (X) Y) (P (Y) .X) >

• >(P (X) .X) (P (Y) Y).

Отметим, что однородная слабая аксиома теории выявленного предпочтения эквивалентна эффекту Гершенкрона.

В работе [12] Х. Хаутеккер предложил более сильное требование необходимое и достаточное для рационализируемости обратных функций спроса в классе функций полезности Ф_о.

Сильная аксиома теории выявленного предпочтения. Если к * 2, 1       m2       m        k       m

.^X Е Vl + , .^X     Е Vl + , ..., ■^X     Е + и X1 ^ X2, ..., Xk-1 ^ Xk, Xk ^ X1, то (P (X 1) ,Х1)   =   (P (X 1) ,X 2 Y

..., (p(xk- 1),xk-¹} =   (p(xk- 1),xky

(P (X k) ,X k^ = (p (X k) ,X¹).

Слабая аксиома теории выявленного предпочтения следует из сильной аксиомы теории выявленного предпочтения при к = 2. Вплоть до работы [13] предпринимались попытки установить эквивалентность слабой и сильной аксиомы. Д. Гейл [13] построил пример обратных функций спроса, удовлетворяющих слабой аксиоме теории выявленного предпочтения, но не рационализируемых.

Необходимость выполнения сильной аксиомы для рационализируемости обратных функций спроса P (X) с помощью функции полезности F (X) Е Фо следует из соотношений (3) и определения супердифференциала. Действительно, если X¹Е Rm, X²Е Rm, ..., Xk Е Rm и X¹^ X², ..., Xk-¹^ Xk, Xk ^ X 1, то

• -    - ( «^ X - - Е *

* F (X2) - F (X 1) , ...,

• 0    * (k- х k- 1) *

• -    F (Xk) - F (Xk-1) ,

• ⁰    * ( «Ж ^{x 1 - X}k) *

* F (X1) - F (X k) .

Складывая последние неравенства, получаем, что

• -    * i^ (^-v x>

• -    («ЕЕ,^{X- X}k) *¹

Откуда следует, что

• < P (X¹) ,X 1) = (P (X 1) ,X2} ,...,

(P Xkk- 1) ,Xk^- 1} = (P (Xk^- 1) ,Xk) ,

(P⁽Xk⁾,Xk^}= ( P⁽Xk⁾,X^1}, то есть справедливость сильной аксиомы.

Предложенное в [12] доказательство достаточности содержало пробелы, которые впоследствии заполнялись в серии статей. По-видимому, впервые полное доказательство было получено в [14]. Доказательство достаточности может быть основано на использовании теоремы Каратео-дори–Рашевского–Чжоу20 о том, что если в некоторой точке нарушены условия интегрируемости Фробениуса, то в любой сколь угодно малой окрестности этой точки существует гладкая замкнутая кривая X (t), t Е [0,1], X (0) = X (1), во всех точках которой, кроме быть может двух справедливо неравенство jm P, (X(t)) d-XX > -. j=1

Проводя дискретизацию, заменяя производную разностными отношениями, можно установить нарушение сильной аксиомы. Трудности возникают при прохождении двух исключенных точек, они преодолеваются с помощью результатов Х. Уза-вы ( [6], с. 7–28). Подробное доказательство, основанное на этом подходе, содержится в [7].

Предложение 3’. Пусть (P(X) ,X) > 0 при любых X Е Rm\ {0} и выполнено условие отделимости (условие 2 теоремы 1). Для того чтобы для любого набора точек из множества {AX¹|A > 0}U{AX²|A > 0}U...U{AXk |A > 0 } выполнялась сильная аксиома теории выявленного предпочтения, необходимо и достаточно, чтобы для любого упорядоченного набора {t 1, ..., tk} C {0,T^ было справедливо неравенство

/Pt¹,Xt²\ /Pt²,Xt³) ... /Ptk,Xt¹) *

*

Доказательство предложения 3’ аналогично доказательству предложения 3.

Определение 4. Будем говорить, что обратные функции спроса P(X) удовлетворяют однородной сильной аксиоме (ОСА), если для любого набора векторов

• {X¹, ...XT} из Rm справедливо неравенство

(P(X 1),X²\ (P(X2),X³\ ... (P(XT),X^1]>

• >/P(X 1),X 1} /P(X²),X²]... /P(XT),XT}.

Теорема 2 ( [16, 17]). Пусть P(X) — неотрицательная, непрерывная на Rm вектор-функция, такая, что (P(X) ,X] > 0 при любых X Е Rm\ {0}. Тогда следующие утверждения эквивалентны.

• 1.    Обратные функции спроса P (X) рационализируемы в классе функций полезности Ф_о.

• 2.    Система линейных неравенств

• 3.    Обратные функции спроса P (X) удовлетворяют ОСА.

• 4.    Существуют такие индексы цены Q(P) и спроса F(X) из класса Ф₀, что для любых P и X из Rm выполняется неравенство Q(P)F(X) ^ (P,XY В случае, когда P = P(X), будет достигаться равенство Q (P (X)) F (X) = (P (X] ,Х].

А(Y) (P(Y) ,Х] > А (X) (P(X) ,Х], (13)

где X Е Rm, Y Е Rm, имеет решение А(X), положительное и непрерывное на int Rm.

Следствие. Индексы спроса F(X) и цены Q(P) можно выразить следующим образом через решение А(X) системы (13):

F (X) = А (X) (P (X) ,X),

, , _         1

Q^(P(X)) = _Ж).

• VI. Непараметрический метод построения экономических индексов

Исходной информацией для вычисления индексов цен и спроса служит торговая статистика {Pt,Xt}To данной группы товаров, которая определяет значения обратных функций спроса в конечном числе точек {Xt}T0. В работах [18]-[21] раци-онализируемость торговой статистики понимается как возможность продолжить её до обратных функций спроса, рационализируемых в классе Фо. Теория выявленного предпочтения позволяет конструктивно проверять по торговой статистике, удовлетворяет ли она гипотезе о рациональности поведения и вычислять индексы Коню-са. В основе алгоритмов проверки лежит следующая теорема, являющаяся дискретным аналогом теоремы 2.

Теорема 3 (Африата–Вериа-на) [17, 19]. Следующие свойства торговой статистики эквивалентны:

• 1)    существует функция полезности F (X) Е Ф₀, рационализирующая торговую статистику, то есть

Xt Е Argmax{F(X)\(PtX)<

< (PtXt^X > 0},t = 0, ..., T;

• 2)    торговая статистика {Pt,Xt}T₀ удовлетворяет ОСА, то есть для любого упорядоченного набора моментов времени {t 1, ..., tk} C {0, ..., T} выполняются неравенства

  >

  
  

  /pt 1 ,xt2\ /pt2,xt³} ... /Ptk,Xt¹} >

  3) существует решение (А₀, ..., А_Т) > 0 системы линейных неравенств:

  
  

Ат (P^т,X^t) ^ Аt (P^t,X^t), T,t = 0, ..., T;

• 4)    существует функция полезности, рационализирующая торговую статистику, вида

F (^X )= ^m ‘Я ^А‘<^Pt,X).

Отметим, что аналог теоремы Афри-ата–Вериана о рационализации обратных функций спроса в классе гладких функций полезности получен в [22].

Решение системы (14) можно найти с помощью вычислительного алгоритма Варшалла–Флойда. Обозначим коэффициенты матрицы индексов цен Пааше через

_ (Ptxt] ^Tt    (Pт Xt] .

В новых переменных система (14) имеет вид

АtCтt< Ат.              (15)

Определим C_τ^∗_t как максимум по всем возможным упорядоченным подмножествам {t 1 ,t₂, ..., tk} множества T = {0,1, ..., T}

{t 1 ,t2, ..., tk} C T,k > 0}.

Из теоремы Африата–Вериана следует, что система (15) разрешима тогда и только тогда, когда C_t*_t ^ 1, t E T. Можно заметить, что если система (15) имеет решение, то она эквивалентна системе

XtCTt < Хт.              (16)

Алгоритм Варшалла–Флойда. Рассмотрим идемпотентное полукольцо с операциями a ⊕ b = max(a,b) и a ⊗ b = ab. Тогда

C^∗=C⊕C^•2⊕...⊕C^•k⊕...,     (17)

где C•n означает возведение матрицы в степень n в идемпотентном смысле (то есть все операции суммирования заменяются операцией ⊕ взятия максимума). Отметим, что все элементы матрицы C положительны. Если на каком-то шаге n< T вычисления идемпотентных степеней выясняется, что Ct∗t > 1, то все элементы матрицы C∗ равны +∞, и система неразрешима. В противном случае для вычисления ряда (17) достаточно ограничиться первыми T слагаемыми, и, таким образом, алгоритм вычисления C∗ имеет сложность порядка T 3 .

Если система (16) имеет решение, то набор переменных

λt =maxCt∗β,t∈ Tˆ β∈Tˆ является решением системы (15), а значит, и решением (14).

По положительному решению системы (14) можно построить временные ряды индексов потребительских цен Конюса

{1/λt}t^T=0

и индексов спроса Конюса

λt Pt,Xt tT=0, которые учитывают изменения структуры потребления. Такой метод построения экономических индексов называется непараметрическим методом (см. [23, 24]).

Рис. 1

В работах [24–26] проводились эмпирические исследования, которые показали, что условия интегрируемости могут нарушаться в периоды структурных перестроек в экономике. Например, анализ торговой статистики потребления продуктов питания в Швеции за период 1921–1937 годы показал, что для выполнения условий рацонализируемости надо исключить из временного ряда статистику за 1933–1935 годы, в которые происходила смена технологических укладов после Великой экономической депрессии 30-х годов XX века. На рис. 1 изображены исходная торговая статистика Венгрии за 1975–1984 гг. и результаты вычисления индексов Коню- са цен и спроса для группы мясных продуктов. Как видно из рисунка, вычисленные с помощью непараметрического метода индексы Конюса медленнее изменяются со временем, чем исходная торговая статистика. Поэтому прогнозирование следующих по времени значений торговой статистики, как правило, менее точно, чем прогнозирование соответствующих значений индексов цен и спроса.

• VI I. Непараметрический метод анализа сегментации потребительского рынка и прогнозирование спроса

В отличие от методов вычисления индексов Ласпейреса или Паше непараметрический метод построения экономических индексов может использоваться для анализа потребительского спроса.

Определение 5. Группа товаров Y = (Y1, ..., Yn) отделяется от остальной номенклатуры товаров Z = (Zi, ..., Zm-n), если перестановкой компонент вектор товаров X = (X 1, ..., Xm) можно представить в виде (Y,Z) и функция полезности выражается в виде суперпозиции F (X) = Fо (Fi (Y) ,Z).

Нетрудно показать (см. [25]), что если функции F0 (•) и F1 (•) непрерывно дифференцируемы, то обратные функции спроса на товары из группы Y удовлетворяют условию отделимости в следующей форме: для любых А > 0, Y Е int R +, Z Е Rm^-n, W Е Rm^-n

Pi" (AY,Z) Pi" (Y,W) Pj (AY,Z) Pj (YW)'

Здесь P^ (Y,Z) — обратная функция спроса на i-й товар из выделенной группы товаров Y .

Свойства отделимости отражают сегментацию потребительского рынка и являются важной структурной характеристикой потребительского спроса. Обычно вычисление экономических индексов статистическими службами представляет иерархически организованный, многоуровневый процесс.

Предложение 4   [25]. Пусть функция полезности F (X)   Е   Фо и представима как суперпозиция F (X) = Fо (Fi (Y1), ..., Fk (Yk) ,Z), где перестановкой компонент вектор товаров X = (X 1, ..., Xm) можно представить в виде (Y1, ..., YkZ . Здесь Y1 Е Rn, ..., Yk Е Rnk, Z Е R+ , ni + ... + Пк + l = m-. Тогда преобразование Янга Q (P) функции F (X ) представляется как суперпозиция Q (P) = Qо (Qi (PY1), ..., Qk (PYk) ,PZ), где вектор цен P после той же перестановки компонент представляется в виде PPY,1, ..., PY,k,PZ), а функции Qо (•) ,Q 1 (•), ..., Qk (•) являются преобразованиями Янга функций Fо (•) ,Fi (•), ..., Fk (•) соответственно. Здесь PY,1 Е Rn1, ..., PY,k Е Rnk,PZ Е Rl+.

Предположим, что исходная торговая статистика {Pt,Xt}^o удовлетворяет однородной сильной аксиоме. Обозначим через Г(P) множество, состоящее из векторов X Е Rm, для которых торговая статистика {Pt,Xt}t=₀, расширенная на набор (P,X), удовлетворяет однородной сильной аксиоме. Прогноз структуры потребления будем описывать множеством Г(P).

Вычислим коэффициенты

C*. =       max к^1 ,{t 1, ..., tk}с{о, ..., T}

{

(Pt¹,Xt¹) (Pt,Xt}

^TX t 1) (Ptk X t)

k

П i=2

(Pti ,Xti} (Pti-1 ,Xti}

с помощью алгоритма Варшалла–Флойда.

Предложение 5. Пусть торговая статистика {Pt,Xt}T=₀рационализируема. Положим

7 (PA =---1--- min   / (P,X } I

Yt ( '    (PT,XT} 16|о, ...,t}[ CtT Г t = 0, ..., T. Тогда

Г(P) = {X Е RmiYT(P)(P^T,X} > (P,X}, t = 0, ..., T}.

На основе предложения 5 и прогноза суммарных потребительских расходов на продукты из рассматриваемой группы товаров можно предложить следующий подход к прогнозированию спроса. На первом шаге выбирается отделимая группа товаров, содержащая номенклатуру прогнозируемых товаров. Исследуется сегментация рынка выделенных товаров. На втором шаге по торговой статистике {(Pt,Xt) |t = 0, ..., T} строится временной ряд потребительских расходов {Фt = (Рt,Xt) \t = 0, ..., T}. На третьем шаге по временным рядам {Рt,Фt \t = 0,.,.,T} осуществляется прогноз потребительских расходов Ф и вектора цен P . На четвертом шаге строится конус Г (Р), пересечение которого с гиперплоскостью {X |(P,X) = Ф} является прогнозом, основанным на гипотезе о рациональности поведения репрезентативного потребителя. Отметим, что если помимо гипотезы о рациональности поведения использовать предположение о выполнении Закона Спроса, то можно повысить точность прогноза. Модификация непараметрического метода с учётом Закона Спроса разработана в [27].

VIII. Обобщённый непараметрический метод

Погрешности, неизбежно существующие при формировании торговой статистики, могут служить источником нарушения условий рационализируемости. Вопрос о показателе, измеряющем степень рационализиремости торговой статистики, рассматривался в [17, 19, 24, 26].

Определение 3’. X Е Rm выявлено предпочтительнее с показателем ш > 0 Y Е Rmm (X У^ш Y), если выполняется неравенство (Р (X) ,X) > ш (Р (X) ,Y).

Если ш ^ 1 и X У^ш Y, то X У Y. В этом смысле выявленное предпочтение с показателем ш > 0 является обобщением понятия выявленного предпочтения.

Обобщенная сильная аксиома теории выявленного предпочтения с показателем ш  >  0. Если к  ^2

V1 Г-  mvn   v2  г-  mvn       ук  г-mm

^X Е       । ,  .^X      Е । ,   ..., -^X      Е। и X1  Уш  X2,  ..., Xк-1 Уш Xк, то

(Р (Xк) ,Xк) < ш (Р (Xк) ,X 1).

Заметим, что если выполнена обобщённая сильная аксиома теории выявленного предпочтения с показателем 1 ^ ш > 0, то выполнена сильная аксиома теории выявленного предпочтения.

Предложение 3". Пусть (Р(X) ,X) > 0 при любых X Е Rт\ {0} и выполнено условие отделимости (условие 2 теоремы 1). Для того чтобы для любого набора точек из множества

{XX0\X> 0 } U {XX1 \X> 0 } U

U {XXT\Х > 0} выполнялась обобщённая сильная аксиома теории выявленного предпочтения с показателем ш > 0, необходимо и достаточно, чтобы для любого упорядоченного набора {t 1, ..., tk} С T было справедливо неравенство

>

ш^к(Рt¹,Xt2^х) (Рt²,Xt3^х) ... (Ptk,Xt 1^х) ^

Если для любого упорядоченного набора {t 1, ..., tk} С T было справедливо неравенство шк (Рt1 ,Xt2х) Р3t2,Xt3х) ... Р3tk,Xt>

>

будем говорить, что торговая статистика {Рt,Xt}T₀удовлетворяет обобщённой однородной сильной аксиоме с показателем ш > 0.

Теорема 3 *. Следующие свойства торговой статистики эквивалентны:

• 1)    торговая статистика {Рt,Xt}T₀ удовлетворяет обобщённой однородной сильной аксиоме с показателем ш > 0, то есть для любого упорядоченного набора моментов времени {t 1, ..., t_k} С T выполняются неравенства

  >

  
  

  ш^к {Рt¹,Xt2^х) (Рt²,Xt3^х) ... Р^3tk,Xt 1) >

  
  

• 2)    существует решение (X₀, ..., XT) > 0 системы линейных неравенств:

шXт Р^тT,Xt¹) > Xt Р³t,Xt¹) (18)

Если утверждения теоремы 3’ выполняются с показателем 1 ^ ш > 0, то торговая статистика {Рt,Xt}T₀рационализируема в классе положительно однородных функций полезности с сильно выпуклыми поверхностями уровня (см. [22]).

Определение 6. Торговая статистика {Рt,Xt}T₀рационализируема с показателем рационализируемости ω , если система линейных неравенств (18) имеет положительное решение (X₀, ..., XT).

Идемпотентный аналог теоремы Фробениуса–Перрона [28]. Пусть A = ^aij IH?j=1 — квадратная матрица (n х n) с положительными элементами. Тогда существует вектор

X = (xi, ..., xn) с положительными компонентами такой, что шXi = max aijxj(i=1, ..., n)

IIC^I, где

(FtXt]

^Tt    (Fт Xt]^.

Это утверждение, по-видимому, впервые доказанное в [28], легко следует из теоремы Брауэра, примененной к непрерывному отображению стандартного симплекса

S =

|X = (x1, ..., xn) e Rn

в себя вида

yi =

n

E х- = 1

i=1

maxi^j ^n a-j xj 52n =1 maxi^j ^n akj Xj

Заметим, что предложение 5, которое позволяет прогнозировать структуру потребительского спроса, легко обобщается на случай гипотезы о рационализируемости торговой статистики с показателем ω (см. подробнее в [27]).

IX. Условия интегрируемости в неоклассической модели спроса

(i = 1, ..., n).

Число ш называется идемпотентным аналогом числа Фробениуса–Перрона матрицы A. Нетрудно показать, что система линейных неравенств

ωxi

>max aij^xj(i=i, ..., n)

имеет решения X = (x 1, ..., xn) с положительными компонентами тогда и только тогда, когда параметр ω не меньше, чем идемпотентный аналог ш числа Фробени-са — Перрона положительной матрицы A.

Определение 7. Пусть A = laij|||ⁿj=1 -квадратная матрица (n х n) с положительными элементами. Будем говорить, что матрица A является продуктивной в идемпотентном смысле, еслисуществу-ет вектор X = (x 1, ..., x_n) с положительными компонентами такой, что

Вопрос о содержательной интерпретации условий интегрируемости может быть проанализирован в терминах неоклассической модели потребительского спроса [29].

Предположим, что домашние хозяйства можно распределить по M социальным группам в соответствии со стереотипами их потребительского поведения. Стереотип поведения α-й группы будем описывать задачей о максимизации функции полезности u_a (X) e Ф1 при бюджетном ограничении. Обозначим через ^_a (F) совокупный доход α-й социальной группы в зависимости от цен²¹P . Индекс цен с точки зрения α-й группы определяется с помощью преобразования Янга:

qa (P) =

inf {xeRm |u_a

PX

(X) >0 } ua (X )

Xi > max aijXj(i=1,..., n).

В [29] показано, что дифференциальная форма суммарного спроса домашних хозяйств выражается в виде

Очевидно, что положительная матрица A является продуктивной в идемпотентном смысле тогда и только тогда, когда её идемпотентный аналог числа Фробениуса–Перрона не больше, чем единица.

Наименьшее значение ω , при котором система линейных неравенств (18) имеет положительное решение, характеризует степень нерационализирумости торговой статистики и является идемпотентным аналогом числа Фробениуса–Перрона (см. [24]) матрицы индексов цен Пааше

mM

” = E Xj (F) dFj = E XP) dqa (F) • j =1               a=1 qa

Предложение 6 [29]. Для того, чтобы существовала функция полезности F (X) e Ф1, рационализирующая суммарные функции спроса X (F) = (X 1 (F), •••, X_m (F)), то есть при F e int Rm выполнялось

X (F) e Argmax

{F(Y) (FY] <

²¹При изменении цен меняется стереотип потребительского поведения домашних хозяйств, происходит перераспределение их по социальным группам и изменяется совокупный доход социальных групп.

M

< ^Va (P) ,Y G Rm a =1

,

Предложение

^{Ф (q}i, ..., ^qM) ^{G Ф}1 •

7   [29]. Пусть

Тогда

необходимо и достаточно, чтобы существовала такая функция Ф (q 1, ..., q_M) G Ф₁, что функция Ф (q 1 (P), ..., q_M (P)) G Ф₁является преобразованием Янга F (X) и

^ 51(qi,

..., ^qM)

^, qi

.

.

.

⁵m⁽qi,

,

..

qM

., qM)^ _G

Va (P)    =        qa (P)_______x

E M=i vp ( p ) ф( q i ( p ),..., qM ( p ))

^{дф (}q¹,..., qM)

^x dq         Iq=q(p)^(a = ¹,..., ^M).

Для выполнения условий интегрируемости дифференциальной формы спроса ^ необходимо, чтобы распределение доходов по социальным группам зависело от цен косвенно через индексы цен с точки зрения разных социальных групп ⁽qi^(P),..., qM^(P)):

G Argmax{W(u_i, ..., u_M)|q_iu_i+ ... +

+qMuM ^ ¹,ui ^ 0, ..., uM ^ 0}, где

5a (qi, ..., qM) =

_        qa       дФ (qi, ..., qM)

Ф (qi, ..., qM)        dqa       ¹

(a = 1, ..., M);

2) для любого X G Rm индекс спроса F (X) не меньше, чем

max{W(ui(Xⁱ), ..., Um(X^M))|

Va (P)

E M=i ve ( p )

= 5a (qi (P),..., qM (P))

M

^Xa = X,Xi > 0, ..., XM > 0}, a=i причём равенство достигается при

X = (Xi, ..., Xm), где

M

Xj = E a=i

Va (P) dqa (P) qa (P) dPj

(j = 1,

..., m)

(a = 1, ..., M). То есть распределение доходов в обществе должно быть согласовано со сложившимися в обществе оценками уровня потребительских цен. В обществе должны действовать механизмы саморегулирования распределения доходов. В частности, рынки товаров не могут нормально функционировать, если нет рынка труда.

В рамках неоклассической модели потребительского поведения вопрос о выполнении условий интегрируемости для дифференциальной формы спроса ^ или дифференциальной формы обратных функций спроса ω сводится к анализу условий интегрируемости дифференциальной формы

E⁵a^(qi, ..., ^qM) ----------------dqa.      (19) a=i       ^qa

Рассмотрим преобразование Янга функции Ф (qi, ..., qM) G Ф1

M a=i qaua

W(ui, ..., Um) =

inf

{q 1>0. .... q_M ^01 Ф( q_i, Ф( q 1. .... q_M )>⁰}

..., ^qM)

где u_i, ..., u_M — значения функций полезности выделенных социальных групп.

для некоторого P G int Rm •

В политической экономии рассматриваются концепции справедливого распределения доходов в обществе. Формальное выражение такая концепция получает с помощью функции Бергсона, максимум которой реализуется именно на том распределении доходов, которое соответствует избранной концепции (см. [30]). Для существования индексов цен и спроса необходимо, чтобы распределение доходов между выделенными социальными группами соответствовало функции Бергсона W (u_i, ..., u_M) из предложения 7.

Функция Бергсона выражает компромисс экономических интересов социальных групп. Ее можно интерпретировать как политическую «партийную программу». Казалось бы, такую программу можно задавать непосредственно функциями распределения доходов 5a (qi, ..., qM) (a = 1, ..., M). Однако условия интегрируемости функций спроса обеспечивают лишь те функции распределения доходов, которые порождены какой-либо функцией Бергсона. «Партийная программа», которая не сохраняет условий интегрируемости, ведёт к дезорганизации экономической системы и не может счи- таться конструктивной.

Для выявления функции Бергсона, соответствующей сложившемуся в обществе компромиссу в распределении доходов, необходима бюджетная статистика {(Xt,a,Pt) \t = 0, ..., T; a = 1, ..., M}. Здесь P t — вектор цен в период времени t, Xt,α — вектор спроса α-й социальной группы в период времени t. Применим непараметрический метод построе- ния экономических индексов из раздела 7 к «торговой статистике» β-й социальной группы {(Xt,e,Pt) \t = 0, ..., T }. В результате построим индекс цены qe (P) с точки зрения β-й социальной группы. Положим (pt xt,e\ ute = 'q^pt) (в = 1, ..., M). Обозначим ut = (u1, ..., uM) ,qt = (qt, ..., qM). Применим к временным рядам {(ut,qt) \t = 0, ..., T}, рассматриваемым как торговая статистика, непараметрический метод. В результате в качестве «индекса спроса» получим функцию Бергсона. Отметим, что для изучения социальной структуры общества по данным бюджетной статистики можно использовать методы разработанные для анализа сегментации потребительского рынка.

X. Заключение

Рассмотрим теперь вопрос об интерпретации нарушения условий рационализиру-емости торговой статистики. С одной стороны, причиной нарушения могут быть погрешности в построении исходной торговой статистики. В этом случае непараметрический метод и лежащая в его основе теорема Африата–Вериана могут быть обобщены (см. [17,19,24,26]) за счёт введения в левую часть неравенств (14) дополнительного множителя ш > 1. Как отмечалось в разделе 8, наименьшее значение ω , при котором система линейных неравенств (14) имеет положительное решение, характеризует степень нерационализирумости торговой статистики и является идемпотентным аналогом числа Фробениуса–Перрона (см. [24]) матрицы индексов цен Паа-ше \\a,tУ, где Xt = (PtXЧ / (PтXЧ. Если это наименьшее значение в сравнении с элементами матрицы цен Пааше незначительно превышает единицу, то нарушение условий рационализируемости можно про- интерпретировать как следствие погрешностей в построении исходной торговой статистики.

С другой стороны, нарушение условий рационализируемости может быть следствием формирования новых потребностей и социальных отношений, например, как в случае со сменой технологических укладов после Великой экономической депрессии (см. [25], §3). В этом случае восходящая к В. Парето модель рационального репрезентативного потребителя оказывается неадекватной и должна быть заменена более общей моделью. Такая модель может быть построена на основе решения Э. Картаном задачи о приведении дифференциальной формы χ к наименьшему числу переменных с необходимостью учесть ограничения на то, чтобы замены переменных удовлетворяли априорным требованиям к экономическим индексам. Такого рода обобщения результатов Э. Картана иногда называют выпуклыми теоремами Дар-бу.

В рамках неоклассической модели спроса проблема интегрируемости функций спроса сведена к исследованию интегрируемости дифференциальной формы (19), построенной по функциям распределения доходов. Предположим, что функции

/51 (q 1, ..., qM) k q i

⁵m⁽qi,..., qM) q_M

)

являются трижды непрерывно дифференцируемыми, удовлетворяют закону Хикса и имеют обратные функции (r 1 (u 1, ..., Um), ..., rM (u 1, ..., Um)). В [31] показано, что существуют такие функции (Ф1 (q 1, ..., qM) , ..., Фk (q 1, ..., qM)) и (W1 (u 1, ..., Um), ..., Wk (u 1, ..., Um)) удовлетворяющие априорным требованиям к экономическим индексам, такие что в достаточно малой окрестности точек общего положения справедливы равенства

M x=E a=1

5a (q 1,..., qM) qα

dqa =

k

= У?Gs (^ф1 (q 1,..., qM),...,^фk (q 1,..., qM))^x s=1

xdФs (q 1, ..., qM),

M

• У^Га (u 1, ..., UM) dUa = a=1

k

• = ^2 Rs(Wi(ui, ..., um), ..., s =1

Wk(u 1, ..., UM))dWs(u 1, ..., UM).

Здесь k — класс дифференциальной формы χ в окрестности рассматриваемой точ^ки, ⁽G1 ^(Ф1, ...,^Фk) , ..., Gk^(Ф1, ...,^Фk)) и (R1 (W1, ..., Wk), ..., Rk (W1, ..., Wk)) системы функций удовлетворяют условиям отделимости и закону Хикса.

Система функций (W1 (u 1, ..., u_M), ..., Wk(u 1, ..., um)) является обобщением на неинтегрируемый случай функции Бергсона. Будем их интерпретировать как выработанные общественным сознанием «партийные программы» справедливого распределения доходов между социальными группами. Программы выражают интересы разных коалиций социальных групп. Число коалиций может быть разным, но не меньше класса дифференциальной формы. Это — наименьшее число противоборствующих интересов, которое может возникнуть в результате общественных компромиссов. Партийная борьба в обществе, если она приводит к объединению «партийных программ», объективно должна вести к сокращению их числа до класса дифференциальной формы. Системы функций ⁽^1 ⁽q 1, ..., qM) , ..., Фk⁽q 1, ..., ^qM)) и (W1 (u 1, ..., um), ..., Wk (u 1, ..., um)) определены не однозначно, поэтому ни одна из партий не в состоянии, вообще говоря, блокировать процесс объединения партийных программ.

Эмпирические исследования показывают, что в периоды структурной стабильности экономического развития условия интегрируемости выполняются. В это же время, как правило, социально-экономические программы различных партий оказываются близкими, что принято называть преемственностью политики. Напротив, в периоды структурной перестройки условия интегрируемости могут нарушаться, что приводит к ослаблению эффективности финансовых механизмов регулирования воспроизводства в экономике и кризисам. Одновременно с кризисами обостряется партийная борьба и изменяется партийная структура общества.

Для развития непараметрического метода и расширения возможности применения его в случае нарушения условий интегрируемости представляет интерес решение следующей задачи. Пусть задана торговая статистика {PtXt}^=₀, удовлетворяющая однородной слабой аксиоме теории выявленного предпочтения. Требуется конструктивно определить наименьшее значение класса дифференциальной формы обратных функций спроса ω для всевозможных продолжений данной торговой статистики до обратных функций спроса, определённых на всем Rm и удовлетворяющих условиям отделимости и однородной слабой аксиоме.

Работа выполнена при финансовой поддержке РФФИ (№ 08-07-00158 и № 09-01-13534 офи-ц), РГНФ (№ 08-02-00347), гранта Президента РФ по государственной поддержке ведущих научных школ (НШ-2982.2008.1), программы ПФИ ОМН РАН № 3, ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009-2013 годы (мероприятия 1.2.1, НК-15 П), ПФИ Президиум РАН П-2.