Проблемно-ориентированный программный комплекс для численного решения и исследования задач структурной биоинформатики с использованием методов стохастической оптимизации

Poluyan S., Ershov N. Problem-oriented software package for the numerical solution and research of structural bioinformatics problems using stochastic optimization methods. System Analysis in Science and Education, 2020;(4):37–47(In Russ). Available from: DOI: 10.37005/2071-96122020-4-37-47.

В работе представлен комплекс проблемно-ориентированных программ для проведения вычислительных экспериментов в двух задачах структурной биоинформатики: задаче предсказания пространственной структуры белка по аминокислотной последовательности и задаче предсказания оптимального состояния комплекса пептид-белок (пептид-белок докинг) при моделировании в полноатомном разрешении. В проводимых ранее исследованиях [1, 2] задачи рассматривались как задачи нелинейной непрерывной глобальной оптимизации. Для представления структур белка и комплекса, оценки энергии белка и взаимодействия пептида с белком в заданной пространственной конфигурации использовалось силовое поле Rosetta [3]. В качестве основных параметров при оптимизации выступают торсионные углы, которые при простейшей формулировке задач, являются свободными ротамерами, т.е. каждый параметр определяет полный угол в 360 градусов. Детальное описание задач и список оптимизируемых параметров представлены в работе [4].

В рамках проводимых исследований для нахождения глобального минимума путем оптимизации требуемых параметров ставилась задача применения стохастических эволюционных методов оптимизации. Для успешного применения методов оптимизации необходимо исключить из рассмотрения значения углов, которые приводят к физически невозможным пространственным конфигурациям. Для этого на каждый параметр требуется наложить ряд взаимозависимых ограничений, которые исключают определенный диапазон значений у каждого параметра. Поскольку для использования методов оптимизации в общем случае требуется непрерывное пространство поиска без ограничений, кроме границ поиска для каждого параметра, возникает проблема применения методов оптимизации. Чтобы разрешить указанную проблему, ранее был предложен подход с применением многомерного эмпирического квантильного преобразования, которое позволяет распределить значения параметров в требуемых диапазонах и свести пространство поиска для методов оптимизации в единичный непрерывный гиперкуб.

Принцип применения квантильного преобразования в рассматриваемых задачах практически одинаков, за исключением части оптимизируемых параметров. При этом предложенный подход по распределению значений параметров с помощью квантильного преобразования в общем виде никак не связан с рассматриваемыми задачами. В связи с вышеперечисленным, в рамках проводимых исследований разработана библиотека для выполнения многомерных квантильных преобразований, которая независимо использовалась при численном исследовании рассматриваемых задач с применением методов оптимизации.

Разработанный комплекс проблемно-ориентированных программ для численного решения и исследования задач структурной биоинформатики предоставляет функционал для проведения вычислительных экспериментов с использованием различных методов стохастической оптимизации. При этом в комплексе присутствуют две независимые программы-библиотеки: для задачи предсказания структуры белка и для пептид-белок докинга. При реализации комплекса использовалась разработанная библиотека для выполнения квантильного преобразования.

Основная цель настоящей статьи – раскрыть структуру и основной функционал библиотеки и комплекса. В первом разделе приводится описание библиотеки для выполнения квантильного преобразования и демонстрируются примеры, которые раскрывают принципы работы с предложенной библиотекой. В следующем разделе представлен функционал комплекса, приводятся примеры его использования и указываются основные варианты проведения исследований с его помощью. В заключении представляются результаты выполненной работы и указываются направления дальнейших исследований.

• 1.    Библиотека для квантильных преобразований

Для выполнения квантильных преобразований представлена библиотека, которой присвоено название mveqf с использованием аббревиатуры от словосочетания «многомерная эмпирическая квантильная функция». В рамках библиотеки представлена реализация многомерного эмпирического квантильного преобразования на основе дискретной выборки, сформированной на непрерывной области. Каждый элемент выборки представляется узлом регулярной сетки. Каждый узел сетки представляется набором целочисленных компонент. Принципы организации хранения выборки и процедура выполнения квантильного преобразования представлены в статье [1].

В библиотеке представлены четыре способа хранения выборки, которые могут быть использованы для последующего выполнения квантильного преобразования. Ниже представлен список структур данных, в которых пользователь может хранить выборку.

• 1.    Простой способ хранения, или просто явный. Заключается в хранении элементов выборки в таблице, т.е. представляет собой массив векторов, где каждый компонент вектора является либо вещественным значением, либо целочисленным компонентом узла, который может быть переведен в вещественное значение.

• 2.    Префиксное дерево, построенное с использованием целочисленных компонент узлов. Таким образом, ключами дерева являются векторы, представляющие собой узлы сетки. В библиотеке структура данных названа Trie .

• 3.    Модифицированное префиксное дерево TrieBased . Поскольку каждый узел представим одинаковым количеством компонент, т.е. длина любого ключа в дереве одинакова и значения последней компоненты любого узла ограничены размером сетки для текущей размерности, листья префиксного дерева можно объединить в один список. При этом происходит потеря контроля количества элементов на последнем уровне. Такой способ подходит для использования, когда каждый узел входит в выборку только один раз, т.е. с его помощью возможно только «равномерное» распределение. Указанный способ хранения выборки более компактный, чем при использовании обычного префиксного дерева, поскольку использование одного общего уровня существенно экономит память, при этом вычислительная сложность добавления узла полностью аналогична хранению в обычном префиксном дереве.

• 4.    Представление выборки с помощью минимального детерминированного конечного автомата (ДКА) возможно при использовании структуры данных MFSA . При отсутствии полной уникальности в компонентах добавляемых узлов, в префиксном дереве встречаются одинаковые и изоморфные поддеревья [5]. Их возможно исключить и перейти к ещё более компактному представлению выборки, чем при использовании модифицированного префиксного дерева. Для этого необходимо руководствоваться теми же принципами, которые лежат в основе перевода префиксного дерева в направленный ациклический граф. Указанный подход используется при хранении морфологических словарей.

Для реализации структуры данных MFSA с возможностью дальнейшего применения при преобразовании требуется использовать структуру узла, которая применяется в префиксных деревьях. Имеется в виду использование такого представления, где для каждого состояния хранятся исходящие из него ребра. Для поддержки минимального количества состояний в ДКА реализован инкрементный алгоритм [5], производящий минимизацию количества состояний после добавления каждого элемен- та. Теоретические оценки количества состояний ДКА при различных выборках и результаты реализованного в библиотеке алгоритма представлены в работе [1].

На рис. 1 приведена UML диаграмма основных классов библиотеки mveqf . Разработанные структуры данных для хранения выборки являются наследниками базового абстрактного класса Sample , в котором представлены различные операции для формирования выборки. На рисунке для класса Sample приведены только три основные операции: установка размерности ключа, добавление ключа в структуру и операция заполнения счетчика количества элементов, который указан в каждой вершине дерева (или в каждом состоянии в случае ДКА) и используется при преобразовании.

В перечисленных выше структурах данных различным образом реализована операция добавления insert . Операция set_dimension определяет длину используемых ключей, которые являются компонентами добавляемых узлов. Операция fill_tree_count определяет заполнение счетчиков в случае вхождения ключа один раз. Для всех структур данных, за исключением Trie , при добавлении узла, входящего в выборку более одного раза, принцип заполнения счетчиков идентичен и реализован рекурсивным обходом в глубину.

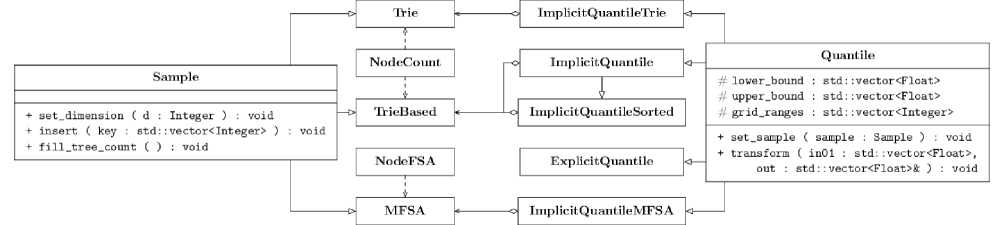
Рис. 1. UML диаграмма классов библиотеки mveqf

Вершины в структурах данных Trie и TrieBased реализованы с использованием класса NodeCount . Каждая вершина содержит список указателей на дочерние вершины, счетчик количества элементов и текущий компонент узла сетки. При формировании пространства поиска в задаче пеп-тид-белок докинга используется модифицированное префиксное дерево, созданное с помощью класса TrieBased , в котором содержатся потенциальные положений пептида, которые затем могут быть добавлены в основную выборку. В этом случае нет необходимости использовать структуру вершины со счетчиком, поэтому шаблон класса TrieBased позволяет указывать тип используемого узла. Например, в библиотеке представлен класс Node без счетчика.

Шаблоны классов Trie , TrieBased , MFSA требуют от пользователя указать конкретные типы данных, которыми должны представляться компоненты узлов сетки. Например, если максимальный размер сетки меньше 256, то нет необходимости использовать четырех байтовое представление узла сетки, а достаточно использовать беззнаковый тип std::uint8_t , который равен одному байту. В случае использования Trie и TrieBased в параметрах шаблона также указывается тип представления вершин дерева. Параметры шаблонов предоставляют пользователю возможность эффективно работать с памятью. Следует отметить, что тип счетчика не указан в параметрах шаблона, поскольку счетчик контролирует число узлов с одинаковым компонентом. Поэтому при использовании различных типов для хранения узлов результат преобразовании будет идентичный.

Для хранения списка указателей и последующего использования алгоритмов, представленных стандартной библиотекой шаблонов STL, реализован контейнер cst::vector, который представляет собой упрощенную версию включенного в STL контейнера std::vector. Реализация собственного последовательного контейнера заключается в необходимости минимизировать потребляемую память при хранении списка указателей на дочерние вершины. При работе с большими выборками высокой размерности в случае применения указанных структур в рассматриваемых задачах наблюдается низкая наполненность каждого уровня дерева [1], что ставит задачу минимизации требуемой для хранения вершины дерева памяти, которая решается с помощью использования реализованного контейнера. При этом должны быть сохранены принципы выполнения процедуры квантильного преобразования, которые включают использование стандартных алгоритмов STL. Представленный контейнер производит выделение памяти только под указатели на дочерние узлы. В отличие от контейнера std::vector, в котором при добавлении элемента резервируется дополнительная память, кон- тролируемая переменной capacity, содержащей объем зарезервированной для контейнера памяти, реализованный контейнер дополнительно хранит только количество элементов в контейнере. При этом в контейнере cst::vector сохранен функционал, который присутствует у последовательных контейнеров. Данный функционал требуется для работы с использованием стандартных алгоритмов STL.

Процедура многомерного эмпирического квантильного преобразования представлена в библиотеке классами, которые являются наследниками базового абстрактного класса Quantile. Для выполнения квантильного преобразования необходимы верхняя и нижняя границы, определяющие диапазон значений для каждого параметра, размеры регулярной сетки и выборка. Основными операциями класса являются добавление ранее сформированной выборки set_sample и выполнение квантильного преобразования transform , для которого указываются два вектора: вектор in01 входных значений, где каждый компонент принадлежит отрезку [0; 1], и вектор out преобразованных на основе предоставленной выборки значений. Операция добавления выборки в дочерних классах представлена в различных вариациях в зависимости от вида предоставляемой пользователем выборки.

В параметрах шаблонов классов пользователю необходимо указать тип данных с плавающей запятой, используемый для представления границ и при преобразовании, и целочисленный тип данных, используемый при хранении выборки и задания размеров сетки. В библиотеке представлены следующие пять шаблонов классов, в названии которых указано, какой вид преобразования и выборки используется. Отношение вида хранения выборки к классу представлено на рис. 1. Ниже приводится список классов.

• 1.    Класс ExplicitQuantile позволяет создавать объекты для выполнения преобразования при хранении выборки в явном виде, т.е. в виде таблицы векторов. Подходит для равномерного и неравномерного распределения.

• 2.    Класс ImpicitQuantileTrie поддерживает хранение выборки только в префиксном дереве. При преобразовании возможно равномерное и неравномерное распределение.

• 3.    Для объектов, созданных с помощью класса ImplicitQuantile , требуется выборка, представленная в модифицированном префиксном дереве TrieBased . Объекты этого класса могут использоваться только для равномерного распределения.

• 4.  Класс ImplicitQuantileSorted является наследником ImplicitQuantile. Выборка также представляет

• 5.    Объекты класса ImplicitQuantileMFSA используют выборку, которая представлена ДКА. Возможно использование только для равномерного распределения.

ся модифицированным префиксным деревом, но, перед проведением операции преобразования, все уровни дерева сортируются по возрастанию. Таким образом, возможно добиться уменьшения вычислительной сложности преобразования при достаточной наполненности каждого уровня [1].

Вычислительная сложность преобразования при использовании объектов классов ImpicitQuantileTrie , ImplicitQuantile и ImplicitQuantileMFSA идентична. Более подробно теоретические оценки сложности преобразования в зависимости от способа представления выборки приведены в работе [1].

На рис. 2 приведен пример формирования выборки и выполнения преобразования. Поскольку разработанная библиотека состоит только из шаблонов классов, т.е. является header-only library, для ее использования достаточно подключения соответствующих заголовочных файлов. Базовые классы и классы структур для хранения выборки представлены в одноименных файлах библиотеки. Для выполнения преобразования необходимо сформировать выборку, добавив в неё с помощью функции insert узлы соответствующей размерности и передать её в объект для квантильного преобразования, для которого требуется указать границы для каждого параметра и размеры сетки.

Реализованное в библиотеке квантильное преобразование может использоваться для аппроксимации распределения на основе известной плотности распределения вероятности. В библиотеке представлен функционал для ядерной оценки распределения по предоставленным точкам. При преобразовании используются соответствующие оценке интегральные функции, список которых представлен в библиотеке.

Выполнение эмпирического квантильного преобразования – частный случай решения транспортной задачи Монжа [6] в так называемом «полудискретном» варианте. В библиотеке представлен пример решения задачи Монжа для набора точек, выбранных из пространства Rn произвольным образом. Каждая точка входит в выборку один раз, это достигается подбором размеров сетки. Подбор размеров сетки может выполняться в двух вида. В первом случае путем последовательного увеличения размера сетки для каждой размерности. Во втором случае размер стеки увеличивается в два раза на каждом шаге для упрощения процедуры подбора. Процедура определения соответствующего точке узла сетки включает в себя использование алгоритма двоичного поиска. Таким образом, при размерности задачи d сложность определения составит O(d·log2 x), где x – количество узлов сетки. Шаг сетки изменяется, если при добавлении очередной точки в выборку в ней уже присутствует соответствующий точке узел. Затем формируется новая выборка пока все точки не получат уникальное представление в выборке. Поскольку вычислительная сложность преобразования логарифмическая, в зависимости от размеров сетки [1], малый шаг сетки существенно не влияет на сложность преобразования. Доступ к начальной точке определяется за константное время при условии хранения начальной выборки вещественных точек в хеш-таблице, где ключ – узел сетки, а значение – соответствующая точка из пространства Rn.

#include Cmveqf/implicit. h> // подключение библиотеки int main() { using gt = std::uint8_t; // тип для хранения компонентов узла сетки: char, int, ...

std::size_t d = 2; // размерность задачи std::vector<:size_t> grid = {9, 10}; // размеры сетки

// вид представления выборки - модифицированное префиксное дерево с вершинами NodeCount using sample_type = mveqf::TrieBased<:nodecount>, gt>;

// указатель на выборку, который затем передается в объект для квантильного преобразования std::shared_ptr sample = std::make_sharedО;

sample->set„dimension(d); // установка размерности sample->insert(std::vector{2, 6}); // добавление в выборку узла сетки sample->insert(std::vector{5, 7}); // первый компонент в отрезке [0;8], второй в [0;9]

std::vector lb(d, -3.0f); // нижняя граница для каждого параметра std::vector ub(d, 3.0f); // верхняя граница для каждого параметра mveqf::ImplicitQuantile mveqfuncQb, ub, grid); // объект для преобразования mveqfunc.set_sample_shared_and_fill_count(sample);          // передача выборки std::vector valuesOl = -[0.427f, 0.791f};  // значения для преобразования std::vector sampled(d);                   // вектор для хранения преобразования mveqfunc.transform(valuesOl, sampled); // выполнение квантильного преобразования }

Рис. 2. Пример использования библиотеки

Библиотека реализована на языке C++ и доступна в открытом доступе в репозитории сервиса GitHub [7]. В репозитории представлены различные примеры использования библиотеки, которые расположены в папке demos . Для сборки примеров можно воспользоваться кроссплатформенной системой автоматизации сборки CMake , используя представленный в репозитории файл CMakeLists . Проверка сборки проводились в операционной системе Windows, в среде разработки Microsoft Visual Studio , и в операционной системе Linux. Тестирование работы и отладка библиотеки проведены при помощи инструмента Valgrind с использованием компиляторов GNU GCC и Clang .

Проблемно-ориентированный программный комплекс

Реализованный программный комплекс представлен двумя независимыми библиотеками: для задачи предсказания структуры белка ( pepsgo ) и для пептид-белок докинга ( pepdockopt ). Обе библиотеки реализованы на С++ и после сборки могут быть подключены в пользовательский проект как разделяемые библиотеки. Предоставляемые библиотеками целевые функции могут применяться в вычислительных экспериментах с использованием различных методов стохастической оптимизации.

Например, при использовании данных комплексов проводились исследования [1, 2, 4] различных эволюционных алгоритмов глобальной оптимизации.

Предсказание структуры белка – предсказание по аминокислотной последовательности трёхмерной структуры белка, которое определяет нативное, т.е. функционально активное состояние. В качестве входного формата для представления последовательности выбран формат FASTA . В данном текстовом формате при помощи однобуквенных кодов последовательно обозначаются аминокислоты, составляющие цепочку белка. Аминокислоты, входящие в состав цепи белка называют остатками. Представленные библиотеки работают только с белковыми цепями, состоящими из двадцати стандартных аминокислотных остатков. Различные боковые группы остатков в составе главной цепи образуют боковые цепи. Пространственная структура белка определяется торсионными углами главной цепи (углы остатков φ / ψ / ω ) и углами боковых цепей. В качестве функции для вычисления энергии белка выступает предоставляемая пакетом Rosetta стандартная скоринг-функция.

Для предсказания структуры белка по указанной аминокислотной последовательности библиотека pepsgo поддерживает перечисленные ниже варианты формирования пространства поиска, которые определяют, какие углы будут добавлены в список оптимизируемых параметров и с какими ограничениями.

• 1.    Используются торсионные углы главной и боковых цепей без использования какой-либо дополнительной информации. Отклонение планарного угла ω главной цепи составляет 10 градусов.

• 2.    На углы главной цепи вводятся ограничения с использованием карт Рамачандрана, при этом используется квантильное преобразование. Ограничений на углы боковых цепей нет. Отклонение угла ω составляет 10 градусов.

• 3.    К ограничениям для углов главной цепи с использованием карт Рамачандрана и к отклонению угла ω вводятся дополнительные ограничения на углы боковых цепей с применением библиотеки Top500 [7], при этом также используется квантильное преобразование.

• 4.    Полностью аналогичен варианту под номером 3, но ограничения на углы боковых цепей вводятся с использованием библиотеки Dunbrack [8].

• 5.    Для углов главной цепи вводятся ограничения с использованием сгенерированного для последовательности файла с фрагментами средствами пакета Rosetta . Длина фрагментов может быть различной. Ограничения на углы боковых цепей вводятся с использованием библиотеки Dunbrack .

• 6.    В параметры добавляются только углы боковых цепей. Углы главной цепи фиксируются значениями предоставленной нативной структуры.

• 7.    Для углов главной цепи вводятся ограничения с использованием карт Рамачандрана. Углы боковых цепей фиксируются значениями предоставленной нативной структуры. Отклонение угла ω составляет 10 градусов.

• 8.    Полностью аналогичен варианту выше, но значения углов ω фиксируются на значениях, взятых из предоставленной структуры.

Предусмотрен также вариант под номером 0, при котором в параметры добавляются углы главной и боковых цепей без использования какой-либо дополнительной информации, за исключением угла ω , который фиксируется на планарном значении. Поскольку боковой радикал пролина замкнут в кольцо, углы боковой цепи пролина исключаются из списка параметров в случае выбора варианта под номером 1, 2, 6 или 0. Во всех случаях пространство поиска представляет из себя единичный гиперкуб, что достигается использованием, когда это необходимо, квантильного преобразования.

При создании комплекса и проведении экспериментов с указанными вариантами требуется передать в параметрах командой строки путь к базе данных Rosetta . Для вариантов под номерами 0, 1, 2 и 4 помимо включения пути к базе данных в параметрах требуется указать файл с последовательностью белка. В случае наличия нативной структуры в формате PDB [9] средствами библиотеки возможно вычисление среднеквадратичного отклонения, а также получение суперпозиции нативной структуры и структуры, получаемой указанным вектором из единичного гиперкуба. Для вариантов под номерами 6, 7 и 8 обязательно требуется нативная структура в формате PDB с последовательностью, которая идентична переданной для предсказания структуры белка.

Наиболее полно дополнительная информация используется при выборе варианта под номером 5, в котором пространство поиска формируется с использованием фрагментов. Фрагменты – короткие части известных белковых последовательностей, как правило, низкоэнергетические, которые выбираются протоколом fragment_picker пакета Rosetta в соответствии с данным предсказания вторичной структуры белка. В текстовой форме фрагмент представляет собой часть последовательности белка, в которой для каждого остатка приведены значения углов главной цепи. В случае комбинации фрагментов и рассмотрения структур, которые строятся с использованием значений углов фрагментов, возможно нахождение структуры белка, близкой к нативной.

Предсказание вторичной структуры белка, которое необходимо для генерации фрагментов, представляет собой информацию для каждого остатка белковой последовательности: к какой структуре относится остаток (спираль, лист или ни то, ни другое) и с какой вероятностью выполнено предсказание (от 0 до 9). Для использования протокола fragment_picker и генерации фрагментов указанной длины (обычно 3, 5 или 7 остатков) необходимо предоставить файл с предсказанием вторичной структуры в формате ss2 , который предоставляется программой PSIPRED [11]. Данный формат является унифицированным, поэтому возможно воспользоваться другими программами для предсказания вторичной структуры, часть из которых, как и PSIPRED , предоставляет возможность выполнить предсказание на веб-сервере по предоставленной последовательности в формате FASTA .

При формировании пространства поиска в варианте под номером 5 используется предсказание вторичной структуры в формате PSIPRED HFORMAT [11], который также генерируется при вторичном предсказании и представляет собой упрощенную запись предсказания. Вероятность предсказания в предоставленном файле определяет размер сетки для углов главной цепи остатка: чем она выше, тем меньше шаг сетки. Таким образом, для получения целевой функции и использования варианта под номером 5 требуются следующие входные файлы (в скобках приведены названия в соответствии с примерами, которые представлены в библиотеке):

• 1.    файл с последовательностью белка для предсказания (sequence.fasta);

• 2.    файл с фрагментами, длина фрагментов не фиксирована (fragments.Nmers);

• 3.    текстовый файл формата PSIPRED HFORMAT (prediction.horiz);

• 4.    текстовый файл, содержащий путь к файлу с нативной структурой в формате PDB (native.data).

На рис. 3 приведен пример использования библиотеки pepsgo и вычисления скоринг-значения в различных формулировках для представленных значений из пространства [0;1]^d , где d – размерность задачи. Во всех вариантах пространство поиска представляет из себя единичный гиперкуб.

Для подключения библиотеки необходимо подключить заголовочный файл, который содержит одноименный с библиотекой класс для создания объекта. Помимо этого, для работы с библиотекой необходимо использовать файл разделяемой библиотеки. После выбора одного из вышеперечисленных вариантов по предоставленной пользователем последовательности белка средствами библиотеки будут добавлены соответствующие параметры для оптимизации и сформировано пространство поиска. Функция библиотеки get_problem_dimension предоставляет пользователю размерность задачи. В библиотеке целевая функция представлена двумя вариантами: однокритериальным ( objective и objec-tive_mt ) и многокритериальным ( objective_mo и objective_mo_mt ). Функции могут быть использованы напрямую с помощью обращения к объекту библиотеки. Для удобства возможно создание независимого функционального объекта std::function с помощью связывателя std::bind с порядком задания свободных аргументов std::placeholders использование его как функции, как это сделано в примере на рис. 3.

Многокритериальный вариант функции разбивает результат вычисления скоринг-значения на два слагаемых (критерия). Первым слагаемым является энергия растворителя и электростатический терм. Вторым слагаемым являются все остальные энергетические термы. В сумме слагаемые дают начальное скоринг-значение, идентичное однокритериальному случаю. Для выполнения функции с отметкой mo в параметрах требуется передача вектора weights размерности d и вектора energies размера d+1 . Вектор weights содержит веса для линейной свёртки критериев, вектор energies – два вышеперечисленных слагаемых и их сумму. Результат вычисления функции – линейная свёртка критериев с использованием двух слагаемых. Вектор energies передается в функцию по ссылке, что позволяет после вычисления функции получить доступ к значениям слагаемых без весовых коэффициентов.

std::bind(&lt::objective_mt_mo, obj, „1, „2, „3, _4);

double res = f_mo_mt(valuesOl, 0, weights, energies); // линейная свертка с весами weights double elec_sol = energies[0]; // энергия растворителя и электростатического терма

// energies[1] - остальные термы за исключением elec_sol, energies[2] - полный score

}

Рис. 3. Пример использования комплекса

Функции с отметкой mt предоставляют пользователю возможность вычисления значения с указанием в параметрах номера потока. В отличии от функций без отметки они являются потокобезо-спасными и при вычислении по указанному вектору оперируют независимыми объектами.

Для выполнения пептид-белок докинга с использованием библиотеки pepdockopt в качестве основного входного параметра выступает пептид-белок комплекс в файле формата PDB . В роли пептида выступает последняя представленная в файле структура. В качестве целевой функции для оптимизации выступает энергия связывания белка и пептида, которая является единственным критерием при оптимизации. Библиотека предназначена для выполнения докинга в локальной области, при котором пептид связывается с белком в линейной конформации. Детали использования квантильного преобразования, которое позволяет производить докинг в локальной области места связывания, а также принципы формирования пространства поиска, представлены в работах [1, 2]. Пример использования библиотеки pepdockopt практически полностью аналогичен представленному на рис. 3, за исключением изменения названия заголовочного файла, подключаемой библиотеки и отсутствия предустановленных вариантов многокритериальной постановки задачи. Для углов боковых цепей белка и пептида используется библиотека Dunbrack .

Для сборки библиотек требуется полностью собранный пакет Rosetta [3], который свободно распространяется для академических целей. Для сборки пакета Rosetta требуется операционная система Linux/MacOS с компилятором GNU GCC или Clang с поддержкой стандарта С++11 . Полная сборка Rosetta под Windows не поддерживается [3]. Разработанные библиотеки тестировались только в операционной системе Linux .

Таким образом, для сборки и использования комплекса требуется:

• 1.    дистрибутив Linux и компилятор C++ с поддержкой OpenMP и стандарта С++11 ;

• 2.  библиотека для квантильных преобразований mveqf ;

• 3.    собранный стандартным путем пакет прикладных программ Rosetta и, в случае использования третьего варианта, библиотека Top500 . Библиотека Dunbrack поставляется с пакетом Rosetta .

Для сборки библиотек и прилагаемых примеров использования также требуется присутствие кроссплатформенной системы автоматизации сборки CMake . После загрузки соответствующего репозитория [7] необходимо изменить файл CMakeLists , указав в соответствующем месте путь к главной папке пакета Rosetta , компилятор, с помощью которого был собран пакет и его версия, а также путь к библиотеке mveqf . Затем, находясь в папке библиотеки, необходимо выполнить процедуру сборки библиотеки стандартными средствами CMake (команды для командной строки « cmake . » и « make »). В результате будет произведена сборка библиотеки и создан файл разделяемой библиотеки, который можно использовать. Помимо сборки библиотеки в папке bin будут сформированы исполняемые примеры использования, включая различные варианты предустановленных параметров.

Заключение

В результате выполненной работы разработана библиотека, с помощью которой возможно выполнять различные виды квантильного преобразования. Приведен список реализованных структур данных для хранения выборки и показан пример использования библиотеки. Представлен комплекс проблемно-ориентированных программ, который позволяет проводить исследования непрерывных однокритериальных и многокритериальных методов оптимизации на примере задач структурной биоинформатики. Продемонстрирован пример использования комплекса и приведены входные параметры для проведения экспериментов.

В разработанном комплексе пользователю представлена возможность проводить вычислительные эксперименты с использованием технологий параллельных вычислений при условии запуска на системах с общей памятью. Проверка применения параллельных вычислений проведена с использованием одного вычислительного узла кластера HybriLIT ОИЯИ [12, 13].

Целями дальнейшей работы является оптимизация реализованного инкрементного алгоритма построения минимального ДКА, а также полноценное документирование исходных текстов библиотеки и комплекса. В дальнейшем планируется регистрация представленной библиотеки и комплекса.