Проблемы группового преследования в линейной рекуррентной дифференциальной игре

i§ 1. Постановка задачи

В пространстве R^k (k ^ 2) рассматривается дифференциальная игра Г n + m лиц: n преследователей Pi,... ,P_n и m убегающих E\,..., E_m [1-7]. Закон движения каждого из преследователей Pi имеет вид

Xi = A(t)xi + Ui, Xi(to) = x⁰, щ € V.

Закон движения каждого из убегающих Ej имеет вид yj = A(t)yj + Vj, yj (to) = yj Vj e V, где Xi, yj, Ui, Vj € Rk, A(t) — непрерывная матричная функция, V — строго выпуклый компакт с гладкой границей, zj = x0 — y0.

П р е д п о л о ж е н и е 1. Фундаментальная матрица Ф^) системы w = A(t)w, Ф(^) = E является рекуррентной на [to, то), а <^(t) равномерно ограничена на [to, то).

• §    2. Поимка одного убегающего

Пусть m = 1, преследователи используют квазистратегии, условие поимки убегающего — х р (т ) — yi(r) € M p при некоторых p, т, где Mi, . . ., M n — заданные выпуклые компакты, причем х0 — у0 € M_i для всех i.

Т е о р е м а 1. Пусть выполнено предположение 1 и y°° € Intco{x⁰ — Mi, ... ,x^ l — M n }. Тогда в игре Г происходит поимка.

• §3 . Поимка скоординированных убегающих

Предполагается, что все убегающие используют одно и то же управление. Цель группы преследователей — поймать хотя бы одного убегающего, условие поимки убегающего — х_р(т ) = y_q(т ) при некоторых p, q, T, причем z⁰j = 0.

Т е о р е м а 2 . Пусть выполнено предположение 1 и

Intco{x°, . . .,x°n]n co{y°, ...,y° m } = 0. (1)

Тогда в игре Г происходит поимка. С л е д с т в и е 1 (см. [4]). Пусть A(t) = 0 для всех t ^ 0, V = Di( 0) и выполнено условие (1). Тогда в игре Г происходит поимка.

П р и м е р 1 . Пусть k = 2, to =0, матрица A(t) имеет вид

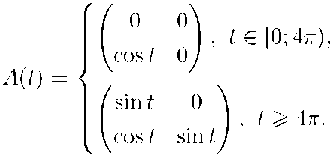
Тогда фундаментальная матрица Ф(t) имеет вид

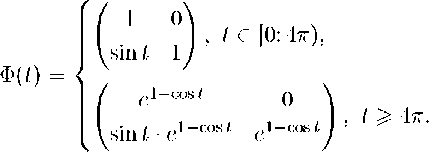
Матрица Ф(Ь) является рекуррентной.

У т в е р ж д е н и е 1 . Пусть выполнено условие (1). Тогда в игре Г происходит поимка.