Проблемы обеспечения оперативного мониторинга полета наноспутника при попутном запуске с орбитальной ступени РН “Союз”

лены следующие значения угловой скорости орбитальной ступени в проекциях на оси связанной системы координат (с учетом погрешностей системы управления) в момент времени, соответствующий разделению полезной нагрузки (ПН) и орбитальной ступени:

to x = - (2,5 ± 0,3) град/с,

® y = ^(0,0 ± ^2,5) град/с, (1) to z = (0,0 ± 2,5) град/с.

Здесь отклонения компонентов вектора угловой скорости от средних значений приведены в предположении о нормальном законе распределения соответствующих случайных величин, а сами отклонения вычислены как утроенное значение стандартного отклонения.

По штатной циклограмме работы РН “Союз” через 0,7 с после отделения ПН от орбитальной ступени включается реактивное сопло, создающее дополнительную силу, закручивающую и уводящую орбитальную ступень от ПН. Рассматривается случай, когда с целью отделения наноспутника происходит задержка включения реактивного сопла, обеспечивающая безопасность относительного движения орбитальной ступени, основной полезной нагрузки и наноспутника.

Возможности решения навигационно-связных задач в случае, если наноспутник не имеет собственной системы ориентации и стабилизации, зависит от характера его неуправляемого движения относительно цента масс после отделения от орбитальной ступени. Принимается, что отклонения компонентов вектора угловой скорости от средних значений для наноспутника за счет погрешности срабатывания собственной системы отделения увеличиваются не более чем в два раза и составляют:

to x = - (2,5 ± 0,6) град/с , ^юу = ^(0,0 ± ⁵⁾ град/с ,        (2)

to z = (0,0 ± 5) град/с.

В результате наноспутник получает некоторый импульс и приобретает начальный кинетический момент. На начальном этапе движения можно пренебречь действием внешних сил на динамику движения. Предполагается, что наноспутник является динамически симметричным твердым телом (моменты инерции относительно поперечных осей равны между собой I y = I z = I n ). В этом случае его вращательное движение представляет собой регулярную прецессию, при которой продольная ось, проходящая через центр масс, описывает круговой конус относительно неизменного в пространстве направления вектора кинетического момента K ₀ (угол полураствора этого конуса обозначен a k ). Движение оси симметрии вокруг вектора кинетического момента K ₀ происходит с постоянной угловой скоростью прецессии / & . Одновременно наноспутник вращается с постоянной угловой скоростью собственного вращения р вокруг продольной оси симметрии (рис. 1).

Значения угла полураствора конуса прецессии a k , скорости прецессии / и скорости собственного вращения р определяются по формулам [2]:

где K 0 = -^ K x ₀ + K n ₀ — модуль кинетического мо

мента; K x 0 = I x ^ x 0 , K n 0 = I n to ,0 ^- продольная ^и поперечная составляющие кинетического момента; I_x – продольный момент инерции наноспут-

ника; to x ₀ , to n ₀ = J to y ₀ + to z ₀ - продольная и поперечная составляющие угловой скорости.

Предположим, что компоненты поперечной составляющей угловой скорости независимы и распределены по нормальному закону с нулевыми математическими ожиданиями и дисперсиями, равными O y = O z = о . Разбросом величины продольной угловой скорости to x ₀ будем пренебрегать. Тогда, вычисляя распределение функции по распределению аргумента в соответствии с [3], получим аналитические выражения для плотности распределения угла полураствора конуса прецессии a k е [ 0, п /2 ] :

f (ak ) =

Kx0(tgak + tg "ak ) InO2

exp -

V

^^^^^^^B

^{( K}x 0 tg ^a k ⁾²

2 In O ²    )

и плотности распределения угловой скорости

прецессии: / е

да

a k = arctan

( К Л Kn 0

UKxd J

•

f ^{( /} ) = - ^ yexP о

(-(IO-K^ ) 2120-2

V     ² I n^O       J

.

K

/ = —⁰

I n ,

■ р =

( I n - I x )

I n

I ^tox 0I

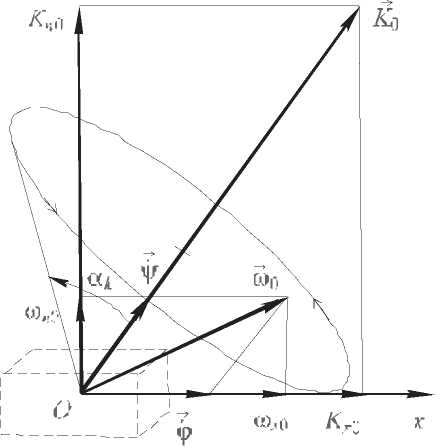
Рис. 1. Регулярная прецессия наноспутника

Для определения статистических характеристик распределения случайных величин, входящих в модель прецессионного движения - угла полураствора конуса прецессии a _k , скорости прецессии / , скорости собственного вращения р -было проведено статистическое моделирование по соотношениям (3) в предположении нормального закона распределения компонент вектора угловой скорости с использованием приведённых значений их моментных характеристик (2). Объём сформированной выборки реализаций составил 10000 численных экспериментов, что соответствует погрешности получаемых оценок около 1%. При этом продольный и поперечный моменты инерции наноспутника моделировались как случайные величины с равномерными законами распределения на предельных интервалах изменения их величин ± 15 %.

На рис. 2 показаны графики для эмпирической модели плотности распределения угла полураствора конуса прецессии наноспутника a _k и полученной аналитической модели (4), где величины продольного и поперечного моментов инерции принимались равными их средним значениям.

На рис. 3 приведено сравнение эмпирической модели плотности распределения скорости

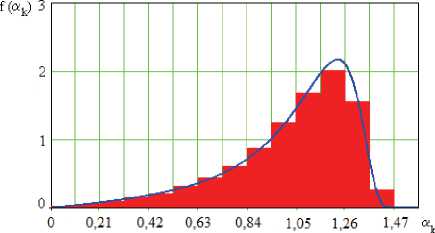
Рис. 2. Плотность распределения угла полураствора конуса прецессии наноспутника

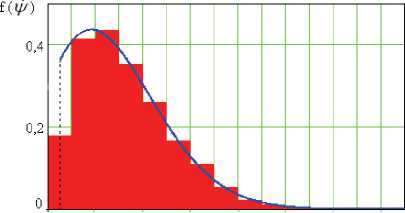
0,75 1,75   2,75   3,75   4,75   5,75   6,75   7,75 1^,град/с

В табл. 1 приведены средние значения и среднеквадратические отклонения угла полураствора конуса прецессии α _k , скорости прецессии ψ & , скорости собственного вращения ϕ & , полученные в результате статистического моделирования, и математические ожидания и среднеквадратические отклонения этих величин, вычисленные с использованием выражений (4) и (5).

Как видно из приведённых результатов, значения статистических характеристики, полученных в результате статистического моделирования и вычисленных с использованием соотношений (4) и (5), практически совпадают. Это подтверждает допустимость сделанных предположений и возможность использования полученных аналитических законов распределения (4) и (5) для анализа углового движения орбитальной ступени.

Поскольку продольная ось наноспутника прецессирует относительно вектора кинетического момента, то угол конуса постоянного обзора радиоаппаратуры, формирующегося за виток прецессии орбитальной ступени, определяется как δ _c = δ - 2 α _k (рис. 4), где δ угол конуса обзора радиоаппаратуры (угол диаграммы направленности фазового центра антенны).

Для анализа возможности решения навигационно-связных задач на наноспутнике, совершающем неуправляемое движение в соответствии с полученными выше вероятностными моделями, принимается, что вектор кинетического момента наноспутника лежит в плоскости, проходящей через вектор скорости, и её положение задается углом γ, значения которого принимаются случайными и распределенными равномерно в интервале от 0 до 2 π .

Введены следующие определения:

• -    под “полной” задачей навигации понимается задача определения положения наноспутника в пространстве (три геоцентрические координаты x,y,z ) и времени t . Решение данной задачи возможно при условии непрерывной видимости од-

• Рис. 4. Угол диаграммы направленности фазового центра антенны

Таблица 1. Статистические характеристики распределения

Величи на Расчет Угол полурас твора конуса прецессии Скорость прец ессии Скорость собственного вращения αk , град σ , град αk ψ& , град/с σψ& , град/с ϕ& , град/с σϕ& , град/с Ста тистическое моделиро ва ние 59,0 15,0 2,38 0,95 1,50 0,17 С использованием формул (4) и (5) 59,0 14,8 2,37 0,97 1,50 0 ной и той же группировки навигационных спутников (НС), числом не менее четырёх;

- под “ограниченной” задачей навигации по- нимается задача определения только положения наноспутника в пространстве. Решение данной задачи возможно при условии непрерывной видимости одной и той же группировки из трёх НС;

• -    под “горячим”, “тёплым” и “холодным” стар-

• том понимается первое решение задачи после включения навигационного приемника при длительности интервала видимости одной и той же группировки НС не менее 30, 90 и 180 секунд, соответственно.

При анализе возможности передачи данных через низковысотную систему связи Глобалстар рассматриваются продолжительности сеансов связи не менее 5 минут и не менее 10 минут в зависимости от требуемого объёма передачи данных.

Исследование возможности решения задач навигации и связи при условии неориентированного полёта наноспутника проводилось на модельной задаче при следующих исходных данных:

• -    орбита наноспутника околокруговая со средней высотой 220 км, долгота восходящего узла Q = 97 ° , наклонение орбиты i = 51 ° ;

• -    орбитальная структура спутниковых радионавигационных систем ГЛОНАСС и GPS соответствовала дате 16.04.2012 (рис. 5);

• -    орбитальная структура низковысотной системы связи Глобалстар соответствовала дате 16.04.2012;

• -    ориентация вектора фазового центра антенны задается углами α _k , γ . Значения угла α _k принимаются в соответствии с теоретическим законом плотности распределения, описываемым формулой (4), а угол γ перебирался в диапазоне значений от 0° до 360° с шагом в 10°;

• -    вектор фазового центра антенны ориентирован вдоль продольной оси наноспутника;

• -    ширина диаграмм направленности навигационной и связной антенн постоянна и равна 180°;

• -    интервал времени, на котором исследуется

возможность решения задачи навигации и связи, равен периоду движения наноспутника по орбите.

Для расчета вероятности возможности решения навигационных и связных задач использовалась формула полной вероятности [3]:

P ( A s ) = T P ( A s I » *( » C ) ,

i = 1

где P(As | 5C) - условная вероятность решения навигационной задачи (s=1) или сеанса связи (s=2), при условии реализации угла §c , P(^c') - вероятность появления реализации величины угла полураствора конуса прецессии δc .

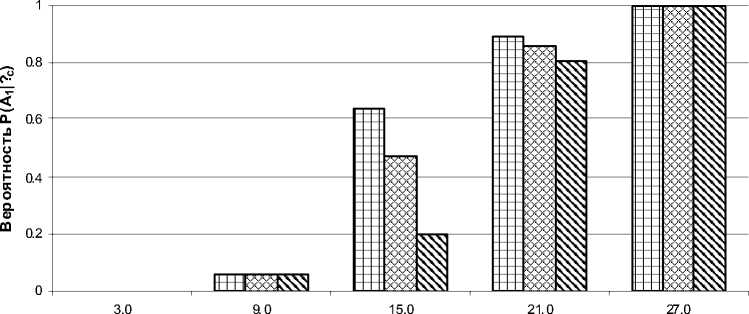
На рис. 6 представлены условные вероятности P(A1 | 5*c) характеризующие возможности решения “полной” задачи навигации при различных значениях угла δc , а на рис. 7 представлены вероятности возможности решения “полной” и “ограниченной” задач навигации при “горячем”, “теплом” и “холодном” стартах. Как следует из рис.7, вероятность невозможности определения положения наноспутника в пространстве (на периоде движения наноспутника по орбите) P(A1) равна 0,12.

На рис. 8 представлены условные вероятности возможности проведения сеанса связи P ( A 2 | 5‘_c ) длительностью не менее 5 и 10 мин при различных значениях угла δ _c . Соответствующие значения вероятности возможности проведения сеанса связи через спутники Глобалстар составляют, соответственно, 0,82 и 0,71 на периоде движения наноспутника по орбите.

Таким образом, использование современных навигационных и связных спутниковых технологий позволит с вероятностью не менее 0,82 обеспечить оперативный автономный мониторинг движения наноспутника при его неориентиро-

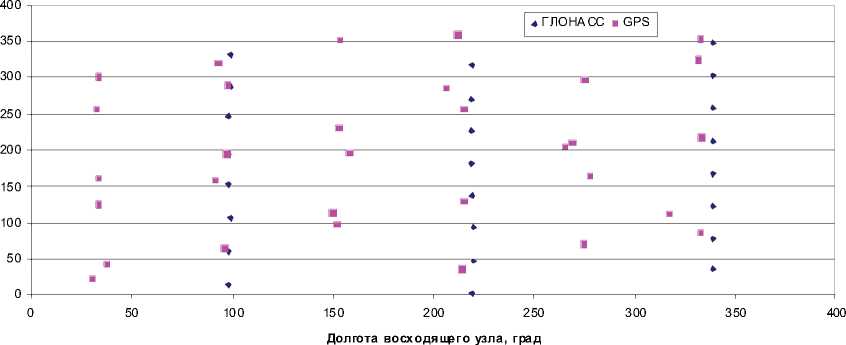
Рис. 5. Положения навигационных спутников на опорную дату задания эфемерид

Угол , град ^c , град

“горя чий” старт         “теплый” старт          “холодный” старт

Рис. 6. Условные вероятности решения “полной” задачи навигации при различных углах δ _c

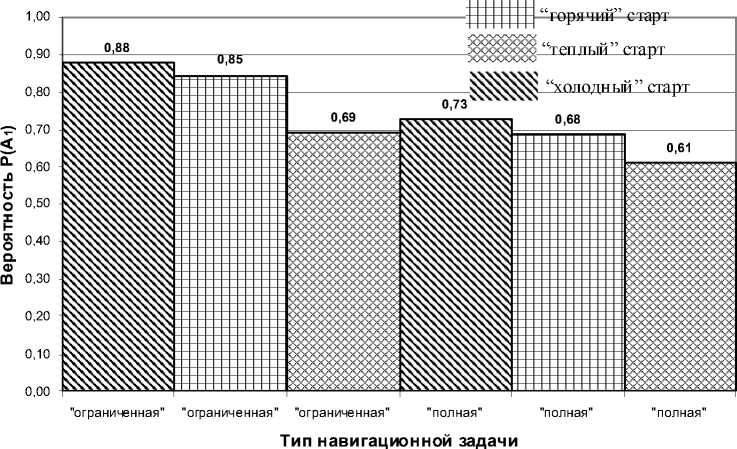
Рис. 7. Вероятности решения задач навигации (h=220 км)

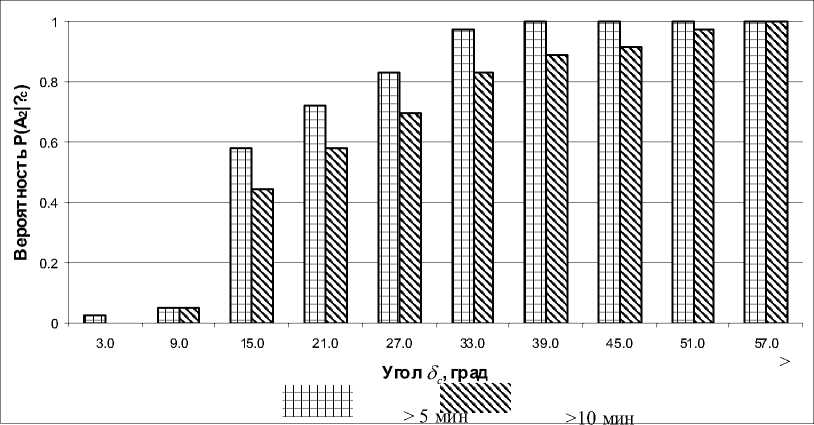
Рис. 8. Условные вероятности сеанса связи при различных углах δ

ванном полёте в случае попутного запуска с орбитальной ступени ракеты-носителя “Союз”.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 11-08-00644 а.