Проблемы применения многослойного персептрона при прогнозировании банкротства компаний

Проблема банкротства родилась с развитием рыночных отношений. Особый интерес к методам прогнозирования банкротства возник со второй половины XIX века, после Великой депрессии. Именно в те времена появились популярные в наше время модели математического дискриминантного анализа, однако до сих пор остаётся проблема точного прогнозирования.

Экономика России до сих пор не оправилась от кризиса. Так, опираясь на доклад Центра макроэкономического анализа и краткосрочного прогнозирования от первого квартала 2019 года, можно говорить об относительном сохранении числа банкротств по сравнению с кризисными 20142015 годами.

Перспективным направлением развития методов прогнозирования банкротств является нейросетевое моделирование. С развитием вычислительных мощностей использование нейросетей стало более доступным. Целью данной работы является анализ проблем применения многослойного персептрона при прогнозировании банкротства компаний.

Исходя из классификации Хайдарши-ной Г.А. (2007), нейросетевое моделирование занимает особое место в рамках количественных методов оценки риска банкротства компаний [1]. Оно находится на стыке информатики, математики, философии и биологии. Этот класс аналитических методов построен на принципах функцио- нирования мозга, в частности, нейросети приобретают знания в процессе обучения, для хранения информации используются веса межнейронных соединений.

Данный подход - один из типичных примеров нетеоретического исследования, он представляет собой так называемый «черный ящик», поэтому главное, на чем стоит сосредоточиться - точность прогнозов и их прикладная ценность. Нейронные сети наиболее эффективны, когда формализация решения проблемы невозможна или неэффективна [1].

К объективным достоинствам нейронных сетей следует отнести: их нелинейную природу, позволяющую решать задачи с высокой точностью, относительную простоту в использовании, способность не учитывать несущественные факторы, универсальность, устойчивость к шумам [2, 3]. К недостаткам нейросетевого моделирования относятся:

• -    необходимость регуляризации (повышения устойчивости прогнозной силы) и предобработки данных, которые, в то же время, малоисследованны [2];

• -    невозможность теоретически обосновать полученный прогноз.

Первым, с чем придётся столкнуть аналитику, желающему применить нейросетевое моделирование в своем анализе, является вопрос выбора вида нейронной сети. К наиболее популярным видам относятся: многослойный персептрон, радиальная ба- зисная функция, вероятностная нейронная сеть, линейная сеть. Критерием популярности, в данном случае, является их относительно доступная для широкого пользователя реализация, в частности, в программном продукте STATISTICA. В тоже время, способностью к экстраполяции вкупе с возможностью относительно быстро решать нелинейные задачи обладают только многослойные персептроны, а поскольку зачастую важна оперативность решений, и экстраполяция данных в условиях ограниченности выборки необходима, целесообразнее всего именно их использование [4].

Одна из вариаций многослойного персептрона представлена на рисунке.

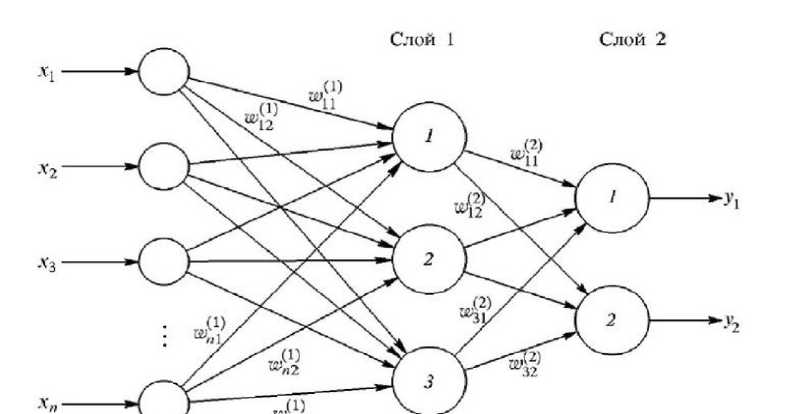
Рисунок. Схема двухслойного персептрона с 3 нейронами в скрытом слое, двумя нейронами в выходном слое и n входами

Примечание: x n обозначает n-ый вход; (У n1 , (У n2 и (У n3 обозначают веса от n-ого входа к 1, 2 и 3 нейрону на скрытом слое соответственно; (У 11 , (У 12 , (У 31 , (У 32 обозначают веса от 1,3 нейрона на скрытом слое к 1, 2 нейрону на выходном слое соответственно; y 1 , y 2 обозначают выходные значения.

При работе многослойного персептрона на вход подаются данные, впоследствии они переходят далее промежуточным и выходным нейронам, после обработки которыми сеть выдаёт результат. Каждый нейрон вычисляет сумму взвешенных по весам выходов предыдущего слоя, так называемое значение активации. В классическом случае, в последующем он вычитает из неё пороговое значение и преобразует получившееся значение с помощью функции активации.

Существует несколько алгоритмов обучения нейронной сети. Наиболее известный – алгоритм обратного распространения. При этом вычисляется вектор гради- ента поверхности ошибок. Он указывает направление кратчайшего спуска по поверхности из данной точки, поэтому если «продвинуться» по нему, ошибка уменьшится. Последовательность таких шагов в итоге приводит к нахождению минимума того или иного типа.

После выбора вида используемой нейронной сети необходимо решить следующие вопросы [5]:

• 1)    определение набора исследуемых показателей;

• 2)    сбор данных, формирование обучающей и тестовой выборки;

• 3)    предобработка данных;

• 4)    конструирование и обучение сети;

• 5)    диагностика сети.

Часто бывает сложно установить, какие именно показатели несут в себе полезную информацию, в то же время, многослойные персептроны устойчивы к подаче на входы данных, не имеющих пользы [2]. Опираясь на вышесказанное, на вход нейронной сети рекомендуется подавать все показатели, но при условии выполнения эвристического правила, согласно которому величина выборки должна быть в 10 раз больше числа параметров нейронной сети [3].

Число параметров нейронной сети для двуслойного персептрона вычисляется по формуле 1.

N = (A + С) * B,          (1)

где A – число входных признаков;

B – число нейронов на скрытом слое;

C – число выходных нейронов.

В случае, если данное правило не выполняется, возникает риск «проклятия размерности», а значит возникает проблема определения набора исследуемых показателей. Действительно, каждый дополнительный входной нейрон увеличивает размерность в пространстве данных. Очевидно, что для «заселения» такого простран- ства достаточно плотно, чтобы можно было «увидеть» структуру данных, требуется всё больше точек. Многослойный персептрон в меньшей степени, чем иные нейронные сети страдает от «проклятия размерности», поскольку способен, к примеру, занулять все веса, идущие от «бесполезного» входного нейрона. Тем не менее, точность многослойного персептрона возможно значительно улучшить, исключив показатели, не несущие или несущие мало полезной информации [4].

Некоторые авторы для этого рекомендуют выбирать показатели интуитивно [3]. Иные предлагают математические подходы к решению этой проблемы, среди них может быть использован отбор по мультиколлинеарности, а также метод главных компонент, факторный анализ и многомерное шкалирование. Сравнительный анализ последних приведен в таблице 1 [4, 5].

Таблица 1. Сравнительная характеристика некоторых методов понижения размерности

Критерии оценки	Методы снижения размерности
	МГК	ФА	МНШ
Сложность  реализа ции	Средняя	Высокая	Средняя
Точность анализа	Высокая	Очень высокая	Выше среднего
Распространенность	Очень высокая	Высокая	Высокая
Спектр охвата задач	Очень широкий	Широкий	Очень широкий
Смысловая нацеленность критерия информативности	Максимизация содержащейся в z(1), …, z(p’) доли суммарной вариабельности исходных признаков х(1), … х(p).	Максимизация точности воспроизведения корреляционных связей между исходными признаками по их аппроксимациям с помощью вспомогательных переменных z(1), …, z(p’)	Приписывание каждому объекту значений условных координат таким образом z(1), … z(p), чтобы по ним максимально точно восстанавливалась структура парных описательных отношений между объектами.
Нормальное распределение данных	Нет	Да	Нет

Как видим из таблицы, факторный анализ даёт самую высокую точность при отборе наиболее важных показателей, однако предъявляет достаточно жёсткое условие о нормальном распределении данных. Метод главных компонент же при сравнимой с многомерным шкалированием сложностью реализации, даёт точность выше последнего. Однако, поскольку метод главных компонент является чисто линейным методом, он может не учитывать некоторые важные характеристики структуры данных [4].

Принципиально иной способ понижения размерности связан с использованием вероятностных нейронных сетей [4]. Данный метод опирается на их уязвимость к плохим данным, исходящей из невозможности подобно сетям на линейных элементах занулять бесполезные переменные. Так, перебрав характеризующие выборку переменные, возможно достичь такого набора показателей, при котором вероятно- стные нейронные сети дали бы наилучший результат, что свидетельствовало бы о его оптимальности.

Другой проблемой является сбор данных. Необходимо, чтобы численность выборки была больше числа параметров минимум в 10 раз, а сама выборка была представительна. Основными источниками информации о финансовом состоянии организаций являются такие информационноаналитические агентства, как Bloomberg, TR Eikon, FIRA PRO, СПАРК, а также агентства, уполномоченные на опубликование информации об эмитентах, например, «Система комплексного раскрытия информации «СКРИН», «Интерфакс». Нельзя не отметить, что помимо обучающей выборки, на которой сеть будет обучаться, необходима тестовая выборка – если её не ввести, нейросеть начинает переобучаться [6].

Предобработка данных заключается в приведении данных к интервалу [0;1] или [-1;1]. Причина этого напрямую связана с функцией активации: к примеру, если в нейроны с сигмоидальной функцией активации будут подаваться большие значения, нейронная сеть не сможет их «воспринимать». Наиболее популярные функции активации с их границами чувствительности приведены в таблице 2. В случае с традиционно выделяемыми функциями активации, в границы чувствительности любых будет входить интервал (0;1), следовательно, он является условно универсальным, а значит преобразовывать свои данные перед загрузкой в нейронную сеть на случай возможного изменения используемой функции активации стоит так, чтобы они входили в него [7].

Таблица 2. Распространённые виды функций активации

Тип функции активации	Формула	Границы чувствительности
Биполярная	1 при  ≥0 f W =  1       п -1 при <0	[-1;1]
Линейная	f (X) = X	(-ш;+ш)
Логистическая сигмоида	1 ()=      , 1+у где а - параметр наклона сигмоидальной функции акти вации	(0,1)
Гиперболический тангенс	1- f (x) = tanh(2) = 1 + e _,, где - параметр наклона сигмоидальной функции активации	(-1,1)
Экспоненциальная	f(x) = е - х	(0; +™)
Синусоидальная	f (х) = sin (x)	[-1;1]

Также в задачах классификации предобработка данных подразумевает работу с кодировкой номинальных переменных. Номинальные переменные, в зависимости от числа различающихся значений, могут быть двузначными и многозначными. Если двузначные достаточно просто закодировать, поставив в соответствие одному из классов единицу, а другому ноль, то с многозначными возникают трудности. Будет ошибочным кодировать номинальную переменную с классами в порядковой шкале, к примеру, слон, человек, машина, как 0, 1, 2, потому что человек будет являться нечто средним между машиной и слоном. Здесь используется метод 1-из-N. Так, правильным решением здесь будет для слона (1;0;0), для человека (0;1;0), для машины (0;0;1). Вопрос конструирование многослойного персептрона в первую очередь связан с количеством слоёв и числом нейронов на скрытых слоях. Двухслойный персептрон подходит для решения широкого круга задач, поэтому обычно используют один скрытый слой [5].

Если взять слишком большое число нейронов, то сеть может переобучиться, её точность на практике будет слишком мала. Если взять слишком маленькое число нейронов, то нейросети может не хватить ги- перплоскостей для точного разграничения классов. Не обязательно оптимальным решением для повышения точности на практике будет и взятие максимально возможного числа нейронов при соблюдении эвристического правила, при котором выборка была больше числа параметров нейросети в 10 раз, поскольку уменьшение нейронов до определённого предела может улучшать способности сети к обобщению [8].

К тому же, необходимо выбрать и функции ошибки, функции активации нейронов на скрытом и выходном слоях, метод обучения. Зачастую эти проблемы решаются методом ручного перебора [3].

Также необходимо выбрать алгоритм обучения. Наиболее популярны градиентный спуск, метод сопряжённых векторов, алгоритм Бройдена-Флетчера-Гольдфарба-Шанно. Однако их всех объединяет постепенный спуск по той или иной плоскости ошибки, при этом нужно задать шаг обучения - на какую величину этот спуск будет происходить.

Другим выбором, перед которым придётся столкнуться использующему нейронные сети, является функция ошибки. Первым распространенным видом является функция квадратов разности результата с истинным значением, вторым - кроссэнтропия. Она рассчитывается по формуле 2.

/ = -1 * log(y) + (1 - t) * log (1 - у), (2)

где t - целевая переменная; у - предсказанное значение.

Обязательно также и тестирование сети, для чего используются валидационные выборки. Действительно, может случиться так, что пусть нейронная сеть и показывает достаточно высокие результаты как на тестируемой выборке, так и на учебной выборке, эти результаты в реальных условиях могут быть гораздо хуже, потому что потенциально может произошёл некий случайный подбор. Валидационная выборка служит для того, чтобы избежать этого, в неё включаются такие объекты, на которых НС не обучалась и не тестировалась ранее.

Таким образом, были проанализированы основные проблемы при использовании многослойного персептрона в прогнозировании банкротства компаний - выбор вида нейронной сети, определение набора исследуемых показателей, сбор данных, формирование выборки, предобработка данных, конструирование, диагностика и обучение сети. Оптимальным выбором при прогнозировании банкротства и одним из наиболее популярных видов нейронных сетей является многослойный персептрон.

При определении используемых показателей необходимо отсекать те, что не несут полезной информации. Для этого возможно использовать как экспертный отбор, так и определенные математические методы. Отдельно стоить выделить использование вероятностных нейросетей -подбирая содержание набора подаваемых признаков, можно выделить такой состав, при котором их точность максимальна.

Тесно с определением набора показателей связано формирование выборки, поскольку, согласно эмпирическому правилу, необходимо, чтобы число параметров весов нейросети было больше объема выборки в 10 раз, при этом число весов сильно зависит от числа подаваемых в нейросеть признаков. Общей задачей в данном случае является максимизация выборки.

Также аналитику необходимо озаботиться нормализацией данных, поскольку многие функции активации обладают различной чувствительностью. Универсальным решением тут будет являться приведение подаваемых признаков в рамках интервала от 0 до 1.

Главная сложность использования нейронных сетей кроется в выборе способа конструировании и обучении сети. В силу того, что нейросетевое моделирование обладает относительно слабой теоретической базой по этому вопросу, их необходимо подбирать.