Проблемы применения теории зернистых сред в строительстве

Questions of approaches to the solution of granular mediums among foreign and native researchers are considered. First of all there was an objective about applicability of granular environments mechanics for earthwork and underground construction.

The review produced in article can be interest for subway builders. Also it can become a basis of more serious research for other types of construction.

We analysed a current state of research of mechanics of granular mediums and drew a conclusion: in matter the native science, despite priorities in researches of this direction, lags behind foreign experience and practically doesn't find applications. Considerable part of the scientists, who were occupied in the granular medium, went abroad and now they are demanded. Today, only enthusiasts are occupied in this matter in Russia. We want to revive native school of the granular medium.

Исследования по механике зернистой среды, проводимые в Санкт-Петербургском государственном политехническом университете, возникли из идеи применить в задачах геологии и геомеханики аппарат непрерывных (диффузионных) марковских процессов. В России с середины прошлого века марковскими процессами занимался А.А. Свешников [1]. Одним из первых вопросами механики зернистых сред в то же время начал заниматься академик Польской Академии наук Е. Литвинишин [2]. Основные достижения польской школы связаны с расчетом диффузионных перемещений зернистой среды. Диффузионные перемещения возникают при удалении внутри среды конечного макрообъема зернистого материала, после чего в возникающую полость начинают «проваливаться» зерна материала, среда приходит в движение и на ее поверхности возникает мульда сдвижения, не повторяющая форму первоначальной внутренней полости.

В зернистом материале всегда есть микропустоты (микрополости). Но если возникает полость конечных размеров, то мелкие зерна в нее ссыпаются по случайному закону и пустоты диффундируют к поверхности среды. Все это происходит даже в свободной (ненагруженной) среде.

Диффузионные перемещения являются характерной особенностью зернистой среды, их нет в упругой среде. Если из ненагруженного упругого материала извлечь конечный объем, то остальная часть среды останется без изменений и перемещаться не будет.

Зернистая среда в чем-то напоминает не твердое тело, а жидкость или газ, поэтому при расчетах желательно учитывать диффузионные перемещения. К такому заключению пришел российский ученый Р.А. Муллер [3] практически в то же время, что и Литвинишин. Появилась модель блуждающей частицы Литвинишина – Муллера. Но, к сожалению, Р.А. Муллер остановился в своих исследованиях, тогда как польская школа Литвинишина продолжила развиваться, и не только в Польше, но и в других странах.

Еще одно из направлений механики зернистых сред, также возникшее в середине прошлого века в СССР, было разработано И.И. Кандауровым [4,5]. Нужно признать, что хотя методически теория Литвинишина – Муллера для перемещений и теория Кандаурова для напряжений очень близки, но все-таки физически они относятся к разным задачам. Польские учёные и Муллер изучают диффузионные перемещения главным образом в свободной, ненагруженной среде. Кандауров изучает напряжения в нагруженной среде, т.е. компрессионные перемещения. Соответственно, для грунтовых условий теория Кандаурова более соответствует действительности. Но, теория Литвинишина реально работает во многих странах, а более совершенная отечественная теория применения практически не находит [6].

Компрессионные перемещения возникают только в нагруженной зернистой среде и аналогичны перемещениям упругой среды. Компрессионные перемещения Кандауров описывает с помощью закона Гука, хорошо известного для упругой среды. Эти перемещения имеют место в среде без макропустот и достигаются за счет уплотнения упаковки частиц, т.е. сжатия микропустот, а также за счет поджатия самих зерен среды. Это принципиально отличается от механизма диффузионных перемещений, основанного на диффузии пустот в зернистой среде.

В Санкт-Петербургском государственном политехническом университете группой ученых была предпринята попытка дополнить наиболее разработанную и совершенную теорию Кандаурова с учетом результатов Литвинишина и Муллера. При этом вся теория строилась на языке теории случайных марковских процессов в духе работ А.А. Свешникова [1, 7]. В свете возникающих здесь задач удалось выявить ряд перспективных направлений исследований.

Прежде всего, была предпринята попытка решения задач механики комбинированной среды. Комбинированной называют среду, скомпонованную из фрагментов с принципиально различными механическими свойствами (упругих, зернистых, абсолютно твердых и т.д.). Комбинированные среды хорошо известны в механике. Например, детально изучена упруго-пластическая среда. Все штамповые задачи соответствуют комбинации упругой и абсолютно твердой частичных сред. Новизна рассматриваемой модели заключалась в комбинации упругой и зернистых сред, имеющей слоистую структуру (см. рис. 1). Такая комбинированная зернисто-упругая среда употребительна в строительной механике и инженерной геологии, однако ранее детально не изучалась.

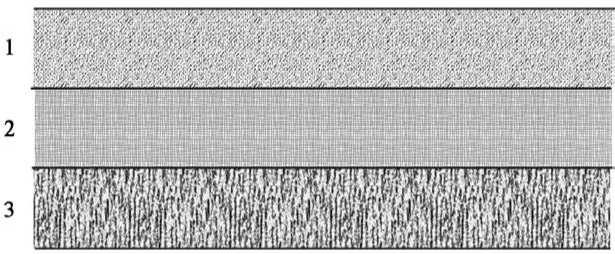
Рисунок 1 . Схема комбинированной зернисто – упругой среды

1 – зернистый слой; 2 – упругий слой; 3 – абсолютно твердое основание

Наиболее подробно методы расчета механических характеристик комбинированной зернистоупругой среды разработаны в монографии [8]. В монографии дается полные решения плоской задачи для слоистой упруго-зернистой среды с нижним упругим слоем, над которым располагаются несколько зернистых слоев. Приводится ряд новых результатов, касающихся расчета характеристик зернистой среды. Наиболее важны из них два:

• •    уточняется решение В. Бжонкала для задачи о касательной силе, приложенной к зернистому слою. Известно, что решение этой задачи впервые дал И.И. Кандауров [4, 5]. Однако с физической точки зрения оно содержит ряд недостатков. В. Бжонкала уточнил решение Кандаурова [9]. Тем не менее, в решении Бжонкала сохраняются физически противоречивые эффекты, например, зернистая среда, продолжает воспринимать растягивающие нагрузки. В монографии [8] эти дефекты устранены;

• •    в монографии [8] разработан метод расчета диффузионных перемещений для нагруженной среды, который отсутствовал в классических работах Е. Литвинишина и Р.А. Муллера. Это позволило рассчитать перемещения напряженной зернистой среды.

Модель, представленная в монографии [8], получила дальнейшее развитие и конкретизацию результатов в статье [10]. В ней детально изучается модель, когда над упругим слоем располагается только один зернистый слой. Особо выделен случай слабых напряжений, для которых решение [8] значительно упрощается (в квадратурах выражено через поверхностную нагрузку).

Наиболее законченный и доработанный вид решение [8] получило в статье [11]. В статье рассматривалось несколько зернистых слоев, а нижний упругий слой ослаблен круговым отверстием, моделирующим тоннель метрополитена (см. рис. 2).

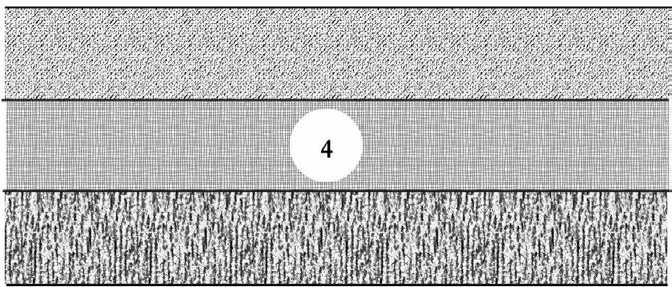
Рисунок 2 . Схема комбинированной зернисто–упругой среды с ослабленным круговым отверстием в упругом слое

1 – зернистый слой; 2 – упругий слой; 3 – абсолютно твердое основание; 4 – круглое отверстие в упругом слое

Далее были предприняты попытки решения контактных задач для зернистых сред. Впервые контактные задачи для зернистой среды начали рассматривать польские механики. Плоскую задачу о штампе рассмотрел С. Матысяк [12]. Он же решил с соавтором осесимметричную задачу [13]. При решении был допущен ряд неточностей, а само решение оказалось неполным. Работы содержат фактические ошибки, в них отсутствует расчет просадок штампа и искривления свободной поверхности в общем случае.

В Санкт-Петербургском государственном политехническом университете прежде всего было уточнено решение Матысяка осесимметричной задачи о штампе для среды И.И. Кандаурова. В классической постановке эта задача была решена [14]. С рядом усовершенствований данное решение было включено И.И. Кандауровым в сборник [15]. Более сложные модели штампов и штамп со срезом применительно к зернистой среде также изучались в СПбГПУ [16]. На основе этих моделей дано теоретическое объяснение, наблюдающимся на опыте при определенных условиях аномально большим просадкам штампов (так называемый «эффект проваливания свай»).

Следующий этап исследований, выполненных в СПбГПУ, предусматривал рассмотрение не одиночного штампа, а расчет свайного фундамента в предположении, что подстилающая среда является зернистой, а сваи моделируются с помощью штампов [17].

Далее исследования сосредоточились на решении динамических задач механики зернистых сред [18]. Рассматривалось движение зернистого полупространства, заполненного средой И.И. Кандаурова, после приложения к поверхности полупространства переменной нормальной нагрузки. Нагрузка считалась осесимметричной. Задача решалась методом интегральных преобразований. По времени применялось преобразование Лапласа, по радиусу – Ханкеля. Было установлено поведение среды после приложения постоянной сосредоточенной силы (задача Буссинеска для зернистой среды), а также постоянной нагрузки, равномерно распределенной в круге. Связь напряжений и деформаций описывалась законом Фойгта. Пусть σn обозначает напряжение в направлении n, а εn – деформацию сжатия. По Фойгту:

de

a = E — + 0—n), dt где E – модуль сжатия, θ – время релаксации деформаций. Когда θ→0, закон (1) переходит в хорошо известный закон Гука, применяемый в статических задачах.

В [18] детально рассмотрены два случая приложения нагрузки. Первый случай соответствует бесконечно большой скорости звука в среде:

γ =

E

ρ

где ρ обозначает плотность среды. Второй случай означает отсутствие внутреннего трения (θ=0), так что закон Фойгта (1) переходит в простейший закон Гука:

σn= Eεn.

Общий случай, когда скорость звука γ конечна и имеется внутреннее трение (θ≠0) разработан в [19], где для случая постоянной нагрузки найдены перемещения поверхности полупространства .

В СПбГПУ также была решена задача Лэмба для зернистого полупространства, исследовались поверхностные волны, вызванные сосредоточенной силой меняющейся по гармоническому закону. Были изучены частные случаи поверхностных волн: квазиупругая волна при отсутствии внутреннего трения (θ=0); неупругая волна при бесконечной скорости звука; неупругая волна при конечной скорости звука.

Результаты этих исследований докладывались на международных конференциях «Nondestructive testing and computer simulations in sciences and engineering» («Неразрушающий контроль и компьютерное моделирование в науке и технике»). (NDTCS). Все конференции проводились под эгидой SPIE (The society of photo-optical instrumentation engineers) и сборники трудов печатались в США. Участие группы ученых СПбГПУ в конференциях ограничивается 1998-2003 г.г. [19, 21]. Наиболее общая постановка динамических задач для зернистой среды была осуществлена в 2002 г. [22]. В ней вместо модели Фойгта, связывающей напряжения и деформации, предлагалось использовать модель стандартного линейного тела:

σn+ϑ

d σ _n dt

dr

= E — + 0- n ) . dt

Данная работа анализирует вертикальные перемещения в модели, для которой ранее были получены радиальные перемещения [19]. В выражении (4) все величины имеют тот же смысл, что и в (1), но добавлено время релаксации напряжений ϑ . Модель (4) широко используется физиками и математиками при рассмотрении динамических задач для твердых тел. Ее частным случаем ( 9 = 0 ) является модель Фойгта, кроме того при 0 = 0 имеем тело Максвелла [23, 24]:

σn+ϑ

d σ _n dt

=Eε

n

При одновременном обращении в нуль 0 , 9 приходим к модели Гука. Необходимость усложнения модели связи напряжений и деформаций по сравнению с простейшим законом Гука связана с тем, что поля напряжений и деформаций на практике не пропорциональны друг другу. Деформации отстают от напряжений. Аналогичная ситуация имеет место в зернистой среде. Напряжения устанавливаются достаточно быстро путем передачи усилий через контакты зерен друг с другом, а деформации и перемещения формируются значительно медленнее, так как требуется время на завершение диффузии пустот. Исходя из вышеизложенного, А.Н. Незлобин [25] предложил следующую классификацию зернистых сред: стандартная линейная среда Кандаурова (стандартное линейное тело Кандаурова, соответствующее закону (4)); среда Кандаурова-Фойгта (при включении в закон Кандаурова условия Фойгта (1)); среда Кандаурова-Максвелла (при включении в закон Кандаурова условия Максвелла (5)); среда Кандаурова-Гука (простейший случай, когда в закон Кандаурова включается закон Гука (3)).

А.Н. Незлобиным были изучены особенности деформирования всех этих сред под воздействием нормальной сосредоточенной нагрузки. Также им были рассмотрены вертикальные перемещения поверхности зернистого слоя , заполненного стандартной линейной средой Кандаурова при условии, что этот слой лежит на твердом основании [26]. Им же была решена задача для постоянной полосовой нагрузки, величина которой меняется по заданному закону [27]. О.И. Зайцем проведены вычисления просевшего объема зернистой среды для нормальной динамической нагрузки [28]. Н.Б. Явич предпринял попытку компьютерного решения для случая трехмерной структуры зернистой среды, но положительных результатов так и не достиг [29].

Исследованиями зернистой среды занимались в Военной академии тыла и транспорта [30, 31] и Военно-транспортном университете [32]. Но в силу военной специфики данных учреждений, получить более подробную информацию в открытой печати довольно затруднительно. Из наиболее доступных источников можно упомянуть только монографию А.В. Матвеева [33,34], который является личным учеником И.И. Кандаурова.

За рубежом, в основном, исследования зернистой среды проводятся исходя из предпосылок польской школы Литвинишина, более того, достижения И.И. Кандаурова игнорируются. В середине прошлого века в США в направлении школы И.И. Кандаурова работал профессор М.Е. Харр, но по признанию самого автора теории [5], результаты Харра, опубликованные в его монографии [35] не только не опровергают, но, напротив, подтверждают выводы И.И. Кадаурова, а конкретно в главах 7 и 8 [35].

В целом следует сделать вывод, что несмотря на приоритет в разработке многих проблем теории зернистых сред отечественными учеными, в настоящее время в России исследования возможности применения данной теории в строительстве почти не проводятся. В силу различных обстоятельств многие российские ученые, работавшие над этой теорией, оказались за границей. Желательно возрождение отечественной школы теории зернистых сред и ее применения в практике строительства.