Проблемы прочности: кинетическая концепция прочности, относительность и неопределённость

режимах нагружения и видах напряженного состояния могут быть объяснены и описаны на основе кинетических представлений. Многочисленные последующие исследования [3] убедительно показали справедливость зависимости, предложенной Н. С. Журковым, определяющей долговечность или время до разрушения при действии постоянных напряжений:

ПАУКО-ЖГРАДА ti = tо • exp(Uо -voi)/ RT,      (1)

где t 0 - период колебаний атомов, с (10^-13); U ₀ – энергия активации, ккал/моль; ν – структурно-чувствительный коэффициент, ккал^мм²/ моль^кг; о - действующее напряжение, кг/мм²; R - газовая постоянная, ккал/моль К; Т - температура, градусы Кельвина.

Влияние скорости нагружения на разрушающую нагрузку образцов было обнаруже-4    но практически сразу, как только наука о проч ности твердого тела получила экспериментальные подтверждения. Многие стандарты по определению механических характеристик материалов предполагают ограничение скорости нагружения для уменьшения фактических разбросов получаемых величин, отражающих стохастическую природу разрушения конкретного образца.

Формула Александрова - Журкова является следствием зависимости (1) и представляет собой критерий длительной прочности [2]:

ti

J [(exp( vo i IRT )) /

⁰                                (1а)

/( t ₀ • exp( U ₀I RT ))] dt = 1.

Если рассматривать вместо действующих напряжений о . отношение действующих напряжений к величине критического напряжения σk, характеризующего разрушение при действии постоянного напряжения в течение одной секунды, то формула Александрова – Журкова принимает вид ti

f[(exp( vo k / RT •о i / о _к ))/

0                                   (1b)

/( t ₀ • exp( U ₀/ RT ))] dt = 1.

Здесь физико-механическими константами материала являются: U ₀ - энергия активации (ккал/моль), численно равная энергии сублимации; νσ _k = В – константа разрушения, соответствующая времени пребывания под нагрузкой в течение одной секунды при температуре испытаний:

испытаний и фундаментальной константы – энергии активации.

Тогда зависимость (1) может быть представлена в виде ti = t0 • exp(U0 — B о i I о к )/ RT, (3) где о ./оk - параметр, соответствующий отношению действующего напряжения перенапряженной зоны к предельному, равному напряжению разрушения при длительности действия, равной одной секунде, при температуре испытаний (эксплуатации).

Зависимость (3) является фактически принципом относительности: долговечность определяется не абсолютным значением действующего напряжения, а отношением действующего напряжения к фактическому разрушающему напряжению при длительности действия напряжения в течение одной секунды, подтверждая философскую концепцию «все в мире ОТНОСИТЕЛЬНО».

Энергетический барьер, который необходимо преодолеть при разрушении в течение одной секунды, определится из соотношения ( U ₀ - B )/2,3 RT = 13 или ( U ₀ - B ) = 30 RT . (4)

На рис. 1 приведена диаграмма предельных состояний для трех условных материалов, имеющих величину энергий активации U ₀ [30,0; 45,0; 52,0] ккал/моль. Логарифм времени до разрушения при постоянных напряжениях lg t. для этих материалов соответствует прямым 1, 2, 3, проходящим через точку А 1 , имеющую координаты: lg t = 0 и о i /о _k = 1, равное отношению действующих напряжений к пределу кратковременной прочности при температуре испытаний. Кратковременную прочность при температуре 293 градуса Кельвина принимаем равной σ _b – условному пределу прочности, получаемому при испытаниях в течение от одной до десяти секунд. На диаграмме прямые 1 и 1 ' соответствуют U ₀ = 30,0 ккал/моль, прямые 2 и 2 ' соответствуют U ₀ = 45,0 ккал/моль, прямые 3 и 3 ' соответствуют U ₀ = 52,0 ккал/моль.

Точке А 2 соответствует величина энергетического барьера при температуре 20 ° C (293 K)

B = U ₀ - 30 RT = U ₀ - 0,06 T . (2)

Впервые константа В описана в [2]. Формула (2) является одним из следствий зависимости (1) и справедлива для любого материала, так как зависит только от температуры

30 RT = 30·0,002·293 = 17,58 ккал/моль.

Неопределенность при разрушении соответствует неопределенности величины фактического разрушающего напряжения σ _k при длительности действия в течение одной секунды для данного образца или конструкции.

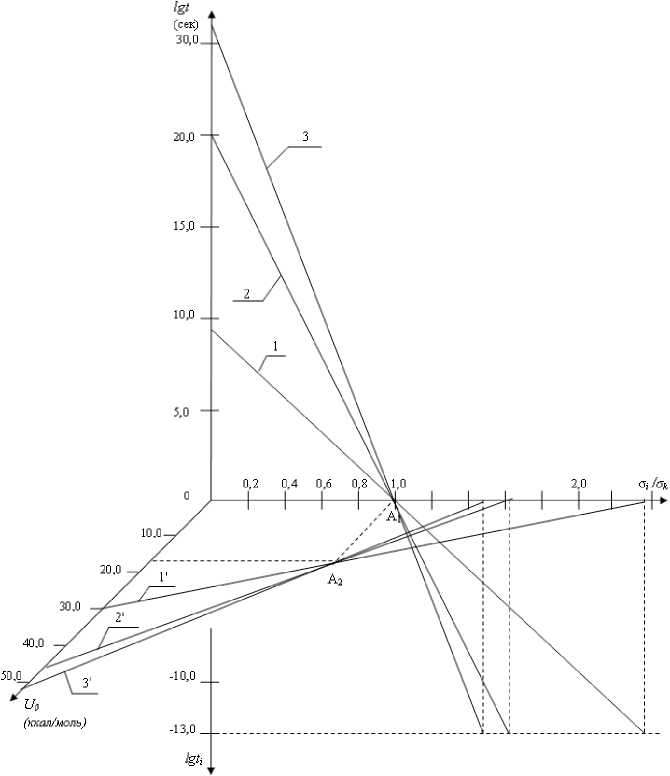
Рис. 1. Диаграмма предельных состояний

Большой разброс времени до разрушения, фиксируемый при длительных испытаниях с постоянным напряжением, может быть объяснен изменчивостью кратковременной прочности о _к , связанной с уровнем остаточных напряжений, степенью дефектности и неоднородности напряженно деформированного состояния в зоне развития магистральной трещины, предшествующей разрушению образца или элемента конструкции.

Следствием зависимости (1) и (3) являются формулы (4)–(8):

• •    критерий разрушения при длительном действии постоянного напряжения и постоянной температуры определяется по формуле

∫ ⁱdt [ t 0 ⋅ exp( U 0 -νσ i )/ RT ] =

= t / [ t о ■ exp( ^ о -vq i ) / RT ] =        (5)

= t i /[ t 0 ⋅ exp( U 0 - B σ i / σ k )/ RT ] = 1;

• •    критерий разрушения при постоянной скорости увеличения напряжения о₀ и постоянной температуре

ti

J [exp^{( vQ} _к / RT ■с о t / ^q k ) ■ dt ^]/

⁰    /[ t о ■ exp( ^ о / RT )] =

= [exp( B / RT ⋅σ ₀/ σ _k ⋅ t_j )]/ /[ B / RT ⋅σ ₀/ σ _k ⋅ exp( U ₀/ RT )] = 1;

• •    время до разрушения при постоянной скорости увеличения напряжений и постоянной температуре

t_j = [0,434( U ₀/ RT ) + lg t ₀ + lg σ ₀ - lg σ _k +

+ lg( νσ k / RT )]/[0,434( νσ k / RT ) ⋅ ( σ 0 / σ k )] =

= [0,434( U 0 / RT ) + lg t 0 + lg( σ 0 / σ k ) + ⁽⁷⁾ + lg( B / RT )]/[0,434( B / RT ) ⋅ ( σ 0 / σ k )];

• •    расходование ресурса несущей способности при постоянной температуре и постоянной скорости увеличения напряжений

lg r_j = 0,434[( νσ _k / RT ) σ ₀/ σ _k ⋅ t_j ] - lg t ₀ -

- lg( νσ k / RT ) - lg ( σ 0 / σ k ) - 0,434( U 0 / RT ) = ₈

= 0,434[( B / RT ) ⋅σ 0 / σ k ⋅ t j ] - lg t 0 -    ⁽⁾

- lg( B / RT ) - lg( σ 0 / σ k ) - 0,434( U 0 / RT ).

HAVKO____________

Ограда

Остаточный ресурс определяется зависимостью rост = 1 – rтек.                 (9)

Прогнозирование остаточного ресурса несущей способности как образца, так и конструкции при известной истории нагружения на основе кинетической концепции прочности является тем этапом, по Р Фейнману, когда наука дает инструмент для предсказания развития стохастического явления. В нашем случае ⁶ наука дает возможность прогнозирования вероятности разрушения при ожидаемых условиях эксплуатации.

На рис. 2 в относительных координатах t/t_j (где t_j – время до разрушения, t – текущее время нагружения) показано расходование ресурса несущей способности r при нагружении с постоянной скоростью увеличения напряжения σ₀ при температуре 293 градуса Кельвина для двух материалов, имеющих значения энергии активации U ₀ = 30,0 ккал/моль и U ₀ = 45,0 ккал/моль. Уменьшение скорости нагружения о 0 с 0,02 кг/мм²с до 0,0002 кг/мм²с привело к увеличению примерно на два порядка времени до разрушения, но в относительных координатах характер расходования ресурса практически не изменился.

Многие исследователи [5, 6], применявшие аппаратуру для фиксации эффекта акустической эмиссии, отмечают резкое изменение интенсивности и амплитуды акустических импульсов при нагрузке, соответствующей 90–95 % разрушающей величины.

Так, в работе [5] исследован процесс накопления повреждений при одноосном сжатии образца из композиционного материала, полученного смешиванием кварцевого порошка с диаметром частиц 10 мкм и эпоксидной смолы.

На рис. 3 приведены результаты расчета (кривая 3) остаточного ресурса образца из КМ, полученные по формуле (7) и кривые накопления повреждений из работы [5].

Практическое совпадение кривых 2 и 3, характеризующих темп накопления макротрещин и темп расходования ресурса несущей способности образца, свидетельствует о возможности прогнозирования разрушения на основании анализа интенсивности импульсов акустической эмиссии и знания закона расходования ресурса.

При экспериментальной проверке справедливости критериев разрушения необходи-

№ 2 (2) апрель-июнь 2012

мо для слабейших звеньев однонаправленного углепластика, какими являются матрица и поверхность контакта волокно-матрица, определить энергию активации матрицы и кратковременную прочность, соответствующую продолжительности действия разрушающего напряжения, равной одной секунде.

Первый метод определения U ₀ и σ _k связан с определением зависимости логарифма времени до разрушения lg t от постояннодействующих напряжений о . при постоянной температуре. Зависимость (4) показывает, что время до разрушения зависит от отношения действующего напряжения к напряжению, характеризующему кратковременную прочность.

Второй метод определения U ₀ и σ cвязан с определением t_j – времени до разрушения образца с разными скоростями нагружения σ₀. Алгоритм определения констант материала диктуется зависимостью (6) и предполагает наличие достаточного объема результатов испытаний.

Для конкретного образца (или элемента конструкции) кратковременная прочность является случайной величиной, зависящей от многих факторов. Для композиционных материалов к таким факторам относятся случайные свойства волокон, нарушение адгезии волокна и матрицы, неустойчивость технологического процесса, возможность выявления опасных дефектов, контроль расслоений и пористости и т. д. и т. п.

Расчетно-экспериментальный метод определения lg t j и о . основан на принципах планирования экстремальных экспериментов, широко применяемых в химической промышленности [7].

Анализируя зависимость (6), видим, что время до разрушения при известной скорости нагружения о₀ определяется константами материала U 0 и B , физическими константами R и 1 ₀, температурой испытаний. Поэтому стратегический план испытаний может быть построен при варьировании двух контролируемых параметров: скорости нагружения и температуры (табл. 1).

Рассмотрим ортогональный план второго порядка для k = 2 и n = 1.

Благодаря ортогональности матрицы планирования все коэффициенты регрессии определяются независимо друг от друга по формуле

Ь ) = 2 XY 2 X ,.■ (10)

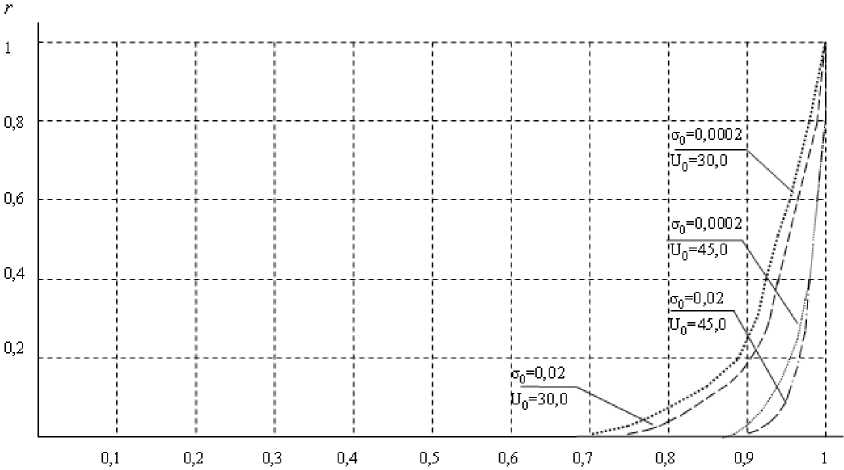
Рис. 2. Расходование ресурса несущей способности r при нагружении

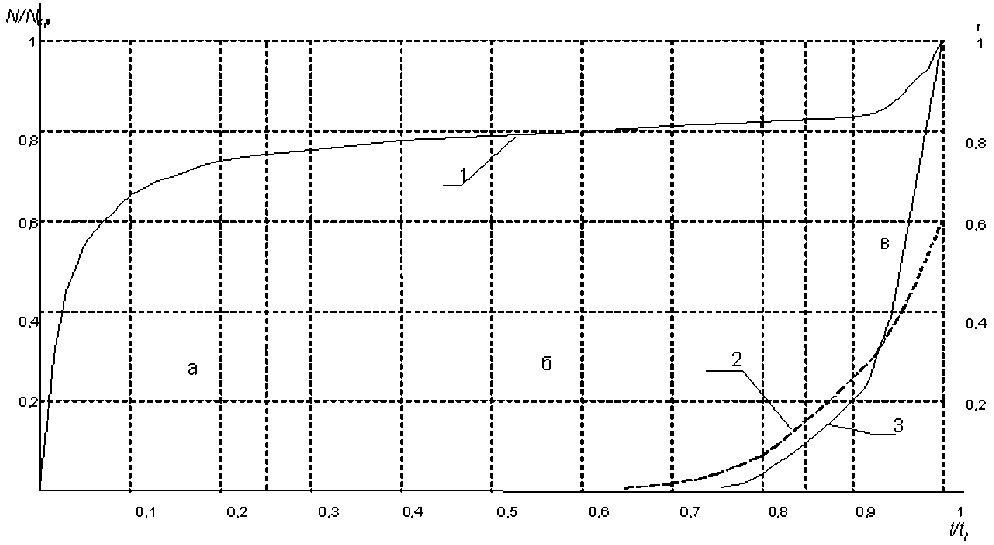
Рис. 3. Кривые накопления трещин при одноосном сжатии образца:

1 – общее число трещин; 2 – крупные трещины; а – начальный, б – стационарный, в – ускоренный участки

AVKO-

ЖГРАДА

Таблица 1

№ п/п	Х 0	Х 1	Х 2	ХХ 2	Х 1 *	Х , *
1	+1	+1	+1	+1	+1/3	+1/3
2	+1	+1	-1	-1	+1/3	+1/3
3	+1	-1	-1	+1	+1/3	+1/3
4	+1	-1	+1	-1	+1/3	+1/3
5	+1	+1	0	0	+1/3	-2/3
6	+1	-1	0	0	+1/3	-2/3
7	+1	0	+1	0	-2/3	+1/3
8	+1	0	-1	0	-2/3	+1/3
9	+1	0	0	0	-2/3	-2/3

X] = X j (2) - X j (2) = X (2) - £ X ji (2)/ N .

Таблица 2

№	X 1	X 2	U 0/ RT	B = U 0 - 0,06 T	0,434 U0 0 RT	B 0 RT	lg B / RT	(6) - 13	(9)+(2)	(10)+(8)	t , с
1	2	3	4	5	6	7	8	9	10	11	12
1	- 1	293							8,221	9,547	10,38
2	- 2	293	51,2	12,42	22,22	21,2	1,326	9,221	7,221	8,547	92,80
3	- 3	293							6,221	7,547	820,0
4	- 1	308							7,136	8,412	10,27
5	- 2	308	48,7	11,52	21,13	18,87	1,276	8,136	6,136	7,412	90,50
6	- 3	308							5,136	6,412	783,0
7	- 1	273							9,870	11,263	10,48
8	- 2	273	55,0	13,52	23,87	24,76	1,393	10,870	8,870	10,263	95,50
9	- 3	273							7,870	9,263	862,0

В результате расчетов по матрице с преобразованными столбцами для квадратичных эффектов получим уравнение вида y = b* + b X1 + b2 X 2 + b12 X1 X 2 + Ьц X* + b22 X *.

Чтобы перейти к обычной записи, b0 определим по формуле b0 = b0 - b11 X1(2) - b22X2(2).

Тогда получим y = b0 + b X1 + b2 X2 + b12 X1X2 +

^{+ b} 11 X 1(2) ^{+ b} 22 X 2(2) .

Предполагая неадекватность линейного уравнения регрессии, рассмотрим композиционный план второго порядка для двух уровней.

Обозначим через Х ₁ логарифм скорости нагружения. Принимаем диапазон варьирования этой скорости от 0,1 до 0,001 мм/с.

Соответственно, +Х . 1 = - 1 и - Х 1 = - 3.

Обозначим через Х , температуру испытаний. Принимаем диапазон варьирования от

273 до 303 градусов Кельвина (от 5 до 35 градусов Цельсия).

Соответственно, +Х 2 = 303 и - Х , = 273.

Центр плана Х 1 = 0 = - 2 и Х 2 = 0 = 293.

Проведем математический эксперимент, определяя время до разрушения по формуле (6) при U ₀ = 30,0 ккал/моль.

Результаты расчета времени до разрушения приведены в табл. 2.

Расчет коэффициентов регрессии приведен в табл. 3.

Коэффициенты уравнения регрессии равны:

b ₀= 17,7/9 =1,966; b 1 = -5,69/6 = - 0,95; b ₂ = - 0,076/6 = - 0,0126;

b ₁₂ = 0,030/4 = 0,00725; b 11 = b ₂₂ = 0.

Отсюда у = 1,966 - 0,95Х1 - 0,0126Х2 +

+ 0,00725 Х 1 Х , .            (11)

В качестве проверки корректности уравнения регрессии по формуле (11) определены значения у* . Погрешность вычислений не более 0,2 %.

Таблица 3

№ п/п	Х 0	Х 1	Х 2	Х 1 Х 2	X 2	X 2	y	yХ 1	УХ 2	УХ 1 Х 2	У X 2	у x 2	у	%
1	+1	+1	+1	+1	1/3	1/3	1,012	1,012	1,012	1,012	0,337	0,337	1,010	0,2
2	+1	+1	-1	-1	1/3	1/3	1,024	1,024	-1,024	-1,024	0,341	0,341	1,022	0,2
3	+1	-1	-1	+1	1/3	1/3	2,935	-2,935	-2,935	2,935	0,978	0,978	2,936	0,05
4	+1	-1	+1	-1	1/3	1/3	2,894	-2,894	2,894	-2,894	0,965	0,965	2,896	0,07
5	+1	+1	0	0	1/3	-2/3	1,016	1,016	0,0	0,0	0,339	-0,678	1,016	0,0
6	+1	-1	0	0	1/3	-2/3	2,914	-2,914	0,0	0,0	0,971	-1,942	2,916	0,1
7	+1	0	+1	0	-2/3	1/3	1,957	0,0	1,957	0,0	-1,304	0,652	1,953	0,2
8	+1	0	-1	0	-2/3	1/3	1,980	0,0	-1,980	0,0	-1,320	0,660	1,979	0,05
9	+1	0	0	0	-2/3	-2/3	1,968	0,0	0,0	0,0	-1,312	-1,312	1,966	0,1
	9						17,700	-5,690	-0,076	0,03	0,0	0,0

Для сравнения приведем результаты расчета времени до разрушения образцов из алюминиевых сплавов, для которых энергия активации U ₀ = 52 ±2 ккал/моль.

При Т = 293 градусов Кельвина для U 0 = = 50,0 ккал/моль имеем

В = 50,0 - 0,06 • 293 = 50,0 - 17,58 = = 32,42 ккал/моль.

Для U ₀ = 54,0 ккал/моль имеем В = 54,0 – – 17,58 = 36,42 ккал/моль.

Результаты расчета приведены на рис. 4.

Учитывая линейную зависимость логарифма времени до разрушения от величины разрушающего напряжения, достаточно иметь экспериментальные данные для двух максимально разнесенных по величине скоростей нагружения, исходя из возможностей испытательного комплекса INSTRON. Рекомендуемые скорости нагружения от 1 мм/мин до 0,0001 мм/мин, то есть скорости нагружения желательно иметь отличающимися на четыре порядка. При этом максимальная скорость нагружения не должна превышать значения, при котором начинают преобладать вязкоупругие свойства матрицы ЭХД МД.

Проведенный математический эксперимент продемонстрировал алгоритм расчетно-экспериментального получения значений констант материала, определяющих долговечность конструкции, возможность прогнозирования остаточного ресурса несущей способности и принципиальную возможность фиксации методом акустической эмиссии момента перехода к катастрофическому разрушению конструкции.

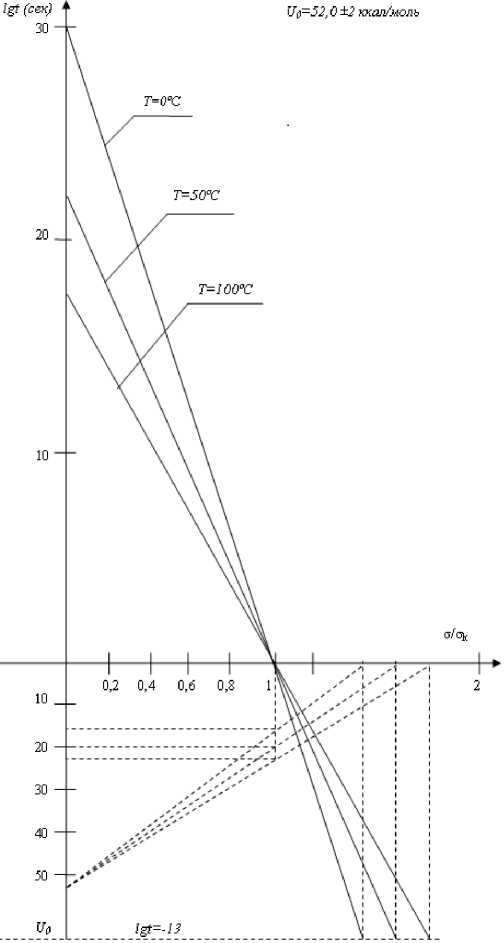
Рис. 4. Результаты расчета