Проблемы теории магнитосферных волн РС1. Обзор

Наш обзор посвящен так называемым ожерельям жемчужин (pearl necklace) — одному из самых загадочных волновых явлений в околоземном космическом пространстве. Жемчужины обнаружили Эйвин Саксдорф и Лейб Харанг в середине 30-х гг. прошлого века в обсерваториях Соданкюля и Тромсё (см. [Kangas et al., 1998; Raita, Kultima, 2007] ). В систематике ультранизкочастотных (УНЧ) электромагнитных волн естественного происхождения жемчужины относятся к виду Рс1 (диапазон частот 0.2–5 Гц) [Троицкая, 1964] . Общий взгляд на происхождение Рс1 состоит в том, что колебания зарождаются во внешнем радиационном поясе и распространяются к земной поверхности вдоль геомагнитных силовых линий [Troitskaya, Guglielmi, 1967] .

Рисунок дает представление о динамическом спектре колебаний. Событие, показанное на рисунке, наблюдалось перед местной полуночью. Сигнал записан с выхода индукционного магнитометра LEMI-30, установленного на высокоширотной комплексной магнитно-ионосферной станции Норильск (геомагнитные координаты Ф=65.3°, Λ=162.9°) при низком уровне геомагнитной активности ( K _p=1 + ). Серия колебаний состоит из квазипериодической последовательности структурных элементов. Их для

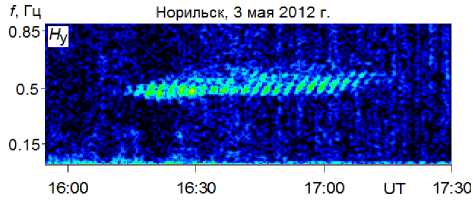
Динамический спектр УНЧ-волн вида Рс1

краткости иногда называют «райзингами» (rising), или сигналами растущего тона. В данном случае средний период повторения райзингов равен примерно 160 с. Длительность серии составляет около часа, ее несущая частота почти не меняется со временем, лишь немного повышаясь от 0.50 Гц в начале серии до 0.56 Гц к ее концу.

Удивительные свойства амплитудно-частотной модуляции колебаний, придающие неповторимое своеобразие ожерелью жемчужин, привлекают внимание космофизиков с середины 60-х гг. прошлого века [Yanagihara, 1963; Cornwall, 1965; Tepley, 1965; Troitskaya, Guglielmi, 1967]. В результате расчетов и целенаправленных наблюдений была сформулирована стандартная модель возбуждения и распространения волн Рс1, получившая широкую известность (см. например монографии [Гульельми, Тро- ицкая, 1973; Гульельми, 1979; Нишида, 1980; Gug-lielmi, Pokhotelov, 1996]). В первых двух разделах данной статьи мы кратко описываем основные положения стандартной модели.

С годами, однако, начали выявляться внутренние противоречия стандартной модели Рс1 и ее несоответствие опытным фактам. Наконец, к началу текущего тысячелетия остро встал вопрос о необходимости радикального пересмотра стандартной модели [Guglielmi et al., 2000] . В третьем разделе статьи мы описываем эту драматическую ситуацию. Она привлекла внимание многих исследователей. Проблемам, связанным с объяснением происхождения Рс1, был, например, посвящен специальный выпуск известного международного журнала [Kangas et al., 2007] , в котором подвергались сравнительному критическому анализу различные гипотезы о происхождении жемчужин [Demekhov, 2007] , сопоставлялись наземные и спутниковые наблюдения Рс1 [Mursula, 2007] , рассматривалось взаимодействие волн Рс1 с другими типами колебаний [Zolotukhina, Cao, 2007; Kurazhkovskaya et al., 2007] и высыпающимися заряженными частицами [Yahnin, Yahnina, 2007] . Интерес к загадкам жемчужин не утихает и по сей день. В последние годы особенно большое внимание уделяется спутниковым наблюдениям [Paulson et al., 2014; 2017] и их теоретической интерпретации [Klimushkin et al., 2010; Mikhailova, 2014; Некрасов, Фейгин, 2018] .

В четвертом разделе мы обсуждаем проблематику жемчужин в рамках феноменологической теории критических явлений. Наш общий вывод состоит в том, что необходима разработка новых идей вне рамок стандартной модели для понимания загадочных свойств возбуждения и распространения волн Рс1 в магнитосфере Земли.

1. ВОЛНОВОЙ ПАКЕТ

В основе стандартной модели Рс1 лежит фундаментальное представление о волновом пакете, распространяющемся в диспергирующей неравновесной среде. Волновой пакет ψ( x , t ) занимает в каждый данный момент времени ограниченный объем пространства. Под ψ мы понимаем какую-либо из ненулевых компонент переменного электромагнитного поля.

Чтобы не загромождать изложение, рассмотрим пакет, распространяющийся в направлении оси X в однородной безграничной и, на первых порах, консервативной среде. Для наглядности можно представить себе поперечные электромагнитные волны круговой поляризации, бегущие вдоль силовых линий однородного внешнего магнитного поля в холодной водородной плазме. Разложим ψ( x , t ) по нормальным плоским волнам и выберем начальную форму пакета в виде гауссиана с быстро осциллирующим заполнением:

V ( x , 0 ) = Ф 0 exp [ — ( x / x ₀ ) 2 + ik ₀ x J .

Здесь x — маршевая переменная; x ₀ — ширина пакета. Найдем соответствующую спектральную плотность

1 r

V _k (0) = I V ( x , 0 ) ^ex P ( — ikx ) dx = ^{2 n} -L

= V o exp

^-7 ^x 2^{( k — k} o ^{) 2}

где v₀ = Ф₀ x ₀ /2^п . (Мы воспользовались табличным значением интеграла [Градштейн, Рыжик, 1962] .) Смысл перехода к спектральному представлению состоит в том, что при t > 0 эволюция волн в k -пространстве тривиальна, а именно, каждая спектральная компонента просто осциллирует V _k ( t ) = V _k ( 0 ) exp [— i ^ю ( k ) t J , причем частота to( k ) определяется решением дисперсионного уравнения. (Относительно дисперсионного уравнения для плоских волн в холодной магнитоактивной плазме см. монографию [Гинзбург, 1967].)

Теперь раскладываем ω( k ) в ряд в окрестности k 0 , ограничиваясь первыми тремя членами, совершаем обратное преобразование Фурье и находим закон эволюции волнового пакета:

V ( x , t ) = V₀ exp ( ik ₀ x — i ®₀ t ) x

X

π

^ a + i в t

exp

—

^{( x -} v g t

4 ( a + i в t )

Здесь и₀ = to ( k ₀ ) , a = x 0 /4, в = ( dv_g / dk ) /2 при k = k 0 . Мы видим, что волновой пакет распространяется как целое с групповой скоростью v_g = d to / dk и испытывает дисперсию (расплывается). Фундаментальное понятие групповой скорости ввели независимо Стокс и Рэлей в 70-е гг. XIX в. Тогда же Умов интерпретировал v g как скорость переноса волновой энергии-импульса. Если v g зависит от частоты, то говорят, что среда является диспергирующей по отношению к данному виду волн. Заметим, что термин «групповая скорость» ввел Рэлей, а термин «дисперсия» восходит к Ньютону.

Нетрудно убедиться, что максимум амплитуды пакета, перемещаясь со скоростью v g , уменьшается со временем как (α²+β² t ²)^–1/4. Ширина пакета растет ( 2     2 2 1/2

a +в t ) . Полная энергия пакета сохраняется. При t> 0 спектральные компоненты перераспределяются внутри пакета таким образом, что при x=const мгновенная частота увеличивается с течением времени, если β<0, и уменьшается, если β>0.

Закон сохранения волновой энергии является следствием консервативности идеальной среды, выбранной нами в виде холодной магнитоактивной плазмы. В реальности волны поглощаются, их энергия переходит в тепло, но могут и усиливаться, если среда неравновесная, как это имеет место во внешнем радиационном поясе, где небольшая примесь энергичных ионов (преимущественно протонов) создает условия для возникновения ионноциклотронной неустойчивости [Cornwall, 1965]. Здесь, однако, есть нюанс, который не сразу вошел в структуру стандартной модели Рс1 [Troitskaya,

Guglielmi, 1967; Гульельми, 1979]. Дело обстоит следующим образом. В пионерской работе [Cornwall, 1965] начальное возмущение взято в виде монохроматической ионно-циклотронной волны, которая распространяется в однородной безграничной холодной плазме, содержащей примесь неравновесных энергичных ионов. Но модель монохроматической волны, заполняющей безграничное пространство, трудно адаптировать даже мысленно к условиям в радиационном поясе. Более того, мы покажем, что радиационный пояс сам по себе вообще не является генератором, а представляет собой усилитель ионно-циклотронных волн.

Выберем начальное возмущение в виде волнового пакета, как это было сделано нами выше, а отнюдь не в виде монохроматической волны. Заменим частоту ω в дисперсионном уравнении на комплексную величину ω+ i γ, мнимую часть которой принято называть инкрементом неустойчивости среды относительно волновых возмущений данного вида, если γ>0, или декрементом затухания волн, если γ<0. Вычисление γ в рамках реалистичных моделей среды является математически сложной и часто довольно

The problems of the Pc1 magnetospheric waves theory. A review громоздкой процедурой. Здесь нам достаточно будет допустить, что γ>0 в определенной полосе частот ω (или волновых чисел k ), и γ≤0 за пределами этой полосы.

Рассмотрим волновой пакет малой амплитуды в неравновесной среде. Допустим, что распределение γ в полосе нестабильности является унимодальным, как это и бывает во многих случаях (см. например, [Guglielmi, Pokhotelov, 1996] ). Разложим функции γ( k ) и ω( k ) в окрестности максимального значения инкремента:

Y = Y m ^— a ⁽ k ^— k m )\

® = ® m + v g ⁽ k ^— k m ^{) +} b ⁽ k ^— k m ^{) 2} •           ⁽³⁾

Здесь Y m =Y( k m ), to m =to( k m ), a = d ²Y/2 dk²      ,

1 k=km b = d to/2dk , ym>0, а>0.

¹ k = k m

Дальнейший расчет, вполне аналогичный указанному выше, приводит к следующему закону эволюции волнового пакета в неравновесной среде:

1/2

V ( x , t ) = V o

П

( a + ib ) t + x 2 /4

exp i i ( k m x -to m t ) + Y m t -

[ x - v g t ^{+ ix}0 ( ^km - ^k 0 ) ^/2 ] ²

4 ( a + ib ) t + x ²

—

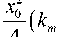
k 0 ) 2 ’ •

—

Амплитуда пакета увеличивается экспоненциально с течением времени благодаря тому, что свободная энергия неравновесной плазмы трансформируется в энергию волн.

Формула (4) позволяет ввести важное для теории Рс1 представление о существенном различии между абсолютной и конвективной неустойчивостями неравновесной среды [Лифшиц, Питаевский, 1979] . При абсолютной неустойчивости амплитуда увеличивается в любой точке пространства. Для этого, как следует из (4), должно выполняться неравенство

Y m >

2 v_ga

4 ( a ² + b ² )'

При обратном неравенстве неустойчивость является конвективной: амплитуда остается конечной в любой фиксированной точке пространства. Она экспоненциально увеличивается только лишь в системе отсчета, движущейся с групповой скоростью, например, в точке x = v g t . Заметим, что для ионноциклотронных волн в радиационном поясе с большим запасом выполняется условие конвективной неустойчивости. Это значит, что в радиационном поясе возможно усиление ионно-циклотронных волн, а отнюдь не их генерация.

• 2.    СТАНДАРТНАЯ МОДЕЛЬ

• 3.    ПРОБЛЕМЫ ИНТЕРПРЕТАЦИИ

  Красота, элегантность и глубина теории распространения волновых пакетов проявились в том, что из небольшого числа постулатов мы оказались способны логически вывести многообразие суждений об удивительных свойствах волн Рс1. Казалось бы, многие свойства жемчужин, если не все, удается понять и описать в рамках теории, по крайней мере, на качественном уровне. Но присмотримся к наклону структурных элементов на рисунке, он не изменяется с течением времени. Это грубо противоречит линейной теории расплывания волновых пакетов, поскольку теория предсказывает, что наклон элементов должен монотонно увеличиваться. Оригинальная гипотеза о происхождении аномальной дисперсии жемчужин была предложена в свое время в рамках квазилинейной теории неустойчивости плазмы [Фейгин, Якименко, 1969, 1970; Feygin, Kurchashov, 1975] . И все же проблему нельзя считать решенной, поскольку без альтернативных предположений мы не можем произвести экспериментальное тестирование гипотезы о квазилинейном механизме формирования дисперсии жемчужин.

Самовозбуждение ионно-циклотронных волн возможно в расширенной системе, которая включает в себя радиационный пояс и открытый резонатор. Резонатор образован геомагнитной силовой трубкой, опирающейся своими торцами на ионосферу в магнитосопряженных районах Северного и Южного полушарий. Волновой пакет, усиленный в радиаци- онном поясе, распространяется к Земле, достигает одного из торцов резонатора, частично отражается, поступает на вход усилителя, а далее процесс повторяется в противоположной полусфере. Если коэффициенты отражения от ионосферы достаточно велики, радиационный пояс переходит в режим генерации колебаний на частоте ионно-циклотронного резонанса tom =Qp ( cA / v||p ) , (6) где Ωp — гирочастота протонов на экваторе силовой трубки, cA — скорость Альфвена, v p — продольная компонента скорости энергичных протонов. Здесь для простоты принято условие cA ^ v|p. Таковы общие контуры стандартной модели возбуждения УНЧ-волн Рс1, изложенной более подробно в обзорах и монографиях [Troitskaya, Guglielmi, 1967; Гульельми, Троицкая, 1973; Guglielmi, Pokhotelov, 1996; Kangas et al., 1998].

В рамках стандартной модели интерпретация динамического спектра ожерелья жемчужин, представленного на рисунке, состоит в следующем. Фактически мы наблюдаем один и тот же пакет ионноциклотронных волн, который осциллирует вдоль геомагнитной силовой трубки, отражаясь от ионосферы в магнитосопряженных областях. Пакет периодически возвращается в радиационный пояс, усиливается, и процесс повторяется. Генерация колебаний происходит при условии, что приток энергии из радиационного пояса в волновое поле превышает потери, возникающие при отражении волн от ионосферы. Период повторения структурных элементов (см. рисунок) равен удвоенному времени пробега с групповой скоростью vg из одной сопряженной точки в другую. Несущая частота определяется резонансным условием (6). Рост частоты внутри отдельного структурного элемента объясняется тем, что ионно-циклотронные волны испытывают дисперсионное расплывание, причем параметр дисперсии отрицательный: β=dvg/2dk< 0 (см. формулу (2)).

Мы специально этого не оговаривали, но из контекста было ясно, что для анализа использовалась линейная теория распространения волн. Другими словами, амплитуда начального возмущения (1) предполагалась достаточно малой. В неустойчивой среде волновой пакет лишь короткое время эволюционирует по закону (4). Амплитуда пакета экспоненциально нарастает, и линейная теория становится неприменимой спустя время порядка 1/γ m после начала процесса. Подробный анализ нелинейной стадии эволюции не входит в нашу задачу. Мы ограничимся изложением одного сценария эволюции, интересного с физической точки зрения и, возможно, полезного для интерпретации наблюдений.

Качественно картина эволюции малых возмущений в усиливающей среде выглядит следующим образом. На линейной стадии начальные возмущения нарастают, причем их спектр быстро сужается и концентрируется в малой окрестности резонансной частоты ω _m =ω( k_m ). По мере роста амплитуды в действие вступают нелинейные процессы. Нелинейность называют диссипативной, если под действием волн модифицируется γ( k ), или консервативной, если модификацию испытывает ω( k ). Сосредоточим внимание на консервативной нелинейности и будем моделировать ее добавлением члена ηψ ² в правую часть второй из формул (3). Допустим, что выполняется критерий Лайтхилла η b <  0. Тогда возникнет модуляционная неустойчивость волнового поля. В результате произойдет уширение спектра, а это приведет к перекачке волновой энергии из области усиления (| k – k _res|<Δ k ) в область диссипации (| k – k _res|>Δ k ). Здесь Δ k — ширина полосы усиления. Таким образом, за счет перекачки по спектру амплитуда ψ стабилизируется.

Данный сценарий мы заимствовали из теории ветровых волн на воде [Андронов, Фабрикант, 1979] . Не исключено, что он может иметь место и в неравновесной плазме [Гульельми, 2008] . Обратим внимание на интересное обстоятельство. Принято считать, что модуляционная неустойчивость приводит к образованию солитонов. Оказывается, что в активной (усиливающей) диспергирующей нелинейной среде солитон не имеет свободных параметров. Его амплитуда, ширина и частота заполнения полностью определяются параметрами среды. Напомним, что солитон в пассивной среде имеет два свободных параметра, а именно, амплитуду и частоту заполнения. При этом ширина солитона определяется его амплитудой. В отличие от этого, в линейном волновом пакете, распространяющемся в пассивной среде, амплитуда, ширина и частота заполнения не зависят друг от друга, т. е. являются свободными параметрами (см. (2)).

Вторую проблему мы назовем проблемой дискретности. Суть ее в том, что в рамках линейной теории волн в диспергирующей неравновесной среде нет механизма стратификации динамического спектра, подобного показанному на рисунке. Как и в случае с аномальной дисперсией, мы вынуждены дополнить стандартную модель гипотезой о нелинейном механизме формирования квазипериодической последовательности структурных элементов. Иногда в этой связи говорят о структурном элементе серии жемчужин как о солитоне, но это не более чем общее направление мысли при поиске решения проблемы дискретности. Физического смысла в аналогии между жемчужиной и солитоном не просматривается.

Проблемы дискретности и дисперсии жемчужин можно назвать теоретическими в том смысле, что наблюдения свидетельствуют о четких стабильных свойствах колебаний, в то время как теория оказывается недостаточно изощренной, чтобы объяснить эти свойства. Кроме того, обе проблемы, судя по всему, относятся к теории нелинейных колебаний. В отличие от этого, третья проблема, которую мы здесь укажем, является, во-первых, экспериментальной, а во-вторых, может быть полностью сформулирована в рамках линейной теории распространения ионно-циклотронных волн. Мы назовем ее проблемой существования в магнитосфере ионноциклотронных резонаторов, или сокращенно — проблемой ICR (ion cyclotron resonator). Суть ее в том, что теория определенно указывает на существование ICR, но нам не удалось найти этому экспериментальных подтверждений, несмотря на наши усилия в этом направлении [Guglielmi et al., 2000, 2001; Гульельми, Потапов, 2012] .

Проблема ICR возникает в связи с наличием в магнитосфере небольшой примеси тяжелых ионов (например, ионов O+). Специфическая неоднородность геомагнитного поля в окрестности экваториальной плоскости играет ключевую роль в форми- ровании ICR. Однако мы условились не углубляться в сложную проблематику распространения волн в неоднородных средах. Поэтому ограничимся лишь кратким комментарием, а также указанными выше ссылками на оригинальные работы (см. также обзор [Гульельми, 2007]).

Основное отличие ICR от резонатора стандартной модели самовозбуждения жемчужин состоит в том, что точки отражения волн располагаются не в ионосфере, а высоко над Землей, в небольшой окрестности вершины той силовой линии геомагнитного поля, которая является осью резонатора. В этой связи возникает дополнительная проблема интерпретации, поскольку не ясно, как энергия волн, накопленных в ICR, переносится на Землю.

Любопытно, что период осцилляций волнового пакета между торцами ICR примерно равен периоду повторения структурных элементов серии жемчужин. Более того, линейный волновой пакет в ICR не расплывается, хотя он и распространяется в диспергирующей среде. Это частично решает первую из указанных нами проблем интерпретации. Остается не вполне ясным, почему мы обычно наблюдаем сигналы растущего, а, скажем, не падающего тона. Идея ICR, о существовании которого убедительно свидетельствует теория, позволила понять одно из фундаментальных свойств жемчужин — четкую антикорреляцию появления колебаний этого типа с 11-летним циклом солнечной активности, а именно, нам удалось связать эту закономерность с 11-летней солнечно-циклической вариацией плотности тяжелых ионов O⁺ в магнитосфере Земли [Guglielmi et al., 2001; Гульельми, 2007] . Вместе с тем теория ICR, будучи линейной, не дает никаких указаний относительно стратификации динамического спектра, отчетливо видимой на рисунке.

• 4.    ОБСУЖДЕНИЕ

Мы убедились, насколько сложной может оказаться интерпретация электромагнитных УНЧ-волн естественного происхождения. Многие космофизики, вооруженные весьма продвинутой теорией распространения волн в диспергирующих неравновесных средах, на протяжении более полувека интенсивного исследования не смогли разгадать загадку жемчужин. Наиболее трудной мы считаем проблему дискретности. Чтобы найти какой-то путь к решению проблемы, мы обратимся к теории критических явлений и начнем с феноменологической теории Ландау, адаптировав ее к нашему случаю.

Введем параметр порядка ε=|ψ|2, пропорциональный плотности волновой энергии в центре ICR, при необходимости усредненной по определенному интервалу времени. Уравнение эволюции имеет вид dε

= 2 Γε .                                        (7)

dt

Нелинейный инкремент Γ ( Λ , ε ) равен

Г( Λ , ε ) = γ ( Λ ) - αε ,                            (8)

где α — постоянная Ландау; Λ — управляющий параметр [Ландау, Лифшиц, 1988] (не следует путать параметр Ландау с параметром α в формуле (2).) Вблизи порога самовозбуждения линейный инкремент γ(Λ) пропорционален управляющему параметру:

γ ( Λ ) =β ( Λ-Λ _с). (9)

Здесь Λ _с — критическое значение Λ ; β — коэффициент пропорциональности. Теория ионноциклотронной неустойчивости радиационного пояса [Cornwall, 1965; Kangas et al., 1998] подсказывает выбор управляющего параметра Λ= N ( T _⊥ / T - 1).

Здесь N — концентрация энергичных протонов; T ,

T _± — продольная и поперечная температуры протонов. Таким образом, теория содержит три феноменологических параметра — α, β, Λ с .

В состоянии равновесия d ε / dt = 0. Равновесие может быть неупорядоченным, когда ε =0, или упорядоченным, когда ε≠ 0 при Γ ( ε , Λ ) = 0. Важное значение имеет знак α в выражении (8) для нелинейного инкремента. При α >0 говорят о динамической системе с мягким, а при α <0 — с жестким самовозбуждением колебаний. Квазилинейная теория взаимодействия волн и частиц в радиационном поясе предсказывает α >0. Судя по всему, при мягком режиме трудно ожидать формирования дискретности жемчужин. В самом деле, система с мягким самовозбуждением при Λ<Λ c характеризуется неупорядоченным состоянием, а при Λ>Λ с — упорядоченным. Во втором случае возбуждение колебаний происходит под влиянием сколь угодно малого возмущения и интервалы между райзингами в ожерелье жемчужин существовать не могут.

В этом отношении интереснее был бы режим жесткого самовозбуждения [Гульельми, Троицкая, 1973] . В отличие от динамической системы с мягким самовозбуждением, система с жестким самовозбуждением метастабильна в докритическом состоянии. Другими словами, она стабильна относительно бесконечно малых возмущений, но может перейти в автоколебательный режим под влиянием триггера, т. е. возмущения пусть небольшой, но конечной амплитуды. Однако конкретных механизмов жесткого режима в радиационном поясе пока что не найдено.

Интересным и перспективным нам представляется также развитие теории на базе идеи проточного резонатора. Она была предложена в работе [Гулье-льми, 1971]. Речь шла о резонаторе стандартной модели жемчужин, однако идея проточности безусловно применима и к ICR. Дело обстоит следующим образом. Боковые стенки открытого резонатора формируются системой каустик, т. е. они прозрачны для ионов радиационного пояса, дрейфующих с востока на запад в неоднородном геомагнитном поле. Таким образом, ICR «продувается» потоком горячих частиц, обладающих определенным запасом свободной энергии. За пределами резонатора свободная энергия не трансформируется в энергию волн, поскольку, как нами было отмечено ранее, неустойчивость распределения частиц радиационного пояса является конвективной. Однако внутри резонатора такая трансформация возможна и при вполне определенных условиях происходит самовозбуждение волн. Квазилинейное взаимодействие волн и частиц в ICR приводит к редукции свободной энергии, но поступление новых частиц восполняет потери. Оказывается, что текущее значение нелинейного инкремента Г в проточном резонаторе будет зависеть от предыстории эволюции волнового поля. Формально это обстоятельство выражается следующим образом:

t

Г( Λ , ε , t ) =γ ( Λ ) -η ∫ ε ( t ′ ) Φ ( t ′ - t ) dt ′ . (10) -∞

В работе [Гульельми, 1971] показано, что волновое поле разбивается на периодичную последовательность дискретных сигналов, если формфактор Ф=0 при t ′< t –τ и Ф=1 при t –τ≤ t ′≤ t . Здесь τ — время переноса энергичных частиц радиационного пояса поперек ICR. По ориентировочной оценке τ совпадает с периодом повторения жемчужин.

Идея проточного резонатора была подхвачена другими исследователями и получила некоторое развитие в ряде работ [Беспалов, Трахтенгерц, 1986; Тагиров и др., 1986; Трахтенгерц и др., 1986; Трахтен-герц, Демехов, 2002] на феноменологическом уровне. Работоспособной микроскопической теории построить не удалось, так что вопрос о механизме формирования дискретности жемчужин остается открытым. Ясно только, что дискретность, на которую обратил внимание еще Саксдорф в своей пионерской работе [Sucksdorff, 1936] , несовместима со стандартной теорией происхождения жемчужин.

В заключение данного раздела приведем спекулятивное рассуждение, которое, возможно, прольет некоторый свет на происхождение райзингов в серии жемчужин (см. рисунок). Допустим, что по той или иной причине Г=0, ε=0 при t = 0. Это может произойти в результате эволюции волнового поля в соответствии с уравнениями (7), (10). В момент t = 0 самовозбуждения колебаний не происходит. Однако при t > 0 в резонатор начинают поступать новые энергичные ионы радиационного пояса, дрейфующие с востока на запад и обладающие избытком свободной энергии (именно в этом и проявляется проточность ICR). По мере заполнения резонатора процесс самовозбуждения колебаний возобновляется. Вполне понятно, что более энергичные частицы заполняют ICR раньше, чем менее энергичные. Но это значит, что колебания относительно низкой частоты будут возбуждаться несколько раньше, чем колебания более высокой частоты в соответствии с резонансным условием (6). Другими словами, рост частоты в структурном элементе связан не с расплыванием волнового пакета, а с разбросом частиц радиационного пояса по скоростям. Нетрудно убедиться, что ω ∝ t , т. е. функция ω( t ) является выпуклой в пределах райзинга, что обычно и наблюдается на опыте.

ЗАКЛЮЧЕНИЕ

Мы произвели анализ открытых проблем физики магнитосферных волн Рс1 и убедились в том, что необходима разработка новых идей вне рамок стандартной модели для понимания удивительных свойств динамического спектра колебаний.

Вообще говоря, обогащение проблематики свидетельствует об успешном развитии той или иной области исследования. Однако указанные нами проблемы Рс1 остаются открытыми так долго, что это обстоятельство начинает вызывать беспокойство. Мы уверены, что коллективными усилиями в конце концов будет понят механизм формирования стабильных волновых структур, наблюдаемых нами на Земле и в космосе в виде ожерелья жемчужин. Свою надежду мы связываем, прежде всего, с идеей проточного ионно-циклотронного резонатора, располагающегося в экваториальной окрестности внешнего радиационного пояса.

Выражаем благодарность Б.В. Довбне, О.Д. Зотову, Б.И. Клайну и Ф.З. Фейгину за интерес к данной работе. Работа выполнена при поддержке РФФИ (проект № 19-05-00574), проекта Минобрнауки КП19-270, а также программ государственных заданий ИФЗ РАН (№ 0144-2014-00116) и ИСЗФ СО РАН (ФНИ II.16). Результаты частично получены с использованием ЦКП «Ангара»