Проблемы устойчивой обработки измерений в радиоинформационных системах

Рассмотрим основные проблемы, возникающие при создании методов математической обработки измерений в радиоинформационных системах, в частности при разработке методов оценивания измеряемых параметров и нахождения производных по данным измерений. Содержание и задачи математической обработки видны из обобщенной модели системы обработки измерений (рис. 1).

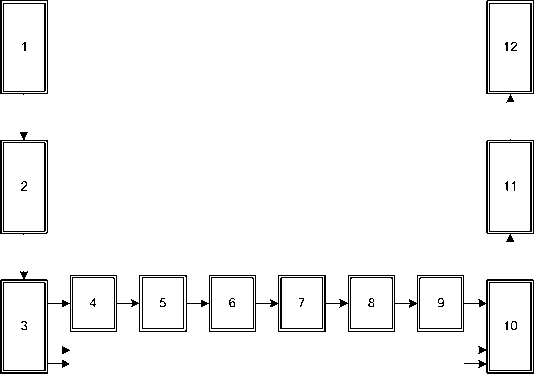
Рис. 1. Структура специального математического обеспечения

Модель можно представить в виде ряда унифицированных по структуре модулей, параметры которых определяются конкретными задачами измерений и структурой измерительной системы. Управление организацией модулей в приведенной модели не учитывается.

Тогда в самом общем виде обработка результатов измерений включает в себя следующие модули (рис. 1):

• 1    – ввод данных в систему обработки;

• 2    – отбраковку кодовых групп, не содержащих служебных сигналов;

• 3    – селекцию параметров из кодовых групп, выполняемую на основе признаков, характеризующих положение отдельных измерительных сигналов в группах;

• 4    – обнаружение полезного сигнала на фоне шума, в результате чего отбрасывается часть информации, где полезный сигнал отсутствует;

• 5    – масштабирование, т. е. определение физических значений измеряемого параметра;

• 6    – учет регулярных систематических ошибок;

• 7    – приведение измерений к единым моментам времени;

• 8    – прогнозирование значений измеряемых параметров вне участков измерений;

• 9    – оценку статистических характеристик распределения измеряемых параметров, авто- и взаимно корреляционных функций параметров, спектральных плотностей и т. п.;

• 10    – определение оценок измеряемых параметров и их производных;

• 11    – отбор существенных по каким-либо признакам значений измеряемых параметров;

• 12    – вывод результатов обработки измерений для отображения и дальнейшего использования при диагностике испытываемой системы, управления ходом эксперимента, а также для управления измерительно-вычислительным комплексом.

Количество цепочек из модулей 4–9 зависит от числа измеряемых параметров.

Далее мы сконцентрируем свое внимание на модуле 10 и рассмотрим его применительно к оцениванию параметров траектории движения летающих объектов и их производных. Точность и уровень автоматизации процесса получения искомых параметров существенно влияют на объем и продолжительность измерений, необходимых для получения требуемого результата.

Для повышения точности получения оценок измеряемых параметров целесообразно использовать при обработке все имеющиеся данные (что, как ни странно, иногда оспаривается). При этом достигается и непрерывность выдачи оценок вдоль всей траектории движения объекта.

Оптимизация оценки производится по полученной в результате эксперимента реализации случайного процесса. Методам оценивания параметров по данным измерений посвящена обширная литература. Однако часто предлагаемые методы при их использовании дают выводы, резко расходящиеся с истинным значением параметров. Погрешности оценок, которые теоретически должен гарантировать тот или иной метод оценивания, значительно расходятся с фактической точностью, полученной, например, путем сравнения результатов независимых определений параметров исследуемой системы. Как отмечено в [2], по-видимому, главной причиной такого расхождения между выводами, полученными классическими методами (наименьших квадратов, максимального правдоподобия, максимума апостериорной вероятности, фильтрацией по Винеру – Колмогорову и Калману), и практическими результатами является тот факт, что в этих методах пренебрегаются специфические особенности измерений, а также некоторые особенности поведения объектов измерения.

Рассмотрим эти о собенности и возможное их влияние на результат оценивания, а также проблемы, возникающие при создании методов, пригодных для обработки данных сложного эксперимента.

ВЕСТНИК РОСНОУ. Серия «Сложные системы…»

Средства измерений, например средства траекторных измерений и телеметрии, в процессе работы подвергаются интенсивным воздействиям, к которым можно отнести резкие, иногда даже аварийные изменения состояния оцениваемой системы, интенсивные возмущения среды, возникающие по условиям измерений, внешние и внутренние помехи. В результате реализуемые характеристики измерений, такие как плотности распределений вероятностей, корреляционные матрицы, математические ожидания погрешностей измерения, отличаются от априорно задаваемых при теоретическом построении метода оценивания. Непосредственное использование упомянутых классических методов ведет к возникновению дополнительных погрешностей при определении параметров, оценить которые с помощью классических методов не представляется возможным. Алгоритм оценивания обычно срабатывает, выдает «значение» оцениваемого параметра, но истинная ошибка неизвестна! Аналогично влияют на результат оценивания и погрешности в задании математической модели движения объекта, которые практически неизбежны вследствие сложного характера поведения объекта.

Таким образом, в общем случае вряд ли можно надеяться на то, что имеющаяся априорная информация настолько полна, что может быть в точности указана соответствующая плотность распределения или какие-либо необходимые менее информативные статистические характеристики. Но именно в надежде на это получены оптимальные алгоритмы, которые, несмотря на наилучшие теоретические характеристики, достигающие предельных возможностей, практически оказываются неработоспособными из-за нестабильности. Широко применяемая процедура отбраковки аномальных измерений ведет к потере информации и часто к отбраковке всех измерений. В этом случае естественно предполагать известной не точную плотность распределения помех, а некоторый класс принадлежности этой плотности распределения, стремясь при построении алгоритма оценивания к достижению стабильности, т. е. нечувствительности или слабой чувствительности оценок в условиях априорной неопределенности.

Дополнительные погрешности, возникающие при указанной неопределенности, особенно велики из-за часто имеющей место так называемой внутренней неустойчивости алгоритмов оценивания, которая обусловлена некорректностью, по Адамару [3], многих задач обработки измерений.

Поясним это на следующей стандартной линейной задаче оценивания. Состояние системы описывается реализацией случайного векторного процесса x (т), который задается матричным уравнением:

dx^^) = F (т) x (т) + g (т) u (Т), (1) d т x (0) = x0.

Измерения представляют собой векторный процесс

r (т) = C (т) x (т) + Э(т) (0 <т< T <да ). (2)

Здесь и (т) и Э(т) - выборочные функции гауссовых векторных шумов с нулевым средним; x ₀ - гауссова векторная случайная величина с нулевым средним и заданной дисперсионной матрицей. Известны корреляционные матрицы шумов M ^ u ( t ) u^T ( о ) J и M ^ v ( t ) v^T ( о ) J ( M - знак математического ожидания, T - транспонирования). Детерминированные матрицы соответствующих размерностей F (т), g (т), C (т) считаются заданными. Требуется построить линейный фильтр, который порождает условное математическое ожидание:

x ( t ) = M [ x ( t )| r (т), 0 <т< t ] .

Известно, что при линейности (1), (2) и гауссовости и ( т ) и Э ( т ) x(t ) - оптимальная в среднеквадратичном смысле оценка случайного процесса x ( t ) по наблюдениям { r ( т ), 0 <т< t } . Импульсная переходная функция (ИПФ) оптимального линейного фильтра h ( t, т ) удовлетворяет известному уравнению Винера - Хопфа:

M [ x ( t ) r T ( а ) ] = J h ( t , т ) M [ r ( t ) r T ( a ) ] d т .                      (3)

Конкретный вид уравнения (3) зависит от того, что представляет собой корреляционная функция шумов измерений v ( т ) . Этим в основном определяется и конкретный алгоритм решения задачи оценивания.

Широко известный фильтр Калмана - Бьюси требует существенного использования предположения о том, что шум v ( т ) - белый, т. е. M ^ v ( t ) v^T ( а ) ^ = R ( t ) 8 ( t -а ) , где 8 ( t - а ) - дельта-функция Дирака, R ( t ) - положительно определенная матрица. Вместе с тем реальные характеристики погрешностей элементов ИВК, используемых для обеспечения испытаний, обычно не удовлетворяют этим предположениям. Средства измерений существенно разнородны и поэтому значительно различаются по уровню интенсивности шума и по виду корреляционных связей.

Это дает основание считать достаточно типичными и общими следующие виды корреляционных связей:

• 1)    шум измерений v ( т ) является выходом известной линейной системы с детерминированными коэффициентами, возбуждаемой белым шумом;

• 2)    шум измерений v ( т ) - белый, матрица R ( t ) - вырожденная (в частности, может быть R ( t ) ^ 0 );

• 3)    шум измерений v ( т ) - «чисто цветной», т. е. элементы корреляционной матрицы являются функциями, интегрируемыми с квадратом по Лебегу.

Уравнение (3) при этих видах корреляционных связях является уравнением Фредгольма I рода, задача же его решения, вообще говоря, поставлена некорректно [3]. Поясним это несколько подробнее.

Приведем понятие корректно поставленной задачи в операторной форме [3]. Пусть H и Ф - нормированные пространства, A - оператор с областью определения D A с H и областью значений Q A = A ( D A с Ф ) . Пусть функция f еФ . Рассматривается задача отыскания функции h е D A , удовлетворяющей уравнению

Ah = f .                                    (4)

Обозначим R(f, A ) оператор, обратный к A . Задача (4) называется корректно поставленной по Адамару, если выполняются следующие условия:

• 1)    оператор R(f, A ) определен для всех f еФ , Q A = Ф ;

• 2)    элемент h = R(f, A ) заданием f еФ определен однозначно;

• 3)    при малых вариациях правой части f (в метрике пространства Ф) решение h = R(f, A ) задачи (4) меняется также мало (в метрике пространства H).

Если хотя бы одно из перечисленных условий нарушается, то задача называется некорректно поставленной. Рассмотрим пример, показывающий некорректность задачи (3).

Пусть h 1 (t, т ) является решением уравнения (3). Подставляя функцию

2 лго

2 лю А ^т t

h2 (t, т) = h1( t, т) + N-----cos в соотношение (3), получаем при K(т, а) = M ^r(т)rT (а)] и f (t, а) = M [x(t)rT (а)] t

J h ₂ ( t , т ) K ( т , а ) d т = / ( t , а ),

ВЕСТНИК РОСНОУ. Серия «Сложные системы…»

где

t

J cos 0

Таким образом, h ₂ является решением уравнения (3) с правой частью f ˆ .

Найдем расстояние между f и f в метрике пространства L 2 [ 0, t ] :

2 лго f ( t , о ) = f ( t , о ) + N—

т I K ( т , о ) d т .

If - f

L ₂

2 tt

, T2 । 2лю Iff | 2лю I 7 = N |-----I      cos |-----т IK(т,о)dт x / о L о     \        /

d о.

Последний интеграл является коэффициентом Фурье в разложении функции ^d

—K ( t, о ) в ряд по синусам d т

[ cos | ^^._т | к ( т , о ) d т = о 2 t J

t d d . 2 2 лго I                   t t . 2 2 лго I d

=         sin I----т| K(т, о)dт = -      sin I----т|—K(t, о)dт

2лго о dt   2 t J              2лю J0 2 t J dт и стремится к нулю. Подставляя его в (5), получаем

II f - f

L ₂

t ²

2 г г . ( 2 лго I d               ,

= N sin ---- т —K ( т , о ) d о .

J J I t   J d т

t

Таким образом, это выражение можно сделать сколь угодно малым при соответствующем выборе ω.

Найдем расстояние между h ₁ и h ₂ в пространстве решений.

Далее будет показано, что решение существует и лежит в пространстве с негативной нормой W ₀ ^{- 1} ; далее введена соответствующая техника этих пространств:

II ^ 1      ^h 2 11 ^ ₀ ^{- 1}

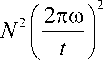
По определению нормы в W ₀ ^{- 1} имеем:

2 2лю cos ----т

2 t

= sup w0-1     y *0

2 2лю cos ----т

I t

Wo’

I" cosf ^^т^ y ( т ) d т

о 2 t 2

.

y w ^{- 1}

Интегрируем по частям выражение в числителе:

2 2лю I           t r d .2 2лю I           t г • 2 2лм । dy , cos |       т|y (т)dт =            sin | т ly(t)dт =        sin I I dт.

2 t J         2лю 0 dт 2 t J         2лю о 2 t J dт

Подставляя последнее выражение в (8) и учитывая, что

y_{W 0} 1 , получаем

dy d т L2

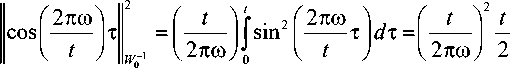
Используя это соотношение в (7), получаем

IIhi -h2It= N.

Выбирая в этом соотношении N большим, а затем в выражении (6) ю - достаточно большим, находим, что расстояние между правыми частями сколь угодно мало, а расстояние между решениями равно N ² 1 /2 , т. е. решение неустойчиво.

Таким образом, нарушенным оказывается третье условие корректности. Кроме того, некоторые задачи оценивания могут оказаться неоднозначными.

Очевидно, что понятие корректности задачи зависит от функциональных пространств, в которых ее рассматривают, и метрик, которые в них определяют. Может оказаться, что задача корректна в одной паре пространств и некорректна в другой. Разумеется, каждая конкретная задача должна рассматриваться в естественных для нее пространствах. Исследование условий корректности или некорректности решения соответствующей задачи само по себе является достаточно сложной проблемой.

Заметим, что задача построения упомянутого фильтра Калмана - Бьюси является теоретически корректной, поскольку она эквивалентна решению интегрального уравнения второго рода - корректной задаче, за счет невырожденного белого шума в наблюдениях.

В литературе известны попытки получить решение задачи фильтрации с небелым шумом в наблюдениях без учета некорректности задачи. Но в этих случаях авторам либо удавалось получить алгоритмы решения при некоторых ограничениях на исходные данные (задача оказывалась корректно поставленной), либо алгоритмы решения оставались некорректными (см. обзор в [1]), или предполагалось дифференцирование реализаций компонент наблюдаемого процесса или их линейных комбинаций. Иногда формального решения задачи можно достигнуть за счет ее дискретизации. В [2] приведено такое решение для вырожденного случая.

Рассмотрим особенности этого решения на примере.

Уравнение состояния системы второго порядка имеет вид:

" x 1 ( d k + 1 ) 1 = ГФ_П ( d k _{+ 1},d k ) Ф_п( d k _{+ 1},d k ) _ X 2 ( d k jJ Ф 2i ( d k ₊ i ,d k ) Ф 22 ( d k ₊ i ,d k )

^X 1^{( d}k ) x 2^{( d}k )

Г„( d k ) 0

0        U i ( d k )

Г ₂₂( d k ) JL u ₂( d k )

X i (0) x ₂(0)

X 1 ⁰

x 2

где

Ф ( d k _{+ 1},d k ) = dF ( d k ) + T + 0( d ² );

Г ( d k ) = dg ( d k ) + 0( d ² );

d - шаг дискретизации; k = 0, 1, 2, ..., n ; 0( d ²) - бесконечно малая. Наблюдения проводятся по закону

r ⁽ d k ) =

I

C i ( d k )

0      х Л d k ) + 0

c ₂( d k ) J[ % ₂( d k ) J [ v ( d k )

Шум объекта u - с нулевым средним и корреляционной матрицей:

M [ u ( d k ) u T ( d ) J = Q ( d k ) 8 kj , 8 kj

1, k = j

0, k * j

Шум измерений v - с нулевым средним и корреляционной матрицей:

M [ v ( d k ) v^T ( d ) J = R 1 ( d k ) 8 k =

0    0

0 R ( d k )

⁸ kj .

ВЕСТНИК РОСНОУ. Серия «Сложные системы…»

Предполагается, что случайные величины u ( d k ) и v ( d k ) - некоррелированы между собой и с вектором начальных условий: ^ х ° , x 0 I T | .

Необходимо получить оценку вектора состояний по заданной последовательности { r ( d k ) } k _{= 1} такую, чтобы минимизировать среднеквадратичную ошибку.

По [4] запишем алгоритм дискретной фильтрации. Уравнение фильтра

Х(d k ) = Ф ( d k ,d k J x ( d k J + K ( d k ) [ r ( d k ) - C ( d k ) Ф ( d k ,d k J, x ( d k _ ! > ] , x (0) = 0.

Коэффициент усиления фильтра имеет вид:

K ( d k ) = P ( d k J C T ( d k ) [ C ( d k ) P ( d k J C T ( d k ) + R ( d k ) ] ^{- 1} .

Уравнение дисперсии ошибки:

P ( dk\d k J = Ф ( d k ,d k - ) P ( d k - 1 ) Ф T ( d k ,d k J + Г ( d k J Q ( d k - 1 ) Г T ( d k J,

P(dk J = [1 -K(dk JC(dk-1)]P(dk-1 dk-2), где P(dk I dk-1) - априорная дисперсия ошибки, P(dk I dk-1) = M [(x(dk) - x(dk-1))2 ], x(dk I dk-1) - оценка вектора x(dk) по {r(dk-1)}k, т. е. результат одношагового предсказания; P (dk) = M [(x (dk) - x( dk ))2 ] - апостериорная ошибка оценивания.

Устойчивость дискретной фильтрации в рассматриваемом случае (корреляционная матрица погрешностей измерений вырождена) достигается путем применения в алгоритме фильтра одношагового предсказания - использования априорной дисперсии ошибки, которая определяет область, где находится так называемое главное решение задачи. Переход от априорной дисперсии к апостериорной в выражении для коэффициента усиления некорректен, так как матрица C ( d k ) P ( d k ) C T ( d k ) = 0.

Алгоритм регулярен только при условии несингулярности матрицы:

*( d k ) = C ( d k ) P ( d k \ d k J C^T ( d k ) + R ( d k ).

Устойчивость алгоритма зависит от степени обусловленности матрицы Т( d k ), причем здесь наибольшее влияние имеет матрица P ( d k I d k _{- 1}) . Если матрица P ( d k I d k _{- 1}) вырождается при некотором к , то алгоритм расходится. Обусловленность матрицы Т( d_k ) зависит от точности оценки. Чем точнее оценка, тем матрица Т( d_k ) хуже обусловлена, и малые погрешности в задании исходных данных модели вызовут большие ошибки при вычислении Т( d_k ) . Кроме этих ограничений, рассматриваемый подход требует и определенных ограничений на вид корреляционной матрицы начальных условий (вектора начального состояния).

В некоторых случаях необходимо получать значения оценок на коротких временных участках с малым интервалом дискретности поступления данных. При этом алгоритм оценивания целесообразно иметь непрерывным. Но, как показано выше, переход от дискретного алгоритма фильтрации к непрерывному в общем случае невозможен.

Возвращаясь к условиям 1) - 3), отметим, что различные частные методы, обладая несомненными достоинствами, не позволяют избавиться от некорректности задачи в общей ситуации. Кроме того, оказывается неясным, в каком смысле понимать решение задачи фильтрации при этих условиях. Действительно, решения рассматриваемых задач сводятся к решению интегральных уравнений первого рода, которые могут не иметь «обычных», интегрируемых с квадратом решений.

Вместе с тем можно достичь существенных результатов, используя метод регуляции А.Н. Тихонова и технику негативных и позитивных гильбертовых пространств.

Решение исходной задачи линейной фильтрации, когда в наблюдениях содержится любой из указанных выше типов шумов, сводится в конечном счете к отысканию импульсной переходной функции как решения соответствующего регуляризованного уравнения второго рода или к соответствующему модифицированному фильтру Калмана – Бьюси, зависящему от параметра регуляризации. При численной реализации этих подходов появляется целый ряд специфических проблем. В частности, если возникает необходимость решения регуляризованного интегрального уравнения, то целесообразно иметь некоторый приближенно-аналитический метод решения, использование которого ведет к значительному сокращению объема вычислений по сравнению с непосредственным численным решением интегрального уравнения. Использование приближенно-аналитического метода решения задачи фильтрации позволяет по-новому решить проблему управления измерениями, или, иными словами, найти оптимальную стратегию измерений.

Значительное влияние на эффективность работы регуляризованных алгоритмов оценивания в смысле близости результатов к истинному состоянию системы оказывает способ выбора параметра регуляризации. Проблеме выбора параметра регуляризации по априорным данным посвящены многие работы, например [3]. Однако с целью повышения точности оценок в каждом отдельном эксперименте необходимо иметь метод выбора параметра регуляризации, который согласовывал бы его значения с характеристиками измерений, реализовавшимися в этом конкретном эксперименте. Причем в случае получения рекуррентного метода, обеспечивающего подстройку параметра регуляризации в естественном масштабе времени, начальное значение параметра выбирается известными методами по априорным данным. Проблема построения статистического метода выбора параметра регуляризации по реализации измерений является достаточно важной. По существу, такой метод делает соответствующую регуляризованную систему оценивания адаптивной.

Кроме того, наличие к настоящему времени большого объема вычислительно-экспериментальных данных по применению регуляризованных алгоритмов оценивания позволяет указать для соответствующей задачи с достаточно высокой степенью достоверности некоторые интервалы значений параметра регуляризации (как случайной величины), что в свою очередь позволяет на основании знания реализации наблюдаемого процесса построить апостериорное распределение параметра регуляризации. Данный подход открывает возможность получения устойчивых алгоритмов оценивания с распараллеливанием вычислительного процесса и отысканием оценок с предельно возможной точностью, которую обеспечивает данный класс ЭВМ.

К проблеме построения устойчивых адаптивных оценок тесно примыкает задача дифференцирования функции, известной приближенно. И хотя различным аспектам этой задачи посвящены многие работы, открытой остается довольно важная проблема построения устойчивых алгоритмов восстановления производной от функций, имеющих скачки в виде разрывов первого рода, и обобщенных функций.