Процедура формирования программы номинального управления гелиоцентрическим движением космического аппарата с солнечным парусом с использованием законов локально-оптимального управления
Автор: Р.М. Хабибуллин
Журнал: Космические аппараты и технологии.
Рубрика: Ракетно-космическая техника
Статья в выпуске: 1, 2020 года.
Бесплатный доступ
Работа посвящена некомпланарному межпланетному перелету Земля-Венера космического аппарата, оснащенного солнечным парусом. Целью гелиоцентрического движения является попадание космического аппарата с неидеально отражающим солнечным парусом в сферу Хилла Венеры с нулевым гиперболическим избытком скорости. В работе используется неидеально отражающая модель солнечного паруса, величина и направление ускорения от которого рассчитывается с учетом зеркального и диффузного отражений, поглощения и пропускания фотонов поверхностью солнечного паруса. Одной из главных задач в области навигации и управления движением космического аппарата является поиск простой энергоэффективной схемы управления для выполнения того или иного маневра. Именно такими схемами управления и являются законы локально-оптимального управления, различные комбинации которых позволяют выполнить необходимые маневры при межпланетном перелете. Описана процедура формирования программы управления для некомпланарного межпланетного перелета типа Земля-Венера космического аппарата с неидеально отражающим солнечным парусом. В качестве результатов получены траектория перелета, изменение фазовых координат во времени, графики изменения управляющих углов и сформированная программа номинального управления. Полученные результаты удовлетворяют всем граничным условиям, описанным в постановке задачи.
Неидеально отражающий солнечный парус, закон локально-оптимального управления, программа номинального управления, некомпланарный межпланетный перелет
Короткий адрес: https://sciup.org/14115934
IDR: 14115934 | УДК: 629.78 | DOI: 10.26732/j.st.2020.1.01
Текст научной статьи Процедура формирования программы номинального управления гелиоцентрическим движением космического аппарата с солнечным парусом с использованием законов локально-оптимального управления
Солнечный парус (СП) – это приспособление, использующее давление солнечного света на отражающую поверхность для приведения в движение космического аппарата (КА) [1]. Значительное преимущество использования СП состоит в том, что он способен заменить двигательную установку на борту малого КА. Отсутствие рабочего тела позволяет существенно уменьшить массу всего КА и продлить срок его активного существования. За прошлые десять лет большой опыт использования СП был получен космическими агентствами США, Европы и Японии [2–7].
Одной из главных задач в области навигации и управления движением КА является по-
иск простой энергоэффективной схемы управления для выполнения того или иного маневра. Подобные способы управления не обязательно должны быть близки к оптимальным. Основным требованием, выдвигаемым к подобным способам управления, является простота анализа и реализации. Именно такими схемами управления и являются законы локально-оптимального управления (ЗЛОУ), различные комбинации которых позволяют выполнить необходимые маневры при межпланетном перелете [8]. ЗЛОУ предназначены для наискорейшего изменения и сохранения одного из оскулирующих элементов орбиты, таких как: большая полуось A , фокальный параметр p , эксцентриситет e , радиус афелия r α, радиус перигелия r π, аргумент перигелия w , истинная аномалия ϑ, наклонение i , долгота восходящего узла Ω.
Целью работы является разработка процедуры формирования программы номинального

KI/IE АППАРАТЫ Ш
Том 4
управления КА с неидеально отражающим СП на базе ЗЛОУ для совершения некомпланарного межпланетного перелета на примере перелета Земля-Венера.
-
1. Постановка задачи
Рассматривается межпланетный некомпланарный перелет КА с неидеально отражающим СП с гелиоцентрической орбиты Земли к Венере. КА выведен из сферы действия Земли с помощью разгонного блока. Цель перелета – попадание в сферу Хилла планеты – области пространства, в которой могут двигаться тела, оставаясь спутником планеты, при этом интеграл энергии КА h < 0.
Введем вектор фазовых координат X , описывающий движение центра масс (ЦМ) и движение вокруг ЦМ в комбинированной системе координат:
X=(r, u, Vr, Vu, q i, e p, e n, e,, ® p, ® n, ®,) T, где r – гелиоцентрическое расстояние КА с СП; u – аргумент широты; Vr, Vu – радиальная и трансверсальная скорости; Ω – долгота восходящего узла орбиты; i – наклонение орбиты; θp, θn, θs – углы поворота СП, описывающие ориентацию КА с СП; ωp, ωn, ωs – угловые скорости.
Для описания управления ориентацией СП вводится вектор номинального управления U :
U = {5 p (t), 5, (t )}T, где δp(t), δs(t) – функции номинального управления, определяющие вращение СП относительно ЦМ, которые могут принимать следующие значения:
8 p ( t ) = { + 1,0, - 1) 1
•
-
8 , ( t ) = { + 1,0, - 1}
Фиксированный вектор проектных параметров prm КА с СП описывается следующим образом:
prm ={m, 5, p, pr, pd, a, t, hтэy f, где m – масса КА с СП; S – площадь СП; ρ – коэффициент отражения поверхности СП; ρr – коэффициент зеркального отражения поверхности СП; ρd – коэффициент диффузного отражения поверхности СП; α – коэффициент поглощения фотонов поверхностью СП; τ – коэффициент пропускания; hТЭУ – ширина тонкопленочных элементов управления.
Параметры вектора фазовых координат X и вектора управления U должны удовлетворять следующим ограничениям:
18 p ( t )| + |5 , ( t )| < 1
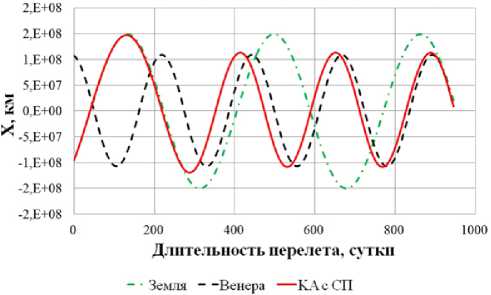
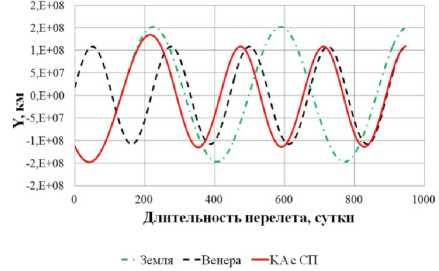
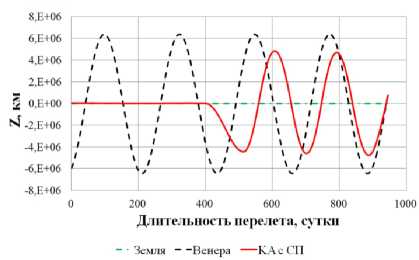
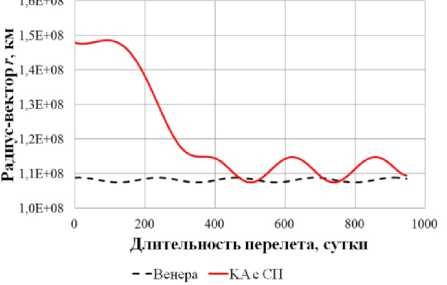
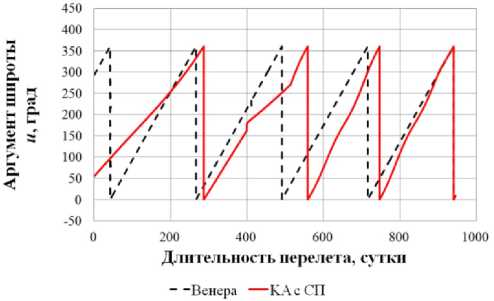
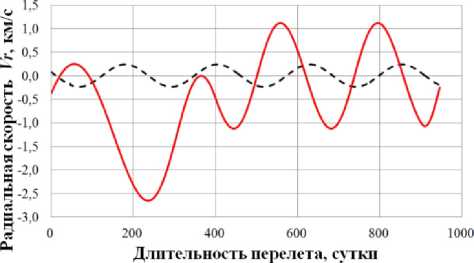
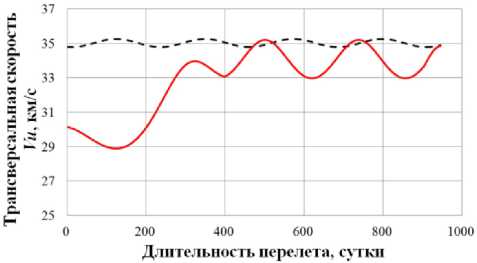
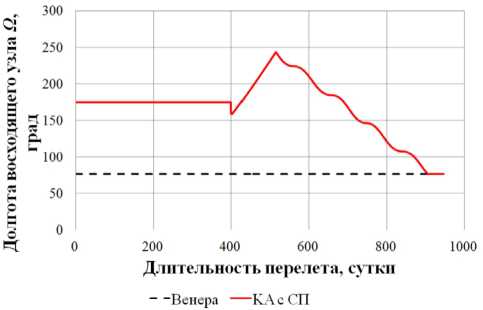
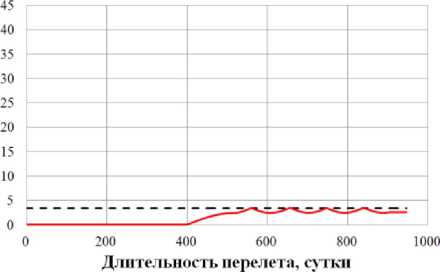
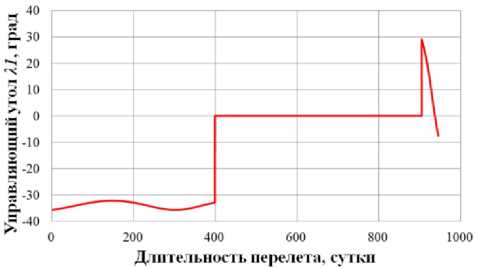
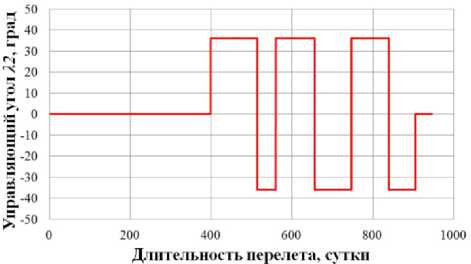
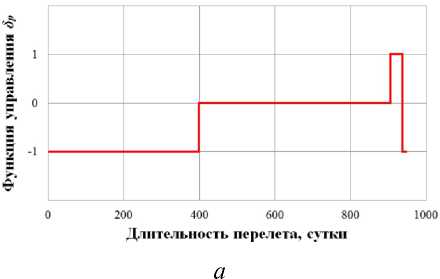
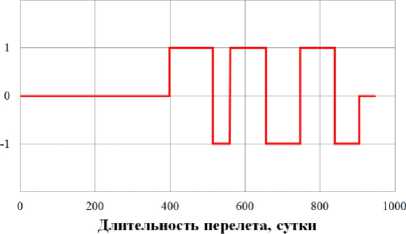
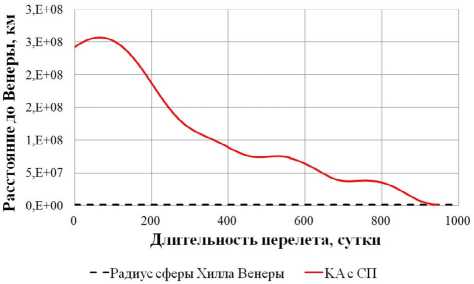
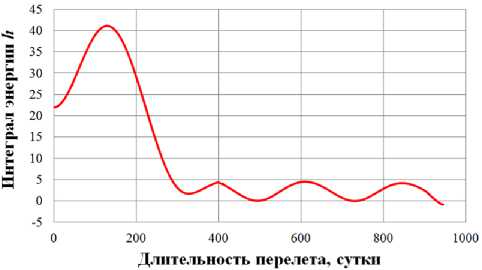
0)л <|to| Граничные условия гелиоцентрического перелета записываются следующим образом: X(10) = X 0, X(tk) = Xk. В качестве основного критерия оптимальности выбрано минимальное время перелета tk → min при условии: Dist(Г, u, Q, i) < Rxuo„a 1 h (Dist, Vr, V) < 0 где Dist – текущее расстояние между КА с СП и целью; RХилла – радиус сферы Хилла планеты. Интеграл энергии h определяется следующим образом [9]: h=∆V2- 2µцель . Dist Здесь ∆V – разность полных скоростей КА и планеты, к которой совершается перелет; μцель – гравитационный параметр планеты. Вектор функции управления U, удовлетворяющий ограничениям (1) и граничным условиям (2) и доставляющий минимум критерию оптимальности при фиксированном векторе проектных параметров prm, описывается следующим образом: Uopt(t) = arg min tk (U| Prm G P,X(t0) = Xo,X(tk) = Xk) - Задача сложная, поэтому предлагается процедура решения, состоящая из трех частей: 1. Получение номинальной программы управления движением ЦМ КА. 2. Определение максимальных необходимых угловых скоростей для обеспечения полученной программы номинального управления, расчет параметров органов управления. 3. Моделирование совместного движения ЦМ и вокруг ЦМ для демонстрации реализуемости полученной программы управления. 4. Данная статья посвящена первому пункту задачи – получение номинальной программы управления движением ЦМ КА. 2. Законы локально-оптимального управления В работе [8] автором получены ЗЛОУ для КА с двигателем малой тяги. В работе [7] автор сформировал ЗЛОУ для КА с СП. В рамках данной работы ЗЛОУ предназначены для определения управляющих углов λ1 и λ2. Угол λ1 – это угол между направлением падения фотонов на поверхность СП (совпадает с направлением радиус-вектора r) и проекцией нормали СП на плоскость орбиты движения КА. Угол λ2 – это угол между нормалью СП и ее проекцией на плоскость орбиты движения КА. Более подробно математическая модель движения КА с неидеально отражающим СП описана в [10]. Управляющие углы λ1 и λ2, обеспечивающие наискорейшее изменение оскулирующего элемента K, могут быть вычислены из следующего отношения: dK 2 1,2 opt = argmax ^1,2. . Г п n! dt -кI При λ1 = ±π/2 выполняется закон сохранности оскулирующего элемента во времени. Для обеспечения максимальной скорости изменения одного из элементов гелиоцентрической орбиты закон управления должен быть записан в следующем виде [11]: 1 f2 (з) (к (з) - V9IfN?+8if(3)f) X K = — arcsin------—;--------------—------- 2 3([fl (»)]! +[ f2(S)]2) , где f1 и f2 – компоненты, определяющие максимальную скорость изменения соответствующих орбитальных элементов. Для монотонного изменения наклонения орбиты i необходимо изменять направление тяги на противоположное в точках, где аргумент широты u = ±π/2. Для монотонного изменения долготы восходящего узла Ω необходимо осуществлять изменение управления в точках на линии узлов, в которых аргумент широты u = 0 и u = π. При λ2 = ±π/2 выполняется закон сохранности оскулирующего элемента во времени. Для обеспечения максимальной скорости изменения одного из оскулиру-ющего элемента, отвечающего за изменение положения орбиты в пространстве, закон управления должен быть записан в следующем виде: XK = ^ arcsin ^p- Sign [ f (u, X2], где Sign[f(u,λ2)] – функция определения знака в зависимости от значения аргумента широты u и управляющего угла λ2. В качестве примера рассмотрим ЗЛОУ для наискорейшего увеличения одного из элементов: - наискорейшее увеличение большой полуоси A: X. = -arcsin (-1 + ecos9) (ecos9- ^9[ecos9]2 + 8[-1 + ecos9]2) 3([ e cos 9]2 +[-1 + e cos 9]2) наискорейшее увеличение фокального параметра p: p 1 22 Xp =- arcsin 12 3; - наискорейшее увеличение эксцентриситета e: (ecos29 + 2cos9 + e) sin 9 — 9[sin 9]2+ 8 X. = — arcsin ecos 9 + 2cos9 + e 1 + ecos9 \ 3(1 + ecos9) [sin 9]2 I + e cos29 + 2 cos 9 + e 1 + ecos9 2; - наискорейшее увеличение радиуса афелия rα: X1a (2(1 + cos 9) - e sin29) sin9 - 9[sin 9]2+ 8 — arcsin 2(1 + cos 9)- esin2912 1+ecos9 к 3(1 + ecos 9) [sin 9]2+ к 2(1 + cos9)-esin29 1 + ecos9 7.; (оСМИЧЕскиЕ АППАРАТЫ И Том 4 - наискорейшее увеличение радиуса перигелия rπ: (2(1 - cos9) + esin2d) - sin 9- 9[sin 9]2+ 8 X? = - arcsin 2(1 - cos9) + esin2912 1 + ecos9 л \ 3(1 + ecos9) [sin 9]2+ I 2(1 - cos9) + esin29 1 + ecos9 ; - наискорейшее увеличение аргумента перигелия w: sin 9(2 + e cos 9) - cos9-д 9[cos9]2+ 8 , sin 9(2 + ecos9) 2 w Xi - arcsin 1 + ecos9 \ 3(1 + ecos 9) [cos 9]2+ I sin 9(2 + e cos 9) 2 1 + ecos9 ; - наискорейшее увеличение наклонения i: 1 22 [cosusinX2]; X2 = — arcsin —^— Sign - наискорейшее увеличение долготы восходящего узла Ω: 1 22 X, = arcsin 22 Sign [sin u sin X2 ]. 3. Формирование программы номинального управления Для определения параметров орбиты и положения Венеры используется база данных Лаборатории реактивного движения НАСА (Jet Propulsion Laboratory NASA) [12]. Дата старта Xra(to) = (1,479'108км; 54,953 град; -0,371 км/с; 30,122 км/с; 174,806 град; 0,004 град) миссии – 16 ноября 2027 года, дата завершения миссии – 19 июня 2030 года. Начальное положение КА с СП на дату старта и конечное положение Венеры опишем размерными фазовыми координатами в виде X = (r; u; Vr; VM; Q; i) T : T ХВен(ta^Ч) = (1,086-108км; 8,886 град; -0,199 км/с; 34,894 км/с; 76,595 град; 3,394 град)T. Данные о перелете представлены в табл. 1. описаны в табл. 2. Одна итерация моделирования Алгоритм и длительность использования ЗЛОУ соответствует 1 часу движения. Таблица 1 Данные о перелете КА с неидеально отражающим СП с орбиты Земли к Венере № п/п Наименование Значение 1 Цель Венера 2 Радиус сферы Хилла RХилла, км 1 008 000 3 Дата старта D0 16.11.2027 4 Дата завершения перелета Dк 19.06.2030 5 Масса КА с СП m, кг 39,8 6 Площадь СП S, м2 500 7 Длительность перелета, сут. 946 8 Расстояние до цели Dist, км 849 396 Таблица 2 Алгоритм использования ЗЛОУ № п/п Закон управления Дата начала этапа Дата завершения этапа Начальное значение Конечное значение Длительность, сут. 1 Уменьшение A 16.11.2027 18.12.2028 1,000 а.е. 0,724 а.е. 399 2 Увеличение i 18.12.2028 28.05.2029 0,004 град 3,385 град 161 3 Уменьшение Ω 28.05.2029 09.05.2030 224,017 град 76,651 град 345 4 Уменьшение e 09.05.2030 18.06.2030 0,052 0,007 41 Траектория гелиоцентрического движения КА с СП в плоскости XOY и изменение координат во времени представлены на рис. 1–2. Рис. 1. Гелиоцентрическая траектория перелета КА к Венере (▲ — КА; • — Венера; ☼ — Солнце; – · – орбита Земли; – – орбита Венеры; –– траектория КА) На рис. 3 представлены графики изменения фазовых координат во времени. Программа управления включает в себя изменение управляющих углов и функции управления. Использование ЗЛОУ подразумевает изменение положения КА и ориентации СП в пространстве. На рис. 4 приведен график зависимости управляющих углов λ1 и λ2 во времени. Графики функций управления δp и δs представлены на рис. 5. На рис. 6 представлено изменение расстояния между КА и Венерой на протяжении всего перелета. Как видно из рис. 6 на дату завершения миссии расстояние между КА и Венерой стало меньше радиуса Хилла Венеры. На рис. 7 представлен график изменения интеграла энергии, значение которого на дату завершения перелета меньше нуля. Для реализации гелиоцентрического перелета КА с неидеально отражающим СП с орбиты Земли к Венере на расстояние 849 396 км потребовалось 946 суток. Определена безразмерная величина интеграла энергии h = -8,7∙10-4. Найденные расстояние между КА с СП и Венерой Dist и ин- теграл энергии h удовлетворяют условию (3), следовательно, по окончании гелиоцентрического 9 участка КА остается в окрестности Венеры. а б Рис. 2. Зависимость координат положения КА во времени: а - координата X; б - координата Y; в - координата Z (– · – Земля; – – Марс; –– КА) Том 4 б --Венера --КА с СП —Венера —КА с СП в г ■Венера —КА с СП д е Рис. 3. Изменение фазовых координат КА во времени: а - радиус-вектор r; б - аргумент широты u; в - радиальная скорость Vr; г - трансверсальная скорость Vu; д - долгота восходящего узла Ω; е - наклонение i (– – Венера, –– КА) а б Рис. 4. Зависимости управляющих углов во времени: а - угол λ1; б - угол λ2 Рис. 5. Зависимости функции управления во времени: а - функция управления δp; б - функция управления δs Рис. 6. Изменение расстояния между КА и Венерой (– – радиус сферы Хилла Венеры, –– КА) Рис. 7. Изменение интеграла энергии h Заключение Рассмотрен некомпланарный межпланетный перелет Земля-Венера КА с неидеально отражающим СП, целью которого являлось попадание КА в сферу Хилла Венеры с нулевым гиперболическим избытком скорости. Для формирования номинального управления движением КА использовались законы локально-оптимального управления. Для реализации гелиоцентрического перелета Земля-Венера КА массой 39,8 кг с неидеально отражающим СП площадью 500 м2 потребовалось 946 суток. В качестве результатов получены траектория перелета, изменение фазовых координат во времени, графики изменения управляющих углов и программа номинального управления. Полученные результаты удовлетворяют всем граничным условиям, описанным в постановке задачи. Результаты моделирования подтверждают адекватность применения процедуры формирования программы номинального управления КА с неидеально отражающим СП.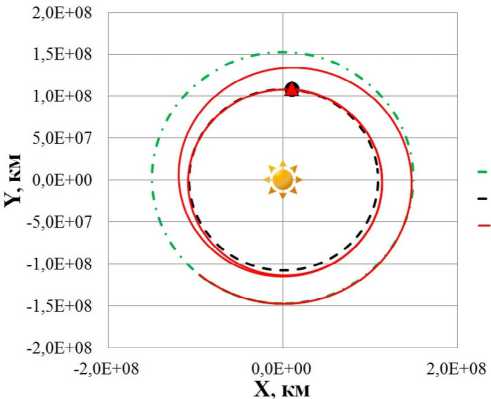

Список литературы Процедура формирования программы номинального управления гелиоцентрическим движением космического аппарата с солнечным парусом с использованием законов локально-оптимального управления
- Поляхова Е. Н. Космический полет с солнечным парусом. М. : Книжный дом «ЛИБРОКОМ», 2011. 320 с.
- Macdonald M. Advances in Solar Sailing // Materials of the Third International Symposium on Solar Sailing Glasgow. 2013. 977 p.
- Johnson L., Whorton M., Heaton A., Pinson R., Laue G., Adams C. NanoSail-D: A solar sail demonstration mission // Acta Astronautica, 2011, vol. 68, pp. 571-575.
- Mori O., Sawada H., Funase R., Morimoto M., Endo T., Yamamoto T., Tsyda Y., Kawakatsu Y., Kawaguchi J. First Solar Power Sail Demonstration by IKAROS // Transactions of the Japan Society for Aeronautical and Space Sciences, Aerospace Technology, 2010, vol. 8, issue 27, pp. 25-31.
- Biddy C., Svitek T. LightSail-1 Solar Sail Design and Qualification // Materials of the 41st Aerospace Mechanisms Symposium, 2012, pp. 451-463.
- Heiligers J., Diedrich B., Derbes B., McInnes C. R. Sunjammer: Preliminary End-to-End Mission Design // Materials of AIAA/AAS Astrodynamics Specialist Conference, 2014.
- McInnes C. R. Solar sailing: technology, dynamics and mission applications. Springer Science & Business Media, 2013, 296 p.
- Лебедев В. Н. Расчет движения космического аппарата с малой тягой. М. : ВЦ АН СССР, 1968. 108 с.
- Мирер С. А. Механика космического полета. Орбитальное движение. М. : Резолит, 2007. 270 с.
- Хабибуллин Р. М. Программа управления для некомпланарного гелиоцентрического перелета к Венере космического аппарата с неидеально отражающим солнечным парусом // Вестник Самарского университета. Аэрокосмическая техника, технологии и машиностроение. 2019. Т. 18. № 4. С. 117-128.
- Ишков С. А., Старинова О. Л. Оптимизация и моделирование движения космического аппарата с солнечным парусом // Известия РАН. 2005. Вып. 7. № 1 (13). С. 99-106.
- JPL Solar System Dynamics [Электронный ресурс]. URL: https://ssd.jpl.nasa.gov (дата обращения: 27.09.2018).


