Процедура корректировки фазовой функции фокусатора по результатам вычислительного эксперимента

ПРОЦЕДУРА КОРРЕКТИРОВКИ ФАЗОВОЙ ФУНКЦИИ ФОКУСАТОРА ПО РЕЗУЛЬТАТАМ ВЫЧИСЛИТЕЛЬНОГО ЭКСПЕРИМЕНТА

Для создания элементов плоской оптики (ЭПО) [1] характерно то, что расчет фазовых характеристик производится геометрическими методами, в то время как исследование структуры световых полей, создаваемых ЭПО, может быть осуществлено лишь в рамках дифракционной модели. Для оценки качества работы ЭПО на этапе проектирования актуальным является вопрос исследования и компенсации дифракционных эффектов, связанных с технологией расчета и изготовления ЭПО.

В данной работе рассматривается задача коррекции фазовой функции фокусатора с повышенной глубиной фокуса с целью компенсировать возникающие вследствие дискретизации радиальной фазовой функции дифракционные эффекты.

Фокусатор с повышенной глубиной фокуса

На радиально-симметричную оптическую систему (рис. 1) с функцией фазового пропускания Т(г) падает световой пучок с комплексной амплитудой Е(г). В дальнейшем считается, что оптическая система состоит из классической непрерывной собирающей линзы с фокусным расстоянием f0 и расположенного вплотную к линзе плоского оптического элемента - фокуса-тора, концентрирующего излучение в тонкий продольный цилиндр на оптической оси. Функция фазового пропускания фокусатора <р(г) определяется системой дифференциальных уравнений [2]:

Л ।                      г

Ь' (г) +       •• ф'(г) --- ----

R             V r2+(f0+z(г)И

w(z)z'(г) = Ву(г) • 2пг                                                 (1)

z (0) = 0, z (а) = к

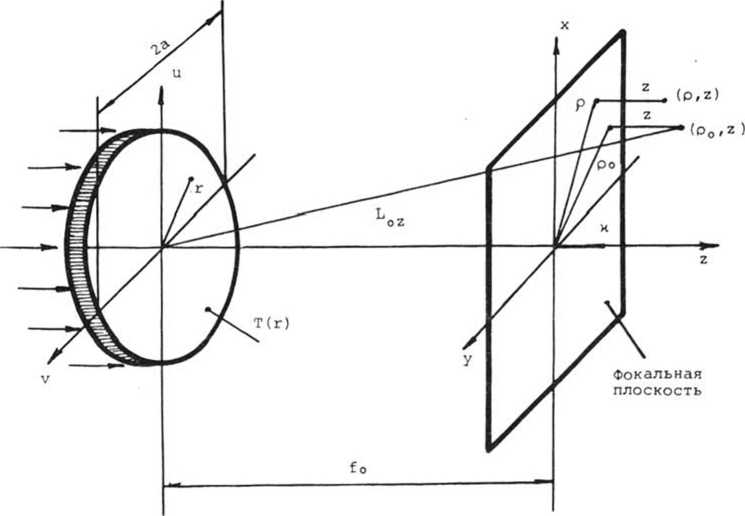
Рис. 1. Оптическая схема работы ЭПО

Здесь (г, а) - полярные координаты в плоскости фокусатора и с началом в его центре; w(z) - линейная плотность мощности на отрезке фокусировки [0, к]; Во(г) и Ь(г) - соответственно амплитуда и фаза падающего на фокусатор светового пучка; X - длина волны света; а - радиус фокусатора. При f₀ >> а для плоского освещающего пучка Е(г) и постоянной плотности w(z) = const получаем [2]:

Ф(г) = ф0 - JL in^c Vr2+(fo-cr2) 2  + 2c2r2 + 1-2 focj,       (2)

где c = и/а2, k = 2n/X.

Вычислительный эксперимент

Для исследования работы фокусирующих оптических элементов требуется рассчитать создаваемые ими в фокальной области световые поля. При этом необходимо принимать во внимание конечное разрешение б по плоскости ЭПО и конечное число уровней квантования фазы. При использовании для изготовления радиально-симметричных ЭПО фотопостроителей с круговым сканированием величина б определяется минимальной шириной кольца фотошаблона, то есть "размером пятна" фотопостроителя. Таким образом, принимаемая модель фазовой функции синтезируемого радиально-симметричного ЭПО имеет вид

N             г-г _ д

Ф(г) = 2 ф • rect(----2—2—) ,                                       (3)

р=1 Р            6

где

N = [а/б] - суммарное число колец разрешения на оптическом элементе;

Фр - значение фазы на р-м кольце разрешения (р=1,N);

а)б - радиус центра р-го кольца.

6 » X, воспользуемся для оценки комплексной амплитуды наблюдения (р, z), где р = V х²+у² (см. рис. 1), инте

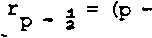
Считая, что w(p, z) в точке гралом Кирхгофа. При условии 2а « f0 можно показать [з] , что комплекс ная амплитуда поля w(p, z) вблизи базовой точки (р0, z) представляется в виде суперпозиции полей, созданных отдельными кольцами разрешения (гр-1/ гр), р=Гы:

где гр = Р-6, р=ТЛ; Lqz = V (fo + z)2+p^ ;

k а р

L =Vp2+f^ . о *       0

Одним из ющий функции Г € [г . ,Г 1

L р-1' PJ радиусом г

Р

способов вычисления интеграла (4) является метод, использУ" Ломмеля [4]. При этом поле от каждого кольца разрешения представляется в виде разности полей от двух отверстий и rp-i соответственно:

А N-1 ‘ w(p,z) Е Е(г 1) р=1    Р-5

ехр(1<рр)

- Е(гр+5) еХр (i ^l1

Wp(p,z) +

+ E(rN_l) . ехр(1фы) . wN(p,z),

где

wp(p,z)

комплексная амплитуда светового поля, созданного

в

точке

где

наблюдения отверстием радиуса г.

Как показано в работе [4], для wp(p,z)

k r2

w_p(p,z) = £ 2- exp[ik(L

oz

2      2

P - Pp 2L oz

ЧР

Un

, p=l,N. P

имеет место формула

exp (—^) • U,(qp, sp) 4

s2             i q.

- i exp (-J—) + exp( 4P

при

qD s р

2/ 1

Р

Loz

Lo

sp

exp (-

) Vo(qp

k r p

L oz

1 q

s ) p

)U2(q , s ) при

i q.

- exp (--—

Ч.

s р

и Vn

функции Ломмеля

K)Vi (qp

SP

Результаты вычислительного эксперимента

Алгоритмы расчета дифракционного интеграла реализованы в виде комплекса программ для ЕС ЭВМ, сопряженного с пакетом прикладных программ обработки изображений и цифровой голографии [5] и комплексом графических программ ГРАФОР. Осуществленный с помощью разработанного программного средства вычислительный эксперимент с фокусатором в тонкий продольный цилиндр на оптической оси выявил следующие характерные особенности распределения света:

• а)    вытянутая фокальная область с глубиной ~(0,7т0,9)и;

• б)    спад интенсивности к концам "отрезка фокусировки";

• в)    значительные перепады интенсивности вдоль отрезка [0, и], обусловленные дифракционными эффектами на кольцевой структуре фокусатора.

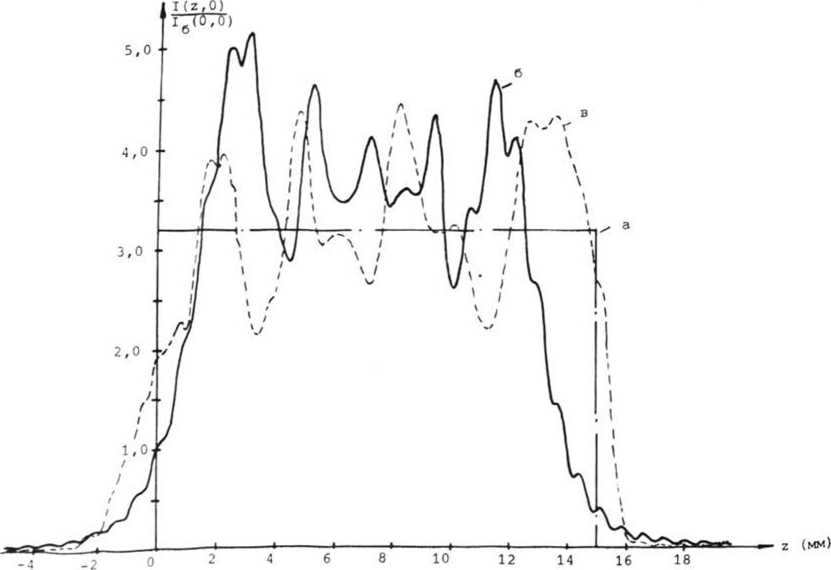
• 3. Распределение интенсивности I (z , 0)/I (0,0) вдоль оптической оси ^РИ а - "идеальный фокусатор", б - фокусатбр (2), в - фокусатор

На рис. 2 представлены изофоты распределения света в фокальной области фокусатора с повышенной глубиной фокуса с параметрами: fo = 300мм, X = 0,633 мкм, а = 12,8 мм, и = 15 мм, N = 128. График распределения интенсивности вдоль оптической оси для тех же параметров фокусатора -кривая б на рис. 3. Нормировка произведена на значение интенсивности в фокусе объектива. Среднеквадратичное отклонение интенсивности вдоль отрезка фокусировки" составляет 0,374, а максимальное отклонение д1/1 = 0,9, где I - среднее значение интенсивности вдоль отрезка.

Р (мм)

Фокальная плоскость

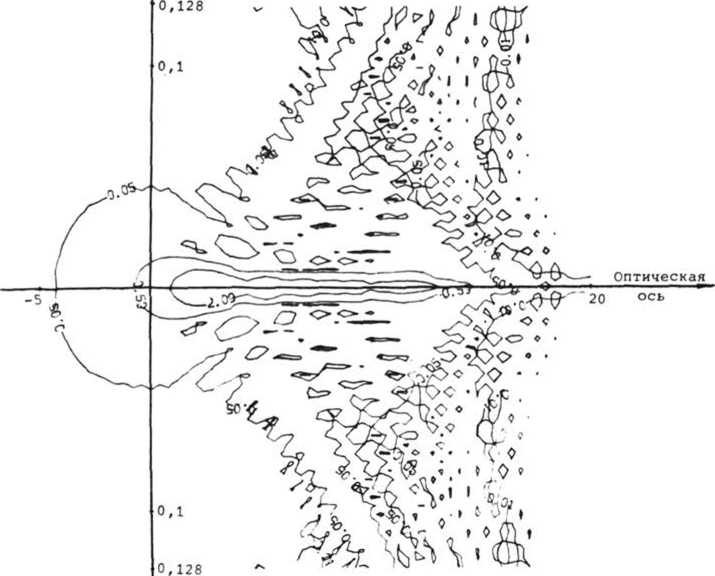
рис. 2. Изофоты трехмерного распределения интенсивности I(z,p)/I(0,0) в фокальной области фокусатора с повышенной глубиной фокуса и = 15 мм при fo = 300 мм, а = 12,8 мм, X = 0,633 мкм, N = 128

с корректированной фазовой функцией

Процедура корректировки

Анализ результатов вычислительного эксперимента приводит к необходимости корректировки фазовой функции фокусатора на основе полученных распределений интенсивности света. Для этого разработан алгоритм и написана программа расчета оптического элемента, концентрирующего излучение в тонкий продольный цилиндр на оптической оси с заданным распределением энергии вдоль него. Алгоритм расчета построен на численном решении системы (1) для произвольного w(z). Реализованная итерационная процедура корректировки фазовой функции фокусатора заключается в формировании нового w(z) на основании данных вычислительного эксперимента на предыдущем шаге:

wk+l(z) = wk(z^ + h'(Ik ~ Xk(z'0))' zt [0,и].

при расчете фокусатора на к-той (к+1-й) итерации; Ik(z,0) и 1^ - полученные в результате вычислительного эксперимента на к-той итерации соответственно распределение интенсивности и среднее значение интенсивности вдоль отрезка [0,и]; h - оптимизируемый параметр, выбирается таким образом, чтобы минимизировать среднеквадратичное отклонение интенсивности вдоль отрезка ek+l ~ ^

/ dk+1 - Ik+1(z,0))2dz

Исследователь может вмешиваться в ход вычислительного эксперимента, прерывая его в случае появления на экране дисплея приемлемого результата. Кривая в на рис. 3 - распределение интенсивности, полученное в результате трех шагов итерационной процедуры. При снижении среднего уровня интенсивности с 3,21 до 3,05, то есть менее чем на 5%, достигнуто среднеквадратичное отклонение интенсивности 0,26 и максимальное отклонение интенсивности от среднего Д1/1 = 0,53.

Заключение

Вычислительный эксперимент, основанный на предложенных дифракционных соотношениях и разработанных программных средствах, позволяет не только визуализировать и количественно проанализировать сложные распределения светового поля от плоских оптических элементов, но и создать корректирующую процедуру для оптимизации фазовой функции фокусатора с повышенной глубиной фокуса.

Результаты вычислительного эксперимента позволяют перейти к синтезу соответствующих ЭПО и их экспериментальному исследованию в оптической системе.