Procedure for Processing Biometric Parameters Based on Wavelet Transformations

In modern conditions, the development of covert monitoring tools (CMT) of the person and emotions of operators of information management systems (IMS) based on biometric parameters is one of those tasks, the solution of which will significantly increase the effectiveness of detection of unauthorized access to information and the effectiveness of adequacy assessment. psycho-emotional state of staff regarding the possibility of solving their functional responsibilities [1-3]. These tools are successfully used in office information systems for protection against insiders, in distance learning systems for automatic control of the mode of submission of educational materials and to verify the authenticity of the student's identity when passing exams. In addition, remote automatic monitoring of emotional state can be useful in systems for detecting law and order in public places and in information systems for automatic monitoring of psycho-emotional state of patients.

In most cases, the theoretical basis of the CMT of personality and emotions is a neural network analysis of such biometric parameters as facial images and iris images, ie biometric parameters that correlate with two-dimensional images and are characterized by geometric indicators [1, 3, 4]. This is due to the availability of registration tools, high affinity of these biometric parameters with the identity and emotions of person , proven neural network solutions and the availability of available representative labeled databases of facial images and iris images, which greatly simplifies the process of developing neural network models. However, in practice, the effectiveness of CMT largely depends on the quality of registration of the image of the face and the image of the iris, which is explained by the presence of typical obstacles that can not be eliminated by improving the characteristics of hardware [1, 2, 5, 6].

Thus, it explains the relevance of the scientific and practical problem of improving the methods of filtering biometric parameters, which are correlated with two-dimensional images and used in biometric neural network CMT of the person and emotions of IMS operators.

2.    Related Works

As shown by the results of the analysis of scientific and practical work [5, 7, 8], one of the main directions of development of neural network means of recognizing a person's face and emotions on the face and iris is to increase the adaptability of these tools to expected operating conditions. However, in [6, 9-12] it was noted that typical interferences that significantly complicate the recognition process are mainly caused by:

• •    The presence of objects that cover part of the image.

• •    Uneven lighting, which leads to glare in the image.

At the same time, in many cases the localization and other parameters of typical interference are non-stationary dynamic in nature. For example, in Fig. 1-3 it is shown images of the iris and images of a person noisy under the influence of typical interference. In Fig. 1-3 it is shown the interference, which includes glare, glasses and a microphone. Note that, despite the nature of the noise, their negative impact is that areas appear in the image that actually distort the image. To level such influence in works [11-15] it is offered to use various methods of local filtering and segmentation of images.

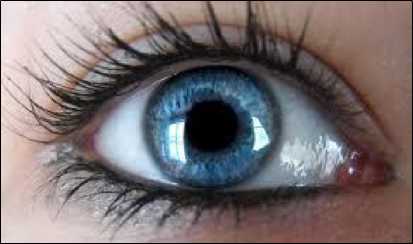
Fig. 1. The image of the iris, noisy with glare

Fig. 2. The image of a man's face with glasses

Fig. 3. The image of a human face covered by a microphone

A critical review of such filtering and segmentation methods is given in works [15, 16]. It is noted that as a result of filtering, the brightness characteristics of each point of the digital image are replaced by another brightness value, which is less distorted by the obstacle. The filtration methods are divided into:

• •    Spatial.

• •    Frequency.

Spatial image filtering methods involve the representation of a raster image in the form of a two-dimensional matrix, which allows the application to each point of the image of the convolution operation. Thus, in [17] the method of cleaning from noise due to the use of smoothing filters for cleaning images in shades of gray. The comparison of efficiency of different types of smoothing filters was conducted. Computer experiments have shown that a 5 × 5 Gaussian filter is the most effective for low-noise images. It is noted that spatial filtering methods can be effectively used to improve image quality, but their use is ineffective for eliminating interference caused by distortion of the image. In this case, frequency filtering methods are considered more effective.

Classical frequency filtering methods are based on spectral analysis of images using a discrete Fourier transform. The disadvantages of such methods are caused by the limitations of the Fourier method, which lead to the difficulty of localizing the frequency parameters of the spectrum over time [18, 19].

Correction of this shortcoming is associated with the use of filtering methods based on wavelet transforms [19, 20]. For example, in [21] a mathematical model of parameterization of the structure of the iris of the eye using wavelet transform based on derivatives of the Gaussian function is considered. The results of experimental researches proving efficiency of the offered model are shown.

In works [22-25], which are devoted to the analysis of ways to use wavelet transforms in the field of image coding, a list of requirements is defined, the implementation of which ensures the effectiveness of this process. These requirements are correlated with the possibility of:

• •    Multi-scale image analysis,

• •    Spatial localization,

• •    Orthogonality,

• •    Implementation of a computational algorithm with low computational complexity,

• •    Use of proven tools.

Analysis of [20, 24-27] suggests that in most cases as a basic wavelet in image filtering use wavelets HAAR, MHAT, WAVE, FHAT, GABOR, Daubechies wavelet, which are defined by expressions of the form (1-6)

1, х е [0,0.5]

Ф(х) = ]-1, хе [0.5,1]

(  0, х ^ [0,1]

ф(х) = ^тт-0,25(1 - х2)е-0,5*2,(2)

ф(х) = хе-0,5*2,(3)

f ''ЛЕ ' Z'-|

ф(х) =  -0.5,хе[1,1]

к 0,х е [1,“]

ф(х) = е-(*-*о)2/а2е—‘ко(*-*0),

ф(х) = ^^кЭкФ^хк).(6)

In this case, to select the most effective type of basic wavelet, it is possible to use the approach proposed in [20]:

if E_h = тах{Е 1 ,Е 2 , ^E_D] ^ ф_к = ф_е//,

Ed = EU

^ v ^e d,v ,

where E_d is the efficiency of the d-th type of the basic wavelet, V is the number of efficiency criteria, a_P is the weighting factor of the v-th efficiency criterion, е_йу is the value of the v-th efficiency criterion for the d-th type of the basic wavelet, D is the number of valid types of basic wavelets, ф_е // - the most effective type of basic wavelet.

The results of the analysis suggest that although many works have been devoted to the application of wavelet transforms in the field of image filtering, the application of the obtained results for filtering biometric parameters, which are characterized by geometric indicators, is complicated by the need for complex adaptation to nonstationary dynamic changes. It is possible to correct this shortcoming, by analogy with [20], by developing a procedure for applying wavelet transforms to filter these parameters, which determines the purpose of this study. Thus, the purpose of this study is to develop a procedure for filtering biometric parameters, which through the use of wavelet transform technology will clean the image of the face and the iris of the eye from typical non-stationary interference.

3.    Development of the Mathematical Apparatus

The biometric parameter, which is characterized by geometric indicators, is essentially a digital image, which is a discrete two-dimensional signal. According to the recommendations [24, 28], it is advisable to represent the following signal using a two-dimensional rectangular or square matrix of the form:

^в м = ||

х1,1  хи х/1  хЦ х/,1 хЫ

ха

(R,G,B)i,i

S rgb = П⁽^, ^G,^B) ;,1 (R,G,B) j,i

(R,G,B)1,t (R,G,B)j,t (R,G,B)],l

(R,G,B) 1, _;

(R,G,B)jJI (R,G,B)_}J

where S_M is a monochrome image, , S_RGB is an image in RGB format, I is the width of the image, J is the height of the image, x^ is the value corresponding to the color of the monochrome pixel with coordinates ( i , j ), (R,G,B) j^ -components of RGB pixel color channels with coordinates ( i , j ).

Therefore, for the analysis of such signals it is accepted to use two-dimensional discrete wavelet transform, which is a composition of one-dimensional discrete wavelet transforms. In general, for one line of pixels of a monochrome image, the direct one-dimensional discrete wavelet transform is determined by expression (11), and the inverse wavelet transform is determined by expression (12).

[W^k = 7^Z^-o1(x„^*(a^xn - k))

,

1 < m, k < N

q(xn) =     Щ Z^=-1(^*(xn)Wm^),

m(aQj where a0 is the initial scale, k is the offset parameter, m is the scale parameter, xn is the color of the nth point of the image, * is the operation of complex conjugation, N is the image size, φ is the basic wavelet of the form (1-6).

At each stage of detailing, first one-dimensional discrete wavelet transforms are applied to each row of the twodimensional matrix of input data (9, 10). After that, one-dimensional wavelet transforms are performed for each column of the obtained matrix.

The mathematical apparatus for calculating the matrix of wavelet coefficients of the j-th row of pixels of a monochrome image is determined by expressions of the form:

|W(j)^k

^

In=1o(x(j')n^*(a™x(j')n

- k))

1 < m,k < J

where J is the height of the image, x(J)_n is the value of the encoded color of the image of the n-th pixel, j is the line number of the pixels.

The mathematical apparatus for calculating the matrix of wavelet coefficients of the j-th row of pixels of a color image is determined by expressions of the form:

।W(j)^k

= ЛЩШЧаЖ - k))

JaQ¹                                      ,

1 < m, k < J

q(j)n = 0,299R(j)n + 0,587G(j)n + 0,114B(J)n,

where q (j")_n is the value of the encoded color of the image of the nth pixel, R , G , B are the components of each of the color channels in RGB format for a single pixel.

Note that the expressions (14, 15) are used in the case when the image processing color can be neglected.

In case it is not expedient to realize it, wavelet coefficients are calculated separately for each of color channels. The corresponding mathematical apparatus can be written as follows:

|W(j)^k = -^^ (q(j')1,n^*(a01q(j')1,n - k))

1 < m, k < J where q (j")ln is the intensity of the l-th color channel for the n-th pixel located in the j-th line of pixels.

When using the RGB model, the channels are correlated with red, green and blue.

Actually, the filtering procedure means removing certain components of the matrix W _m,k . In most cases, those components of the matrix W _m,k for which the offset parameter and/or the scale parameter are outside the predetermined range are removed.

After that, the components of the filtered matrix W m,k are used in the procedure of inverse wavelet transform to restore the cleared image. Expression (17) is used for a monochrome image, and expressions (18, 19) are used for a multicolor image.

x(Dn=  ^  En-=1oEk"=1o(^*(x(j-)n)W(j-)m,k),

^Ln(a Q )

qOX = -^^Z, _n =¹o ^Z _k =¹o(p^^^                                        (18)

ш⁽а о )

Ч() 1д =   Z^ o Z k-^ CqUWWUW                 (19)

ш(а0)

Note that expression (18) is used when the image color channels can be integrated with each other, otherwise expression (19) is used.

Based on the requirements formed in [20, 23,25], which ensure the efficiency of wavelet transforms, the expediency of using dyad discrete wavelet transform is determined, which reduces the computational complexity of the procedure for calculating wavelet coefficients by reducing the number of copies of the basic wavelet. The use of dyad discrete wavelet transform leads to the modification of expressions (13, 14, 16-19):

{

(W(j)^k = ^(хОХрКхОХ - k)) (              1 < m, k <  I	(20)
(W(j)^k = ^s Z ^-= 1 o (q(7') „ P * (a m q(j-) „ - k)) I              1 < m,k < I	(21)
W(j)l№ k = v^Z n - =1> (q(jW(a m q(j\ ,n - k)), 1 < m, k < I	(22)
X(j') ^ = ^Z ^ - = 1 o ZI k - = 1 o (P * (x(j-)n)W(V-) m,k ),	(23)
q(j') " = ^Z n- 1 o ZI k■= 1 O (P * (q(7■) n )W(7■) m,k ),	(24)
q(v')i ," = ^ZI;-; o Z k-o (p ' (q(;) „ )W(;); .m.k ).	(25)

The difficulty of creating effective filters is largely due to the difficulty of calculating the limits of the ranges that determine the list of components of the matrix W _m,k to be extracted. This is due to the dynamic nature of the interference for the same object at different times during the registration of biometric parameters. For example, as shown in Fig. 4, at time t ₁ in the lower left corner of the iris, there arises a "glare" type of noise due to uneven lighting. At time t ₂ due to a change in lighting, such a disturbance occurs in the upper right corner of the iris. Similar dynamic distortions are observed when registering an image of a human face.

At the same time, the dynamic nature of the localization of one or more interferences allows to claim that at any given time on the registered image can be both distorted and undistorted parts of the image, which is associated with the biometric parameter. Herewith the location of these parts changes. Thus, potentially using images recorded at different times, it is possible to reproduce a noiseless image.

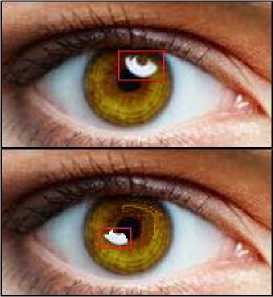
Fig. 4. Illustration of the dynamic nature of the localization of interferences

This postulate allows to propose an approach to the development of a method for filtering biometric parameters. In the basic variant, the approach involves calculating the values of the wavelet coefficients of each of the registered images, pairwise integration of the calculated values of the wavelet coefficients with each other and the implementation of the inverse wavelet transform, which leads to a filtered undistorted image.

Note that the pairwise integration of wavelet coefficients, carried out taking into account the need to eliminate interference, can be implemented using one of the principles:

• •    'max' - selection of the maximum of two coefficients;

• •    'min' - selection of the minimum of two coefficients;

• •    'mean' - selection of the average value from two coefficients;

• •    'img1' - selection of the coefficient of the first image;

• •    'img2' - selection of the coefficient of the second image;

• •    'rand' - random selection of two coefficients.

An example of face image filtering, implemented in accordance with the above approach using the software MATLAB, is shown in Fig. 5. The results of the experiments confirmed the data [21-28] on the significant dependence of the quality of filtering of biometric parameters on the type of basic wavelet. Thus, in Fig. 5 ellipse highlights a part of the image of a human face, reproduced with unsatisfactory clarity after filtering using a basic wavelet type Daubechies wavelet-5.

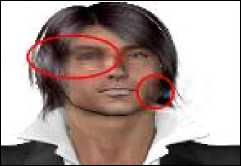
Fig. 5. Example of filtering a face image using MATLAB

Therefore, the filtering procedure it is used the results of [20], which presents an approach to selecting the most efficient basic wavelet, which meets the need to achieve sufficient accuracy of spectral analysis with minimal computational costs and is described by expressions (7, 8). To determine these expressions formed, given in table. 1 list of efficiency criteria of the basic wavelet type.

Table 1. Performance criteria of the basic wavelet type

Criterion	Description
e 1	Existence of redundant information in wavelet coefficients
e 2	Computational complexity
e 3	The ability to implement fast wavelet transform
e 4	Presence of infinite regularity
e 5	Presence of random regularity
e 6	Symmetry of the basis function
e 7	Availability of proven tools for implementation
e 8	Orthogonality of the basis function
e 9	Presence of scaling function
e 10	Full signal recovery capability
e 11	Compactness of the basis function
e 12	Similarity of the geometry of the basis function with the geometry of the analyzed process

Considering the results [20, 25], it is accepted that in the basic version, the values given in table 1 of the criteria from e ₁ to e ₁₁ can be evaluated on a two-point discrete scale. In this case, for the d -th type of the basic wavelet, the value of the v -th criterion is equal to 1, if the corresponding v -th requirement is fully met, and, is equal to 0, if not met. The calculated values of the criteria for the tested types of basic wavelets are given in table 2.

Table 2. The value of performance criteria for the tested types of basic wavelets

Criterion	Type of basic wavelet
	HAAR	MHAT	FHAT	WAVE	DB
e 1	1	0	1	0	1
e 2	1	1	0	0	0
e 3	1	0	1	0	1
e 4	0	1	0	1	0
e 5	0	0	1	0	1
e 6	1	1	1	1	0
e 7	1	1	1	1	1
e 8	1	0	0	0	1
e 9	1	0	0	0	1
e 10	1	0	1	1	1
e 11	1	1	0	0	1

It should be noted that a priori to determine the value of the efficiency criterion e 12 , which correlates with the similarity of the geometry of the basic wavelet with the geometry of the analyzed biometric parameter, is quite difficult. Therefore, in table 2 the value of this criterion is missing.

Based on the proposed approach and results [1, 4, 20], a procedure for filtering biometric parameters associated with two-dimensional color or monochrome images has been developed. In the basic case, the implementation of the procedure is to perform the following steps:

• 1.    Register a video sequence that corresponds to the sequential display of images that are associated with a certain biometric parameter.

• 2.    Identify a list of typical obstacles that are inherent in certain biometric parameters.

• 3.    Determine the need for analysis of color, monochrome (with one color channel) or black and white image.

• 4.    Determine the list of controlled images in the video series that correspond to the images in which the distortions are localized in different parts.

• 5.    Implement the selection of the most effective basic wavelet. For this:

• •    Expertly determine the significance of each of the performance criteria from table 1.

• •    Expertly determine the value of criterion e12.

• •    Using expression (8) to calculate the efficiency of each type of basic wavelet.

• •    Using expression (7) to determine the most effective type of basic wavelet.

• 6.    Using expressions (14-16, 20-22) to calculate the values of wavelet coefficients of each of the controlled images with minimal detail of wavelet transforms.

• 7.    Choose the principle of integration of wavelet coefficients.

• 8.    Integrate the calculated values of the wavelet coefficients in pairs.

• 9.    Using the obtained values of the wavelet coefficients, with the help of expressions (17-19, 23-25) implement the inverse wavelet transform, which produces noiseless image.

• 10.    Expertly determine the quality of the obtained filtered image. If the quality is sufficient, the procedure is considered complete. Otherwise, the level of detail of wavelet transforms should be increased.

The peculiarities of this procedure are due to the fact that:

• •    When implementing the second and third stages should take into account the peculiarities of the task of recognizing biometric parameters.

• •    An example of the program code for the wavelet coefficient integration procedure is shown in Listing 1. The MATLAB programming language is used.

Listing 1

map=colormap(pink);

X2 = rgb2ind(mimg1,map);

XFUS = wfusimg(X1,X2,'db3',9,'min','min')

The program provides:

• •    Reading face1.bmp and face2.bmp files.

• •    Using Daubechies wavelet-3 as a basic wavelet.

• •    The level of detail of the wavelet transform is equal to nine.

• •    When integrating wavelet coefficients, the smaller of the two coefficients is selected.

Experiments aimed at studying the proposed procedure when used to clean the image of the face and iris are carried out. The research focuses on the choice of the basic wavelet.

Assessment of the significance of each of the efficiency criteria in the task was implemented using the expert method of pairwise comparison. The results obtained are shown in table 3.

Table 3. Weights of efficiency criteria of the basic wavelet type

e 1	e 2	e 3	e 4	e 5	e 6
0,11	0,2	0,06	0,06	0,06	0,06
e 7	e 8	e 9	e 10	e 11	e 12
0,06	0,06	0,06	0,11	0,06	0,1

Expertly obtained values of the criterion e ₁₂ are given in table 4.

Table 4. The value of the e12 criterion for the tested types of basic wavelets

HAAR	MHAT	FHAT	WAVE	DB
1	0	0	0	0

The calculation of the integrated efficiency index of each of the tested types of basic wavelets is implemented by substituting the data of table 2-4 in expression (8). The results obtained are given in table 5.

Table 5. The value of the integrated efficiency indicator for the tested types of basic wavelets

HAAR	MHAT	FHAT	WAVE	DB
0,88	0,44	0,46	0,29	0,58

Using expression (7), it was determined that HAAR is the most effective.

Determining the most effective type of basic wavelet allowed to conduct numerical experiments aimed at verifying the obtained solutions by checking the quality of filtering such biometric parameters as the image of the face and the image of the iris. Filtration is implemented using the MATLAB software package.

Rectangular monochrome and color raster images of the face with a size of 937 by 689 pixels, written in bmp files, were studied. The size of raster images of the iris is 184 by 274 pixels. The color of the image is written in RGB format. Obstacles in facial images are correlated with the presence of objects that partially overlap the image, and interference in the images of the iris - with glare due to uneven lighting. For clarity in Fig. 5 and in Fig. 7 obstacles in the images are highlighted by rectangles. For example, in Fig. 6 shows a noisy and filtered image of a face using a HAAR wavelet. Since in Fig. 6 the color of the noise was darker than the color of the face image, then in the process of integration, the larger of the two wavelet coefficients was chosen.

Fig. 6. Example of face image filtering using HAAR wavelet

Fig. 7 illustrates the application of the proposed procedure for filtering the image of the iris.

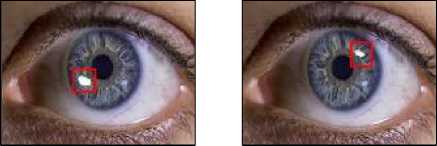
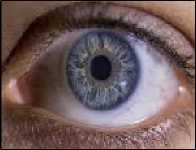
Fig. 7. Example of filtering the image of the iris using a HAAR wavelet

In the case of filtering the iris of the eye, the color of the noise was lighter, so in this case, the smaller of the two wavelet coefficients was chosen. Note that in the above examples, the level of detail of the wavelet coefficients was equal to 1. Expert evaluation of the obtained filtered images showed a satisfactory filtering quality.

Experiments were also performed in which other types of basic wavelets were used for image filtering. It is determined that their use led to at least a twofold increase in the number of computational iterations and/or to poor filtering, which is illustrated in Fig. 5. Thus, it is experimentally confirmed that from the standpoint of sufficient accuracy and computational complexity of filtering, the most effective is the use of HAAR as a basic wavelet. It is sufficient to implement a wavelet transform with a level of detail equal to 1.

Thus, the results of experiments confirm the feasibility of the proposed method for filtering biometric parameters correlated with two-dimensional monochrome or color images. However, the step of the procedure related to the automatic selection of the method of integration of wavelet coefficients, which is used to level the interference localized in different places of the image associated with the biometric parameter, needs to be refined.

4.    Conclusions

The problem of the article is related to the improvement of the means of covert monitoring of the face and emotions of the operators of information and control systems on the basis of biometric parameters that correlate with two-dimensional images and are characterized by geometric indicators. The difficulty in developing such tools has been shown to be largely due to the cleaning of images associated with biometric parameters from typical non-stationary interference caused by uneven lighting and foreign objects that interfere with video recording.

The prospects of means of cleaning from disturbances on the basis of wavelet transformations are defined. The approach to the development of the procedure of filtering biometric parameters is substantiated, which involves calculating the values of the wavelet coefficients of each of the registered images, pairwise integration of the calculated values of the wavelet coefficients and the implementation of inverse wavelet transform, which leads to filtered undistorted image. An approach to selecting the basic wavelet used for image filtering is also proposed.

A filtering procedure has been developed, which, due to the application of the proposed approaches, allows to purify biometric parameters such as facial images and iris images from typical non-stationary interferences with satisfactory quality using a minimum amount of computing resources. The conducted experimental researches have shown expediency of application of the developed procedure for filtering of typical interferences on the images associated with biometric parameters of operators of information and control systems.

It is proposed to correlate the ways of further research with the choice of the method of integration of wavelet coefficients, which is used to level the interference localized in different places of the image associated with the biometric parameter.