Процесс формирования компактов

Машиностроение и машиноведение

Введение. Биомасса — это все возобновляемые за короткое время органические материалы. Биомасса используется в качестве продовольствия, для приготовления кормов, получения энергии. Биомасса относится к дисперсным материалам, характеризуемым высокой пористостью, т.е. низкой плотностью, что вызывает неудобства в ее использовании. Поэтому для улучшения технологических свойств ее подвергают уплотнению, с приданием определенной формы компактам (брикетам, гранулам и др.). Помимо повышения транспортабельности, обеспечиваемой за счет уплотнения биомассы, обеспечивается получение и других полезных свойств. Например, гранулирование комбикормов обеспечивает сохранность рецептуры кормов при хранении и скармливании животным, повышение питательности кормов и увеличение их скармливаемости (на 20% больше, чем рассыпных). Использование биомассы в виде компактов из опилок обеспечивает улучшение экологии за счет сокращения площади свалок, позволяет получать новый продукт — топливные гранулы, которые могут являться заменителями угля, причем без нанесения ущерба окружающей среде.

Целью настоящей работы является разработка методики расчета пресса-гранулятора с кольцевой матрицей, учитывающей весь комплекс факторов, действующих при работе этой машины.

Материалы и методы. Расширение производства компактов из биомассы вызвало значительный интерес к созданию конструкций машин для производства компактов. В трудах [1–5] разработаны методики определения отдельных параметров этих машин, но целостная методика расчета их конструктивных и технологических параметров пока не создана. Это не гарантирует эффективность использования новых машин при производстве компактов из различных видов биомассы. Поэтому предпринята попытка разработки методики, учитывающей весь комплекс факторов, действующих при работе машин. При анализе технологического процесса использовались методы, разработанные в механике грунтов [6], теории обработки материалов давлением [7], сельскохозяйственном машиностроении [1, 8].

Результаты исследования. Для получения гранул в основном применяются прессы с кольцевыми матрицами, обеспечивающие непрерывность процесса формирования. В процессе уплотнения происходит изменение состояния дисперсного материала — из рассыпного он превращается в монолитное тело, обладающее новыми характеристиками. Под действием внешнего давления р происходит изменение плотности дисперсного материала ρ и его структурно-механических свойств — внутреннего и внешнего трения, коэффициента бокового давления ξ = dq / dp , сцепления τ 0 , структурной прочности:

Р стр = ^{2 T} O cos ^{/ ( 1} - SW )

где ф — угол внутреннего трения материала.

Структурная прочность — это прочность внутренних связей между частицами дисперсного тела. Деформации до преодоления структурной прочности незначительны и обратимы. При нагрузке, превышающей структурную прочность, связи между частицами нарушаются, они перемещаются относительно друг друга и начинается уплотнение. При этом на стенки камеры прессования начинает действовать боковое давление.

Боковое давление на стенки камеры прессования при уплотнении материала возникает не сразу, а только после достижения давлением р величины, равной структурной прочности материала q = '^p - p стр).

То есть боковое давление при уплотнении определяется только частью внешнего давления р , превышающего структурную прочность материала при сжатии.

График изменения бокового давления от осевого при уплотнении и разгрузке показан на рис.1. Экспериментальная зависимость при нагружении представлена пунктирной линией. Криволинейный характер зависимости свидетельствует о том, что при уплотнении материала его свойства непрерывно меняются. Касательная, проведенная к кривой в точке максимального нагружения, наклонена к оси абсцисс под углом, тангенс которого равен коэффициенту бокового давления при максимальном нагружении и отсекает на оси абсцисс отрезок, равный структурной прочности материала р _стр. При дальнейшей разгрузке и повторном приложении нагрузки значения этих показателей сохраняются.

Если при нагружении внутреннее трение препятствует деформации, и, следовательно, уменьшает боковое давление, передаваемое на стенки камеры уплотнения, то при разгрузке внутреннее трение препятствует расширению уплотненного материала. Поэтому уменьшение давления р не ведет к уменьшению бокового давления до тех пор, пока касательные напряжения не уменьшатся на величину, равную величине напряжений начального сдвига ∆τ = τ н .

С учетом изменения знака касательных напряжений, зависимость бокового давления q от внешнего р для второго этапа разгрузки имеет вид:

q = ^kp+p стр )=^ p+q о где qо = ^рстр — остаточное боковое давление.

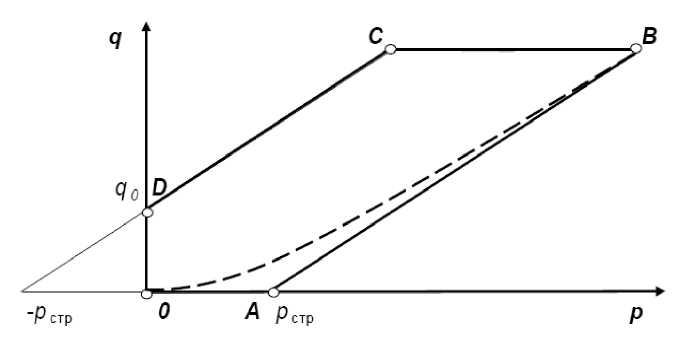
Рис.1. Зависимость бокового давления q от осевого р при уплотнении (экспериментальная зависимость: начальное нагружение 0В, теоретическая зависимость — линия 0АВ, разгрузка — линия ВС D )

Fig.1. Dependence of lateral pressure q on axial p under compaction

(observed dependence: initial loading OB, theoretical dependence – line OAB, unloading – line BCD)

При разгрузке боковое давление не изменяется до тех пор, пока внешнее давление не уменьшится на величину 2 р _стр от начального значения. Затем боковое давление понижается до значения остаточного бокового давления.

Уравнение, связывающее приложенное давление и плотность (или пористость) уплотняемого материала, названо Мельниковым С. В. «основным уравнением прессования» [9].

Многочисленными исследователями предложены различные математические зависимости для описания этого процесса. Особов В. И., проанализировав работы предшествующих исследователей, установил, что все раннее полученные зависимости имеют недостатки и высказал гипотезу о закономерности процесса сжатия сеносоломистых материалов [1]. На основе этой гипотезы теоретически получено уравнение, связывающее плотность уплотненного материала с давлением, необходимым для получения этой плотности:

p = C(e“ (р-р 0)-1)                                        (1)

где ρ 0 — начальная плотность материала; С, a — эмпирические коэффициенты.

Коэффициенты С и a в формуле (1) не имеют четкого физического смысла [9], что приводит при пользовании этой формулой к ошибкам и неверным выводам. Например, Яговкин П. В. делает заключение, что чем выше начальная плотность материала, тем меньшее давление необходимо для его уплотнения до одинаковой плотности [10]. Однако, как свидетельствует опыт, для достижения одной и той же плотности компакта, независимо от начальной плотности уплотняемого материала, к нему необходимо приложить одно и тоже давление. Кроме того, из формулы следует, что при изменении давления на некоторую величину происходит соответствующее изменение и плотности материала. Экспериментальные исследования свидетельствуют о том, что пока давление не превысит структурную прочность материала p _стр его уплотнения, появление необратимых изменений его пористости не произойдет [6]. Также очевидно, что плотность материала при уплотнении не может превысить плотность составляющих его частиц. Однако из приведенной выше формулы этого явно не следует.

Увеличение внешнего давления приводит не только к уменьшению пористости дисперсного материала, но и к увеличению числа контактов между частицами, увеличению прочности связей. Поэтому для осуществления уплотнения необходимо к телу прикладывать все большее и большее давление.

При уплотнении дисперсного материала приращение внешнего давления dp пропорционально его прочности σ s и изменению его пористости d П:

dp = - ас s d n                                     (2)

где α — коэффициент пропорциональности.

Предел текучести σ s , согласно теории Мизеса Р. [11], равен интенсивности напряжений, т.е. σ s = р – q .

При нагружении q = ^( р - р _стр). После подстановки значений в формулу (2) и решения получим:

Машиностроение и машиноведение

^p стр p=

1 - ^

' J ¹ -о ( По ^- П )

)

- ^

где П0 — начальная пористость дисперсного материала

Поскольку пористость П = 1 - р/рт, где р — плотность материала, рт — плотность частиц материала, последнее выражение можно представить в виде:

где a = а (1- ^), C = p ср. /(1- £).

Полученное выражение (4) учитывая, что значения коэффициента бокового давления не могут превышать единицу, практически полностью совпадает с уравнением (1). Однако коэффициенты обретают физический смысл: коэффициент С характеризует сопротивляемость материала уплотнению, коэффициент а — интенсивность изменения внешнего давления.

Задаваясь значением необходимой плотности компакта, определяется максимальное давление уплотнения. Регулировка давления в прессах осуществляется изменением длины канала.

Длина канала прессования, обеспечивающая необходимое давление на входе, определится по формуле [9]:

)

L= ^s ln ^{p max} +1 ^f  ( Р стр    )

где 5 — площадь поперечного сечения канала, и — периметр поперечного сечения канала, f — коэффициент трения материала о стенки канала.

Если длина канала получается большой, то в начале канала рекомендуется выполнять предкамеру.

Уплотнение в прессах осуществляется не только за счет сопротивления канала, но также на перемычках матрицы между каналами. Первоначальное уплотнение осуществляется на всей поверхности матрицы, которая на этом этапе может рассматриваться сплошной. С учетом упругости материала, ранее запрессованного в каналы, при повышении нагрузки происходит его упругая деформация, вследствие чего уплотнение новой порции материала осуществляется на упругом основании. Это снижает интенсивность возрастания давлений в конце этапа уплотнения материала — вогнутая кривая зависимости давления от высоты слоя уплотняемого материала (рис. 2) получает перегиб (точка В) и становится выпуклой.

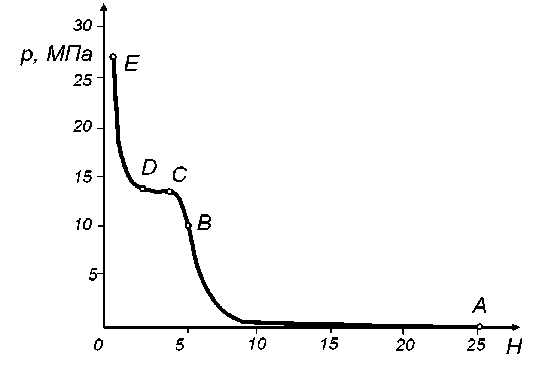
Рис. 2. Зависимость давления от высоты слоя материала при продавливании через перфорированную поверхность

Fig. 2. Dependence of pressure on layer height of material when pressing through perforated surface

На новых матрицах эти перемычки выполнены плоскими, вследствие чего с них затруднено сталкивание материала в каналы.

Дальнейшее повышение давлений в зоне прессования при уплотнении материала приводит к преодолению противодавления каналов рт и в них начинает проталкиваться материал, находящийся непосредственно над каналами. Таким образом начинается первая стадия процесса продавливания.

Под действием разности давлений, действующих над перемычками и каналами, нарушается предельное равновесие материала, находящегося на перемычках, и последний начинает стекать в каналы по площадкам сдвига. Эта стадия процесса продавливания происходит при постоянном давлении. Однако, для части материала, ограниченной площадками сдвига материала и плоскостью перемычек (жесткое ядро АВС, рис.3), сдвиг затруднен.

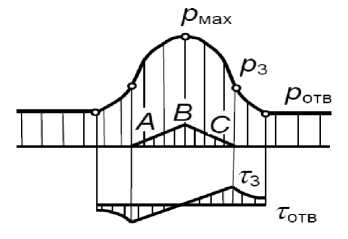
Рис. 3. Распределение давлений прессования и касательных напряжений на перемычках между каналами при продавливании ( АВС — жесткое ядро на перемычке, р _отв — давление над отверстиями, р _мах — максимальное давление на перемычке, τ _з — касательные напряжения на перемычке)

Fig. 3. Distribution of compacting pressures and tangential stresses on bridges between channels under forcing (ABC – rigid core on the bridge, р_отв – pressure above holes, р_мах – maximum pressure on bridge, τ ₃ – tangential stresses on bridge)

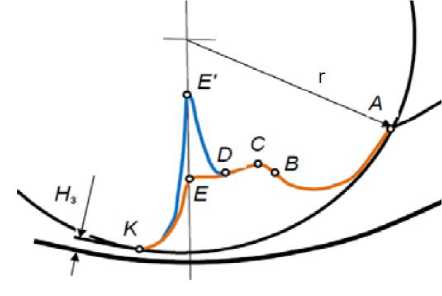
Рис. 4. Распределение давлений в зоне прессования в прессе с кольцевой матрицей: ABCDEK — при выполнении перемычек матрицы плоскими; ABCDE′K — при выполнении перемычек матрицы наклонными; Н _з — толщина слоя, напрессованного на рабочей поверхности матрицы

Fig. 4. Pressure distribution in compacting zone in press with ring die: ABCDEK — when matrix jumpers are flat; ABCDE'K — when executing matrix jumpers are oblique; H₃ — thickness of layer pressed on matrix working face

На второй стадии продавливания, когда расстояние между рабочими органами становится меньше высоты жесткого ядра образованного на перемычках матрицы (рис. 3), происходит резкий рост давления

(рис. 4, кривая DЕ' ) , значительно превышающий противодавление каналов. Таким образом, давление в рабочей зоне определяется не только противодавлением каналов матрицы, но и сопротивлением перфорированной поверхности матрицы. Среднее значение давлений в зоне проталкивания составит:

^p пр

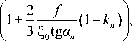
где k п — коэффициент перфорации матрицы, α н — угол наклона площадок сдвига.

Величину максимальных давлений, действующих на второй стадии продавливания, можно регулировать величиной зазора, устанавливаемого между рабочими органами пресса — чем больше зазор, тем меньше давление, действующее на перемычках.

Если зазор между рабочими органами пресса устанавливать бо́льшим, чем формируется высота жесткого ядра, то вторая фаза продавливания, характеризующаяся высокими давлениями, будет отсутствовать. Однако при большой величине зазора на поверхности матрицы образуется толстый напрессованный слой материала, на повторное сжатие которого затрачивается значительная часть энергии. Это приводит к снижению производительности пресса, сильному износу вальцов, вследствие их проскальзывания, и

Машиностроение и машиноведение

измельчению материала.

Следует отметить, что сказанное относится к новым матрицам, имеющим плоские перемычки между каналами. При эксплуатации за счет износа перемычки приобретают наклон в сторону входа в каналы. На наклонной перемычке зона застоя образоваться не может. Вследствие этого исключается вторая стадия продавливания. В результате условия сталкивания материала в каналы облегчаются, снижаются действующие усилия прессования, уменьшается энергоемкость процесса.

Предлагается такие наклонные перемычки выполнять с помощью конических углублений на поверхности матрицы, причем вершина образующего конуса лежит в пределах отверстия матрицы, а радиус бо́льшего основания образующего конуса равен расстоянию от точки, равноудаленной от центров трех соседних отверстий. При таком выполнении рабочей поверхности матрицы все площадки оказываются наклоненными в сторону отверстия, облегчаются условия проталкивания материала через перфорированную поверхность, что позволяет снизить действующие давления и уменьшить, тем самым, энергозатраты на прессование и износ матрицы.

Плотность компактов зависит не только от действующего давления, но и от времени выдержки компакта под давлением. Необходимая рабочая площадь матрицы, определяющая необходимое время выдержки, определится по формуле:

F=k Qt vs kпLρср , где Q — производительность матрицы пресса; ρср — средняя плотность материала, находящегося в канале, kνs= 1,5–2,5 — коэффициент неравномерности распределения материала по поверхности матрицы, t — время пребывания материала в канале матрицы.

Исследованиями установлено, что оптимальной является двухвальцовая схема пресса [10], что определяет отношение радиуса вальца r к радиусу матрицы R . С учетом конструктивных соображений отношение r/R принимается равным 0,40–0,48.

Практикой установлено, что толщина катка вальца, необходимая для обеспечения достаточной жесткости, должна быть равной t k =λ 1 r , где λ 1 = 0,25–0,35.

Зависимость ширины вальца B от его радиуса r запишется в виде:

^   B / r>2 ( 1 — X 1 )( 2 + X a ) X п ,                                        (8)

где     для     подшипников     средней     широкой     серии     значение     λп = 0,33–0,38,

λ а = 0,24–0,28.

С учетом значения r/R может быть определен радиус матрицы пресса:

_R= F                                          (9)

I r I

2 пп | — I I R )

После определения R, используя ранее выбранные значения ψ и r/R, определяются радиус и ширина вальца:

r = ( r / R ) R,B = V r

Максимальную частоту вращения матрицы пресса можно определить по формуле:

n max

<—

2π

[a]

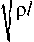
R

4k п

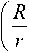
— 1 + R + L + —

)          2

где [σ] — допустимая прочность гранул на разрыв, Па; l — длина гранул.

Суммарная сила прессования, действующая на рабочие органы пресса, определится по формуле:

P=P₁cos α ₁+P₂cos α ₂+P₃cos α ₃

где P 1 — равнодействующая давлений, действующих в зоне уплотнения; P 2 — равнодействующая давлений в зоне проталкивания; P 3 — равнодействующая давлений в зоне упругого расширения материала; а 1 — угловая координата наклона равнодействующей давления уплотнения; а ₂ — угловая координата равнодействующей давлений проталкивания; а ₃ — угловая координата равнодействующей давлений в зоне упругого расширения.

Мощность N , необходимая для осуществления рабочего процесса пресса, определится по формуле:

N = 2nnz ( R — r )( P₁sin a ₁ +P₂ sin а ₂ — P 3 sin a 3 ) ,                              (13)

где z — число вальцов, n — частота вращения матрицы.

Далее определяется мощность двигателя, используемого для привода пресса:

N ge = 1,25N / n                                          (14)

где η — коэффициент полезного действия трансмиссии пресса, множитель 1,25 — коэффициент запаса мощности двигателя пресса.

Обсуждение и заключения. Предлагаемая методика позволяет определять основные параметры пресса с кольцевыми матрицами исходя из предъявляемых к компактам требований, структурно-механических свойств уплотняемого материала и рекомендуется для проектирования машин, обеспечивающих формирование биомассы в компакты с заданными свойствами.