Процесс распространения сейсмической волны, воздействующей на подземное сооружение
Автор: Бутунов Ж.Р., Хамидов С.
Журнал: Экономика и социум @ekonomika-socium
Рубрика: Основной раздел
Статья в выпуске: 6-1 (97), 2022 года.
Бесплатный доступ
Рассмотрено воздействие сейсмической волны на подземное сооружение. Поднятые вопросы решаются в аналитических специальных функциях. Получены и проанализированы численные результаты.
Сооружения, сейсмическая волна, функции бесселя и ханкеля, продольная волна, сдвиговая волна
Короткий адрес: https://sciup.org/140298922
IDR: 140298922
Текст научной статьи Процесс распространения сейсмической волны, воздействующей на подземное сооружение
Введение. При землетрясения от очага к сооруженного подходит сейсмическая волна, которая несет с собой определенную энергию. Если эпицентр близкой, а гипоцентр глубокий по отношение к рассматриваемому сооружению первой к нему подходит объемная продольная волна, т.е. волна сжатия -растяжение. Она проходит по сооружению так же, как в грунт, меняя при этом свои характеристики из - за изменения упругих свойств среды. За объемной продольной подходит объемная поперечная(сдвиговая) волна, которая и несет с собой основную массу энергии.
Постановка задачи и методики решения .
В случая достаточна протяженной подземных сооружений и воздействия, направленного перпендикулярного ее продольной оси, окружающая среда и обделок сводится к плоской задаче динамической теории упругости (или вязко упругости). В предположении обобщенного плоско деформированного состояния уравнение движения в смешениях имеет вид [1]
д2и
(Л + 2g)gr addivu — grotrot и + b = р —, (1)
где Л ид -модули упругости, называемыми постоянными Ламе; b -вектор плотности объемных сил (b = 0); р-плотность материала, UI - вектор смешения, который зависит от r,0,t. Поставленная задача решается в потенциалах перемещений
U = uri + u g k ;
дф 1 ду 1 дф ду и =--+---; Un =----
∂r r ∂θ r ∂θ ∂r
Потенциалы ф и у удовлетворяют волновому уравнению
X д 2 Ф
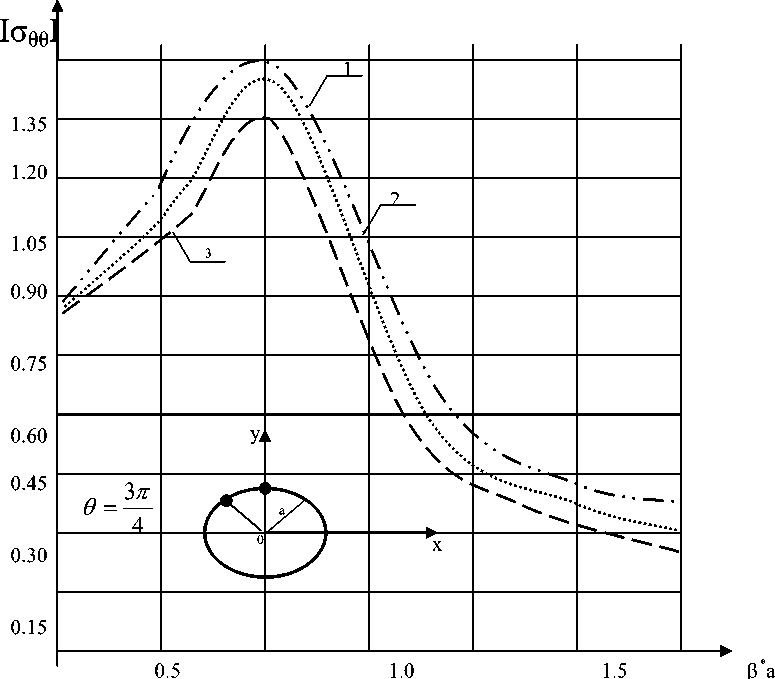
СО, ; V 2у = 1 д 2у Св atr где ф и у -является потенциалы перемещений, Са и Ср -фазовая скорость распространения волн расширения и сдвига. В работе[1] показано, что жидкость можно считать идеальной, а ее движение безвыхревым и изотермическим. При давлениях до 100 МПа движение жидкости в полнее удовлетворительно описывается волновыми равнениями для потенциалов скорости частиц жидкости [2] ∇ϕ= 1 д2ф Cf dtf ’ где Со- скорость звука в жидкости. Потенциал φ и вектор скорости жидкости связаны зависимостью V = gradp. Давление жидкости можно определить с ∂ϕ Р = роС0 ^ , где Ро- помощью линеаризованного интеграла Коши-Лагранжа плотность жидкости. При условии безотрывного обтекания жидкости нормальная компонента скорости жидкости и оболочка на поверхности их контакта должны быть равны. Отсюда следует следующие граничное условия ∂ϕ ∂ur ∂n Sо ∂t где Sо- поверхность контакта;n-нормальные поверхности оболочки; ur-перемещения оболочки по нормали. Падающая плоская волна расширения (или сдвига) рассматривается распространяющейся в положительном направлении оси х и представляется следующим образом т (Р) _ т ifi (ах - at) (р) (р) _ i(fix—at) (р) где ϕ0 или ψ0 –величина амплитуды:ω- круговая частота 2 2 / /^2 а = a / Cp и в2= а2/ Св -волновые числа расширения и сдвига соответственно. Если граница области, в которой изучается волновое поле, уходит в бесконечность, тогда требуются дополнительные условия в бесконечности. В первые эти условия получены Зоммерфельдом и подробно обсуждены в работах [1,2]. Если функции ϕ удовлетворяет уравнению Гельмгольца (в нашего случая удовлетворяет), то однозначность решения задачи в бесконечной области можно обеспечить требованиям условия излучения Зоммерфельда. Здесь r радиус в цилиндрической системе координат. На границе двух тел, выполняется условие жестокого контакта, т.е. выполняется условие равенства соответствующих перемещения и напряжения а(1)=а(2) • • и)1} =и(2)- и^ = и(2 rr rr ; rθ rθ ; r r ; r r . Одна из задач посвящена распространению гармонических сдвиговых волн, в двумерном упругом теле с круглым отверстием (подкрепленным). В такой постановке изучается наложение подходящих волн и отраженных от отверстия волн сдвига и растяжения–сжатия, что приводит к концентрации напряжения. Решение дифракционной задачи для плоской гармонической сдвиговой волны * получено в [1], которые имеет следующий вид (^ев = ^вв / п0; а0=цР2^0; ^0 - амплитуда падающих волн, ц - коэффициент Ламе) в П2~2> . n n2 — 1Hn (aa) _ * ^вв Где A n = aaHn —1(aa) (n2 — 1)0 aHn—1 (в a) — (n3 — n +| в" a2) Hn (0a ) + +Hn (aa ) —(n3 — n +10a 2)0aHn4( 0a) + (n2 — n — 10a0a2 Hn (0a) Hn(P, a) - функция Ханкеля; a = ro/Cp; P = ro/CS; Cp и CS - соответственно скорости распространение продольных и поперечных волн; го - круговая частота, п = 3,14. Расчеты методами теории упругости дают при отсутствии обделки вокруг отверстия и длине волны существенно больше диаметра отверстия следующее приближенное выражение для напряжений по периметру cS где G-модуль сдвига для грунта, и0-амплитуда скорости падающий сейсмические волны. Численные результаты и обсуждения. Ввиду того, длинно сейсмических волна как правило превышают характерные размеры поперечных сеченый выработок (например диаметр D), особой интерес представляют решение дифракционных задач для длинноволновых воздействий, т.е. D когда — < 1. Максимальные коэффициенты Л динамических концентраций напряжений Кσ (отношение максимальных напряжений на контуре к амплитуде падающей плоской волны) на рис.1, в зависимости от значений параметры и коэффициента Пуассона ν материала λ плоскости. При больших длинах волн ( = 0,04 ÷ 0,16) максимальные λ коэффициенты динамических концентраций оказалась на 5–10% больше, чем при соответствующие двуосном статическом нагружены (λ→∞)[1]. При D > 0,16 λ динамические концентрации напряжений существенно ниже статических. Числовые результаты, представленные на рис.1 и рис.2 , показывает, что здесь в отличие от случая жесткого включения [1], величина Кσ очень сильно зависит от D . Учет вязких свойств материала окружающей среды при расчета на действие λ сейсмических волн, снижает напряжения и перемещения на 10–15%. Расчеты показывает, что при фиксированных значениях амплитудах и длительности действия падающий волны с увеличениям акустических параметров жидкости, прогибы и усилия также увеличиваются. В области длинных волн распределения напряжения трубы с жидкостью и без жидкостью отличается до 15%, а в области коротких волн в некоторых значениях частоты они отличается до 40%. Анализ полученных результатов позволяют сделать следующие выводы. Методы волновой динамики позволили решить ряд плоских и пространственных задач о концентрациях напряжений в линейно упругой постановке. Полученные результаты показывают, что при воздействии сейсмических волн на сооружения возникает сложное поле, которое принципиально не может быть изучено другими методами. Рис.1 Зависимость коэффициента концентрации напряжения от длины волны. В следующим примере рассмотрим поле динамических напряжений и смешений, возникающее вблизи горных выработок (цилиндрических полости) и включения произвольной плотности в упругой среде при прохождении плоской волны сдвига. Падающая плоская волна сдвига рассматривается в положительном направлении оси х и представляется следующим образом ∞ ^p) = ^0 ^ eninJn (вг)cos n^ e-i^t, ^(p) = ° , n =0 где Vo - величина амплитуды; го - круговая частота; а в = го/Ср - волновое число сдвига; Ср =p/p; X и р - константы Ламе; р - плотность; sn = {1, n=0; 2, n>1}; Jn - функция Бесселя; v0 - амплитуда падающих волн; (г,0) - полярная системы координат. Граничные условия при г=а, где a - радиус цилиндрической поверхности разрыва будет агг=аг9=0 (радиальное и касательное напряжение). Коэффициенты An и Bn - определяются из предыдущих условий для каждого значения n. Рис.2 Изменение кольцевых напряжены в зависимость от волнового числа β а при воздействия поперечных волн в цилиндрическом теле. 1 – упругая среда (А=0). 2- А=0,01; в=0,05; v=0,25 ; а=0,1 3-А=0,05;в=0,01; v=0,25 ; α=0,1 На границе r=a безразмерные напряжения а*00(а00/а0, а0=рР2^0) выражаются следующими формулами _ * 8 ^вв =--I 1 п V 1 k2 то S n=1 n + 1 i г n n2 V — 1 ea i 2 7 A n Hn (aa) --sin ne где k2= в2/ a2= -a cP 2(1—v) 1 — 2v ; v - коэффициент Пуассона; An = P2a2I n2+ n — Hn—i(pa) + 1 n — n 3 — П 22 \ P aI ■j Hn (aa)Hn (Pa ) + aP a2(n 2 — 1)Hn t (aa) x [Pa Hn а)Hn—1 (Pa) + aa Hn-1 (aa)Hn (pa)]. Все выражения для напряжений и смешений имеют вид (R + i Im)e—'”t = (r2 + Im2 У2 e—i(M—Y). Пусть дана в безграничной деформируемой среде цилиндрическая полость. В этом случае единственным, не обращающимся в нуль, напряжением на границе является a00, поэтому оно одновременно и представляет, собой максимальное главное напряжение и смещение были получены для значений V = 0.25, А=0.01; P = 0.05; a = 0.1 .Результаты расчетов распределения ^^| при различных значениях волновых чисел приведена на рис. 2. Следует заметить ,что при P*а = 0,1 и распределения напряжений почти такое же ,как в статическом случая, P а = 1,5 в то времени как при боле высоких волновых числах распределение напряжений значительно отличается от статического случая Следует отметит, что максимальное напряжение достигается в 0 = 450 и 1350; а также распределение напряжение при 0а=0,099 почти такой же как в статическом случае, в то время как при более высоких волновых числах распределение напряжений значительно отличается от статического. Отношения плотностей п=р0/р1 оказывает большое влияние на напряжения, смещения и поворот жесткого включения. По мере возрастания плотности включения максимальные величины напряжения, смещения и поворот возрастают. 0а = 0,099 почти такой же как в статическом случае, в то время как при более высоких волновых числах распределение напряжений значительно отличается от статического. Отношения плотностей р=р0/р1 оказывает большое влияние на напряжения, смещения и поворот жесткого включения. По мере возрастания плотности включения максимальные величины напряжения, смещения и поворот возрастают. Таким образом, разработанная методика и алгоритм для решения поставленных задач, позволяют найти напряженно-деформированное состояние цилиндрических тел при воздействии гармонических волн.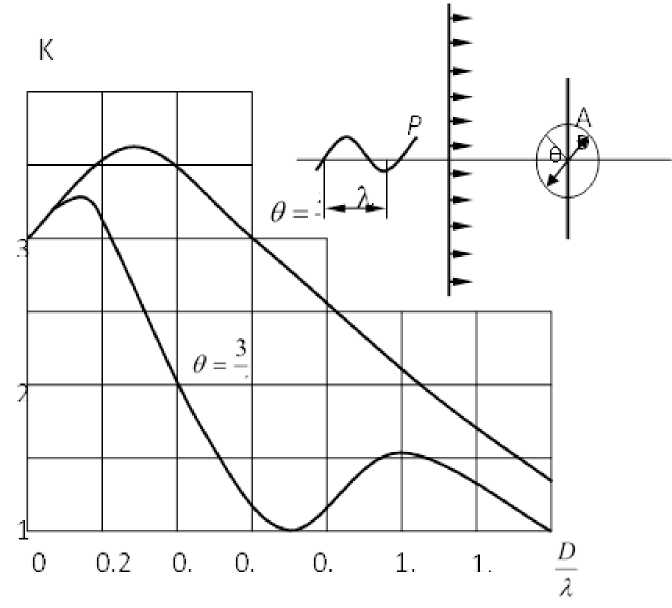
Список литературы Процесс распространения сейсмической волны, воздействующей на подземное сооружение
- Выборнов Б. И. Ультразвуковая дефектоскопия / Б. И. Выборнов. - М.: Ме-таллургия, 1985. - 256с.
- Ландау Л.Д. Теоретическая физика. В 10-ти т. Т.VII. Теория упругости: Учеб. пособие. / Л.Д. Ландау, Е.М. Лифшиц. - М.: Наука, 1987. - 248 с.
- Бутунов Ж.Р., Аблокулов Ш.З. КОЛЕБАНИЯ ВЯЗКОУПРУГИХ ЦИЛИН-ДРИЧЕСКИХ ОБОЛОЧЕК С ЖИДКОСТЬЮ // Universum: технические науки: электрон. научн. журн. 2022. 3(96). URL: https://7universum.com/ru/tech/archive/item/13303.


