Прочность и деформативность цементного камня и порошково-активированных бетонов. Часть II

Ерофеева И.В., Максимова И.Н., Светлов Д.А., Бакушев С.В., Шеин А.И., Тараканов О.В. Прочность и деформативность цементного камня и порошково-активированных бетонов. Часть II. Нанотехнологии в строительстве. 2025;17(6):647–665. – EDN: NUJVGH.

Introduction. Reinforced concrete structures in buildings and structures are subject to various loads during operation, which cause deformation and destruction. Materials and Methods. It has been shown that the strength and elastic-plastic properties of modern concretes can be broadly controlled using superplasticizers, nanoadditives, fillers, and fine aggregates. This article examines the deformation and fracture processes of cement paste and powder-activated concrete. The key characteristics of concrete deformation processes are determined using stress-strain diagrams, taking into account the downward strain curve. The concrete deformation diagram on the descending branch is fixed by the ultimate deformation, corresponding to the concrete reaching its maximum strength value, and the end point of the descending branch, corresponding to the residual strength of the concrete. Results. Complete concrete stress-strain diagrams with an extended descending section were obtained by loading specimens at a constant, decaying strain rate, resulting in a smooth decrease in stress in the specimen along the descending section. The influence of formulation factors on the key parametric points of the σ–ε diagram was studied. The influence of the W/C ratio, modifying additive, and polycarboxylate superplasticizer on the structure-forming factors for cement stone was examined. For concrete, the influence of the W/C ratio, modifying additive, polycarboxylate superplasticizer, fine filler, rheological filler, and reactive filler was examined. The resulting diagrams were analyzed for each material structure, both with an individual structure-forming factor and for powder-activated concrete as a whole. It was found that increasing the W/C ratio from 0.267 to 0.350 resulted in more elastic behavior of the material under load, a significant (4–5 times) elongation of the descending branch of the full equilibrium stressstrain diagram of hardened cement paste, and a change in the failure mechanism of the material. The specific parameters for static destruction of the sample are reduced by 12.1 times and the static J-integral Ji is reduced by 9.1 times.. It was shown that with the addition of the carboxylate superplasticizer "Melflux 1641F," the deformation pattern of the specimen under load was closer to that of cement paste obtained using normal-thickness cement paste, however, with a shorter (10 times) descending branch, indicating more brittle behavior of the specimen. The use of finely dispersed quartz also affected the nature of the deformation of the samples: their elasticity increased from 1.3 to 1.7 times, but at the same time the magnitude of ultimate deformations decreased by 20%, that is, the samples became more elastic and less deformable. Conclusion. It has been established that, with optimal component contents of cement stone and powder-activated concrete, crack resistance parameters significantly increase by 1.3 to 5.8 times, especially the static J-integral Ji, which characterizes the ductile fracture energy of the material at the crack tip, increasing due to the increased adhesion of the cement stone to the active surface of the microsilica. The curves of the complete equilibrium diagrams are approximated in sections by simple linear and quadratic functions or represented by a cubic polynomial.

ACKNOWLEDGEMENTS: This study is supported by a 2025 grant for fundamental scientific research (R&D) by research teams at National Research Moscow State University of Civil Engineering, project №. 05-661/130.

The research was conducted using the facilities of the Main Regional Center for Collective Use of Scientific Equipment and Facilities at National Research Moscow State University of Civil Engineering with the support of the Ministry of Science and Higher Education of the Russian Federation (agreement №. 075-15-2025-549).

СТРОИТЕЛЬНОЕ МАТЕРИАЛОВЕДЕНИЕ

Бетонные элементы и железобетонные конструкции в зданиях и сооружениях во время эксплуатации подвержены воздействию различных нагрузок, которые вызывают деформации и разрушения. Показано, что прочностные и упруго-пластические свойства, долговечность современных бетонов в широких пределах регулируются с помощью суперпластификаторов, нанодобавок, наполнителей и мелких заполнителей [1–6]. Применение реактивно-порошковых бетонов способствует получению бетонов с улучшенными физико-механическими свойствами и эксплуатационными характеристиками [7–11].

Реактивно-порошковый бетон (RPC) – это новый вид конструкционного материала с высокой прочностью, высоким модулем упругости и долговечностью. В данных бетонах отсутствует крупный заполнитель. В этой связи они формируются без границы раздела переходных областей между частицами, что придает им более высокую устойчивость к растрескиванию [7, 4, 12, 13]. Доказана перспективность применения реактивно-порошковых бетонов в сталебетонных композитных балках, позволивших при замене обычного бетона повысить трещиностойкость, жесткость и долговечность балок [8, 14]. Сконструированная Т-образная балка из реактивно-порошкового бетона малой высоты показала высокую предельную несущую способность с высокими результатами коэффициента безопасности (более 2,2) [9, 10].

Российские и зарубежные исследователи работают над оптимизацией составов порошковых бетонов на макро-, микро-, нано- и пикомасштабных уровнях [15–18]. К настоящему времени разработаны составы реактивно-порошковых бетонов на основе фундаментальных положений физикохимии водно-дисперсных систем, преимущественно микрометрических и в меньшей степени нанометрических водных суспензий и их реологии [16, 18]. Авторами получены микрометрические суспензии цемента и порошков из горных пород и их перевод в высококонцентрированные и агрегатно устойчивые при минимальном количестве воды [19–22].

Перспективными являются нанотехнологии получения бетонов с применением добавок гидросиликатов [23]. Прогресс в области ускорения твердения цементных систем гидросиликатными зародышами кристаллизации поднялся на высокий уровень. В настоящее время как за рубежом, так и в России синте- зированы нанометрические гидросиликаты кальция (с супертонкими частицами) в суспензионном виде [23–25].

Данная статья посвящена исследованию дефор-мативности цементного камня и реактивно-порошковых бетонов. Известно, что основные характеристики процессов деформирования и разрушения материалов устанавливаются с помощью диаграмм «напряжение–деформация» ( σ–ε ). Для этого в инженерных расчетах могут быть использованы различные виды диаграмм [26–29]: криволинейные, характеризующие поведение бетона, в том числе с ниспадающей ветвью; кусочно-линейные (двух-, трехлинейные). Диаграммы криволинейного типа характеризуют зависимость между напряжениями и деформациями в виде криволинейной линии. Эти диаграммы используются для описания поведения материала при пластических деформациях. Показана эффективность применения данного метода при нагружении материалов растягивающими усилиями. Характерными точками на таких диаграммах выделяют соответствующие пределы текучести (напряжение, при котором деформации растут без заметного увеличения нагрузки) и пределы прочности (напряжение, при котором материал разрушается). Кусочно-линейные диаграммы, к которым относятся двухлинейные и трехлинейные, аппроксимируются гладкой нелинейной зависимостью между напряжением и деформацией. Такая замена гладкой нелинейной зависимости кусочно-линейным приближением значительно упрощает решение статических задач. Эти методы применяются при описании деформационного поведения микроразрушенных, пористых и волокнистых материалов с упругими, вязкими и пластическими свойствами. В частности, двухлинейные диаграммы, представляющие собой зависимость между напряжениями и деформациями в виде прямых участков, также применяют для описания напряженно-деформированного состояния сжатого бетона или растянутой арматуры. В этом случае нормальные напряжения на участках упругих деформаций изменяются по закону Гука пропорционально относительным деформациям, а на участках пластических деформаций остаются постоянными. Применение трехлинейных диаграмм эффективно в тех случаях, когда требуется определить связь между напряжениями и относительными деформациями

СТРОИТЕЛЬНОЕ МАТЕРИАЛОВЕДЕНИЕ с учетом нагрузки различной продолжительности действия. Такого рода трехлинейные диаграммы используются для расчета деформаций железобетонных элементов при оценке напряженно-деформированного состояния в сжатом и растянутом бетоне по нелинейной деформационной модели при отсутствии трещин. Данный метод позволяет уточнить высоту сжатой зоны сечения и достичь экономии арматуры по сравнению с традиционным расчетом с прямоугольной эпюрой напряжений в бетоне.

Общий вид и основные параметрические точки диаграммы деформирования σ–ε бетона при сжатии приведены на рис. 1.

На диаграмме σ–ε выделяются три области развития деформации: линейная – на восходящей ветви – характеризует упругие деформации (сопровождается уплотнением бетона); упруго-пластическая – нелинейный участок восходящей ветви – характеризует необратимые пластические деформации (сопровождается разуплотнением бетона); пластическая стадия – нисходящая ветвь деформирования – характеризует пластические деформации, ведущие к разрушению бетона. То есть полные деформации бетона складываются из упругих (линейных) и длительных (являющихся как обратимыми, подчиняющимися принципу суперпозиции, так и необратимыми, нелинейно зависящими от напряжений) [30–32].

Существуют разные интерпретации кривой деформирования. В.М. Бондаренко изначально исходит из положения Р. Ольсона, что с точки зрения молекулярно-кинетической теории строения твердых тел существует только нелинейная связь между напряжениями и деформациями, а линейная связь (в виде общеизвестного закона Гука) является лишь упрощенной записью уравнения состояния мате- риала, допустимой только при весьма малых напряжениях [33–35]. В его работах деформации бетона предлагается складывать из мгновенных (неупру-гих-нелинейных) и запаздывающих нелинейных. Поэтому он предлагает свой вариант инженерного расчета железобетонных конструкций с использованием интегрального модуля деформаций.

Полученные разными авторами диаграммы свидетельствуют о том, что с ростом скорости деформации максимальное напряжение увеличивается, а также растут соответствующие предельные деформации (по линейному закону), а время до начала разрушения снижается по степенному закону [36–41].

Неоднородность структуры бетона вызывает разные относительные деформации на разных базах измерения. Предельные деформации при этом зависят от размера образцов, режима загружения (предельные деформации малых образцов больше). Диаграммы более неоднородных материалов сильнее искривлены. Для достоверности суждения о качестве материалов установлены стандарты на размеры образцов и правила проведения испытаний.

К прямолинейному участку относится модуль упругости (модуль Юнга). В случае отсутствия такого участка модуль упругости находится по касательной к кривой. При длительном действии нагрузки деформации могут увеличиваться во времени, то есть бетону присущи деформации ползучести. При медленном загружении, благодаря ползучести бетона, напряжение частично релаксирует – происходит перераспределение напряжения и изменение вторичного поля напряжения. Ползучесть особенно интенсивно развивается с повышением напряжения и пластичности бетона и уже заметно проявляется при сравнительно небольшом времени нагружения.

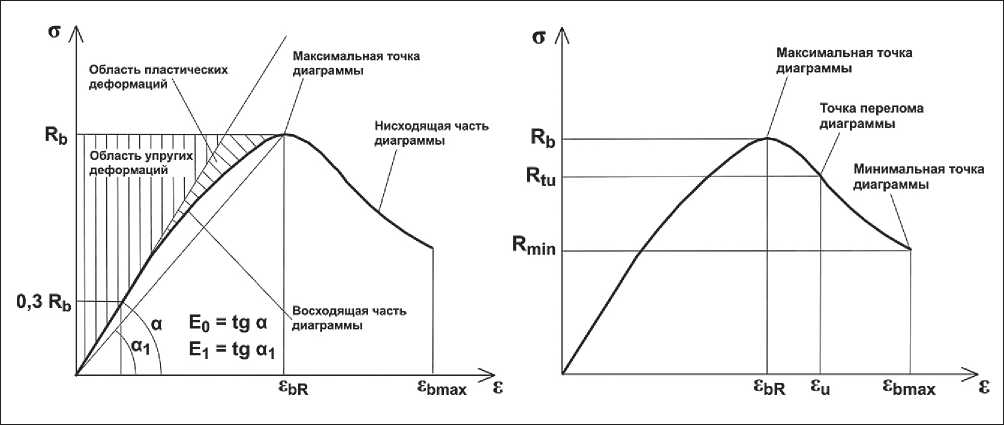
Рис. 1. Диаграмма напряжения-деформации для бетонов [29]

СТРОИТЕЛЬНОЕ МАТЕРИАЛОВЕДЕНИЕ

При высокой скорости нагружения жидкая фаза практически не успевает попасть в устья вновь образующихся микротрещин и повлиять на дальнейшее их развитие. Это можно отследить при времени нагружения до времени разрушения меньше 0,2–0,3 с.

Разрушение бетона происходит постепенно. Вначале возникают перенапряжения, а потом трещины в отдельных микрообъемах, распределение напряжений и вовлечение в трещинообразование большего объема материала, вплоть до образования сплошного разрыва того или иного вида, который зависит от формы образца (конструкции), ее размеров и других факторов. На последней стадии нагружения процесс микроразрушений становится неустойчивым и носит лавинный характер.

Разрушение бетона при сжатии обусловлено развитием микротрещин отрыва, направленных параллельно действующему усилию. Происходит кажущееся увеличение объема образца. Процесс развития микротрещин определяется структурой бетона, а также видом и режимом приложенной нагрузки. Надо отметить, что процесс развития микроразрушений на диаграммах поведения бетона « σ_С–ε_С » обнаруживается только с помощью сопоставления продольных и поперечных деформаций бетонного образца. Повышение трещиностойкости для бетонных элементов и железобетонных конструкций является важнейшей задачей. Особенно это важно для материалов и изделий, используемых для строительства высотных зданий и сооружений [42], большеразмерных бетонных балок [43], изделий, подвергаемых ударным нагрузкам [44], элементам, подвергающимся растягивающимся нагрузкам [45, 46], для свайных фундаментов [47], соединений балок с колоннами [48], предварительно напряженных балок [49], для мостовых конструкций [50].

Актуальными являются исследования, направленные на установление аналитических выражений, максимально отражающих физическую нелинейность поведения бетонов при нагружении [51]. В этом случае физическая линейность в большей степени связывается с трещинами и их развитием. Деформативные свойства бетона с учетом нисходящей ветви деформации изучали во многих работах [52, 53].

Предельная деформативность бетона зависит от различных факторов. Диаграмма деформирования бетона на нисходящей ветви фиксируется следующими параметрическими точками: εbR (предельная деформативность бетона соответствует достижению бетоном максимального значения прочности Rb), εbu, εbmax (конечная точка ниспадающей ветви диаграммы соответствует остаточной прочности бетона Rmin). Диаграммой оцениваются различные состояния бетона как до образования трещин, так и после их возникновения. В настоящее время деформатив-ные свойства порошково-активированных бетонов, в зависимости от основных структурообразующих факторов, изучены недостаточно.

ЦЕЛЬ И ЗАДАЧИ ИССЛЕДОВАНИЯ

Целью исследования является изучение процессов деформирования и разрушения цементного камня и порошково-активированных бетонов.

Задачи исследования:

• 1.    Составить аналитический обзор работ отечественных и зарубежных авторов в области исследования деформативности цементного камня и бетонов на основе диаграмм «напряжение-деформация».

• 2.    Обосновать для проведения исследований составы цементных матриц бетонов нового поколения: 1) цемент, молотый наполнитель, пластификатор, вода (матрица первого рода); 2) цемент, молотый наполнитель, тонкий наполнитель фракции 0,1–0,5 или 0,16–0,63 мм, пластификатор, вода (матрица второго рода); 3) матрица первого рода или матрица второго рода, включающая мелкий заполнитель фракции 1,0–5,0 или 0,63–5,0 мм (матрица третьего рода).

• 3.    Определить влияние ключевых структурообразующих факторов цементного камня и порошковоактивированных бетонов на основные параметры трещиностойкости: статический джей-интеграл; удельные энергетические затраты на разрушение; статический коэффициент интенсивности напряжения.

• 4.    Получить диаграммы «напряжение-деформация» для цементного камня и порошково-активированных бетонов и описать влияние основных рецептурных факторов на основные параметрические точки. При этом в качестве типа исследуемых диаграмм выбрать диаграммы с нисходящей ветвью, которые позволяют изучать наряду с упругими упруго-пластические и пластические свойства.

• 5.    Исследовать влияние ключевых структурообразующих факторов на основные физико-механические свойства цементного камня и порошковоактивированных бетонов.

• 6.    При исследовании цементного камня в качестве структурообразующих факторов следует рассматривать влияние В/Ц-отношения, модифицирующей добавки и суперпластификатора, а при изучении порошково-активированных бетонов наряду с вышеуказанными – тонкодисперсного наполнителя, реологического и реакционного наполнителей. Выполнить анализ полученных диаграмм для материалов как с отдельным структурообразующим фактором, так и для порошково-активированного бетона в целом.

• 7.    Провести аппроксимацию полных равновесных диаграмм.

• 8.    Предложить полиномиальные зависимости «напряжение–деформация» с целыми нечетными показателями.

• 9.    Записать дифференциальные уравнения для характерных случаев деформирования бетона.

СТРОИТЕЛЬНОЕ МАТЕРИАЛОВЕДЕНИЕ

МАТЕРИАЛЫ И МЕТОДЫ

Основным вяжущим служил бездобавочный цемент производства ООО «Ульяновск-цемент». Характеристики свойств, химический и минералогический состав используемого цемента приведен в табл. 1 и 2.

В качестве пластифицирующей добавки использовался гиперпластификатор (ГП) серии «Melflux» – «Melflux 1641F» на основе поликарбоксилатных эфиров (производитель – компания Degussa Constraction Polymers, SKW Trostberg, Германия), по строению – это привитые сополимеры. Отличаются тем, что диспергирование (дефлокуляция, разрушение агломератов, пластификация) происходит по электросте-рическому принципу.

Характеристики гиперсуперпластификатора приведены в табл. 1.

В качестве реологически активного дисперсного наполнителя использовалась каменная мука, а в качестве каменной муки использовали микрокварц ЛГОК (Липецкий горно-обогатительный комбинат). Характеристики микрокварца представлены в табл. 2.

В качестве реакционно-химической пуццолано-вой добавки применяли микрокремнезем, характеристики которого представлены в табл. 3.

В качестве тонкозернистых наполнителей и песка-заполнителя использовали пески Смольненского карьера Ичалковского района Республики Мордовия и Храмцовского карьера Ивановской области. Физико-химические характеристики наполнителей и зерновой состав песков приведены в табл. 4–7.

Для исследований были выбраны составы, приведенные в табл. 8.

Образцы на основе цементных паст готовили вручную. Перед приготовлением смесей компоненты взвешивали. Взвешивание цемента и суперпластификатора осуществлялось на электронных весах с точностью до 0,01 г. При приготовлении смесей вначале готовился раствор сухого суперпластификатора в воде. Далее этот раствор добавлялся в цемент.

Таблица 1. Характеристики гиперсуперпластификатора «Melflux 1641F»

Характеристики	Melflux 1641F
Внешний вид, цвет	Порошок, цвет от желтоватого до коричневого
Потери при высушивании, % по массе	max 2,0
Насыпная плотность, кг/м3	400–600
Реакция – pH 20% раствора t = 20 °C	6,5–8,5
Рекомендуемая дозировка по отношению к массе связующего, %	0,05–1,0

Таблица 2. Характеристики микрокварца

Песок липецкий (формовочный)
Размеры сит, мм	Остатки на ситах, г	Частные остатки, %	Полные остатки, %	Модуль крупности
5	0	0	0
2,5	0	0	0
1,25	0	0	0
0,63	5	0,25	0,25
0,315	205	10,25	10,5
0,16	1620	81,0	91,5	1,02
менее 0,16	155	7,75	102

Таблица 3. Характеристики липецкого микрокремнезема

Наименование материалов	Содержание SiO2, %		Цвет	ρист, кг/м3	ρнас, кг/м3	Sуд, м2/кг
	всего	в том числе аморфного
Порошкообразный липецкий МК-65	70	60–65	Темносерый	2,3	178	6000

СТРОИТЕЛЬНОЕ МАТЕРИАЛОВЕДЕНИЕ

Таблица 4. Характеристики песка Ичалковского карьера Республики Мордовия

№ п/п	Свойство	Ед. изм.	Показатель
1	Класс песка	–	1
2	Модуль крупности	–	1,7
3	Объемно-насыпная масса	г/см3	1,35
4	Содержание пылеватых и глинистых частиц	%	2,0
5	Содержание глины в комках	%	0,2
6	Коэффициент фильтрации	м/сут	3

Таблица 5. Характеристики песка Храмцовского карьера Ивановской области

№ п/п	Наименование показателей	Требования ГОСТ 8736–2014	Фактические показатели
1	Модуль крупности	2,5–3,0	2,76
2	Содержание пылеватых и глинистых частиц, %	Не более 2,0	1,0
3	Содержание глины в комках, %	Не более 0,25	Отсутствует
4	Насыпная плотность, кг/м3		1 580
5	Содержание вредных компонентов и примесей: SO3, % аморфные разновидности SiO2, ммоль/л	0–1,0 0–50	0,37 28,83
6	Удельная эффективная активность естественных радионуклидов песка, Бк/кг	До 370–1-й кл.	39

Таблица 6. Характеристика зернового состава кварцевого песка Ичалковского карьера Республики Мордовия

Остатки	Остатки на ситах, %, с размером отверстий, мм
	2,5	1,25	0,63	0,315	0,16	поддон
Частные	0,28	1,11	6,44	32,16	47,34	12,67
Полные	0,28	1,39	7,83	39,99	87,33	100

Таблица 7. Характеристика зернового состава кварцевого песка Храмцовского карьера Ивановской области

Остатки	Остатки на ситах, %, с размером отверстий, мм
	2,5	1,25	0,63	0,315	0,16	поддон
Частные	9,63	8,89	34,35	35,37	9,94	1,82
Полные	9,63	18,52	52,87	88,24	98,18	100

Таблица 8. Составы композиций для изготовления образцов

Компоненты	Содержание компонентов, мас. ч, для состава
	1	2	3	4	5	6
Цемент ульяновский ПЦ 500 Д0	1	1	1	1	1	1
Вода	0,267	0,35	0,171	0,6	0,475	0,525
ГП «Melflux 1641F»	–	–	0,009	0,009	0,009	0,009
Микрокремнезем липецкий	–	–	–	–	0,1	–
Микрокварц	–	–	–	1,1	0,75	–
Кварцевый песок фракции 0–0,63 мм	–	–	–	2,753	1,775	2,065
Кварцевый песок фракции 0,63–2,5 мм	–	–	–	2,347	1,975	1,76

СТРОИТЕЛЬНОЕ МАТЕРИАЛОВЕДЕНИЕ

В составах с суперпластификатором количество воды принималось таким, чтобы обеспечивалось получение теста нормальной густоты.

Бетонные смеси готовили с помощью миксера или бетоносмесителя гравитационного действия. Сыпучие исходные материалы бетонной смеси, а именно отдозированные по массе портландцемент, наполнители и заполнители, последовательно вводились в бетоносмеситель с водой затворения и пластификатором, смесь тщательно перемешивалась до получения самоуплотняющейся однородной массы, заливалась в стандартные формы и уплотнялась на лабораторной виброплощадке. Образцы изготавливались размерами 4×4×16 см в металлических формах, которые предварительно смазывали парафином. Твердение образцов проходило при термовлажностной обработке, после того как в течение одних суток они твердели в формах в ванной с гидравлическим затвором.

Для получения равновесной диаграммы «усилие – перемещение» (« F – V ») при испытаниях образцов повышенной хрупкости (высокопрочных) на трещиностойкость была использована установка повышенной жесткости. На основании данных усилия F и перемещения V строилась диаграмма « F – V », показанная на рис. 2.

Далее экспериментальную диаграмму трансформировали в расчетную по требованиям ГОСТ 29167. С этой целью, пользуясь средствами графического редактора AutoCAD, по набору данных восстанав-

ливали диаграмму деформирования. Алгоритм выполняемых операций приводится ниже.

Алгоритм выполняемых операций при определении трещиностойкости был принят следующим: – с начала прямолинейного нисходящего участка диаграммы, то есть из точки D, где выполняется условие (dF/dV) ~ const, проводили отрезок DK, перпендикулярный оси OV;

– из точки С опускали перпендикуляр СН к оси ОV и линию СА , параллельную упругой линии ОТ ;

– определяли величину отрезка OM из выражения:

v^ = v>---------ГЧ—2----

1 + 2,8<р ² +6<р'1( _г —^) '(5,58

1 + 2,8^ 2

- 19.57Z + 36,82^ 2

, (1)

-34,94^ 3 + 12,77V)I

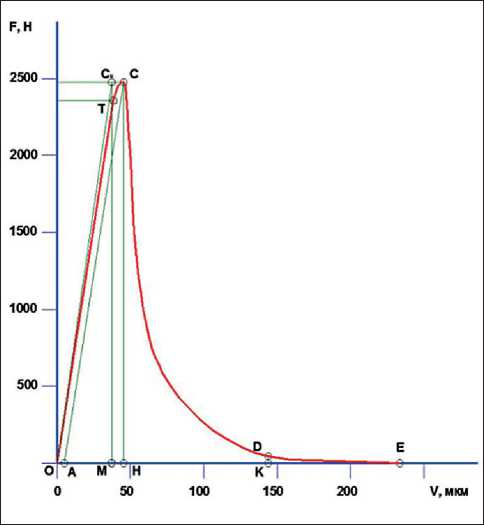
Рис. 2. Равновесная диаграмма деформирования образца № Т17 [51]

где λ = а ₀ /b ; φ = b/L ₀; V_e – упругие перемещения образца (отрезок АН на рис. 2);

– из точки М восстанавливали перпендикуляр МС_и ^с к оси ОV до пересечения с линией СС_и ^с , параллельной оси ОV . Точку О соединяли с точкой С_и ^с отрезком ОС_и ^с .

Использование равновесной диаграммы позволяет определять энергетические и силовые характеристики испытуемого материала.

Пользуясь средствами AutoCAD, определяли площади на равновесной диаграмме, которые соответствуют энергозатратам ( W , МДж), связанным с: W_m – процессами развития и слияния микротрещин до формирования магистральной трещины статического разрушения (равны площади ОТСА на рис. 2); W_е – упругим деформированием до начала движения магистральной трещины статического разрушения (равны площади АСН на рис. 2); W_i – локальным статическим деформированием в зоне магистральной трещины (равны площади НСDК на рис. 2).

Вычисляя площадь треугольника ОС_и ^с М , определяли расчетные энергозатраты на упругое деформирование сплошного образца:

Mi = F _mM ;/2 ,

где F_m – максимальное значение усилия, достигнутое в ходе испытаний.

Значения удельных энергозатрат G , MДж/м² вычисляли по соответствующим формулам.

G_i – удельные энергозатраты на статическое разрушение до момента начала движения магистральной трещины:

p    ^Mm^+Me

¹      t(b-a o ) ^,

где t = b – геометрические размеры поперечного сечения образца; а ₀ – длина начальной трещины.

G_F – удельные эффективные энергозатраты на статическое разрушение:

СТРОИТЕЛЬНОЕ МАТЕРИАЛОВЕДЕНИЕ r _ W,-We ^             .

^r     t(b-a o )

_E = ^

^b V ^c 4 b ^4.

G_СЕ – полные удельные упругие энергозатраты на статическое деформирование образцов до разделения его на части:

GCe =

Wce

t(b-a o )

Влияние технологических факторов на трещино-стойкость бетона оценивается в двух областях работы образца – до момента страгивания магистральной

После страгивания трещины и вплоть до разделения образца на две части критериями трещино-стойкости являются: W_i – энергозатраты, равные площади НСДК на рис. 2; G_F – удельные энергозатраты, вычисляемые по формуле (4); K_с – критический коэффициент интенсивности напряжений, МПа·м^1/2, вычисляемый по формуле

KC = V GCEEb .

трещины и после ее страгивания вплоть до разделения образца на две части.

До момента страгивания магистральной трещины критериями трещиностойкости служат: W_m – энергозатраты, МДж, равные площади ОТСА на рис. 6; W_i – энергозатраты, МДж, равные площади НСДК на рис. 2; G_i – удельные энергозатраты, вычисляемые по формуле (3), а также статический джей-интеграл, МДж/м², вычисляемый по формуле

По результатам испытаний формируются итоговые табл. 9, 10, 11.

ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ И ИХ АНАЛИЗ

J = Wm + We - Wui i b(b — ao)

.

К_i – статический коэффициент интенсивности напряжений, МПа·м^1/2:

K, = 7G,- Eb,

где статический модуль упругости бетона E_b , МПа, вычисляется по формуле

В данном разделе представлены результаты исследования прочности, трещиностойкости и характера деформирования образцов цементного камня и порошково-активированных бетонов и аппроксимация полных равновесных диаграмм.

Равновесные испытания образцов осуществляли по ГОСТ 29167–91 с оценкой влияния структурообразующих факторов на энергетические и силовые параметры трещиностойкости. Результаты испытаний приведены в табл. 12 и 13.

Из результатов испытаний, приведенных в табл. 12, следует, что повышение водоцементного отношения обусловливает резкое снижение, в пер-

Таблица 9. Определение характеристик трещиностойкости образца № Т17. Исходные данные

Состав образца	Режимы отверждения	Геометрические размеры образца					Масса образца, кг	Плотность образца, кг/м3	Влажность (весовая), %
		L·103	B·103	H·103	A0·103	L0·103
Т17	ТВО	160	40	40	4	120	0,581	2270	3,0

Примечание: L – длина образца; B – ширина; H – высота; A0 – длина наведенной в образце трещины; L0 – расстояние между опорами образца.

Таблица 10. Значения нагрузки F , H, величины перемещений V , м в характерных точках на кривой « F–V »

C		H		T		A		D		M		E
Fc·103	Vc·103	F H ·103	V H ·103	FT·103	VT·103	F A ·103	V A ·103	FD·103	VD·103	F M ·103	V M ·103	FE·103	VE·103
2503,0	32,0	0,0	32,0	2385	18,8	0,0	11,8	22	219	0,0	18,2	0,0	278,0

Таблица 11. Расчетные характеристики материала

Energy characteristics							Crack resistance		Properties of concrete
W e , Дж	W m , Дж	W i , Дж	W ui , Дж	G i , Дж	G F , Дж	J i , Дж	K i , МПа-м 1/2	R tbf , MПa	E , MПa	X cF , м	R , MПa pp ,	R , MПa
1	2	3	4	5	6	7	8	9	10	11	12	13
0.0248	0.029 39	0.193381	0.022797	37.44375	151.5008	21.61228	0.931784	6.436214	23187.38	0.084802	6.8	10.5

СТРОИТЕЛЬНОЕ МАТЕРИАЛОВЕДЕНИЕ

Таблица 12. Влияние гиперпластификатора «Melflux 1641F» на параметры трещиностойкости цементного камня

Номер состава	G F		J i		K i
	Дж/м2	отн. ед.	Дж	отн. ед.	MПa·м1/2	отн. ед.
1	558,3	1,00	34,2	1,00	1,60	1,00
2	46,3	12,1	3,76	9,1	1,12	1,43
3	150,6	3,71 0,31	42,19	0,81 0,09	1,15	1,39 0,97

Таблица 13. Влияние тонкодисперсного кварца на параметры трещиностойкости песчаного бетона

Номер состава В/Ц GF J i K i Дж/м2 отн. ед. Дж отн. ед. MPa·m1/2 отн. ед. 4 0,6 127,0 2,1 25,8 3,3 0,63 1,3 5 0,475 149,4 2,5 45,5 5,8 1,27 2,6 6 0,525 60,1 1,00 7,9 1,00 0,49 1,00 вую очередь, энергетических параметров механики разрушения – уменьшение в 12,1 раза удельных энергозатрат на статическое разрушение образца GF и в 9,1 раза – статического джей-интеграла Ji, при этом силовой критерий, оцениваемый величиной статического коэффициента интенсивности напряжений при нормальном разрыве, снизился лишь в 1,4 раза, т.е. на величину, сопоставимую со снижением прочностных показателей (см. табл. 12).

Как следует из данных табл. 13, вызванное применением суперпластификатора резкое уменьшение водоцементного отношения привело к снижению в 3,71 раза удельных энергозатрат на статическое разрушение образца по сравнению с образцом № 1 и к их росту в 3,25 раза по сравнению с образцом № 2 с высоким водосодержанием. При этом наблюдается рост статического джей-интеграла J_i , характеризующего нелинейность процессов деформирования материала у вершины трещины, – незначительное (на 23%) по сравнению с образцом на цементном тесте нормальной густоты (состав № 1) и существенное (в 11,22 раза) – при высоком водоцементном отношении (состав № 2). Силовой критерий, оцениваемый величиной статического коэффициента интенсивности напряжений при нормальном разрыве K_i , по аналогии с критерием G_F , имеет максимальное значение на цементе нормальной густоты, т.е. как повышение, так и понижение В/Ц приводят к снижению важнейших параметров трещиностойкости материала.

В табл. 13 приведены данные сравнительных испытаний по определению параметров трещино-стойкости порошково-активированного бетона. Как следует из их результатов, применение тонкодисперсного кварца существенно – от 1,3 до 5,8 раза – повышает параметры трещиностойкости исследуемого бетона, особенно статический джей-интеграл

J_i , характеризующий энергию вязкого (пластического) разрушения материала у вершины трещины, возрастающую вследствие повышения сцепления цементного камня с активной поверхностью микрокремнезема. С другой стороны, эффект введения тонкодисперсного кварца мог бы оказаться еще более выражен, если бы не различное водоцементное отношение составов, при том, что, как было установлено выше, влияние водоцементного фактора на параметры трещиностойкости не только существенно, но может быть и неоднозначным – как снижение, так и повышение В/Ц относительно некоторого рационального его значения приводит к снижению трещиностойкости цементного камня.

Введение тонкодисперсного кварца в виде микрокварца (молотого песка) и микрокремнезема (аморфная форма с удельной поверхностью 50 000 см2/г) оказало существенное влияние на прочность песчаного бетона при изгибе (табл. 13): добавка микрокварца (состав № 4) привела к увеличению прочности в 1,7 раза, а совместно микрокварца и микрокремнезема (состав № 5) – в два раза.

На рис. 3, 4 приводятся полные равновесные диаграммы составов, указанных в табл. 8, на одноосное сжатие.

Водоцементное отношение оказало влияние также на характер деформирования образца под нагрузкой (рис. 3). При пониженном его показателе наблюдается более крутой восходящий участок на равновесной диаграмме деформирования (см. рис. 3а), что характеризует более упругое поведение образца и повышенный модуль упругости по сравнению с цементным камнем при пониженном В/Ц (см. рис. 3б); но при этом наблюдается и более продолжительная ниспадающая ветвь до полного разрушения (разделения на две половинки) образца-балочки.

СТРОИТЕЛЬНОЕ МАТЕРИАЛОВЕДЕНИЕ

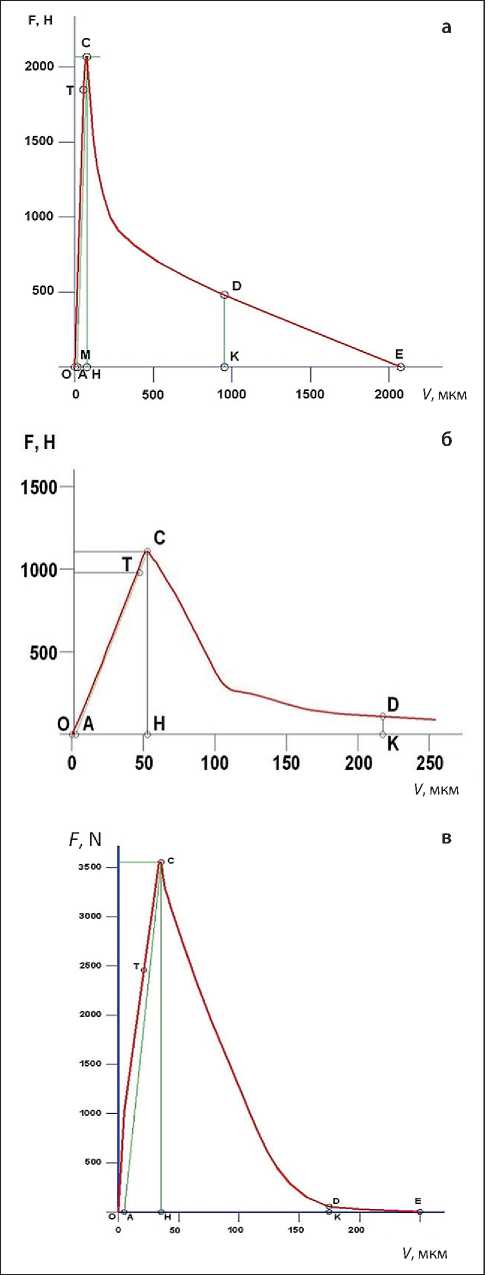
Рис. 3. Полная равновесная диаграмма деформирования цементного камня составов: а – № 1; б – № 2; в – № 3

При применении гиперпластификатора характер деформирования образца состава № 3 под нагрузкой ближе к цементному камню состава № 1 (см. рис. 3а) с расходом воды, соответствующим нормальной густоте цементного теста, однако с более короткой (в 10 раз) ниспадающей ветвью, что говорит о хрупком характере разрушения образца (рис. 3в).

Использование тонкодисперсного кварца повлияло и на характер деформирования образцов (рис. 4) – повысилась их упругость от 1,3 до 1,7 раза, но при этом на 20% снизилась величина предельных деформаций, т.е. образцы песчаного бетона становятся более упругими и менее деформативными, что согласуется с общими представлениями о повышении хрупкости цементных образцов с повышением их прочности.

Анализируя результаты испытаний на сжатие в осях «напряжение-деформация», можно сделать вывод о том, что у всех исследуемых составов на начальном участке нагружения рост напряжения и деформации происходит по закону, близкому к линейному, но при дальнейшей деформации линейность нарушается, а при достижении предельных значений напряжения бетон интенсивно разрушается, что сопровождается снижением напряжения и ростом деформаций.

Для каждого состава на полученных диаграммах были выделены характерные точки с максимально достигнутыми напряжениями, после которых начинались разрушения образцов. Для этих точек определены соответствующие величины предельных деформаций ( ε_max ); зафиксированы также переходы от первого участка ко второму и от второго к третьему – для отдельных составов.

Проведем аппроксимацию полных равновесных диаграмм деформирования (рис. 5).

В соответствии с рис. 7, 8 кривые полных равновесных диаграмм следует аппроксимировать простейшими функциями – линейными и квадратичными – по участкам.

В работах [52–54] кривые объемного и сдвигового деформирования геометрически и физически нелинейной и линейной сплошной среды аппроксимированы билинейными [52] и биквадратичными [54] функциями. Эта аппроксимация позволила записать дифференциальные уравнения равновесия в перемещениях для характерных случаев деформирования сплошной геометрически и физически нелинейной и линейной сплошной среды: одноосного плоского деформирования, осесимметричного деформирования, центрально-симметричного деформирования, плоской деформации в декартовых и цилиндрических координатах.

Выделим основные параметрические точки на кривых полных равновесных диаграмм деформирования бетонных образцов (рис. 5):

СТРОИТЕЛЬНОЕ МАТЕРИАЛОВЕДЕНИЕ

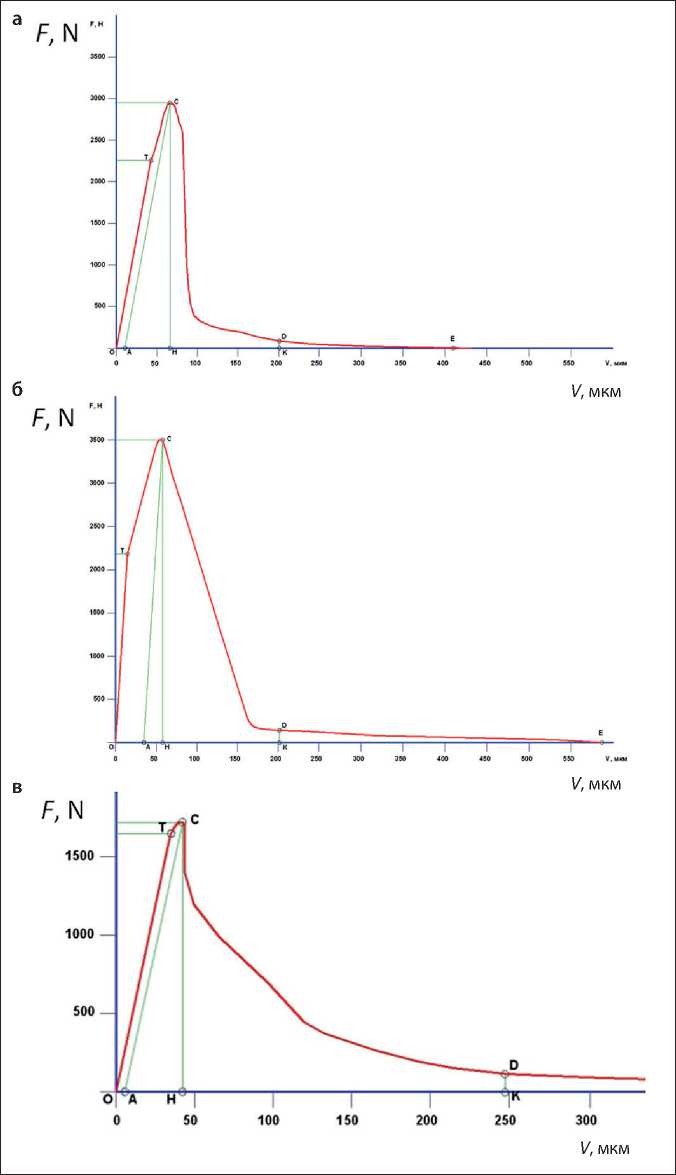
Рис. 4. Полные равновесные диаграммы деформирования песчаного бетона составов: а – № 4; б – № 5; в – № 6

Точка O. – Начальная точка диаграммы. σ ₀ = 0; ε ₀ = 0.

Точка T. – Конечная точка начального прямолинейного участка. σ_T ; ε_T .

Точка C. – Максиальное напряжение. σ_С ; ε_С .

Точка F. – Закрывает кривую, аппроксимирующую вершину. σ_F ; ε_F .

Точка D. – Точка изменения кривизны диаграммы. σ_D ; ε_D .

Точка Е. – Конечная точка нисходящей ветви диаграммы. σ_E ; ε_E .

Введем следующие аппроксимирующие функции:

Первый участок O–T, аппроксимируется линейной функцией: ax + b = y.

СТРОИТЕЛЬНОЕ МАТЕРИАЛОВЕДЕНИЕ

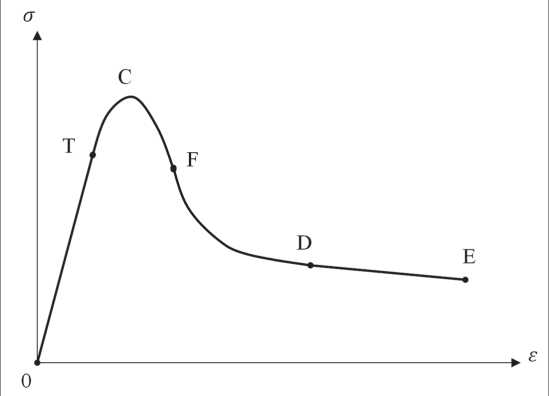
Рис. 5. Полная равновесная диаграмма деформирования

] Аэ Aq

Тогда ;         ;

д’ д’ д

В итоге:

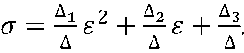
На втором участке ветви параболы направлены вниз, то есть кривизна параболы отрицательна:

й2<7    „     „

—г = 2с = 2

de1

^т ^т i

с ^с 1

(Тр s_F 1

^Т £т 1

£с £с 1

Ер Ер 1

.

Второй участок T–C–F, аппроксимируется параболой: cx ² + dx + e = y.

Третий участок F–D, аппроксимируется параболой: fx ² + kx + l = y.

Четвертый участок D–E, аппроксимируется линейной функцией: mx + n = y.

Определяем коэффициенты аппроксимирующих функций на основании основных параметрических точек на кривых полных равновесных диаграммах деформирования бетонных образцов.

Первый участок: ax + b = y

σ = aε + b,

0 = a· 0 +b, то есть b = 0 .

σ_T = a·ε_T, то есть a = σ_T/ε_T.

В итоге:

^т с = —г.

£т

Второй участок: cx ² + dx + e = y

σ = cε ² + dε + e ,

σ_T = cε_T ² + dε_T + e ;

σ_C = cε_C ² + dε_C + e ;

σ_F = cε_F ² + dε_F + e.

Решая данную систему линейных алгебраических уравнений, получаем:

Это возможно, если у числителя и знаменателя разные знаки.

Третий участок: fx ² + kx + l = y

σ = fε ² + kε + l ,

σ_F = fε_F ² + kε_F + l ;

σ_D = fε_D ² + kε_D + l ;

2 cε_F + d = 2 fε_F + k .

Решая данную систему уравнений, получаем:

k = 2 cε_F + d – 2 fε_F .

Тогда σ_F = fε_F ² + (2 cε_F + d – 2 fε_F ) ε_F + l ;

σ_D = fε_D ² + (2 cε_F + d – 2 fε_F ) ε_D + l .

Перепишем полученную систему:

σ_F = fε_F ² + (2 cε_F + d ) ε_F – 2 fε_F ² + l =

= – fε_F ² + l + (2 cε_F + d ) ε_F ;

σ_D = fε_D ² + (2 cε_F + d ) ε_D – 2 fε_D ² + l =

= – fε_D ² + l + (2 cε_F + d ) ε_D .

Вычитая из первого второе, получим:

σ_F – σ_D = – fε_F ² + fε_D ² + (2 cε_F + d )( ε_F – ε_D ).

То есть f - <^JF-^)-(2c_£F+d)(_£f-_£p)

То есть                               .

£d~£f

Складывая первое и второе, получим:

σ_F + σ_D = – fε_F ² – fε_D ² + 2 l + (2 cε_F + d )( ε_F + ε_D ).

То есть l = 1/2 [(σF + σD) + (fεF2 + fεD2) –

– (2 cε_F + d )( ε_F + ε_D )] = 1/2 [( σ_F + σ_D ) +

+ f ( ε_F ² + ε_D ²) – (2 cε_F + d )( ε_F + ε_D )].

Окончательно,

д=

с-2

£с

£f

£т £с £f

;

;

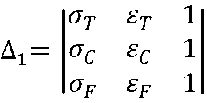
^£т ^£С ^£f

Ер (Jp £С °C Ер (Jp

(VF-VD)-(2CEF + d)(EF-£D\

f2-p2

;

△ 2=

с2

£т

£2

£с

£f

(Jp °C °F

;

к = 2csf + d — 2sf

(aF-ffD^-^CEp-Fd^Ep-ED).

;

£d £f

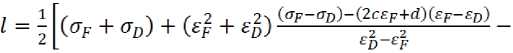
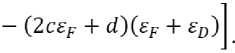
СТРОИТЕЛЬНОЕ МАТЕРИАЛОВЕДЕНИЕ

В итоге:

(o~f ~ ^d) ~ (2^££_f + dXe_F ~ ^£d) ₂

2      2

£d~£f

,    , j n Of “ °d) - (2ce_f + d)(e_F - £d)

ZC8p + Cl — ZEp --------------о----о-------------

.                         £d~£f           .

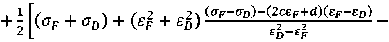
На третьем участке кривизна параболы положительна, то есть

(Fa

^=2/^2 й£^л

Of - °d) - (2c£F + d^Ep - £D)

2      2

£d - £f

Здесь знаменатель положителен. Тогда должно выполняться соотношение:

( σ_F – σ_D ) – (2 cε_F + d )( ε_F – ε_D ) > 0.

Или ( σ_F – σ_D )/( ε_F – ε_D ) > 2 cε_F + d .

Четвертый участок: mx + n = y

σ = mε + n .

σ_D = mε_D + n ; σ_E = mε_E + n .

Решая данную систему, получаем: σ_D – σ_E = m ( ε_D – ε_E ), то есть m = ( σ_D – σ_E )/( ε_D – ε_E ). σ_D + σ_E = m ( ε_D + ε_E ) + 2 n ,

то есть n

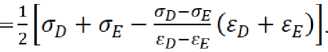
В итоге:

^ _£n — _£p £ + 2 [^ + £n—Sp ^^ "+" £^] . (13) ^£D~^£E L ^£D~^£E J

Итак, полная равновесная диаграмма аппроксимируется двумя прямыми и двумя параболами. В точке T и точке D аппроксимируемой кривой возможен излом; в точках C и F кривая непрерывна вплоть до производных второго порядка.

В табл. 14 представлены соответствия коэффициентов аппроксимирующих полиномов для полных равновесных диаграмм деформирования цементного камня составов, приведенных в табл. 8 и 9 (состав № Т17).

Удобно также пользоваться упрощенным вариантом оцифровки диаграмм.

Среднестатистическая кривая зависимости σ–ε бетона при кратковременном нагружении с постоянной скоростью имеет вид, приведенный на рис. 6.

При этом на диаграмме обнаруживается нисходящий участок. При выборе и построении аппроксимирующих зависимостей воспользуемся понятиями предельной сжимаемости [ε–] и предельной растяжимости бетона [ε+], т.е. деформациями бетона в момент разрушения. Для расчета при так называемом кратковременном нагружении можно принять предельную сжимаемость [ε–] ≈ 2,0·10–3, предельную растяжимость при осевом растяжении [ε+] ≈ (1,5÷3)·10–4), при изгибе и внецентренном сжатии [ε–] ≈ 3,5·10–3. Предельная растяжимость при изгибе существенно выше и краевые удлинения в этом

Таблица 14. Соответствия коэффициентов аппроксимирующих полиномов

	Первый участок O-T: σ 0 ; ε 0 ~ σ T ; ε T	Второй участок T-C-F: σ T ; ε T ~ σ F ; ε F	Третий участок F-D: σ F ; ε F ~ σ D ; ε D	Четвёртый участок D-E: σ D ; ε D ~ σ E ; ε E
Состав № 3 (рис. 3) Вид аппроксимирующей функции:	Линейная	Парабола. Точка F принимается ниже т.С на точке излома кривой СD	Парабола	Линейная. ^E = 0
Составы № 4, № 5, № 6. (рис. 4) Вид аппроксимирующей функции:	Линейная	Парабола. Точка F принимается ниже т.С в первой точке излома кривой СD	Парабола	Линейная. ^E * 0
Составы № Т17. (рис. 2) Вид аппроксимирующей функции:	Линейная	Парабола. Точка F принимается на уровне т.Т	Парабола	Линейная. Off = o
Составы № Т17. (рис. 2) Вид аппроксимирующей функции:	Линейная	Парабола. Точка F принимается ниже т.С в первой точке излома кривой СD	Парабола	Линейная. ^E * 0

СТРОИТЕЛЬНОЕ МАТЕРИАЛОВЕДЕНИЕ

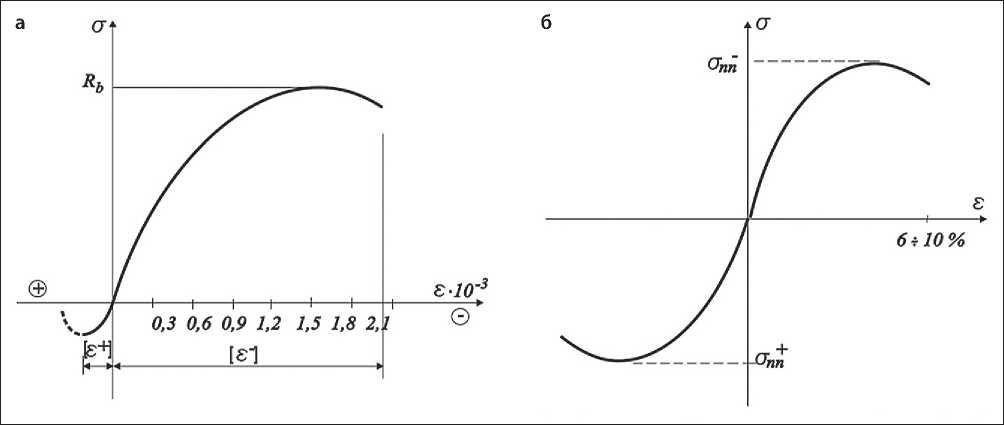
Рис. 6. Диаграмма деформаций бетона [55]: R_b = σ_nn – предел временного сопротивления материала бетона при сжатии

случае могут вдвое превышать ранее указанные значения.

При записи уравнений равновесия удобнее пользоваться зависимостями вида

Таким образом, при реализации поведения материала с учетом пластических деформаций сжатия и с учетом растяжения можно использовать соотношение (16).

σ = f ( ε ).

(14) ЗАКЛЮЧЕНИЕ

В достаточно общем виде такую зависимость можно записать следующим образом [56]:

^E^V^

А_г ■ E^ + A₂ ■ E^k2 + A₃ ‘ E^³ + ••• + A_n ■ E^kn, (15)

где A_i – некоторые физические константы, имеющие размерность напряжений; k_i – безразмерные показатели, которые могут быть любым положительным числом (целым, дробным).

Подбирая соответствующие значения A_i , k_i и число членов n , можно с необходимой точностью аппроксимировать любую экспериментальную диаграмму.

Если при деформации конструкции возникают напряжения разных знаков, то удобна аппроксимация зависимости σ–ε при помощи полинома с целыми нечетными показателями, например, кубическая зависимость [57]:

σ = E · ε – A ₃· ε ³,

обеспечивающая симметричность диаграммы относительно растяжения-сжатия.

Здесь E – начальный модуль упругости материала:

л ⁴ E³

A^ —     2 .

27 Onn

• 1.    Составлен обзор научно-технической литературы отечественных и зарубежных авторов в области исследования деформативности и расчета физикомеханических свойств материалов на основе диаграмм «напряжение-деформация».

• 2.    Установлены закономерности влияния рецептурных факторов (В/Ц-отношения, модифицирующей добавки, суперпластификатора, тонкодисперсного наполнителя, реологического и реакционного наполнителей) на деформативность цементного камня и порошково-активированного бетона.

• 3.    Путем проведения физико-механических испытаний образцов цементного камня и порошково-активированных бетонов получены диаграммы «напряжение-деформация» с нисходящей ветвью, которые позволили изучить, наряду с упругими, упруго-пластические и пластические свойства.

• 4.    Выявлено, что повышение водоцементного отношения с 0,267 до 0,350 вызывает более упругое поведение материала под нагрузкой, значительное (в 4–5 раз) удлинение ниспадающей ветви полной равновесной диаграммы деформирования цементного камня и изменение механизма разрушения материала. Повышение водоцементного отношения обусловливает резкое снижение, в первую очередь, энергетических параметров механики разрушения – уменьшение в 12,1 раза удельных энергоза-

• СТРОИТЕЛЬНОЕ МАТЕРИАЛОВЕДЕНИЕ

• 5.    Применение суперпластификатора «Melflux 1641F» привело к значительному уменьшению водоцементного отношения – с 1,56 раза по сравнению с составом на основе теста нормальной густоты и в 2,04 раза – по сравнению с составом с повышенным водосодержанием. При применении суперпластификатора характер деформирования образца под нагрузкой ближе к цементному камню на тесте нормальной густоты, однако с более короткой (в 10 раз) ниспадающей ветвью, что говорит о более хрупком поведении образца.

• 6.    Применение суперпластификатора привело к снижению в 3,71 раза удельных энергозатрат на статическое разрушение образца по сравнению с образцом на основе теста нормальной густоты и к их росту в 3,25 раза по сравнению с образцом с высоким водосодержанием. При этом наблюдается рост статического джей-интеграла J_i , характеризующего нелинейность процессов деформирования материала у вершины трещины, – незначительное (на 23%) по сравнению с образцом на цементном тесте нормальной густоты и существенное (в 11,22 раза) –

• 7.    Использование тонкодисперсного кварца значительно повлияло на характер деформирования образцов – повысилась их упругость от 1,3 до 1,7 раза, но при этом на 20% снизилась величина предельных деформаций, т.е. образцы становятся более упругими и менее деформативными. Применение тонкодисперсного кварца существенно – от 1,3 до 5,8 раза повышает параметры трещиностойкости исследуемого бетона, особенно статический джей-интеграл J_i , характеризующий энергию вязкого (пластического) разрушения материала у вершины трещины, возрастающую вследствие повышения сцепления цементного камня с активной поверхностью микрокремнезема.

• 8.    Полные равновесные диаграммы деформирования цементных композитов аппроксимированы по участкам линейными и квадратичными функциями. Аппроксимация диаграмм позволила записать дифференциальные уравнения в перемещениях для характерных случаев деформирования сплошной геометрически и физически линейной и нелинейной сплошных сред.

трат на статическое разрушение образца G_F и в 9,1 раза – статического джей-интеграла J_i , при этом силовой критерий, оцениваемый величиной статического коэффициента интенсивности напряжений при нормальном разрыве, снизился лишь в 1,4 раза, т.е. на величину, сопоставимую со снижением прочностных показателей (см. табл. 12).

при высоком водоцементном отношении. Силовой критерий, оцениваемый величиной статического коэффициента интенсивности напряжений при нормальном разрыве K_i , по аналогии с критерием G_F , имеет максимальное значение на цементе нормальной густоты, т.е. как повышение, так и понижение В/Ц приводят к снижению важнейших параметров трещиностойкости материала.