Продольная когерентность оптического поля протяженного пространственно некогерентного источника

Пространственно-временная когерентность оптического поля определяется и частотным, и угловым спектрами поля [1-6]. Принято считать, что в продольном направлении – в направлении распространения поля – когерентные свойства оптического поля определяются частотным спектром G(ω) этого поля. Полагается, что ширина функции продольной когерентности Γ(∆z ) – длина продольной когерентности Lc равна длине временной когерентности lc, которая обратно пропорциональна ширине частотного спектра ∆ω , lc ≈ 2π c/∆ω , где c - скорость света. Это вполне справедливо для направленного пучка света – для оптического поля с относительно широким частотным спектром G(ω) и достаточно узким угловым спектром I (α) в той области пространства, где рассматривается когерентность поля (ω- частота колебаний поля, α - угол между оптической осью пучка света и произвольным лучом, приходящим от источника в рассматриваемую область пространства). Однако для оптического поля с широким угловым спектром и достаточно узким частотным спектром функция и, соответственно, длина продольной когерентности могут определяться уже не частотным, а угловым спектром этого поля [3,7-27]. Для длины продольной когерентности в этом случае может быть использована [3,7-10,14,18,26,27] оценка Lc ≈ρII ≈2λ0/θ2 , где θ - ширина углового спектра, λ0 - средняя длина волны. В [11-13,15-17] с помощью интерферометра Май-кельсона экспериментально показано, при каких условиях в сигнале интерферометра можно наблюдать преимущественное влияние на продольную когерентность или частотного, или углового спектров оптического поля пространственно некогерентного ис- точника в зависимости от ширины этих спектров. В [18-21] эффект продольной пространственной когерентности рассматривается в задачах низкокогерентной интерферометрии по аналогии с широко известными методами, основанными на использовании эффектов временной когерентности [23-25]. Эффекты продольной пространственной когерентности наблюдаются в методе формирования совпадающих изображений (ghost imaging) [26,27] при использовании частично когерентного излучения протяженных тепловых источников.

Очевидно, оптическое поле может иметь такую ширину частотного и такую ширину углового спектров, когда продольная когерентность этого поля и, соответственно, функция продольной когерентности Г(Δ z ) в сравнимой степени зависят от параметров этих спектров. Длина продольной когерентности L c в этом случае должна определяться одновременно и шириной частотного, и шириной углового спектров оптического поля, L_c ( ∆ω , θ ) . Такая зависимость продольной когерентности в форме или явного выражения для фун кции продольной когерентности Γ ( ∆ z ; ∆ω , θ ) , или длины когерентности L_c ( ∆ω , θ ) , насколько нам известно, отсутствует в литературе, несмотря на подробное теоретическое описание когерентных свойств оптических полей [1-6]. Нам не известны также интерференционные эксперименты, в которых наблюдалось бы проявление продольной когерентности, определяемой одновременно и частотным, и временным спектрами оптического поля.

В настоящей работе получены выражения для функции продольной когерентности Γ(∆z; ∆ω, θ) и для длины продольной когерентности Lc (∆ω, θ) в зависимости и от ширины Δω частотного, и от ширины θ углового спектров оптического поля. Эти выражения по- зволяют определять продольную когерентность поля в условиях, когда продольная когерентность в сравнимой степени зависит от ширины частотного G(го) и углового I(а) спектров оптического поля. Полученная теоретическая зависимость Lc (Аго, 0) проверена экспериментально с использованием сканирующего интерферометра Майкельсона продольного сдвига с частотно широкополосным протяженным пространственно некогерентным источником света.

1.    Изменение длины продольной когерентности поля в процессе его распространения

Ширина углового спектра оптического поля 0 протяженного пространственно некогерентного источника света (например, теплового) изменяется в широких пределах в пространстве распространения этого поля от источника до дальней области дифракции. В пространстве, примыкающем к источнику, поле имеет предельно широкий угловой спектр и для ширины этого спектра можно принять 0 = п/2. При удалении от источника ширина углового спектра в свободном пространстве уменьшается и становится пренебрежимо малой в дальней области дифракции. Следовательно, при относительно узком частотном спектре G(го) можно считать, что в пространстве вблизи источника длина продольной когерентности поля определяется шириной углового спектра, который оказывает преимущественное влияние на продольную когерентность, рц << lc, поэтому Lc = рц. Вдали от источника, вследствие уменьшения ширины углового спектра 0, там, где рц становит- ся существенно больше lc, рц >> lc, или, что эквивалентно, 0 << д/2 АХ/Х0 , длина продольной когерентности определяется уже шириной частотного спектра, Lc = lc, влияние которого в дальней области дифракции становится доминирующим.

В некоторой промежуточной области пространства должен иметь место переходный процесс, в котором проявляется приблизительно равное влияние и углового, и частотного спектров поля на его продольную длину когерентности L c . Равное и совместное влияние спектров можно расценивать как удвоенное влияние. Следовательно, ожидается, что длина продольной когерентности L c в этой области будет примерно в два раза меньше длины временной l c и длины пространственной р || когерентности, L c = l c /2 = рц/2.

С продольной когерентностью поля и, соответственно, с длиной продольной когерентности, связано представление о волновом цуге и его длине [1,2]. На рис.1 схематически представлено изменение длины продольной когерентности поля – длины волнового цуга, в процессе его распространения от пространственно некогерентного источника. В пространств е вблизи источника, где рц << lc, волновой цуг имеет длину р|| , определяемую шириной углового спектра 0 . В этой области волновой цуг в процессе своего распространения постоянно испытывает амплитудно-фазовые декорреляционные изменения, обусловленные влиянием некоррелированных различны х угловых компонент поля [12,13,15].

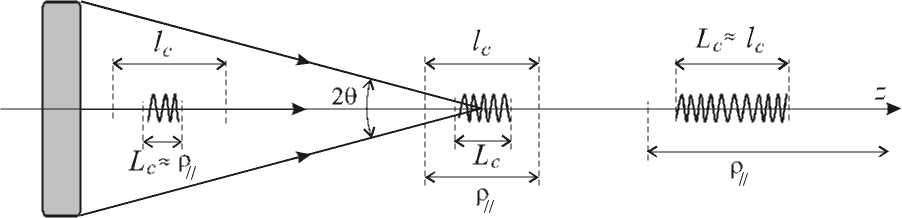
Рис.1. Изменение длины волнового цуга в поле излучения пространственно некогерентного источника

Используя оценочные формулы для длины временной когерентности l _c = Х ²₀ / АХ и для длины когерентности рц = 2 X 0,9 ² = 8 X 0 z ² [ D ² , где D - поперечный размер источника, z - расстояние от источника, можно приблизительно графически отобразить предполагаемое изменение длины продольной когерентности L _c ( z ) . Ниже мы получили формальное выражение для L _c ( z ) в зависимости от ширины частотного и углового спектров АХ и 0 и представили соответствующие графические зависимости.

2.    Функция и длина продольной когерентности

В свободном пространстве оптическое поле в большинстве случаев можно отнести к классу квази- однородных случайных полей [5] - случайных полей с достаточно медленно меняющимися в пространстве статистическими параметрами в сравнении с их корреляционной длиной и с достаточно медленным изменением в пространстве самой корреляционной длины. Для таких полей, как известно, возможно использование соотношения Винера-Хинчина для определения корреляционных функций этих полей [5]. Поэтому для определения в явном виде выражений для функции r(Az; Аго, 0) и затем для длины Lc (Аго, 0) продольной когерентности в зависимости от ширины частотного и углового спектров поля можно воспользоваться соотношением Винера-Хинчина для функции продольной одновременной (Аt = 0) когерентности оптического поля Г(Аz, Аt = 0):

r ( A z , A t = 0 ) = J W ( k z ) exp ( ik_z A z ) dk_z , (1) —^

где r ( A z , A t = 0 ) = ( E ( z , t ) E * ( z — A z , t )) , E ( z , t ) - возмущение, создаваемое полем на продольной оси z (рис.2), а угловые скобки означают усреднение во времени; A t - взаимная задержка возмущений; k_z -пространственная частота пространственных флуктуаций оптического поля в продольном направлении z ( k_z - проекция волнового вектора k = ( 2 n/X ) N светового поля на ось z (см. рис.3)); W ( k_z ) - спектр пространственных частот волнового поля.

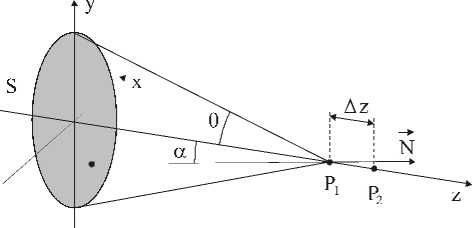
Рис.2. К определению функции продольной когерентности Г ( P 1 , P ₂, A t = 0 ) = r ( A z , A t = 0 ) оптического поля протяженного некогерентного источника S

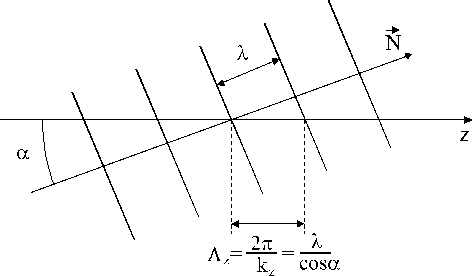
Рис.3. Пространственный период Л _z и пространственная частота k_z = 2л/Л _z вдоль продольной оси z некоторой угловой компоненты оптического поля

Пространств енная частота k_z зависит и от частоты to (от длины волны X ), и от угла а распространения плоской волны пространственного спектра поля относительно продольной оси z (рис.3)

2пto kz =—cos(а)=—cos(а).(2)

X

Поэтому ф ункция пространственного спектра W ( k z ) в уравнении (1) есть, фактически, пространственно-временной спектр поля, W ( k_z ) = W ( а , to ) . Следовательно, функция продольной когерентности r ( A z ) , важно подчеркнуть, определяется и угловым, и частотным спектрами оптического поля.

Рассмотрим протяженный пространственно некогерентный источник света. Предположим для простоты, что спектральная ф ункция поля такого источника W (kz ) = W (а, to) = W0 = const на всем диапазоне угловых направлений а и частот to. Иными словами, W(kz ) = W0 = const на всем диапазоне пространственных частот Akz = kzmax — kzmin, где k и k - соответственно, максимальное и zmax      zmin минимальное значения пространственных частот kz поля (рис.4):

kz max = ^it^^2 cos(а = 0) , c too — Ato 2

^k z min = ⁰--------^{cos (а}=e ) .                    ⁽³⁾

c to0 - центральная частота колебаний поля.

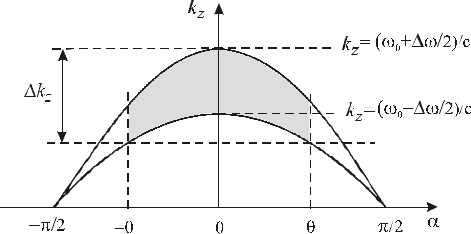
Рис.4. Диапазон изменения продольной пространственной частоты поля A k_z в зависимости от ширины частотного Ato и ширины углового 6 спектров поля

Тогда из (1) непосредственно след ует вполне ожидаемое оценочное соотношение для продольной длины когерентности

L _ 2п ^c ”A k z_z

.

Соотношение (4) также след ует и из явного выражения для r(Az), которое можно получить с использованием (1) при условии W(kz) = W0 = const во всем диапазоне пространственных частот Akz . Выполняя в (1) интегрирование, для ф ункции когерентности получаем след ующее выражение

^{r(A z} ) = ⁽ W ^ N k z ) sin^ k z ^A/^{2 )} expO k z 0 ^{A z} ) , ⁽⁵⁾ A k z A z / 2

где k_{z 0} - центральная пространственная частота,

V   (kz max + kz min )   kz0 =       2       =

2 n ( ₂6 1 AX . ₂6 / ’

= —I cos + sin I

X 0

2 2 X ₀     2

A k_z - диапазон пространственных частот поля (рис.4),

Nk = k „ —k- = z z max z min

= 2 п

f 2 . ₂6 AX ₂ — sin —+ —— cos (X 0 2 X ²0

6'

—

В (6) и (7) X0 и AX - центральная длина волны и ширина частотного спектра, выраженная в шкале длин волн, G(X).

При подстановке (6) и (7) в (5) имеем аналитическое выражение для функ ции продольной когерентности r ( A z ) в зависимости от ширины Аю или, соответственно, ширины АХ частотного спектра и от ширины 6 углового спектра поля.

Длину продольной когерентности Lc можно определить как расстояние Az, на котором модуль функции когерентности r(Az), определяемой (5), принимает первое нулевое значение. Для такой оценки получаем выражение, совпадающее с (4). Используя (7) и (4), для длины когерентности Lc получаем уравнение

L c

2 п

to. . 2 ( 0 I Ato 0 0-2- 2sin 1 — 1 +---cos — c I 2 J c 2

^2sin 2 ⁰ 2 ₊ А_2 ( 0 2 )

^А      л ₀

Полученное уравнение определяет зависимость продольной длины когерентности L_c и от ширины частотного спектра Аю (или АХ ), и от ширины углового спектра 6 оптического поля.

Анализ уравнения (8) показывает, что влияние на Lc сомножителя cos2 (б/2) во втором слагаемом ста- новится заметным только при широком частотном спектре, когда Аю = ю0 или АХ ~ Х0. В остальных случаях при малых углах 6 можно считать cos2 (б/2) ~ 1, а при средних и больших углах 6 имеет место преобладающее влияние на Lc первого слагаемого в (8) по сравнению со вторым слагаемым. Таким образом, сомножитель cos2 (б/2) во втором слагаемом (8) можно опустить и это уравнение записать в более наглядном и запоминающемся виде

” +Т , L c    ^р ||     l c

где l c =Х ₀ ² /аХ - длина продольной когерентности, определяемая шириной частотного спектра, которую принято называть длиной временной когерентности;

р=Х 0/ 2 sin ² ( 6/2 ) - (10) длина продольной когерентности, определяемая шириной углового спектра поля при достаточно узком частотном спектре поля.

Если l c >> р и , что эквивалентно Х ₀/ АХ >>  [ 2sin² ( 6/2 ) ]” , то, как следует из (9), L c = P I - длина когерентности определяется преимуществ енно угловым спектром поля. И наоборот, если l c << ри , то длина когерентности L_c определяется преимущественно частотным спектром поля, L c = l c . Оба этих предельных случая, как показано в [11-13,15], отчетливо наблюдаются в эксперименте с интерферометром Майкельсона.

В диапазоне сравнимых величин l c и р_н длина продольной когерентности L c определяется в сравнимой степени и угловым, и частотным спектрами оптического поля в соответствии с уравнением (9).

Уравнение (9) носит оценочный характер. Если определять полную длину когерентности L_c , например, по уровню 0,5 от максимального значения функции когерентности Г ( А ) , то аналогичным образом след ует определять и длины когерентности l_c и р н . Уравнение (9) в этом случае останется прежним. Если же контуры частотного и углового спектров имеют непрямоугольные и различные формы, то слагаемые в правой части уравнения (9) буд ут иметь некоторые неединичные сомножители, определяемые формами спектральных контуров.

На рис.5-7 представлены полученные с помощью уравнения (9) графические зависимости полной длины продольной когерентности L_c от 6 , АХ и от расстояния z от пространственно некогерентного источника света круглой формы. Зависимость L c ( z ) получена при использовании соотношения 6 ( z ) = arctg ( Dj 2 z ) , где D - диаметр источника. Там же, для сравнения, представлены графики для р нн ( 6 ) и р н ( z ), а также прямые для l c . Отметим, что при расчете l c и L c ( z ) мы не учитывали эффект дифракционного изменения ширины частотного спектра - эффект Вольфа и соответствующее изменени е длины временной когерентности этого поля [28-31].

Графики на рис.5-7 показывают заметное отличие полной длины L c от l c и от р ц в области сравнимых значений l c и р_н. Эти различия должны заметным образом проявляться в интерференционном эксперименте. График L c ( z ) на рис.7 показывает эволюцию длины продольной когерентности волнового поля в процессе его распространения от пространственно некогерентного источника (см. также рис.1). В области, непосредственно примыкающей к поверхности источника, где угловой спектр поля максимально широкий, длина продольной когерентности определяется шириной углового спектра. При удалении от источника возрастает влияние на продольную когерентность частотного спектра поля, которое становится доминирующим в дальней области дифракции.

Графики на рис.5-7 получены в предположении протяженного пространственно некогерентного источника с шириной спектрального контура Δλ=0,04мкм при средней длине волны λ0=0,63мкм. Для такого источника область наибольшего отличия полной длины когерентности Lc от длины временной когерентности lc и от длины рн лежит в диапазоне больших угловых апертур θ оптического поля, θ≈0,16÷0,6 рад (см. рис.5). В эксперименте нам пока не удалось сформировать для наблюдения эффектов интерференции оптические поля с такими широкими угловыми спектрами. Поэтому нам пришлось использовать дру- гой источник света с более узким частотным спектром и, соответственно, с большей длиной временной когерентности.

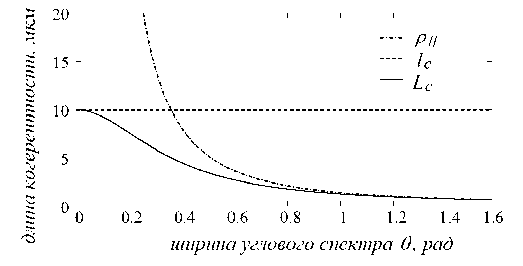
Рис.5. Длина продольной когерентности Lc в зависимости от ширины углового спектра 6 оптического поля при постоянной ширине ЛК = 0,04 мкм частотного спектра поля и К0 = 0,63мкм

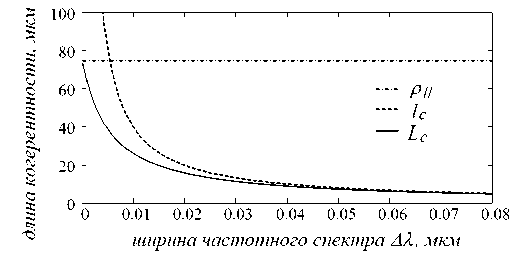
Рис.6. Длина продольной когерентности L c в зависимости от ширины AК частотного спектра поля при постоянной ширине 6 = 0,13 углового спектра этого поля и К ₀ = 0,63 мкм

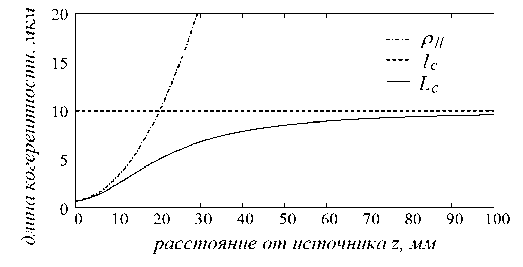
Рис.7. Длина продольной когерентности L c в зависимости от расстояния z от некогерентного источника диаметром D = 15 мм при постоянной ширине AК = 0,04 мкм частотного спектра поля и

К 0 = 0,63 мкм

3.    Определение длины продольной когерентности в интерференционном эксперименте

Проявление ограниченной продольной когерентности оптического поля в эксперименте можно наблюдать с помощью интерферометра Майкельсона с плоскими зеркалами без использования линз в плечах интерферометра (рис.8). Подробная методика такого эксперимента описана в [11-13,15].

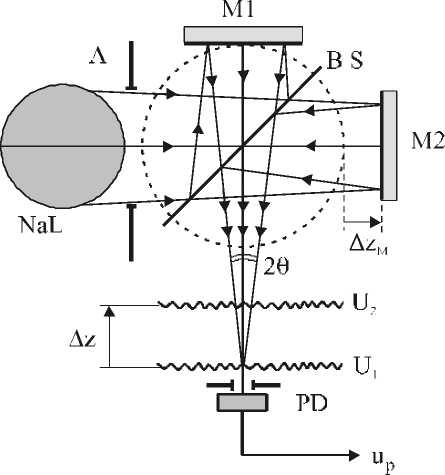
Ри с.8. Схема интерферометра Майкельсона для наблюдения эффектов продольной когерентности волнового поля с широкими угловым и частотным спектрами: NaL – натриевая лампа; A – апертурная диафрагма; BS – делитель пучка; M1 и M2 – плоские зеркала; U 1 и U 2 – идентичные волновые поля, отраженные зеркалами M1 и M2, соответственно; PD – фотодетектор; u_p – сигнал фотодетектора

При продольном смещении зеркала интерферометра на величину A z M на выходе интерферометра на оптической оси системы возникает взаимный продольный сдвиг A z = 2 A z M интерферирующих идентичных полей. При этом, как показано в [32], между этими волновыми полями отсутствует временная задержка, A t = 0 , которая рассматривается в функции пространственно-временной когерентности оптического поля r ( A z , A t ) , где A t никак не связано с A z и не определяется A z , A t Ф A z/c . Идентичные волновые поля, которые формируются в интерферометре путем деления по амплитуде исходного волнового поля, на выходе интерферометра накладываются друг на друга только с пространственным сдвигом. На оптической оси интерферо метра имеет место только продольный пространств енный сдвиг A z . Поэтому в интерференционном сигнале фотодетектора u_P , установленном на оптической оси интерферометра, проявляется фун кция продольной одновременной когерентности поля r ( A z , A t = 0 ) : u p ~ Re { r ( A z , A t = 0 )} . При непрерывном продольном сканировании зеркала интерферометра в сигнале фотодетектора u_P наблюдается интерференционный импульс продольной когерентности (см. рис.9), огибающая которого определяется Re { r ( A z )} . Ширина этого импульса в шкале разности хода волн в интерферометре A = 2 A z_M , которая равна взаимному продольному смещению волновых полей A z = 2 A z_M , определяется длиной продольной когерентности L_c .

Для экспериментальной проверки обсуждаемых в работе зависимостей полной длины когерентности Lc от ширины частотного и ширины углового спектров поля, Lc (∆ω, θ) , необходимо иметь в плоскости регистрации интерференционного сигнала на выходе интерферометра волновые поля с приблизительно одинаковыми длинами временной lc (определяемой частотным спектром) и продольной ρII (определяемой угловым спектром) когерентности. Именно в этом случае имеет место наибольшее отличие полной длины когерентности Lc от длины временной когерентности lc и от длины когерентности ρII . В наших экспериментальных условиях этим требованиям удовлетворял газоразрядный источник света -Na лампа низкого давления ДНАС18. Основная энергия излучения этого источника сосредоточена в области желтого дублета с длинами волн λ1 = 0,589 мкм и λ2 = 0,5896мкм. Модуль функции временной когерентности такого излучения, как это хорошо известно, имеет осциллирующий характер, что необходимо учесть при сопоставлении экспери- осциллирующий характер с полупериодом ∆Zc = 0,5λ1λ2 (λ1 -λ2) ≈ 289 мкм и огибающую с заметно большим интервалом спадания δzc ≈ λ1λ2 δλ ≈ 1800мкм при δλ ≈ 0,0002мкм.

Если пучок такого излучения имеет достаточно широкий угловой спектр, то возникает влияние этого спектра на продольную когерентность и, следовательно, на параметры огибающей интерференционного сигнала. Проявление этого влияния в эксперименте удобнее наблюдать по изменению ширины центрального импульса когерентности в интерференционном сигнале, когда длина когерентности ρ _|| , определяемая угловым спектром в соответствии с (10), имеет сравнимые значения с полупериодом осцилляций ∆ Z_c . В этом случае влияние ширины отдельных линий д ублета δλ можно уже не учитывать и для модуля ф ункции продольной когерентности, и, соответственно, для огибающей интерференционного сигнала вместо (14) можно записать приближенное выражение

Γ(∆z) ~ ментальных результатов с теоретическими данными.

Если считать, что отдельные линии желтого дуб-

~

лета имеют прямоугольную форму шириной δλ , то для функци и продольной когерентности с использо-

sin(2nAz sin2 (6/2)/%0)    ( % %, cos | П 1

( 2 nA z sin² ( 6/ 2 )/ % ₀ )       (   % 1 % ₂

. (15)

ванием (1) можно получить выражение

Γ ( ∆ z ) ~ ∆ k sin ⁽ 0,5 ^{∆ k 1 z ∆ z )} exp ( ik ∆ z ) + ^{1 z} ( 0,5 ∆ k 1 z ∆ z )          ^{1 z}

+ ∆ k 2 z

sin ( 0,5 ∆ k _{2 z} ∆ z ) ( 0,5 ∆ k _{2 z} ∆ z )

exp ( ik _{2 z} ∆ z )

где k _{1 z} , k _{2 z} и ∆ k _{1 z} , ∆ k _{2 z} определяются согласно выражениям (6) и (7) для λ ₁ и λ ₂ следующим образом

,     2п ( 2 (6I 1 8% . 2 6 I к . = — I cos I — I +---Sin — I ,

^{1 z} % 1 (     ( 2 J 2 % 1       2 J

2 π k 2 z ⁼

λ ₂

2 ( 61 1 8% . 2 6 I cos I   I +—-—sin — I;

2 J 2 % 2

^{2 п}I„ .2 ( ⁶Y ⁸%    :

A k,_ = —| 2sin — +-- cos ^{1 Z}   % 1 I 1 2 J % 1

2 91

’ 2J ,

^{2 n} U .2 ( ⁶1 . ⁸%   :

A к . = — I 2sin — +-- cos ^{2 Z} % 2 (      1 2 J % 2

2 θ

.

При узком угловом спектре ( θ ≈ 0) и при низком давлении в Na лампе, когда δλ<< λ ₁ - λ ₂ , для модуля ф ункции продольной когерентности (11) можно получить приближенное выражение

Γ(∆z)

sin ( n-8%-A zI % ² ₀ )    ( %,-%_{2 A} I ....

-p -------Y2Y cos | n 1 _л² A z I , (14)

( n-8%-A zI %q )     ( %1% ₂ J

где λ ₀ = ( λ ₁ +λ ₂ ) 2 . Это выражение показывает, что модуль функц ии продольной когерентности имеет

Это выражение позволяет легко увидеть конкурирующее влияние углового и частотного спектров на функцию и длину продольной когерентности и, соответственно, на огибающую интерференционного сигнала. Однако для количественного сопоставления экспериментальных и теоретических данных необходимо использовать более точное выражение (11) для функции Γ ( ∆ z ) , которое позволяет численно определить полную длину продольной когерентности L_c в зависимости от ширины углового спектра θ и от ширины частотного интервала ∆λ = λ ₂ - λ ₁ .

При экспериментальной оценке длины когерентности L_c по интерференционному сигналу удобнее определять полуширину интерференционного импульса когерентности на половине его высоты, поскольку экспериментальные импульсы имеют длинные «хвосты» из-за непрямоугольной формы реальных спектральных контуров излучения. В этом случае для длины когерентности излучения желтого дублета направленного пучка света ( θ ≈ 0) можем использовать следующую оценку L_c ≈ l_c ≈ 0,664 ⋅∆ Z_c ≈ 192 мкм. Соответственно и для ρ II вместо (10) надо использовать соотношение ρ _|| ≈ 0,6 ⋅ λ ₀ 2sin² ( θ 2 ) . Эти значения длин когерентности можно использовать для сопоставления экспериментальных и теоретических данных для L_c с использованием уравнения (9). Однако следует иметь в виду, что оценочное соотношение (9) получено при условии одинаковых по форме частотного и углового спектров. Для рассматриваемого случая с

дублетом имеем существенное различие форм этих спектров и, следовательно, в (9) должны использоваться некоторые поправочные коэффициенты.

На рис.9 представлены переменные составляющие интерференционных сигналов ~ P ( 2 A z M ) , наблюдаемые с использованием Na лампы низкого давления.

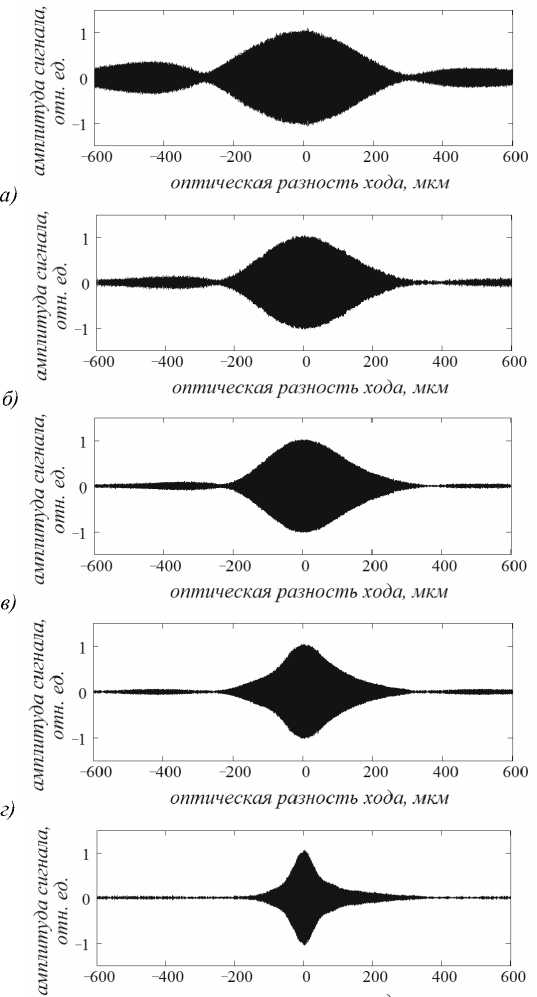
оптическая разность хода, мкм

д)

Рис.9. Нормированные переменные составляющие сигналов интерферометра Майкельсона с протяженным некогерентным источником (Na лампа) при различной ширине θ углового спектра интерферирующих световых полей: а – θ=0,04; б – θ=0,0475; в – θ=0,061; г – θ=0,065;

д – θ=0,105 рад

Сигналы записаны при различной ширине θ углового спектра интерферирующих полей (при различных размерах источника). Длина продольной когерентности Lc определялась как полуширина интерференционного импульса на половине его высоты. Экспериментальные значения Lc сопоставлялись с теоретическими значениями Lc, рассчитанными с использованием уравнения (11) при тех же значениях ширины углового спектра θ. Ширина углового спектра поля в плос- кости регистрации интерференционного сигнала определялась с помощью камеры обскура. Разность хода волн в интерферометре Δ и, соответственно, величина продольного сдвига Δz=Δ определялись по интерференционным осцилляциям в сигнале с использованием величины средней длины волны λ0≈(λ1+λ2)/2≈0,5893мкм. В представленных на рис.9 сигналах интерференционные осцилляции графически не разрешаются из-за их высокой частоты.

На рис.10 представлены экспериментальные значения длины когерентности L c в зависимости от ширины углового спектра 0 и теоретические кривые L _c ( 0 ) , полученные с использованием выражений (11) и (9).

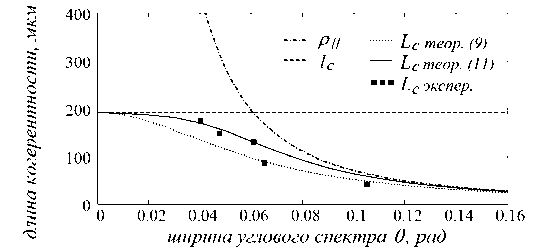
Рис.10. Экспериментальные значения длины когерентности L c в зависимости от ширины углового спектра 0 и теоретические графики L c ( 0 ) , р ц ( 0 ) и l c

Для сопоставления на рис.10 также представлена кривая 0,6 • р || ( 0 ) , полученная для 51 = 0 с использованием (10) при 1 0 ~ ( 1 1 + 1 2 )/ 2 = 0,5893мкм, и прямая L c ~ 192 мкм. Для ширины спектральных контуров желтого дублета 51 ~ 0,0002 мкм при расчетах мы использовали данные спектральных измерений, выполненных на спектрометре СДЛ-1.

Экспериментальные результаты, как мы считаем, находятся в хорошем согласии с теоретическими данными. Некоторые отличия экспериментальных данных для Lc от теоретических можно объяснить следующими соображениями. В наших экспериментах мы использовали весь спектральный диапазон излучения Na лампы, а не только излучение желтого дублета. Следовательно, в теоретических оценках зависимости Lc(0) необходимо учитывать влияние и других спектральных компонент излучения, влияющих на длину когерентности волнового поля. В спектре излучения наблюдался еще один дублет на длинах волн 0,5864 мкм и 0,587 мкм с интенсивностью линий в ~ 10 раз меньшей интенсивности линий основного дублеты и с полной шириной двойного контура ~ 0,0011 мкм. В теоретических оценках мы также не учитывали различия в интенсивностях линий дублета. Отличия экспериментальных данных от теоретических могут быть также обусловлены, как мы считаем, влиянием существенно ограниченной поперечно й когерентности поля в результате возможных поперечных смещений интерферирующих полей при продольном сканировании зеркала интерферометра, вызванных неточностью юстировки интерферометра и расположения апертуры фотодетектора на оптической оси интерферометра. Например, при 0=0,1 радиус поперечной ко- герентности равен ρ ⊥ ≈ λ/ 2θ ≈ 3 мкм. Поперечный сдвиг волнового поля в ∆x ≈ 0,5ρ⊥ при продольном сдвиге ∆z ≈ 150÷ 300 мкм вполне вероятен и приводит к заметному сужению наблюдаемого интерференционного импульса [11]. Необходимо также учитывать интегрирующее влияние конечной апертуры фотоприемника, которое при больших разностях хода заметным образом сужает интерференционный импульс в сигнале интерферометра [33].

Заключение

Длина когерентности оптического поля в продольном направлении – в направлении распространения поля – в общем случае определяется и частотным, и угловым спектрами этого поля. Для узкого углового спектра (для направленного пучка света) длина продольной когерентности определяется преимуществ енно частотным спектром, вернее, его шириной. Для поля с широким угловым спектром и достаточно узким частотным спектром длина продольной когерентности преимущ ественно определяется шириной углового спектра. На продольную когерентность одинаковым образом могут влиять и частотный, и угловой спектры поля. В свободном пространстве излучения протяженного некогерентного источника всегда найдет ся такая область, в которой продольная когерентность в равной степени определяется и частотным, и угловым спектрами поля. В этой области длина продольной когерентности одновременно оказывается существенно зависимой и от ширины частотного, и от ширины углового спектров поля. Эта зависимость длины когерентности от ширины частотного и ширины углового спектров в аналитическом виде получена в настоящей работе. Получены также выражения для функц ии продольной когерентности оптического поля с широкими угловым и частотным спектрами.

С длиной продольной когерентности поля связано широко используемое представление о волновом цуге. Если длина продольной когерентности определяется преимущественно угловым спектром оптического поля, L_c ≈ ρ II , то с необходимостью приходим к представлению о непрерывно и стохастически изменяющемся волновом цуге в процессе его распространения. При L_c ≈ l_c , как показано в [13,15], волновой цуг пробегает без существенных декорреляционных изменений расстояние ∆ z ≈ ρ || . Это расстояние можно рассматривать как длину коррелированного (свободного) пробега волнового цуга. В дальней области дифракции, для которой волновое поле имеет узкий угловой спектр, длина коррелированного пробега волнового цуга устремляется в бесконечность. Однако вблизи поверхности источника эта длина пробега сравнима с длиной временной когерентности l_c , а еще ближе к источнику эта длина становится меньше l_c и определяет длину самого волнового цуга, который уже имеет длину коррелированного пробега меньше длины самого цуга.

В интерференционном эксперименте необходимо рассматривать и учитывать зависимость продольной когерентности и от частотного, и от углового спектров поля. Эта зависимость может проявляться в различных экспериментальных условиях, например, в микроскопии высокого разрешения, в том числе в интерференционной микроскопии, когда используются объективы с большой числовой апертурой и широкополосный источник света [16,17,34-36]. В этом случае в интерференционном явлении участвует поле с широкими угловым и частотным спектрами, определяющими длину его продольной когерентности. Полная длина продольной когерентности может проявляться и в методе формирования совпадающих изображений (ghost imaging) [26,27] при использовании частично когерентного излучения протяженных тепловых источников.

Результаты настоящей работы, как мы полаг а-ем, имею т и в ажно е методо логич еское значение, уточ няющ ее соответствующие по ло жения теории когерентности оптич еских по лей и теории прояв -ления когерентности в интерференционном эксперименте.

Авторы работы благодарят А.Л. Кальянова, Л.А. Максимову, О. А. Перепелицыну за помощь в экспериментальных исследованиях. Работа выполнена при поддержке грантов аналитической ведомственной целевой программы «Развитие научного потенциала высшей школы», коды проектов 2.1.1/4364 и 2.2.1.1/2950 и гранта Президента для поддержки ведущих научных школ РФ НШ-208-2008.2.