Продольно-поперечные геометрически нелинейные волны деформаций

Задача определения напряженно-деформированного состояния полупространства при действии на его поверхности изменяющихся во времени нормальных p ( t ) и касательных q (t ) нагрузок (рис. 1) сводится, вообще говоря, к определению параметров продольно-поперечных волн деформаций, распространяющихся в сплошной среде.

Для сплошной среды, механическое поведение которой описывается уравнениями теории пластического течения, либо уравнениями динамики грунтов С. С. Григоряна, либо уравнениями билинейной теории пластичности, обзор решений данной задачи изложен в монографии [3].

G * ( е * , Г * ) - геометрически-нелинейный аналог модуля сдвига.

Пусть на поверхности полупространства действуют равномерно-распределенные нагрузки, бесконечно протяженные в направлении осей у и z (см. рис. 1). Полупространство будет находиться в условиях плоской задачи:

u = u ( х ), v = v ( х ), w = 0.            (2)

Тогда [1]:

*

8x

9 u   1

9 х 2

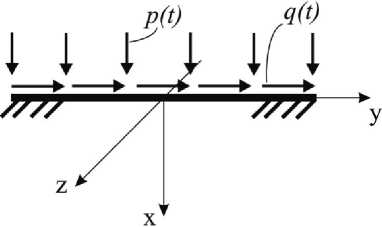
Рис. 1

⁸ у

9 v 1 =— + —

.*

xy

⁹ у

*

yx

9 u

^{2   9} у

[г I² к⁹ у

= 0,

9 u 9 v

9 u 9 u

9 v 9 v 9 v

=    +---+       +---=--

9 у 9 х 9 х 9 у 9 х 9 у 9 х

*         * .     *         *

При этом 8 = 8 + 8 = 8 , xyx

= У**у ^{( х )} .

В данной работе рассматриваются сплошные среды, механическое поведение которых описывается геометрически-нелинейными аналогами произвольных перекрестных зависимостей между первыми инвариантами тензоров о * и е * и вторыми инвариантами девиаторов T * и Г * обобщенных напряжений и деформаций:

о * = 3 К(е * , Г * ) е * ; Т * = G * (е * , Г * ) Г * , (1) здесь К *( е * , Г * ) - геометрически-нелинейный аналог модуля объемного расширения (сжатия), © Бакушев С. В., 2014

Г* = V 4 (=. )2+3 (/X, у )2 /V3.

Физические уравнения для геометрически-нелинейной модели сплошной среды имеют вид:

*                         *      *„* *

а_х = K + ~G 8 ; т = G У ;

xxyxy к      3

ау = | K* -2G* 8*; т*z = 0;

к     3у

* TZ* ^ * **

^az = K —G 8 ; т^ = 0.

zzx к 3 у

Подставляя соотношения (5) в динамические уравнения равновесия без учета объемных сил

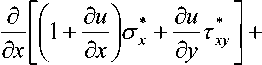
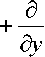
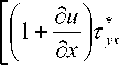
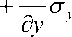
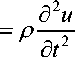
а дх

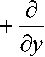
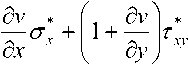
получаем систему четырех дифференциальных уравнений первого порядка в частных производных относительно величин

Ф  Ф д Vx д vy . '^ дУу д Vx дx ’   дx  ’ д t ’ д t  ’   д t  ’ д t  ’ дx

В матричной форме система уравнений (7), (10)

имеет вид:

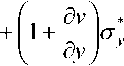
d"v

ди ди

А — + В— = 0.

дх at

Здесь матрицы A и B равны:

и учитывая зависимости (1) и (4), получим два уравнения, описывающих процесс распространения продольно-поперечных геометрически-не-линейных волн деформаций:

Ф + Ф^ + 5)<^=p^p

OX ot

^ + £хЪх_УА + С^^ ■ ox

xvWxv + Ф lC/ху + Г»)}^ = Р^ ■        '                   ■ ox ot

Здесь введены обозначения:

д и

д v

д и

Е =-- V =-- V =-- V x   дx ’   /xy   дx ’ x д t ’ y

co, 8x

^. (8) д t

аи ар 00

А =   222

0  0-1о ’

0   0   0-1

"0   0 -рО’

О 0   0

в=,

10  00

0  100

причем

«11=к+4С7з)Г + (г;+/|,.)/2]+ + 0 + ^ )2 ^;

«и =(i + ^)UrXv +5);

«21 =(1 + ^)ки + ^с);             (12)

Значения коэффициентов A , B , C , D равны:

ак 4 ас

ds 3 дг

дК 4 дС

ЗГ

аг* заг* ’

ак 4 ас

г

аг* заг* ’

«22 - (^ + 4G /з)^ + (^f + /|_v)/2] +

+ Уху^Гху +_^в)+ (^с Уху + 79).

Вектор-столбец u имеет следующую структуру: u _Г ^ к,   v_x   V_v Т.

xxy x y

Характеристические кривые уравнения (11) определяются путем решения уравнения | A - ^ B| = 0 или в развернутой форме:

Л'Т

ас 45 ас as* зг* аг

D = G*

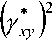
ac*

« 11	« 12	ap	0
a 21	« 22	0	ap	_ 0 ,
-a	0	-1	0
0	-a	0	-1

r* ar*’

Присоединяя к уравнениям (7) уравнения совместности

вещественные решения которого задают характеристические кривые, описываемые дифферен-

Эе   dv     ду   dv

°х _ vx      • xy _ y_ д t    дx ’ д t     дx ’

циальными уравнениями:

aij

dx

, i 1,²; j 1,2. dt

Здесь

Пусть го ( x , t ) = 0 - уравнение поверхности разрыва [4]. Применяя кинематические условия сов-

« 1,1   ⁺ V M 1 / ^{( 2 р )} ,

« 1,2    V ^M 1 /^{( 2 р )} ,

местности

« 2,1 - + M^ ^ 2 р ) ,

« 2,2 ^- -7 M 2 /(² Р ) ,

д ² и д x j д x _k

дю дю .

--2 к системе (18),

u дxj дxk

получим динамические условия совместности:

причем

^M 1,2    ⁽ a 11 ⁺ a 22 ⁾ — \⁽a 11   a 22 ^{) + 4} a 12 a 21 - (14)

Дифференциальные уравнения (13) определяют, вообще говоря, четыре семейства характеристических кривых. Система уравнений (7), (10) будет гиперболического типа, если все a i j будут вещественными. ^,

Найдем соотношения вдоль характеристических направлений. Введем вектор l = [ 1 1 1 ₂ 1 ₃ 1 ₄]. Компоненты вектора l являются решением уравнения l • ( A - « В ) - 0 , откуда находим:

( а _п - а ² р ) • 1 1 + a ₂₁ • 1 ₂ - 0;

( a ₂₂ - а ² р ) • 1 ₂ + а ₁₂ • 1 1 - 0;

13 - ар • 11 - 0;

1 ₄ - ар- 1 ₂ - 0.

Соотношения вдоль характеристик найдем на

-   ( d u )

основании уравнения l • В • --- - 0, откуда dt

1 ^dp + 1 d ^ xy dt dt

dv

a

^а 21

^- р¹ 1 "v ^- р¹ 2 v ^{- 0- (16)} dt dt

Используя далее зависимости (15), уравнение (16) приведем к виду:

а 21 ( « ² р ^- а 22 ) ( « " ^ ^- "v .) ⁺

+ а ( а ² р - а₁₁ )( « ² р - а ₂₂ ) d y xy - а₁₂а ₂₁ dv _y - 0.

Итак, вдоль четырех семейств характеристик (13) выполняются соотношения (17).

Запишем систему уравнений (7), (10) в терминах перемещений. Используя соотношения (8), систему (7) приведем к виду:

д2 и      д2 v     д2 и а" а?+а'2 э? - р а?;

д2 и      д2 V     д2 V а21 3? + а22 5? = ^-I

Система (10) при этом удовлетворяется тождественно.

2 дю У удxj

² дю А 2 _у д x j

2 д ю А ²

- р     I уд t J

² и ^{+ а} 22

² и ^{+ а} 12

2 дю У _у д x j

2 дю ) .

—— 2 д x J

2 д ю А ²

- р     I уд t J

- 0;

((19) - 0.

Поскольку значения скоростей распространения волн N по нормали к фронту определяются соотношением:

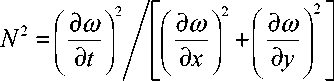
а направляющие ко синусы 1_i вектора нормали к фронту волны в локальной системе координат, совпадающей с главными осями, равны

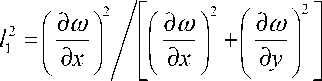
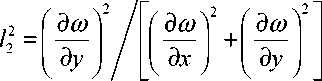
то система (19) после элементарных преобразований получает вид:

( а ,, 11 - Р N ² ) 2 „+ а ,2 11 2 . _; - 0;

«112, + ( а_и1 ,² - Р N² ) 2 - 0.

2 1 1 U |          22 1                     U ^

Приравнивая к нулю определитель системы (20), то есть полагая для коэффициентов прерывности ² и ₁ и ² и ₂ существование ненулевых решений, получим:

f (20)

2 р №₂ - 1 1² ( а 11 + а ₂₂ )±7( а 11 - а ₂₂ ) ² + 4 а ₁₂ а ₂₁

Формула (21) определяет две независимые скорости распространения продольно-поперечных волн деформаций в сплошной среде.

Выпишем коэффициенты, входящие в формулы (19) и, соответственно, в формулу (21). При этом буд ем помнить, что в главных осях

*                     ду*         ду„

Y xy ^- Y yx ^{- 0} , однако — xy- ^ 0 и —— ^ 0 .

дx       ду

Кроме того, для данной задачи у _{х у} - y xy .

На основании соотношений (4) получаем ^е j^ = ^3/4 . Теперь коэффициенты A , B , C , D ,

определяемые соотношениями (9), будут равны:

Случай 1 . Пусть l ₁ = 1, l ₂ = 0, то есть главное направление x ₁ совпадает с направлением нормали к фронту волны ( α = 0). Система (20) получает

+

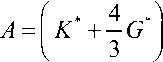
Г дк * ^дГ *

д К * де*

4 д G * ^ ⁺ 3 де .

4 д G *)

3 дГ* ,

Г * ;

B = 0; C = 0; D = G * .

Следовательно,

a 11

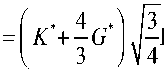
д к * 4 д G * ) /3 * ^де ⁺ 3 де J 44 ^{1 +}

^дК^ 4 д G* ' ^дГ * ⁺ 3 дГ * ,

a,2 = 0;  a21 = 0;

a 22

Г* + G *.

3Г*+

Г *

+

; (22)

С учетом соотношений (22) формула (21) получает вид:

2 p N 2 = Г; ( 2 a , ) ; 2 p N 2 = l f ( 2 a 22 ) . (23)

Рассмотрим условия возникновения и распро-

странения чисто продольных и чисто поперечных волн деформаций.

В локальной системе координат, совпадающей

в каждой точке сплошной среды с направлениями главных деформаций (напряжений), введем вектор X с составляющими ( A u , Au^ ) в каждой

точке сплошной среды. Пусть λ_n – проекция вектора λ на нормаль к переднему фронту волны

(рис. 2), то есть A n = A u I, + A u J ₂ , где l , = Cos ( a ), l ₂ = Sin ( α ); l ₁ и l ₂ – направляющие косинусы нормали к переднему фронту волны.

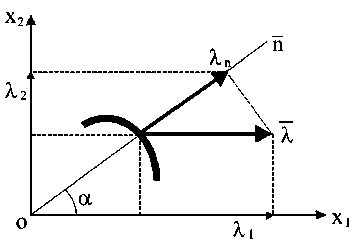
Рис. 2

вид:

( a _n - p N ² ) ^A u , = 0;

( a 22 ^- p N ² ) ^A u 2 = 0.

Отсюда получаем: N , ² = a ,,/ p , N ₂ ² = a ₂₂/ p .

Рассмотрим распространение волны N1. Если N = N1, то система (24) приводится к виду:

0 • A„,= 0;

( a 22 - p N ² ) A . 2 = 0,

то есть так как a ₂₂ ^ p N , ² , то Au₂ = 0 . Это означает, что из двух составляющих вектора λ одна равна нулю, то есть проекции A n и A u совпадают с самим вектором λ , то есть главное направление x ₁ и нормаль к фронту волны n ^– совпадают с вектором скорости N ₁. Имеет место чисто продольная волна.

При рассмотрении распространения волны N ₂, то есть N = N ₂, система (24) получает вид:

(a,, -pN2)A.,= 0;'

Г

0 • A = 0.

u ₂

Это означает, так как a ,, ^ p N 2 , что A u = 0 , то есть проекции A n и A u совпадают с самим вектором λ . Следовательно, главное направление x ₁ и нормаль к фронту волны n ^– перпендикулярны к вектору скорости N ₂. Имеет место чисто поперечная волна.

Случай 2 . Пусть l ₁ = 0, l ₂ = 1, то есть главное направление x ₂ совпадает с направлением нормали к фронту волны ( α = 90°). Система (19) полу-

чает вид:

-pN2 A = 0;

u ₁

-pN2 A = 0.

u ₂

Отсюда следует, что N = 0, то есть в направлении главного направления x ₂ волна не распространяется.

На рис. 3 показаны векторные диаграммы мгновенных скоростей продольно-поперечных геометрически-нелинейных волн деформаций, построенные по уравнениям (23) для трех математических моделей сплошной среды.

Модель 1 . Механическое поведение сплошной среды описывается линейным законом, то есть деформационные зависимости (1) имеют вид:

σ ^* = K ₀ ε ^*; T^* = G ₀Г^*. (26)

Модель 2 . Механическое поведение сплошной среды описывается квадратичным законом в от-

ношении сдвиговых деформаций. Деформационные зависимости (1) в этом случае равны:

σ ^* = K ₀ ε ^*; T^* = G ₀ (1 – Г^*/ (2Г _s )) Г^*.     (27)

Модель 3 . Механическое поведение сплошной среды описывается перекрестными зависимостями между инвариантами напряженного и деформированного состояний:

a = K о [ 1 - ( q/ г )( 2 -Г/Г , ) 2 ( Г/Г , ) 2 ] г;

T = [ G о ( 1 - Г * /( 2 Г , ) ) + K ₀ f ( ql Г , ) ( 2 - Г */ Г , ) 2 ( г */ Г , ) -

• - K о f (г/ Г * ) ] Г * .                (28)

Модель 1 соответствует геометрически-нели-нейному аналогу линейной теории упругости, модель 2 соответствует геометрически-нелиней-ному аналогу теории малых упруго-пластических деформаций, модель 3 соответствует геомет-рически-нелинейному аналогу деформационной теории пластичности сыпучей среды [1], [2].

На рис. 3 сплошная линия соответствует приведенным скоростям 2 p N 2 G ₀ , пунктирная -скоростям 2 p N 22 G ₀ .

В формулах (26), (27), (28) имеем: K ₀ – начальный модуль объемного расширения (сжатия); G ₀ – начальный модуль сдвига при чистом сдвиге; f – аналог коэффициента внутреннего трения; q – коэффициент дилатансии; Г _s – предельная интенсивность деформаций сдвига, причем 0 ≤ Г^*/ Г_s ≤ 1.

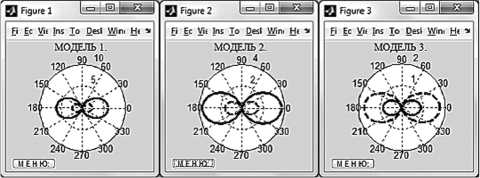
Рис. 3. Векторные диаграммы мгновенных скоростей продольно-поперечных геометрически-нелинейных волн деформаций

Исходные данные:

K ₀/ G ₀ = 1,1547; q /Г _s = 1; Г^*/Г _s = 0,75;

Г _s = 0,1155; f = 0,5.

Численные исследования показывают, что скорости распространения продольно-поперечных волн деформаций существенно зависят как от рассматриваемого направления распространения волны, так и от уровня напряженного и деформированного состояния в рассматриваемой точке среды, а также от величины физических констант материала сплошной среды.

Изложенные в статье результаты могут быть использованы при построении алгоритмов расчета напряженно-деформированного состояния геометрически и физически нелинейных полупространств, находящихся в условиях плоской деформации, от действия на поверхности динамических, в том числе ударных, нагрузок.

LONGITUDINAL-CROSS GEOMETRICAL NON-LINEAR WAVES OF DEFORMATION