Продольно-поперечный изгиб статически неопределимой балки, создаваемый эллиптическим пуансоном
Автор: Юрьева Валентина Леонидовна, Сайманов Равиль Гакифович
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Машиностроение и машиноведение
Статья в выпуске: 6-1 т.19, 2017 года.
Бесплатный доступ
В статье представлен метод расчета растянуто-изогнутой балки с защемленными концами, которая на участке соприкосновения с пуансоном изгибается по дуге эллипса. Проведенные исследования условий контакта балки с пуансоном показали, что если концы балки могут перемещаться в осевом направлении, то контакт балки с пуансоном будет только в двух крайних точках или небольшой зоне около них, а между балкой и пуансоном будет просвет. Для того, чтобы был возможен контакт балки с пуансоном по всему участку, необходим осевой натяг балки. Полученное решение использовано для расчета разъемного гиперболоидного контакта радиоэлектронного оборудования летательных аппаратов. Проволоки гиперболоидного разъема представляют собой балки с защемленными концами, расположенные под углом к оси штекера. Давление на проволоку будет по дуге эллипса. Предлагаемый метод расчета позволяет определить величину и область приложения усилия контактного нажатия, наибольшее напряжение и осевую силу в проволоке. Рекомендовано предварительное натяжение проволок гиперболоидного разъема, что позволит существенно повысить его надежность.
Балка, пуансон, натяг, продольно-поперечный изгиб, гиперболоидный разъем, контакт
Короткий адрес: https://sciup.org/148205392
IDR: 148205392 | УДК: 629.7.05:620.10
Текст научной статьи Продольно-поперечный изгиб статически неопределимой балки, создаваемый эллиптическим пуансоном
М.Е. Лурье [17], А.Р. Ржаницына [18], С.П. Тимошенко [19] и многих других.
Разработка методов расчета балок на продольно-поперечный изгиб явилась предметом внимания многих исследователей ввиду большого практического значения этого вопроса.
Анализ работ, посвященных продольно-поперечному изгибу, показывает, что в строительной механике нет общего метода расчета балок, работающих на изгиб с растяжением, доведенного до удобных при практических расчетах алгоритмов и схем.
Особенность рассматриваемой нами задачи заключается в том, что неизвестными являются величина контактного давления на балку, закон его распределения по длине, область приложения, а также величина осевой силы, возникающей в балке. Кроме того, задача должна быть решена с учетом предварительного натяжения балки. Известными являются геометрические размеры балки и ее максимальный прогиб, который ограничивается конструкцией. В такой постановке задача не решалась.
В настоящей статье представлен разработанный нами метод расчета растянуто-изогнутой балки с защемленными концами, которая на участке соприкосновения с пуансоном изгибается по дуге эллипса. Расчетная схема представлена на рис.1.
В основу предлагаемого метода расчета положены следующие допущения:
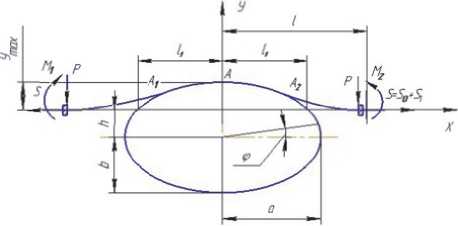
Рис. 1. Расчетная схема балки
-
1. Деформация балки упругая и малая.
-
2. Концы балки жестко защемлены.
Проведенные исследования условий контакта балки с пуансоном показали, что если концы балки могут перемещаться в осевом направлении, то контакта балки с пуансоном по всей длине 2 1 1 не будет. Контакт будет только в двух некоторых точках А 1 и А2 (рис. 2) или в небольшой зоне около этих точек.
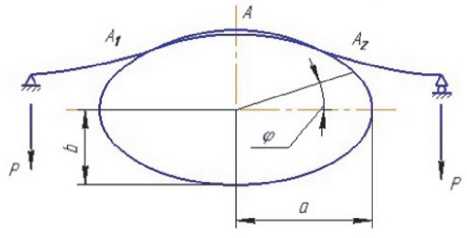
Рис. 2. Контакт балки с пуансоном
Действительно, рассмотрим случай, когда большая ось эллиптического сечения пуансона параллельна оси балки. Радиус кривизны эллиптического сечения пуансона записывается следующим образом:
R = — (a2 sin2 ф + b2 cos2 ф)2, ab где ф - угловой параметр; а и b - полуоси эллипса.
Радиус кривизны эллипса будет иметь наибольшее значение при ф = п/2, а наименьшее - при ф = 0. То есть, на некотором участке предполагаемого контакта А1А2 кривизна при удалении от точки А1 (или точки А2) в сторону точки А уменьшается. Допустим, что на участке А1А2 балка опирается на пуансон. Тогда на этом интервале изгибающий момент M = EI/R должен уменьшаться с приближением к точке А, как и 1/R. Но, возможно ли это? Изгибающий момент в сечениях балки до точки А1 слева растет, а после точки А1 по какому-то закону должен падать. Следовательно, в этом случае в точке А1 будет излом эпюры М, а это возможно, если в точке А1 приложена сосредоточенная сила. Если эта сила меньше реакции Р в опоре, то ординаты эпюры М за точкой А1 вправо будут после излома сно- ва возрастать. Но это противоречит допущению. Если сила, действующая в точке А1 равна реакции в опоре, то на участке А1А2 изгибающий момент должен быть постоянен, что тоже противоречит допущению. Случай, когда сила, действующая в точке А1 больше реакции в опоре невозможен, так как не будет выполняться условие равновесия балки.
Иначе говоря, допущение о том, что балка облегает плотно пуансон на всем участке А1А2 при подвижном закреплении ее концов, ошибочно. На интервале А1А2, кроме самих точек А1 и А2 и, возможно, небольшой зоны около них, между балкой и пуансоном будет просвет (рис. 2).
Подобное явление отмечают и другие авторы. Так, в работе В.М. Толкачева [20] рассматривается контактная задача для сферической оболочки. Автор строго математически доказал, что контакт тонкой упругой сферической оболочки и жесткого штампа происходит по круговой линии, ограничивающей зону контакта. Средняя же часть оболочки не прилегает к штампу.
В работе Л.А. Галина [21] рассмотрен вопрос о давлении твердого тела на тонкую пластинку. Им также доказано, что давление, действующее на площадке контакта, приложено по контуру.
Для того, чтобы был возможен контакт балки с пуансоном по всему участку А 1 А2, необходим осевой натяг балки. Такой натяг балки появится при неподвижном закреплении ее концов, и может быть увеличен за счет предварительного натяжения балки.
Решение поставленной задачи получено интегрированием дифференциального уравнения упругой линии балки.
Изогнутая ось балки на участке соприкосновения ее с пуансоном будет представлять собой дугу эллипса, уравнение которой y 1 = ~ V a 2 - x 2 -(b - y max ), (1) a где a, b - полуоси эллипса; ymax - максимальный прогиб.
На участке свободном от внешней нагрузки изогнутую ось балки получим интегрированием соответствующего линейного неоднородного дифференциального уравнения y2 - %2y2 =-A - B(l- x), (2)
где А = - M/EI , B = - P/EI , х 2 = (S0+S 1 )/EI .
Здесь М - изгибающий момент; 2Р - усилие контактного нажатия на балку; S0 - осевая сила от предварительного натяжения; S1 - осевая сила от изгиба; Е - модуль продольной упругости; I - момент инерции поперечного сечения балки.
Общий интеграл уравнения (2)
А + B ( l — x )
y 2 = C , ch % x + C 2 sh % x +------ 2---- , (3)
x содержит пять неизвестных величин: константы интегрирования С1 и С2, а также A, B и %. Кроме того неизвестна длина линии контактна 2l1 балки с пуансоном.
Для определения неизвестных величин используем граничные условия задачи:
при x = l 1
У 1 = У 2 ,
f I bx
J r~2 2
a V, a v a - x
) 2 dx +
J
+ J C 1 X sh X x + C 2 X ch X x - 1 1 V
в L sj
— dx - 2^.
X 2 J
Sl
EF
dy 1 - dy 2
dx dx d2 У i - d2 У 2 .
dx 2 dx 2
Из уравнений (8) и (9) следует
A - - ( c 1 X 2 ch X l + C 2 X 2 sh X l ) , (11)
B - C 1 X 3 sh X l + C 2 X 3 ch X l . (12)
Условия (6) и (7) с учетом уравнения (12) дают:
C 1 -
b
-------/ -------------------x
X 2 a > 2 - 1 1 2 [ 1 - ch X ( l - 1 1 ) ]
при x = l
У 2 = 0 ,
X
d^ = 0 dx
и условие отсутствия сближения конусов балки в процессе деформации
l
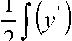
a
где F – площадь поперечного сечения балки.
С учетом зависимостей (1) и (3) граничные условия запишутся так:
-Jo--"^ - ( b - y max ) - C 1 ch x l 1 + a
+ C 2 sh % l i +
A + B ( l - 1 1 ) XX
bLR
---P=L= - C1 shxl 1 + C 2 chxl 1 - —,
Xa^a 2 — 112
ab l21
= - C 1 c h X l 1 + C 2 sh X l 1 ,
2a ,2 ( ch X l - ch X l 1 ) + X l 1 sh X l 1 a - 1 1
C 2 -
-
-------/ -------------------x
X 2 a Да 2 - 1 1 2 [ 1 - ch X ( l - 1 1 ) ]
X
——-( sh X l - sh X l 1 ) + X l 1 ch X l 1 a - 1 1
Подставим выражения для С1 и С2 в уравнения (11) и (12). Тогда
. b aг
A - гч—^ - аДа -112 L a -11
B -
-
sh X( l - 1 1 )
X l1 1 - ch X l - l 1 ) l ’
________Xb________ aVa2 - l 12 [1 - chX(l- l 1)]
X
a2 a 2 -
A
C 1 ch x l + C 2 sh x l + - - 0 , X 2
—sh X( l - 1 1 )+ X l 1 ch X( l - 1 1 ) . l 1
B
С 1 sh X l + C 2 ch X l - —г - 0 , X 3
а условие (4) –
Зависимости для определения A,B,C1,C2 выражены через два неизвестных параметра – и l 1. Для их определения используем оставшиеся условия (5) и (10). После преобразований придем к уравнениям вида:
2 a ,2^ Ь - y max 7 a 2 - 1 12 )_
+ a — 1 1 =
X ( a - 1 1 ) b
x ^ 1 1
-
+ <
x ^
X [ 1 - ch X( 1 - 1 1 )JX
a 2
a 2
-
l
x
2 a ,2 s h X( l — 1 1 ) + X l 1 ch X( 1 — 1 1 ) a — 1 1
. (16)
( l - l 1 ) sh x l ( 1 - 1 1 )
-
- Z l i ( 1 - 1 1 ) ch! Z( 1 — 1 1 ) " , (13)
_ X ( a
b
2 a
—
, a + L2
In-----1
a — 11
ab
+
Однако решить систему трансцендентных уравнений (13) и (14) аналитически не представляется возможным. В математической литературе вопрос о решении таких уравнений затронут мало.
Для отыскания действительных корней системы трансцендентных уравнений в случае, когда решение не может быть получено в явном виде, применяются приближенные методы (графический способ, способ Фурье, метод подбора корней, способ Ньютона, метод итерации), даю-
a 2
—
1 2 [ 1 — c X — 1 1 ) ] ,
> x
2 sh %( 1 — l 1 )
—
— sh 2 x ( 1 — 1 1 ) — ( 1 — 1 1 ) x X
x [ 1 — ch X ( 1 — 1 1 ) — sh2 X( 1 — 1 1 ) ] + X 1 1 a 2 1 1 x a
x ((1 — 11)[shx(1 — 11)+ sh 2x(1 — 11)] —
— — sh2 x ( 1 — 1 1 ) + — chx ( 1 — 1 1 ) x XX
x [1 — chx(1 — 11)]) +
x
2 + ch 2 x ( 1 — 1 1 )
X 1 1
—
a 2 — 12
a 2
0,75
X
( ( 1 — 1 1 ) X
sh 2 x ( 1 — 1 1 )
sl
2 = 0.
EF
Уравнения (13) и (14) – трансцендентные. Решая их совместно, можно определить неизвестные параметры и l 1 . Определив их, используя зависимости (2) и (3) и выражения для А и В, найдем усилие контактного нажатия 2Р на длине его действия 2 l 1 , осевую силу в балке, деформацию и напряжения в сечениях балки. Так, наибольшее напряжение в балке запишется
уравнением:
^ max
5000 db
a
a2
^^^^^^^B
^^^^^^^B
X l 1
sh X( 1 — 1 1 )
1 — chX(1 — l 1)
+ 625 X 2 d 2.
Усилие контактного нажатия на балку равно
4 yh
2 P = 981,25 . X ----------x
a ya2 — l2 [1 — chX(l— l 1)]
щие возможность получить численные результаты. В теоретическом отношении упомянутые способы хороши, но практически для решения системы уравнений типа (13) и (14) ими пользоваться неудобно: они слишком громоздки.
При решении системы трансцендентных уравнений на ЭВМ наиболее удобен метод итерации. Однако, при этом трудно найти достаточно близкие к точным исходные приближенные значения корней, и поэтому не всегда удается добиться сходимости процесса. Эта первоочередная задача решается либо графическим способом, либо методом подбора корней.
В литературе по численному анализу не да-
ется строгого и полного ответа на вопрос о том, каковы необходимые и достаточные условия
сходимости процесса итерации при решении
системы уравнений.
Численное решение уравнений (13) и (14) с заданной точностью было получено методом ускоренной итерации Зейделя. Приближенные значения корней определены предварительно графическим способом.
Уравнения (13) и (14), при решении их методом итерации, удобно записать в виде:
X = —
— a 7^!,7 ( 1 — 1 1 )
[ 1 — ch X ( l — 1 1 )]
- x
xF
sh X ( 1 — 1 1 ) — X l 1 ( 1 — 1 1 ) ch X ( 1 — 1 1 )
2 a 2
X 2 ( a 2 — 1 12 )+
+
X ( a a
^^^^^^^B
—
( Ь — У max ) « V
a 2 —
=й, (17) 1 12
b
, a, a + 1
1 1 = -In 1 +
2 a — 1 1
a2
a 2 — 1 1 2 [ 1 — ch X( l — 1 1 ) ]
-i 2
x
x <
3 , s z
3 sh X ( l — 1 1 ) — sh 2 X ( l — 1 1 ) —
2 X
-( l - l i ) [ i - ch x1 - l i ) - sh 2 X( 1 - l i ) ]+
+ X 1 a1 ( 11 - 1 i ) [ M - 1 i ) + sh 2 X l - 1 1 ) ] - a
- —sh 2 x ( 1 - 1 1 ) +— ch x ( 1 - 1 1 ) x
X
X a2 -
r x [ i - ch x ( -1 i ) ] + X 1 i
V x[0,5 + ch2 x(1 -11)]-075 X a a
l l |2
J
sh 2 X ( 1 - 1 1 )) '
^^^^^^^e
\ 2Г a 1 b J 1
0,i25 x2d - 0,0002547 s0.1 . (18) d 2
Отыскиваем корни первого приближения х и l 1 графическим путем по уравнениям (17) и (18). Для этого задавшись значением х = Х 1 , подбираем такое l 1, которое с точностью до 0,00000001 удовлетворяет уравнение (17). Такая операция проделывается для ряда значений х и по полученным результатам строится зависимость f(х, 1 1 ) для уравнения (17).
Подобным образом поступаем с уравнением (18), т.е. задавшись значением l = l 1, подбираем величину х , котораяс точностью 0,00000001 удовлетворяет уравнению (18). Повторив эту операцию несколько раз для различных значений l 1, строится зависимость ф ( х , 1 1 ). Пересечение кривых f ( х , 1 1 ) и ф ( х , 1 1 ) дает искомые корни х и 1 1 .
Использование полученного решения покажем на примере расчета разъемного гиперболоидного контакта радиоэлектронного оборудования летательных аппаратов.
Гиперболоидный разъем представляет собой устройство, использующее прямолинейные образующие гиперболоида вращения в качестве активного элемента контактной пары. Конструктивно гиперболоидный разъем состоит из гильзы 1, втулки 2, хвостовика 3, проволок 4 и штекера, (рис. 3).
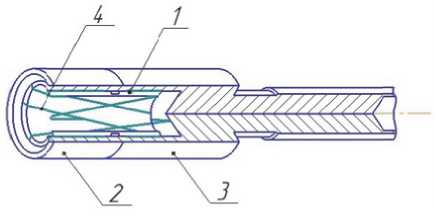
Рис . 3. Конструкция гиперболоидного разъема
Проволоки устанавливаются на внутренней поверхности гильзы под углом к образующей цилиндра. Концы проволоки загнуты на наружную поверхность гильзы и жестко защемлены с одной стороны втулкой, а с другой хвостовиком. Про- волоки образуют внутреннюю контактирующую поверхность гнезда переменного по длине кругового сечения: у основания гильзы сечение наибольшее, а в середине – наименьшее (горловина гиперболоида). Диаметр горловины меньше диаметра штеккера. При введении цилиндрического штекера в гнездо, каждая проволока деформируется и давит на его поверхность (рис. 4).
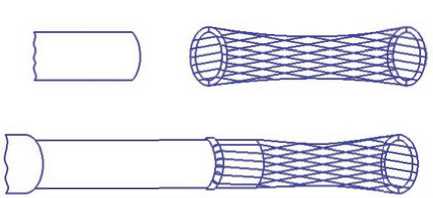
Рис. 4. Штекер и гнездо
Совершенно очевидно, что одним из важнейших условий, определяющих надежность работы контактов и рациональность их размеров, является выбор параметров конструкции из условия прочности и жесткости ее элементов.
Предварительные исследования, которые предшествовали выбору расчетной схемы, показали, что соотношение размеров используемой в гиперболоидных разъемах проволоки те же, что и у обычных строительных балок.
Следовательно, при расчете проволоку нельзя представлять в виде гибкой нити, как это кажется на первый взгляд. Проволока будет работать как балка. Концы проволоки защемлены неподвижно, поэтому при давлении штекера на проволоку в ее сечениях кроме изгибающих моментов возникают еще и растягивающие силы. К тому же, для обеспечения лучшего зажима штекера, контактные проволоки должны иметь предварительное натяжение.
Расчетная схема проволоки гиперболоидного разъема представляется в виде растянутоизогнутой балки (рис. 5).
Так как направление оси проволоки гиперболоидного разъема составляет с осью штекера угол у , то участок проволоки некоторой длины 2 l 1, соприкасающейся со штекером, будет представлять собой дугу эллипса.
При расчете предполагаются известными геометрические размеры гиперболоидного разъема: диаметр гильзы D Г, диаметр штекера D Ш, диаметр проволоки d , глубина гильзы H , а также наибольшее отклонение проволоки при введении штекера y max (эту величину получают, исходя из габаритов контакта, с учетом необходимой ширины поля допусков на геометрические размеры), число проволок n , угол их наклона у .
Обычно, угол наклона проволок к образующей гильзы колеблется в пределах 6º…10º. Число проволок для наиболее распространенных типов контактов равно 6…16.
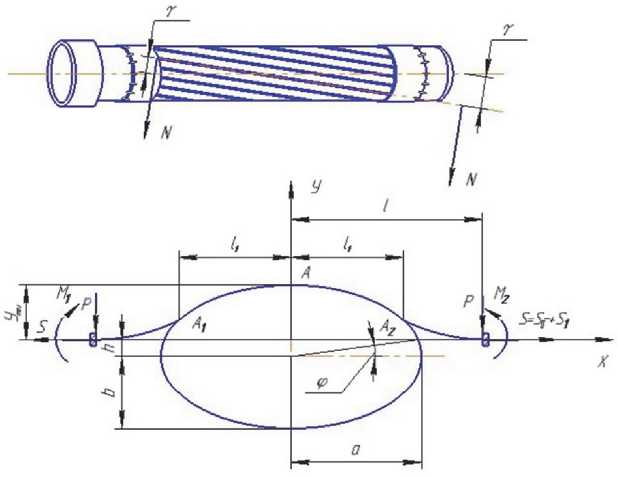
Рис. 5. Расчетная схема проволоки
Решение задачи изложено выше.
Пример.
d = 0,16 мм, D Ш = 1 мм, у = 6 o 35 ’ , 2 1 = 5,5 мм, у max = 0,03575 мм, S0 = 0,0192 кГ, Е = 1 . 106 кГ/см2.
Отыскиваем корни первого приближения
X и 1 1 графическим путем по уравнениям (17) и (18).
Пересечение кривых f ( х , l 1 ) и ф ( х , l 1 ) дает X = 0,352, l 1 = 0,340 мм .
Уточненные значения х и l 1 , полученные на ЭВМ методом ускоренной итерации Зейделя равны: х = 0,35197, l 1 = 0,33982 мм.
Определив х и l 1 , найдем величину наибольшего напряжения в проволоке (15) c max = 25,7 кГ/мм2 и усилие контактного нажатия (16) 2Р = 0,015 кГ.
ВЫВОДЫ
Гиперболоидный разъем с предварительным натяжением контактных проволок будет иметь следующие достоинства:
-
1. Надежный контакт на всей длине соприкосновения проволоки со штеккером.
-
2. Более равномерное распределение реакции в зоне контакта.
-
3. Равномерное распределение контакта нажатия между всеми проволоками разъема.
-
4. Повышение предела выносливости проволоки за счет замены пульсирующего цикла, изменения суммарных напряжений асимметричным.
-
5. Уменьшение необходимой стрелы прогиба при заданном контактном зажиме.
-
6. Увеличение контактного нажатия при заданной стреле прогиба, что способствует установлению лучшего контакта проволоки со штекером.
Получить равномерное распределение контактного нажатия между проволоками ненатянутыми или выпуклыми невозможно. Такая неравномерность будет вызывать перегрев отдельных пружинящих элементов и ослаблять их.
Этот вопрос имеет немаловажное значение, так как материал проволоки работает на усталость при многократных сочленениях.
Проектирование гиперболоидных разъемов с предварительным натяжением контактных проволок значительно повысит надежность таких конструкций.
Список литературы Продольно-поперечный изгиб статически неопределимой балки, создаваемый эллиптическим пуансоном
- Пузыревский Н.П. Основания и фундаменты (Литография), 1923.
- Дутов Г.Д. Расчет балок на упругом основании. Л.: Кубуч, 1929.
- Крылов А.Н. О расчете балок, лежащих на упругом основании. М.: АН СССР, 1930.
- Киселев В.А. Балки и рамы на упругом основании. ОНГИ, 1936.
- Снитко Н.К. Расчет сжато-изогнутого стержня при применеии общего уравнения упругой линии//Проект и стандарт. 1935. №5.
- Риппенбейн Я.М. Исследование сжатых и растянутых стержней на упругом основании//Сб. Исследования по теории сооружений. Вып. IV. М.: Стройиздат, 1949.
- Лунин В.С. О деформации прямолинейных стержней под действием продольных и поперечных сил//Вестник инженеров и техников. № 11…12, 1929.
- Герсеванов Н.М. Функциональные прерыватели и их применение в строительной механике//Труды ВВИА. М., 1935. Сб. №9.
- Завриев К.С. Основы теории функциональных прерывателей в применении к строительной механике//Тр. Тбилисского ин-та инж. ж.-д. транспорта. 1938. Вып. 6. С. 19-75.
- Вербовский Г.Г. О продольно-поперечном изгибе прямых двухопорных стержней. Труды ХИИЛТ, вып. 26, 1956.
- Макушин Р.М., Малинин Н.Н. Применение функций Весселя к задачам продольно-поперечного изгиба. Труды МИИГВФ, вып. 5, 1939.
- Киселев В.А. Уравнение упругой линии продольно-поперечного изгиба. М., МГИ, 1939.
- Макушин Р.М. Теория упругой линии при продольно-поперечном изгибе. Труды МВТУ, вып. 56, 1939.
- Урбан И.В. Общая теория продольно-поперечного изгиба в упругой среде. Труды МЭМИИТ, вып. 53, Трансжелдориздат, 1945.
- Глушков Г.С. Исследование упругой линии по способу автора.(Учебное пособие). М., 1932.
- Лебепов С.Ф. К вопросу о совместной работе на продольный и поперечный изгиб балок и колонн. Труда КАИ, вып. 46, 1953.
- Лурье М.Л. Построение эпюры моментов сжато-изогнутых балок постоянного сечения с помощью векторных диаграмм. Техника воздушного флота, № 5, 1930.
- Ржаницын А.Р. Графоаналитический способ определения деформаций сжато-изогнутых стержней. Труды МИСИ, № 2, 1939.
- Тимошенко С.П. Сопротивление материалов, ГНТИ, 1932.
- Толкачев В.М. Контактная задача для сферической оболочки. КФАН СССР, 1971.
- Галин Л.А. Контактные задачи теории упругости. М., ГТТИ, 1953.


