Продольное перемагничивание мультислойной ферромагнитной системы с немагнитной прослойкой

В современном научном мире большое внимание уделяется многослойным магнитным структурам, с помощью которых изготавливают магниторезистивные датчики, элементы магнитной памяти, спиновые диоды и т. п. В данной статье рассматриваются процессы перемагничивания многослойных магнитных систем, для исследования которых используется модель веерного вращения вектора намагниченности [1]. Объектом исследования является двухслойная магнитомягкая пленка с немагнитной прослойкой, в которой имеет место линейная зависимость намагниченности от внешнего поля, нанесенная на магнитожесткую подложку, обладающую прямоугольной петлей гистерезиса. Наличие такой подложки приводит к тому, что магнитомягкие слои будут характеризоваться неоднородным распределением вектора намагниченности по толщине пленки. Намагниченность подложки изменяться не будет, поскольку мы будем рассматривать поля меньше коэрцитивной силы подложки. В связи с этим магнитомягкие слои назовем просто ферромагнитными слоями.

В [1] исследовалась однослойная ферромагнитная пленка, нанесенная на антиферромагнитную подложку. Известно, что физические свойства пленки определяются свойствами ее поверхностей, т. е. граничными условиями. В [1] в качестве граничных рассматривались условия типа закрепления вектора намагниченности M на границе с антиферромагнетиком и свободного вектора M на границе с вакуумом.

В [2] было показано, что процесс перемагничивания такой магнитной системы носит пороговый характер, т. е. перемагничивание начинается с некоторого не равного нулю внешнего поля. Помимо этого в [2] была проведена аналогия между процессом перемагничивания и рассмотренным в работе [3] изгибом упругого стержня, защемленного с одного конца и свободного с другого, под действием внешней силы, приложенной к свободному концу. Также следует отметить работу [4], в которой исследовался процесс перемагничивания магнитомягкой пленки на магнитожесткой подложке с учетом одноосной анизотропии как аналогия изгиба стержня со сжатием.

В [5] граничное условие жесткого закрепления было заменено условием упругого закрепления магнитного момента путем введения эффективного промежуточного слоя на границе «ферромагнетик–антиферромагнетик». В более поздних работах (например, в [6]) рассматривалась двухслойная ферромагнитная система на антиферромагнитной подложке, слои которой жестко связаны между собой, как аналогия изгиба под действием внешней сосредоточенной нагрузки двухзвеньевого стержня,

жестко защемленного на одном конце и свободного на другом [7].

Однако до настоящего времени не было исследовано влияние немагнитной прослойки на распределение намагниченности и пороговые поля перемагничивания. Поэтому в данной статье будет рассматриваться двухслойная магнитомягкая система на магнитожесткой под-

ложке, но с присутствием между магнитными слоями немагнитной прослойки. Наличие последней требует постановки нового граничного условия.

Запишем потенциальную энергию ферромагнетика во внешнем магнитном поле H , следуя [8], в виде

F fM, M) =1 ^^M — + w (M) + fM2) - MH, (1) ( dxk ) 2 ,k dx,- dxk a’ ’ ' ’ где первое слагаемое представляет собой квадратичную форму, составленную из производных намагниченности по пространственным координатам; wa(M) – энергия магнитной анизотропии; f(M 2) – некоторая функция от M 2. Мы будем рассматривать изотропные ферромагнитные пленки, в которых неоднородность распределения намагниченности имеется только по толщине пленки. Поэтому второе слагаемое обращается в нуль, а первое преобра-

зуется к виду

1 f dM Y

- al-----I .

2 ( dz )

Ось z направлена перпендикулярно слоям. Третье слагаемое рассматривать не будем, так как при варьировании полной энергии оно дает нуль, поскольку длина вектора намагниченности считается неизменной. В результате энергию ферромагнитных слоев можно записать следующим образом:

^d 1 ^f 1

U = J 2 ai

d M ₁ dz

.2             )

I - M1H dz +

^d 1 ^{+ d}s ^{+ d} 2

+ J d1 + ds

f 1    f d M₂ Y

- a₂ 1I

2   ( dz )

)

- M ₂ H dz ,

где d 1 , d ₂ - толщины; M 1 , M 2 - намагниченности; a 1 , a ₂ -константы внутреннего обмена первого и второго слоев соответственно; d_s – толщина прослойки; H – внешнее магнитное поле.

Энергию межслойного взаимодействия представим в виде

a

U s =--^ M 1 M 2 , d_s

где a - постоянная межслойного взаимодействия. Коэффициент при произведении намагниченностей выбран

из тех соображений, что с увеличением толщины прослойки энергия взаимодействия должна убывать.

Таким образом, полная энергия магнитной системы составит

d i ( 1

U = j 2 ai

d M _i Y dz J

I MiH dz +

где z – нормированная на толщину слоя переменная (0 <  z <  1). Далее будем использовать обозначение С = ( a M ₂)/( dM ₁), которое характеризует жесткость связи слоев. При больших значениях C первое уравнение в (8) переходит в ф ₁ = ф ₂.

Помимо условий сшивки из (6) следуют два граничных условия:

d2 Г 1+ j 1

d 1

, d M₂ Y a ₂ 1 ² I

2 ( dz J

л

- M₂H dz -a² M.M

21 J        ^d s

. (4) d 1

2 d ф, „ a, M_x —¹ Зф, dz

= 0,

В пределах интегрирования величиной d_s пренебрегаем, так как считаем ее малой по сравнению с толщинами ферромагнитных слоев.

В данной задаче удобно перейти от проекций векторов к обобщенным координатам, которые представляет собой углы поворота векторов плотности намагниченности относительно оси x , направленной вдоль внешнего поля. Соответственно при полях ниже пороговых плотность намагниченности направлена против поля, поскольку мы рассматриваем процесс перемагничивания. Запишем выражение для полной энергии магнитной системы (4) в новых координатах:

2 d ф₂ „ a ₂ M ₂--- Зф ₂

= 0.

Будем считать, что магнитные моменты нижнего фер-

ромагнитного слоя жестко связаны с магнитными мо-

ментами подложки, поэтому угол ф ₁ на границе с подложкой будет оставаться неизменным, благодаря чему его вариация станет равной нулю. На границе с вакуумом магнитные моменты имеют свободу. Математичес-

ки это выразится в условиях следующего вида:

ф1к = 0,

U = Я 2 a M i ^{2 Г} ^

dz

,2                        I

I + M 1 H cos ф ₁ dz +

d ф ₂ dz

= 0.

d i + d 2

^d 2 ^f 1     iz2 f d ф:

+ j 2 a 2M2

d 1

-

dz

\2                  I

I

— I + M ₂ H cos ф ₂

dz -

a /        \

—M,M ₂ cos ( ф₂-ф] ) . ds

d 1

Исходя из условия минимума энергии в

состоянии

равновесия получаем выражение

5 U = a!M 2 dф1 Зф!

1 1dz1

d 1

dФ2 s

+ a2 M г —2 Зф2

2 2dz 2

d ₂

- d1

di f        , d2 ф.I

-J a, M ,²—^ + MH sin ф, 5ф, dz -

112             1                 11

01 dzJ

d2 Г       ,-jl a2M2

d i I

d 2ф?          ■ L

—— + M-H sin ф₂ Зф₂ dz +

dz2                    J

+ a ^s M 1 M 2 sin ( ф ₂ -ф 1 ) З ( ф 2 -ф 1 ) d_s

= 0.

d 1

Поскольку вариации 5ф ₁ и Зф ₂, входящие под знак интеграла, являются произвольными, то из (6) следует система независимых дифференциальных уравнений, определяющих распределение намагниченности в слоях:

„ d 2 ф1   тг ■ А a] M] —-1 + H sin ф] = 0, 1 1dz 21

Л z d ф2 , rr ■         А a2 M2 —2- + H sin ф2 = 0.

dz ²

Слагаемые, не входящие в интегралы, скомбинируем при одинаковых вариациях Зф , , где i = 1, 2. Если при этом учесть их независимость и произвольность, то получим следующие условия сшивки в точке d ₁:

a₁ d ф₁ _ a _s M ₂

■

d1dz a1 M2 d ф1

d s M 1

sin ( ф₂

ф1 ),

a₂ M 22 d ф₂

d ₁ dzd ₂ dz

Как частный случай рассмотрим систему, состоящую из одинаковых по толщине ферромагнитных слоев. Толщину каждого ферромагнитного слоя будем считать равной d . Уравнения, определяющие распределение направлений век-

тора намагниченности, запишутся следующим образом:

d2ф, + dz

Hd ² aM,

sin ф ,. = 0, i = 1, 2,

где z – нормированная на толщину слоя переменная. Решение этого уравнения хорошо известно (см. например,

[1; 2]) и записывается с помощью спецфункции sn( u , k ),

называемой эллиптическим синусом Якоби:

ф , ( z ) = 2arcsin k , sn

" I Hd² V a ,-M,

I!

, i = 1,2. (12)

Уравнение дополняется условиями сшивки на грани-

це сопряжения слоев

a, M, d^

^{1 1} dz

_{= aM} ^{d ф} 2 ^{( 0} ) La                      ,

²² dz

a1 dф7(i) = С sin(ф2 (0) - ф1 (1)) ddz

и условиями на границе с вакуумом и подложкой

[ dф—(1) = 0,

^ dz                          (13)

,ф1 (0) = 0.

Используемая при решении система координат приведена ниже (рис. 1). Из соображений удобства математических вычислений для каждого слоя введена собственная система координат. Спиралью отмечено наличие межслойного взаимодействия.

Применяя условия сшивки и граничные условия к

решениям, получим k 1 cn u 1 = yk2 cn u2,

■ p u ₁ k ₁ cn u ₁ = ( k ₂ sn u ₂ dn u ₁ - k ₁ sn u ₁ dn u ₂ ) x x ( dn u _i dn u ₂ + k ₁ k ₂ sn u ₂ sn u ₁ ) ,

п h где u = 4 ^h- > 2

, f п I a, h =          ;

c к 2 ) 4 d ²

u 2 = F 2 = к

( k, )-Л ML (Л ; ^{k 2}    4 y M 1 ^ hc

a, M 3

y =    ² —2-;

\] a₁ M 3

a, a, dM. р = — = — - ;

Cd a s dM ₂

cn(u, k), sn(u, k), dn(u, k) – соответственно косинус, синус и дельта-функция Якоби. Константа интегрирования F1 в этом случае равна нулю.

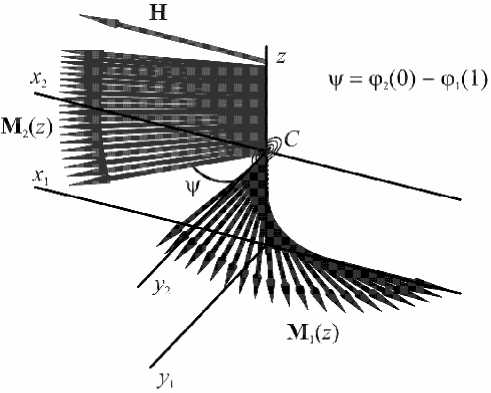
Рис. 1. Система координат

Из (14) можно определить пороговые поля перемаг- ничивания. Для этого воспользуемся тем фактом, что на пороге эллиптические модули k1 и k2 равны нулю, и тогда эллиптические функции перейдут в тригонометрические.

После преобразований получаем уравнение

П р 4

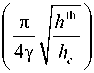
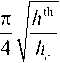
к

/

где h ^th = H ^th M – пороговое поле. Решая уравнение (15) относительно h th h c при разных значениях у и р , получаем зависимость, изображенную на рис. 2.

h ^th / h с

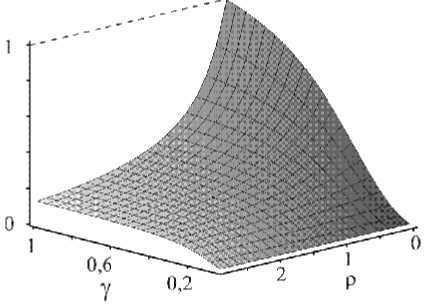
Рис. 2. Зависимость пороговых полей от у и р hth =

Уравнение (15) в предельном случае отсутствия прослойки ( d_s = 0) для двух одинаковых ферромагнитных слоев ( у = 1) дает известный результат

2 п ] a1 2 J 4 d2 ’ что соответствует пороговому полю одного ферромагнитного слоя толщины 2d.

В другом предельном случае, когда толщина прослой- ки велика и взаимодействие между слоями мало (р ^ ”), из второго уравнения (14) получаем п № cos        = 0,

4 hc что дает

, th f ^п I ^a i h =            .

k 2 J d ²

Этот результат соответствует пороговому полю одного ферромагнитного слоя толщины d . Таким образом, в случае отсутствия взаимодействия между слоями пороговое поле имеет только слой, сопряженный с подложкой.

Необходимо также исследовать поведение кривых перемагничивания. Рассмотрим частный случай двух одинаковых ферромагнитных слоев, разделенных немагнитной прослойкой. Варьировать будем только параметр р. Среднее значение проекции намагниченности на ось x можно определить по формуле mx = J mxdz = -J cos Ф dz ■

Производя интегрирование, получаем

1 mv = 1--x u1

xk E ( am [ u _{1 =} k ₁ ] , k ₁ ) - E ( am [ K ( k ₂ ) - u_v k ₂ ] , k ₂ ) + E ky , k ₂ JJ , (16) где am( u , k ) – амплитуда Якоби.

Полученные кривые перемагничивания (рис. 3) соответствуют следующим системам: магнитной системе, состоящей из одного ферромагнитного слоя толщины 2d, поскольку ds, а значит и параметр р, равны нулю (кривая 1); системам, включающим немагнитную прослойку разной толщины (кривые 2, 3), причем системе с более толстой прослойкой соответствует кривая, имеющая большее смещение в сторону низких внешних полей в начале про- цесса перемагничивания.

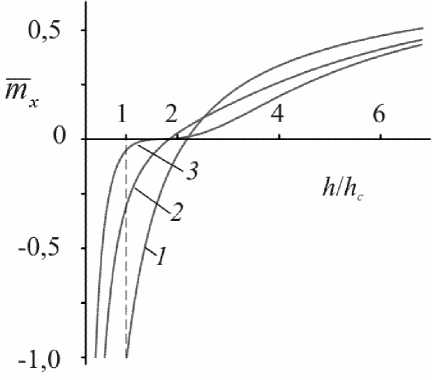
Рис. 3. Зависимость проекции средней намагниченности на ось х от внешнего поля при разных значениях параметра р: 1 - р = 0; 2 - р = 1,4; 3 - р = 2,8

На кривой 3 заметна пологость в районе нулевого значения проекции намагниченности. Это можно объяснить тем, что в рамках рассматриваемой модели в процессе перемагничивания нижнего слоя имеется конкуренция между влиянием обменной связи с магнитожесткой подложкой и обменного взаимодействия с верхним слоем. При определенном соотношении физических характеристик магнитомягких слоев и немагнитной прослойки на некотором интервале внешнего поля начинает преобладать влияние обменной связи подложки, благодаря чему намагниченность нижнего слоя может вернуться в начальное положение, т. е. она будет стремиться ориентироваться против поля. При дальнейшем увеличении внешнего поля последнее совместно с обменным взаимодействием преодолевает влияние подложки, и процесс перемагничивания в нижнем слое продолжается.

Т аким образом, было проведено исследование влияния немагнитной прослойки в системе «ферромагне-тик–прослойка–ферромагнетик–антиферромагнетик» на величину порогового поля начала перемагничивания и построены кривые перемагничивания при разных значениях введенного эффективного параметра ρ , характеризующего межслойное обменное взаимодействие.