Продольное сопротивление одноцепной лэп с двумя грозозащитными тросами в задаче дистанционного ОМП

Решение таких задач, как дистанционное определение места повреждения при однофазных коротких замыканиях в сети с эффективно заземленной нейтралью, требует высокой точности результатов расчета параметров аварийного режима. Во многом она будет зависеть от используемой в расчете схемы замещения линий электропередачи, которая должна учитывать не только сопротивления проводящих элементов, но также их электромагнитное и электростатическое взаимодействие.

Одним из наиболее простых способов представления в расчете ЛЭП является использование справочных данных об их удельных сопротивлениях и емкостной проводимости. Однако такой способ не позволяет учесть действительные расстояния между проводящими элементами и не учитывает возможность использования проводов сечением более 300 мм2 в сети напряжением 110 кВ. Такая ситуация характерна, например, для систем электроснабжения крупных промышленных предприятий, характеризующихся высокой плотностью нагрузки. Более точные результаты дает использование схемы замещения ЛЭП, приведенной в руководящих указаниях по расчету токов КЗ для релейной защиты [1]. Приведенные в руководящих указаниях схемы замещения подразумевают использование для расчета параметров режима мето-

да симметричных составляющих, а значит, не могут учесть несимметрию линии, вызванную, например, несимметричным расположением фазных проводов друг относительно друга и относительно грозозащитного троса.

Широко применяется моделирование электроустановок в среде MATLAB Simulink. Так, данный инструмент может быть использован для описания процессов, протекающих при однофазных замыканиях на землю в сети 6–35 кВ [2], а также для моделирования режимов работы длинных ЛЭП высокого и сверхвысокого напряжения [3–6]. Однако в MATLAB Simulink затруднительно смоделировать режимы работы системы промышленного электроснабжения с несколькими источниками электрической энергии (внешняя энергосистема и собственные электростанции), уровнями напряжения от 0,4 до 500 кВ и числом элементов более 10 000. Связано это в первую очередь с большим временем счета и высокими требованиями производительности компьютера.

Одним из наиболее удобных методов расчета параметров режима однофазного короткого замыкания является метод симметричных составляющих [7]. Применение данного метода к моделированию режимов аварийной несимметрии в условиях систем промышленного электроснабжения с собственными электростанциями рассмотрено в [8].

Однако данный метод не позволяет учесть возможную несимметрию элементов схемы. Такая ситуация может возникнуть, например, при работе двухцепной ЛЭП с одной отключенной цепью. При наличии у такой ЛЭП грозозащитных тросов возникает несимметрия сопротивлений линии, обусловленная электромагнитным взаимодействием ее проводящих элементов. Такую несимметрию необходимо учитывать при выполнении расчетов с целью дистанционного определения места повреждения (ОМП).

Для учета несимметрии линии электропередачи по фазам, обусловленной расположением проводов на опоре, а также для учета электромагнитного и электростатического взаимодействия ее проводящих элементов целесообразно использовать метод фазных координат [9, 10]. Данный метод широко применяется для решения задач расчета режимов электрических сетей, содержащих несимметричные элементы. Например таких, как системы электроснабжения тяговых сетей. В работах [11, 12] авторы привели описание математической модели энергосистемы, в том числе модели многофазной ЛЭП, предназначенной для расчета и анализа параметров симметричных и несимметричных режимов. Однако такая модель электрической сети подразумевает, что все ее элементы представлены трехфазной схемой замещения. Такой подход может быть неудобен в схемах с большим числом элементов ввиду сложности подготовки исходных данных. Авторы [13] использовали данный метод для исследования влияния наличия грозозащитного троса, изменения частоты в сети и поверхностного эффекта на сопротивление ЛЭП. Также метод фазных координат используется для определения индуктивности и емкости многоцепных ЛЭП [14], линий с изолированными проводниками [15] и ЛЭП разных уровней напряжения на одной опоре [16].

Несимметричное распределение тока также может быть обусловлено взаимоиндуктивным влиянием близко расположенных ЛЭП [17]. Авторы [18] предложили метод «виртуальной» линии, который позволяет скорректировать ток нулевой последовательности с учетом взаимоиндуктивного влияния соседних ЛЭП. Для расчета сопротивления ЛЭП в работе [19] использован метод конечных элементов. Разработанная модель позволяет оценить индуктивность и емкость ЛЭП с учетом конфигурации опоры, а также наличия расщепления фазного провода.

Из-за особенностей систем промышленного электроснабжения актуальной является задача учета не-симметрии ЛЭП без усложнения схемы замещения в целом.

Продольное сопротивление одноцепной ЛЭП с двумя грозозащитными тросами

Для моделирования одноцепной ЛЭП с двумя грозозащитными тросами в работе использован метод фазных координат. В соответствии с ним сопротивление проводящих элементов и их взаимоиндукции может быть представлено в виде матрицы 5×5:

ZAA ZAB ■___ ZAC ZAT1 ZAT2 ZAB ZBB ZBC ZB T1 ZB T2 Z^ ■ ZAC ZBC ■ ZCC ZCT 1 ZC T2 ZATi ZB T1 ZC T1 7 ZT1T1 ZT1T2 \Z^A T2 ZB T2 ZC T2 7 ZT1T2 ZT2T2/ где ZAA, ZBB, ZCC – собственные сопротивления фаз ЛЭП; ZT1T1, ZT2T2 – собственные сопротивления грозозащитных тросов; остальные элементы – сопротивления взаимоиндукции между фазами, фазой и тросом, а также грозозащитными тросами.

Собственные сопротивления фаз либо тросов Z _L , а также сопротивления взаимоиндукции Z _M определяются по известным выражениям из [1]:

Z L ■ r 0 + r з + j0,145lg ( 0^ ) ; Z m ■ r 3 + j0,145lg ( D ),                                           (2)

где r ₀ – удельное активное сопротивление провода либо троса, Ом/км; r _з – сопротивление, учитывающее потери активной мощности в земле при протекании в ней тока (принимается равным 0,05 Ом/км); D _з – глубина залегания обратного провода (935 м); ρ _п – радиус провода, м; D _п – расстояние между проводниками фаз либо тросами, м.

Для того чтобы использовать математическую модель ЛЭП в фазных координатах совместно со схемой замещения электрической сети в симметричных составляющих, матрицу Z необходимо разделить на четыре части:

( ^Z AA

Z п    I ^Z AB

\ZAC

■

Z

т пт

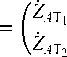
Z^BA Z^BB

^Z BC

^Z B T 1

^Z B T ₂

Z CA ^Z CB

Z CC

\        /^ZA T   ^ZA T,\

I; Z пт = I ^Z B T 1    ^Z B T ₂ I ^;

Z C T 1   Z C T 2

;

Z C T 1

^Z C T ₂

)■ Z = ( Z

T 1 T 1

T 1 T 2

7 Z T 1 T 2

7 Z T 2 T 2

).

Электроэнергетика

Это позволяет преобразовать матрицу сопротивлений одноцепной ЛЭП с двумя грозозащитными тросами (1) к матрице размерностью 3×3:

a

а

—1 1

^Z п(т) = Zn ^{— Z} пт ^Z т Zrn = I ²

\2

Z AA (т)	7 ZAB> (т)	7 Z AC (т)
Z AB (т)	Z BB (т)	7 Z BC (т)
,ZAC (т)	7 Z BC (т)	7 Z CC (т)

)

TI                   W                Z^SX                                         Z                   Az      X

В полученной матрице (3) диагональные элементы (на примере Z _AA (_т) ):

А

А

7   —7 A

Z AA (т) Z AA ⁺

Z Т2Т2 Z A Т1 + Z Т1Т1 Z A Т1 – 2 Z Т1Т2 Z A Т1 Z A Т2

А 1Т2 ^— Z Т1Т1 Z Т2Т2

.

TT

Недиагональные элементы матрицы (3) на примере Z _AB (т) :

А

А

7   —7 A

Z AB (т) Z AB ⁺

Z A Т1 Z B Т1 Z Т2Т2 + Z A Т2 Z B Т2 Z Т1Т1 ^— Z Т1Т2 ( Z A Т1 Z B Т2 + Z A Т2 Z B Т1 )

Z r 1Т2 ^— Z Т1Т1 Z Т2Т2

.

Для преобразования Z _п(_т) в симметричные составляющие используется следующее выражение:

/ Z 1

Z S (т) = 3 S ^-1 Z п(т) s = 3 Z 21

\ Z 01

Z 12

■ z2

^Z 02

ZA

Z 20   ,

ZJ

где s – матрица фазового поворота, содержащая оператор a = – ¹ + j ^{√ 3} :

s = a ² a 1 .

a a 2    1

Преобразование в соответствии с (4) позволяет вычислить сопротивления прямой, обратной и нулевой последовательности одноцепной ЛЭП с двумя грозозащитными тросами. Данные величины будут нальными элементами полученной матрицы. Получим:

диаго-

– сопротивление прямой (обратной) последовательности:

А

A

=

Z T 1^T2^— Z ^T1T1 Z ^T2^T2

;

A = 7, ZA т +7„„72 т +7^72 т

AA T ₁ T ₂      BB T ₁ T ₂      CC T ₁ T ₂

А- А

А

А- А

А

А- А

А

– Z _AA Z _{T 1 T 1} Z _{T 2 T 2} – Z _BB Z _{T 1 T 1} Z _{T 2 T 2} – Z _CC Z _{T 1 T 1} Z _{T 2 T 2} +

^{+ Z} A T 1 ^Z T ₂ T ₂

+ Z _{A T 2} Z _{T 1 T 2}

+ Z B T 1 Z T 2 T 2

^{+ Z} C T ₂ ^Z T 1 T 1

• 2- А- А

• ■         ■         А

• ■         ■         А

• ■         ■ А

• ■         ■         А

• – 2 Z _{A T 1} Z _{A T 2} Z _{T 1 T 2} + Z _{A T 1} Z _{B T 2} Z _{T 1 T 2} + Z _{A T 1} Z _{C T 2} Z _{T 1 T 2} – Z _{A T 1} Z _{B T 1} Z _{T 2 T 2} – Z _{A T 1} Z _{C T 1} Z _{T 2 T 2} +

• ■         ■ А

• ■        ■        Д

А» А» А

А» А» А

— 7 7 7   — 7 7 7     7 7 7     7 7 7 A

+ Z _{A T 2} Z _{B T 1} Z _{T 1 T 2} + Z _{A T 2} Z _{C T 1} Z _{T 1 T 2} – Z _{A T 2} Z _{B T 2} Z _{T 1 T 1} – Z _{A T 2} Z _{C T 2} Z _{T 1 T 1} +

А» А» Д

• ■        ■        А

• ■        ■ д

– 2 Z _{B T 1} Z _{B T 2} Z _{T 1 T 2} + Z _{B T 1} Z _{C T 2} Z _{T 1 T 2} – Z _{B T 1} Z _{C T 1} Z _{T 2 T 2}

⁺ Z C T 1 ^Z T ₂ T ₂ ^— 2 ^Z C T 1 ^Z C T ₂ ^Z T 1 T ₂ ⁺

А» А

А

А» А

А

А» А

А

+ Z AB Z T 1 T 1 Z T 2 T 2 + Z AC Z T 1 T 1 Z T 2 T 2 + Z BC Z T 1 T 1 Z T 2 T 2

– Z _AB Z _{T 1 T 2} – Z _AC Z _{T 1 T 2} – Z _BC Z _{T 1 T 2} ;

– сопротивление нулевой последовательности

А

B

Z =

Z T 1T₂^{- Z} T1T1 ^Z T₂T₂

;

2A     Z.,,,72      Zr-rZTZ        Z.,,,72  +7^72  +7„^72                   72,-r

^U   ^AA ^ZyT1 T 2    BRBT T 1 T 2    CCC ^ZyT1 T 2    ^ \Ab AB^ T 1 T 2 ^AC ^ZyT1 T 2 ^BCT T 1 T 2 /    ^TT 1^Z" T 2 T 2    ^T T 2^Zy T 1 T 1 ⁺

0                 0                 0                 0

+ Z _{B T 1} Z _{T 2 T 2} + Z _{B T 2} Z _{T 1 T 1} + Z _{C T 1} Z _{T 2 T 2} + Z _{C T 2} Z _{T 1 T 1}

А» А

А

А» А

А

⁺ 2⁽ Z. a T 1 Z. b T 1 ZL T ₂ T 2 ^{- 2 ( Z} a T 1 2^ a t₂ 2^ T 1 T 2

■                 ■                 ■

А» А» А

А» А

А

– Z _AA Z _T1T1 Z _T2T2 – Z _BB Z _T1T1 Z _T2T2 ■         ■         A.                ■         ■         A.

– Z _CC Z _{T 1 T 1} Z _{T 2 T 2} +

— 7  7  7   — 7  7  7   — 7  7  7   — 7  7  7

+ Z A T 2 Z B T 2 Z T 1 T 2 + Z A T 1 Z C T 1 Z T 2 T 2 + Z A T 2 Z C T 2 Z T 1 T 1 + Z B T 1 Z C T 1 Z T 2 T 2

А- А

А

• ■         ■         А

• ■         ■         А

А- А

А

^{+ Z} B T ₂ ^Z C T ₂ ^Z T 1 T 1 ^У ■                 ■                 ■

—

+ Z AB Z T 1 T 1 Z T 2 T 2 + Z A T 1 Z B T 2 Z T 1 T 2 + Z A T 2 Z B T 1 Z T 1 T 2 + Z AC Z T 1 T 1 Z T 2 T 2 + Z A T 1 Z C T 2 Z T 1 T 2 +

2- А- А

А- А

А

А- А- А

• ■         ■         А

+ Z A T 2 Z C T 1 Z T 1 T 2 + Z B T 1 Z B T 2 Z T 1 T 2 + Z BC Z T 1 T 1 Z T 2 T 2 + Z B T 1 Z C T 2 Z T 1 T 2 + Z B T 2 Z C T 1 Z T 1 T 2

+ Z C T 1 ^Z C T ₂ Z T 1 T 2 У

Полученные в данной работе математические модели ЛЭП позволяют составить комбинированную схему замещения, в которой ЛЭП высокого напряжения представлены в фазных координатах, а остальные элементы сети – в симметричных составляющих. Это значительно упрощает расчет параметров несимметричного режима и подготовку данных при составлении расчетной схемы. При этом обеспечивается возможность учета несимметрии линий электропередачи по фазам.

Расчет продольного сопротивления с использованием полученной схемы замещения

Для оценки полученных результатов в работе представлен расчет удельного продольного сопротивления одноцепной ЛЭП с двумя грозозащитными тросами. Для расчета принята опора типа ПП220-2/40 с проводами АС-300 и тросами ТК-9,1. Одна из цепей ЛЭП отключена, поэтому в расчете рассматриваем данную линию как одноцепную с двумя грозозащитными тросами.

В паспорте опоры указаны расстояния от стойки опоры до каждой фазы и троса (на рисунке обозначены буквой L ). На основе этих данных были рассчитаны расстояния между проводящими элементами. На рисунке показаны условные обозначения данных расстояний на примере фазы A . Результаты данного расчета приведены в табл. 1. В табл. 2 приведены параметры провода и троса.

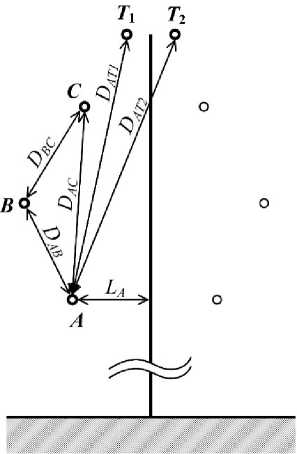
Таблица 1

Параметры опоры

Фаза	Расстояние, м					Расстояние от стойки опоры, м
	A	B	C	T 1	T 2
A	–	9,341	18	25,298	24,187	5,5
B	9,341	–	9,487	18,31	15,977	8
C	18,007	9,487	–	9,605	6,5	5
Т 1	25,298	18,31	9,605	–	5	2,5
Т 2	24,187	15,977	6,5	5	–	2,5

Параметры провода и троса

Таблица 2

Марка	Активное сопротивление, Ом/км	ρ п , см
АС-300	0,098	12
ТК-9,1	3,25	4,55

Расстояния между фазными проводами и тросами на опоре

Используя формулы (2) и данные табл. 1 и 2, составили матрицу сопротивлений рассматриваемой одноцепной ЛЭП с двумя тросами по (1), Ом/км:

■

Z =

/0,148 + j 0,568

⎛ 0,05 + j 0,29 ⎜ 0,05 + j 0,249

0,05 + j 0,227

⎝ 0,05 + j 0,23

0,05 + j 0,29    0,05 + j 0,249 0,05 + j 0,227 0,05 + j 0,23 \

0,148 + j 0,568   0,05 + j 0,289  0,05 + j 0,248  0,05 + j 0,256⎞

0,05 + j 0,289   0,148 + j 0,568  0,05 + j 0,288  0,05 + j 0,313⎟

0,05 + j 0,248   0,05 + j 0,288   3,3 + j 0,629  0,05 + j 0,329

0,05 + j 0,256   0,05 + j 0,313   0,05 + j 0,329   3,3 + j 0,629 ⎠

Из полученной матрицы видно, что удельные сопротивления взаимоиндукции отличаются друг от друга ввиду несимметричного расположения проводящих элементов на опоре. Так, разность между удельными сопротивлениями взаимоиндукции фазных проводов достигает 14,1 %, фазных проводов и первого троса – 21,2 %, фазных проводов и второго троса – 26,5 %.

Пользуясь формулами (5) и (6), выполнили преобразование Z в симметричные составляющие:

Z ̇ ₁(₂) = 0,099 + j 0,291 Ом/км;

Z ̇ ₀ = 0,344 + j 1,045 Ом/км.

Электроэнергетика

Для оценки полученных результатов и сравнения их с сопротивлениями, полученными с учетом среднегеометрических расстояний, был выполнен расчет Z 1(₂)._РУ и Z 0._РУ по [1]. Для рассматриваемой ЛЭП среднегеометрическое расстояние между фазными проводниками составляет D _ср = 11,684 м, а между проводами и тросами D пт.э = 14,952 м.

При таких параметрах ЛЭП, а также характеристиках провода и троса, приведенных в табл. 2, получим

Z 1 (2).ру = 0,098 + j 0,292 Ом/км;

Z ₀._РУ = 0,344 + j 1,106 Ом/км.

Видно, что сопротивление нулевой последовательности, определенное на основе среднегеометрических параметров ЛЭП, имеет индуктивную составляющую на 5 % больше, чем сопротивление, определенное на основе метода фазных координат.

Заключение

В работе представлена комбинированная схема замещения одноцепной линии электропередачи с двумя грозозащитными тросами, предназначенная для совместного использования методов фазных координат и симметричных составляющих для выполнения расчетов параметров несимметричных аварийных режимов. Данную модель предлагается использовать для расчета и анализа несимметричных режимов в условиях систем про-

мышленного электроснабжения, которые характеризуются преобладанием разомкнутых участков сети над замкнутыми, наличием нескольких ступеней напряжения, собственной генерации, высокой плотностью нагрузки и сравнительно короткими ЛЭП напряжением 110 и 220 кВ [20]. Все эти особенности затрудняют использование методов расчета режима, предназначенных для сетей энергосистемы. Представленная модель ЛЭП может быть использована для расчета параметров режима с использованием сочетания методов последовательного эквивалентирования, симметричных составляющих и фазных координат. При этом метод последовательного эквивалентирования используется для определения параметров предшествующего установившегося режима, метод симметричных составляющих – для расчета параметров несимметричного режима и оставления схемы замещения, а метод фазных координат – для моделирования ЛЭП. Такой подход позволяет одновременно упростить расчет режима и учесть возможную несимметрию линий электропередачи. Как показали результаты моделирования одноцепной ЛЭП с двумя грозотросами, удельное сопротивление нулевой последовательности, определенное с использованием комбинированной схемы замещения, оказалось на 5 % меньше аналогичного сопротивления, определенного по руководящим указаниям [1] с использованием метода симметричных составляющих.