Продольные резонансные колебания вязкоупругого каната грузоподъёмной установки
Автор: Анисимов Валерий Николаевич
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Информатика, вычислительная техника и управление
Статья в выпуске: 4-1 т.18, 2016 года.
Бесплатный доступ
В статье исследуются резонансные свойства каната грузоподъёмной установки. Объект исследования относится к широкому кругу колеблющихся одномерных объектов переменной длины. Для описания колебаний использована классическая математическая модель. При решении использовался метод Канторовича-Галёркина. В отличии от асимптотических методов решение имеет модовую структуру, что позволяет анализировать резонансные свойства каната. Пренебрежение малыми величинами позволило получить сравнительно простое выражение для амплитуды резонансных колебаний. С помощью полученного выражения проанализированы явления установившегося и прохождения через резонанс. В отличии от большинства исследований в данной области в статье приведены количественные характеристики резонансных свойств. Результаты анализа представлены в виде графиков. Решение произведено в безразмерных переменных, что позволяет использовать полученные количественные результаты для анализа колебаний технических объектов.
Колебания объектов с движущимися границами, краевые задачи, математические модели, резонансные свойства
Короткий адрес: https://sciup.org/148204643
IDR: 148204643 | УДК: 534.11
Текст научной статьи Продольные резонансные колебания вязкоупругого каната грузоподъёмной установки
Рис. 1. Схема грузоподъемной установки в недеформированном состоянии; ν(t) – окружная скорость барабана; m – масса груза.
Обозначим Z ( x, t ) – смещение точки каната с координатой x в момент времени t . Ось x связана с неподвижной системой координат (точкой подвеса барабана). В начальный момент времени точки недеформированного каната связаны с точками оси x . На рис. 1 недеформированный канат изображён в начальный момент времени. Между l ( t ) и ν( t ) имеет место следующее соотношение:
r«l + Zx(l(t)±O,t)) = -v(t). (1)
При спуске используется значение Zx(l(t) + 0, t) , т.е. выше точки подвеса. При подъёме Zx(l(t)-0,t) , т.е. ниже. После пренебрежения Zx(l(t) ± 0, t) по сравнению с единицей получим:
Z4O = -v(t) .
Математическая модель, описывающая продольные колебания каната, имеет вид [2]:
pZtt(x, t) - EZxx(x, t) - pZxxt(x, t) + pg = 0;
mZtt(0, t) — ESZx(0, t) — gSZxt(0, t) + mg = 0;
ZtUto.t) = WY п.тд(х-1Щ pg
Введём новую функцию
Z(x, t) = u(x, t) + ^ (% - Z(0)) + ^ (x2 - Z(0)2).
Здесь функция
(^(x-/(0))+^|(%2-/(0)2)) характеризует первоначальные деформации каната, компенсирующие вес груза и троса.
В результате задача (2) примет вид:
putt(x, t) - Euxx(x, t) - guxxt(x, t) = 0; (3) mutt(0,t) — ESux(0, t) — nSuxt(0, t) = 0; (4)
ut(l(t), t) = v(t); (5)
u(_x, 0) = 0 ; ut(x, 0) = v(0).
Выразим UtOto-Oчерез полную производную du(l(tY t)
MKf), t) =---—--ux(l(t\ ty(t).
at
С учётом равенства (1) и интегрирования по dt граничное условие (5) примет вид
u(l(t\t) = J^vCcM = F(t). (6)
Статья посвящена изучению вынужденных колебаний объекта, поэтому в дальнейшем начальные условия не рассматриваются. Примем i(t) = -vot + 1№ , где v0 средняя окружная скорость барабана в период наблюдения резонансного явления. Для F ( t ) возьмём следующее выражение:
F(t) = vot + Asin w(t), (7)
где Asin ω( t ) характеризует слабые возмущения гармонического характера, связанные с отклонением формы барабана от окружности, а также с вибрациями барабана.
Введём безразмерные переменные:
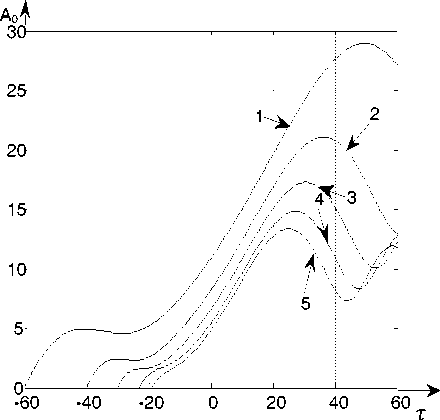
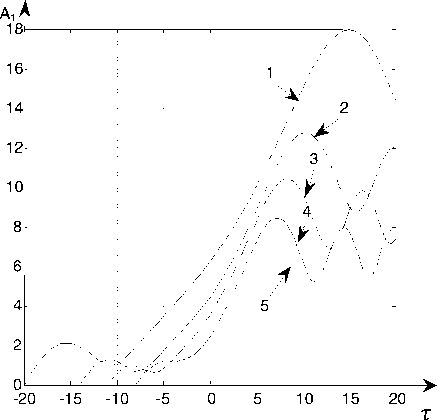
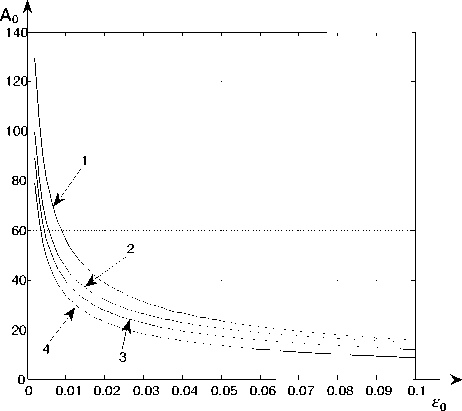
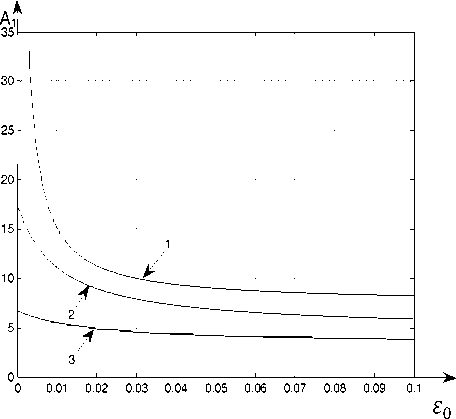
^ = "i7m’ T = 77(^t’ "ГТ^КС = L(eot) = 1 + гот; £o Vq a " Здесь a – скорость распространения продольных волн. Малый параметр ε0 характеризует медленность движения границы по сравнению со скоростью волн. В результате задача (3)-(5) с учётом (6),(7) примет следующий вид: итАУ^ - U^.t^ - £1U^>^ = 0; (8) Ftt(0,t) ~^U^Q,t) + £1^t(0,t) - 0; (9) U(L(eot), t) = eot + BsinW(r'), (10) где n A x /Z(0) A £i = ——; M = — ; В = —- ; Ж (т) = w (— т) . 1 арЦоУ pSl(0) Z(0) v J V a ) . Малый параметр ε1 характеризует малость сил внутреннего трения по сравнению с упругими силами. Параметр M представляет собой отношение массы груза к массе каната. Выразим Uττ(ξ,τ) из (8) и подставим в (9). В результате граничное условие (9) примет следующий вид: U^(0, r) - i^(0, r) + £1(u„T(.O,^-^ЩА0,t)) = 0. Для выполнения граничного условия (11) достаточно чтобы U^(0,t)-^U?(0,t) = 0. (12) Для получения однородных граничных условий введем новую функцию: u(^, t) = V(^, t) + Я(f, t) - E0T, f2 + 2Mf где H^, t) = ——-— ---—-BsinW(jy 5 L2(e0t) + 2ML(eot) В результате задача (8),(10),(12) примет следующий вид: Vtt(^,t) -V^.t) - £1V№(^.t) = = -HTT^,^ + H^,t^ + г^^С^т).(13) ^(0,т) -^f(0,T) = 0; /(L(eot),t) = 0. (14) РЕШЕНИЕ ЗАДАЧИ Решение будем производить с точностью до членов порядка малости ε2 , т.е. членами, содержащими ε02 и ε0ε1 , будем пренебрегать. Для решения задачи (13), (14) будем использовать метод Канторовича-Галеркина [5]. Решение будем искать в виде v^,^ = ^tiv^,^, (15) где Цг(С^) = <рп(т)Хп(^гот). (16) В качестве Xn(ξ,ε0τ) возьмём следующие функции: Хп^,Е0т) = sin (wn(£0r)(^ - L(eot))) ■ (17) Данные функции удовлетворяют граничным условиям (14), если ωn(ε0τ) удовлетворяет уравнению ton^oT)tg(ton(£oT)L(soT)) =^. (18) Заметим, что функции (17) при неподвижной границе (ε0 = 0) являются собственными формами колебаний. В этом случае метод Канторовича-Га-леркина дает точное решение. При увеличении б0 точность уменьшается. Статья посвящена анализу резонансных явлений наблюдаемых на одной из собственных частот. Амплитуда колебаний на резонансной частоте многократно увеличивается. Амплитуда колебаний на нерезонансных частотах соизмерима с возмущающими воздействиями. При этом нерезонансными членами ряда (15) можно пренебречь и рассматривать решение только на одной резонансной моде. Функции, определяемые выражением (17), не являются ортогональными, но ортогональными являются их производные по £, т.е. . Проинтегрируем уравнение (13) по си подставим в него Vn(^,т), определяемое выражением (16). Согласно методу Канторовича-Галеркина, умножим полученное уравнение на и проинтегрируем по d^ в интервале от нуля до L(т). В результате с точностью до величин порядка б2 получим следующее уравнение для определения функций фп(т): №) + 2Ап(т)<р^(т) + ш2(е0т)<Рп(т) = где 1 l'(£ot) L'(еот) 2А°^ ML(eot) £12М £° + L(eot) £° ’ 7ГП 1 "п(£°т) ~ М^ + ^М; 51Г1((Оп(е0т)£(е0т)) « ---— . ппМ Данные значения имеют погрешность менее 5% при M>3. При получении коэффициентов (20) отброшены члены, которые имеют значимость менее 5% по сравнению с другими членами. Введём в уравнение (19) новую функцию: где ) . В результате уравнение (21) с точностью до величин порядка б2 примет вид: , (22) где РпЧ) . Функции с учётом (20) имеют вид: С0(т) = exp I--(! + —-)1п(£(еот))+—) Сп(т) — exp £17Г2П2Т 2L(eot) Два линейно независимых решения однородного уравнения соответствующего уравнению (22) c точностью до величин порядка б2 имеют вид: Уп1 W = атг(Еот) cos(w„(t)) л2п2 2Ал(т) = Et ЕЧад В L'(EqT) , L(eot) ’ Уп2М = a«(£o^) sin((w„r)) где w„(t) - ^тгС^О^)^^ ^ ^пС^О^-) — PqCO =--7---Г77---7 Wo(wL(eot) (^'(т))2 7шп(еот) После интегрирования получим Еч^У+гм Wo(t) =— -^Д >wnM = — 1п(£(еот)) + —Т—. £цх М Ео клМ 2В Р М = ------- J а^тМ^ (Ж(т))2 + L2(e0t) + 2М тГ(т) ШП(£ОТ) Решение уравнения (21) при нулевых начальных условиях имеет вид: г X f ^nto cosfwn(c)) sinflV(c)) ■Pn(r) = —Сп(т)а„(гот) sin(ivn(r)) ------ -----^ dS - f O„M sin(wn (?))sin(lV(?)) -Cn(T)a„(£or)cos(wn(T)) ----- -----dS. J ^nx^O^J^nV^oP) При получении коэффициентов(20) использованы следующие приближённые значения частот уравнения (18) и их sin: 1 шо(еот) « , ^ ^ ; 7М£(еот) После пренебрежения нерезонансными членами и с учётом (21) получим следующее выражение для амплитуды вынужденных колебаний на n-ной динамической моде: ЛпИ = ^2Sn(T) = 51п(ш0(е0т)£(е0т)) = E„(T)((j Fn«) cos( n«))d<)2 + +(j ^n«) sin(On«))d<)2). Величина An(т) показывает во сколько раз амплитуда колебаний Bn(t) превосходит интенсивность внешнего возмущения B. Функции, входящие в выражение (24), имеют вид: Еп(т) = -(Сп(т)а^Еот)У; ------------- ; ^п (^ ) ^п («О ^) Фп«) = МО - М) ■ АНАЛИЗ РЕШЕНИЯ С помощью выражения (24) были проанализированы резонансные свойства объекта. Установившийся резонанс наблюдается, если . Если принять функцию медленного времени равной единице, то изменение амплитуды колебаний с учётом (23) будет описываться следующим выражением: Явление прохождения через резонанс наблюдается при внешнем возмущении постоянной частоты W(t) = Qt. На рисунках, приведённых ниже, представлены количественные результаты прохождения через резонанс. Возмущающая частота Q подбиралась таким образом, чтобы наилучшие условия для увеличения амплитуды наблюдались при т = 0. На рис. 2 и 3 показано как изменяется амплитуда A0(t) и A 1(т) в резонансной области при значении параметра M равном 5. Кривые 1, 2, 3, 4 и 5 получены для б0 соответственно равных 0.01, 0.02,0.03,0.04 и 0.05 .Собственная частота ю0(б0 т) обратно пропорциональна арЛе^т^ , а ю1(Б0т) обратно пропорциональна L(б0 т) , поэтому на нулевой собственной частоте прохождение через резонанс происходит медленнее, чем на первой. На рис. 4 и 5 показано, как изменяется амплитуда колебаний A0(t) и A 1(т) в зависимости от скорости изменения длины канатаБ0. На рис. 4 кривые 1, 2, 3 и 4 получены для значений M соответственно равных 50, 20, 10 и 5. Параметр вязкоупругости б0 слабо влияет на A0(t), т.к. при колебаниях на нулевой частоте основная часть энергии колебаний связана с колебанием груза, а малые демпфирующие силы действуют в канате. При колебаниях на первой и последующих частотах основная часть энергии колебаний связана с колебанием точек каната при этом параметр M, характеризующий массу груза, слабо влияет на амплитуду, а демпфирующие силы оказывают на амплитуду существенное влияние. На рис. 5 кривые 1,2 и 3 получены для значений б0 соответственно равных 0, 0.01 и 0.05. ЗАКЛЮЧЕНИЕ Таким образом, в отличии от асимптотических методов, использование метода Канторови-ча-Галёркина позволило для изучения колебаний получить решение, имеющее модовую структуру. Это актуально при анализе резонансных свойства каната. Пренебрежение малыми величинами позволило получить сравнительно простое выражение для амплитуды резонансных колебаний, что упрощает анализ резонансных свойств объекта. Рис. 2. Изменение амплитуды A0 в резонансной области Рис. 3. Изменение амплитуды A1 в резонансной области Рис. 4. Зависимость амплитуды A0 от скорости движения границы Рис. 5.Зависимость амплитуды A0 от скорости движения границы В отличие от большинства исследований в данной области в статье приведены количественные характеристики резонансных свойств. Результаты анализа представлены в виде графиков. Решение произведено в безразмерных переменных, что позволяет использовать полученные количественные результаты для анализа колебаний технических объектов.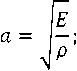
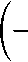
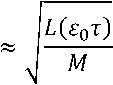
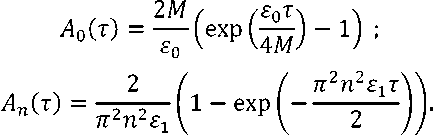
Список литературы Продольные резонансные колебания вязкоупругого каната грузоподъёмной установки
- Cамарин Ю.П., Анисимов В.Н. Вынужденные поперечные колебания гибкого звена при разгоне//Изв. Вузов. Машиностроение, 1986. № 12. С. 17-21.
- Горошко О.А., Савин Г. Н. Введение в механику деформируемых одномерных тел переменной длины. Киев: Наукова думка, 1971. 270 с.
- Лежнева А.А. Изгибные колебания балки переменной длины//Изв. АН СССР. Механика твердого тела, 1970. № 1. С. 159-161.
- Весницкий А.И. Волны в системах с движущимися границами. М.: Физматлит, 2001.320 с.
- Анисимов В. Н., Литвинов В. Л. Исследование резонансных свойств механических объектов при помощи метода Канторовича-Галёркина//Вестн. Сам. гос. техн. ун-та. Сер. Физ.-мат. науки. 2009. № 1(18). С. 149-158.
- Анисимов В. Н., Литвинов В. Л., Корпен И. В. Об одном методе получения точного решения волнового уравнения, описывающего колебания систем с движущимися границами//Вестн. Сам. гос. техн. унта. Сер. Физ.-мат. науки. 2012. № 3(28). С. 145-151.
- Динг Ху, Чен Ли-Квун Методы Галеркина для собственных частот движущейся в осевом направлении балки//Общие вопросы механики. Общая механика. 2011. № 2.
- Котера Тадаши. Вибрация струны с изменяющейся во времени длиной//Бюллетень Японского общества механической инженерии. 1978. Т. 21. № 162. С. 1677-1684.
- Жу В.Д., Женг Н.А. Точная реакция поступательно движущейся струны с произвольно меняющейся длиной при внешнем возбуждении общего вида//Общие вопросы механики. Общая механика. 2010. № 4.
- Лей Х. Влияние резких изменений жесткости основания железнодорожного полотна на его вибрацию при движущейся нагрузке//Общие вопросы механики. Общая механика. 2010. № 3.
- Сахебкар С.М., Гхазави М.Р., Кхадем С.Е., Гхаёш М.Х. Анализ нелинейной вибрации движущейся в осевом направлении бурильной колонны с зависящими от времени осевой нагрузкой и осевой скоростью в наклонной скважине//Общие вопросы механики. Общая механика. 2011. №7.
- Жу В.Д., Чен Й. Теоретическое и экспериментальное исследование динамики и управления каната лифта//Общие вопросы механики. Общая механика. 2006. № 9.
- Анисимов В.Н., Литвинов В.Л., Корпен И.В. Постановка задачи о колебаниях балки с движущейся подпружиненной опорой//Вестн. Сам.гос. техн. унта. Сер. Технические науки. 2013. № 1(37). С. 93-98.
- Тихонов В.С., Абрамов А.А. Поперечные колебания гибкой нити переменной длины в потоке//Вестник МГУ. Сер. 1, 1993. № 5. С.45-48.
- Анисимов В.Н., Литвинов В.Л. Математические модели продольно-поперечных колебаний объектов с движущимися границами//Вестн. Сам.гос. техн. ун-та. Сер. Физ-мат. науки. 2015. Т. 19. № 2. С. 382-397.
- Кечеджиян Л.О., Пинчук Н.А., Столяр A.М. Об одной задаче математической физики с подвижной границей//Извест. вузов. Северо-Кавк. регион. Естеств. науки. 2008. № 1. C. 22-27.


