Продольные резонансные колебания вязкоупругого стержня переменной длины
Автор: Анисимов В.Н.
Статья в выпуске: 4, 2017 года.
Бесплатный доступ
Исследуются колебания стержня, сгорающего с одного конца. Объект исследования относится к широкому кругу колеблющихся одномерных объектов с движущимися границами и нагрузками. Для описания колебаний использована классическая математическая модель, учитывающая вязкоупругость на основе структурной модели Фойгта. Введение безразмерных переменных позволило сократить число параметров, от которых зависит процесс колебаний, до двух. Параметры характеризуют скорость движения границы и вязкоупругие свойства стержня. Для решения применён метод Канторовича-Галёркина. В качестве динамических мод взяты собственные функции краевой задачи с неподвижной границей. Решение в случае, когда скорость движения границы равна нулю, является точным. При увеличении скорости движения границы погрешность решения увеличивается. Пренебрежение малыми величинами позволило получить сравнительно простое выражение для амплитуды резонансных колебаний. Выражение, полученное для амплитуды колебаний, содержит интегралы, не имеющие аналитического решения, поэтому они находились численно. Решение имеет модовую структуру, что позволяет анализировать резонансные свойства стержня. С помощью полученного решения проанализированы явления установившегося резонанса и прохождения через резонанс. Для установившегося резонанса получено аналитическое выражение, описывающее увеличение амплитуды колебаний. Прохождение через резонанс проанализировано количественно. Представлены графики изменения амплитуды колебаний в резонансной области для первой динамической моды при различных значениях параметра, характеризующего вязкоупругость. Представлены также графики максимальной амплитуды колебаний при прохождении через резонанс на первой динамической моде в зависимости от параметров, характеризующих вязкоупругость и скорость движения границы
Колебания объектов с движущимися границами, краевые задачи, математические модели, резонансные свойства
Короткий адрес: https://sciup.org/146211706
IDR: 146211706 | УДК: 534.11 | DOI: 10.15593/perm.mech/2017.4.01
Текст научной статьи Продольные резонансные колебания вязкоупругого стержня переменной длины
PNRPU MECHANICS BULLETIN
В статье исследуются резонансные свойства стержня, сгорающего с одного конца. Объект исследования относится к широкому кругу колеблющихся одномерных объектов с движущимися границами [1–20, 24–26, 30–32, 34, 35] и нагрузками [27–29, 33]. Такие объекты широко распространены в технике. Это канаты грузоподъёмных установок [2, 10], гибкие звенья передач [1], балки [3, 16], лентопротяжные механизмы [12], конвейеры [14, 16] и т.д. Наличие условий на движущихся границах делает неприемлемыми для решения известные методы математической физики, пригодные для задач с фиксированными границами. Точные решения получены только для волнового уравнения при ограниченном числе законов движения границ [4, 6]. Для решения в основном используются приближённые методы [2, 20]. Сложность получаемых решений объясняет тот факт, что только в ограниченном числе работ приводятся количественные результаты. В основной массе работ вязкоупругие свойства колеблющегося объекта не учитываются. Для описания колебаний использована классическая математическая модель [2, 19]. При решении использовался метод Канторовича–Галёркина [3, 5, 7, 21]. В отличие от асимптотических методов [2, 20] решение имеет модовую структуру, что позволяет анализировать резонансные свойства стержня. Пренебрежение малыми величинами позволило получить сравнительно простое выражение для амплитуды резонансных колебаний. С помощью полученного выражения проанализированы явления установившегося резонанса и прохождения через резонанс. Результаты анализа представлены в виде графиков. Решение произведено в безразмерных переменных, что позволяет использовать полученные количественные результаты для анализа колебаний технических объектов.
1. Постановка задачи
Схема объекта изучения изображена на рис. 1. Для модели введены следующие обозначения: ρ – объёмная плотность материала стержня; S – площадь поперечного сечения; E – модуль упругости; μ – коэффициент, характеризующий свойство вязкоупругости материала стержня на основе структурной модели Фойгта; l ( t ) – длина стержня, находящегося в недеформированном состоянии, в момент времени t .
Обозначим Z ( x , t ) – смещение точки стержня с координатой x в момент времени t . Математическая модель, описывающая продольные колебания стержня, имеет вид [2]
p Zu ( x , t ) - EZ xx ( x , t ) - vZ xxt ( x , t ) = 0;
Z (0, t ) = 0;
ESZ x ( l ( t ), t ) = P0 ( 1 + A cos W0(t ) ) .
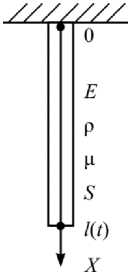
Рис. 1.Схема объекта изучения
Fig. 1. Scheme of the studied object
В настоящее время актуальной является
про-
блема изучения динамических свойств стержней из вязкоупругих материалов [22, 23]. Рассматриваемая модель может быть использована для описания колебаний стержня твердого топлива, сгорающего
с
одного конца. В этом случае P 0 –
средняя реактивная сила, а составляющая AP 0 cos W 0 ( t ) характеризует слабые возмущения гармонического характера, связанные с пульсационной составляющей тяги внутрикамер-ного процесса. Малый коэффициент А показывает, во сколько раз амплитуда возмущений больше P 0 ; W 0 ( t ) – монотонно возрастающая функция.
Закон движения границы примем равномерным: l(t) = -v0t +1(0). Здесь l(0) - перво- начальная длина стержня; v0 – скорость движения границы.
Введём безразмерные переменные
^ = —; т = — t ; Z(x , t ) = P-1 (0) U (^, t) + ^); a = 4 E .
l (0) l (0) ( ) ES ( ( ) ) Vp
В результате задача (1)–(3) примет следующий вид:
U тт ( ^, т ) — U S ( ^, т ) — £ 1 U St ( ^,т ) = 0;
U (0, t ) = 0;
U^ (L ( b0 т), т) = A cos W(t), где
£i = —-— ; £0 = —; —1- l ( t ) = L ( £от ) = 1 - £от; W (t) = W o | 1 (00 т | .
-
1 a p l (0) 0 a l (0) ( 0 ) 0 0 ( a )
Здесь £ 0 , £ 1 - малые параметры. Параметр £ 1 характеризует малость сил внутреннего трения по сравнению с упругими силами. Параметр £ 0 характеризует малую скорость движения границы по сравнению со скоростью звука в стержне.
Деформации стерня определяются следующим выражением:
Zx (x, t) = -PS (U5 (5, т) +1).(4)
Чтобы преобразовать граничные условия к однородному виду, введём новую функцию
U (5, т ) = V (5, т) + Aicos W (т), где V (5, т) удовлетворяет уравнению
-
[V (5 Т) + Aicos W(т)]тт - V=5 (5 Т) - £V(5 Т) = 0
и граничным условиям
-
V(0, t) = 0 ; V (L (£0т), т) = 0.(6)
-
2. Решение задачи
Решение будем производить с точностью до членов второго порядка малости порядка малости. Для решения задачи (5), (6) будем использовать метод Канторовича-Галеркина [5]. Решение будем искать в виде
ю
V ( 5, т ) = Е f . (т) Х п ( 5, £ 0 т ) , (7)
n = 1
где
Xn ( 5, £ 0 т ) = sin ( “ n ( £ 0 т ) 5 ) , (8)
Ю n ( £ 0 т )
п n - п/2
L ( £ 0 т ) .
Заметим, что функции (8) при £ 0 = 0 и £ 1 = 0 являются собственными формами колебаний. В этом случае метод Канторовича-Галёркина дает точное решение. При увеличении £ 0 точность уменьшается. Статья посвящена анализу резонансных явлений, наблюдаемых на одной из собственных частот. Амплитуда колебаний на резонансной частоте многократно увеличивается. Амплитуда колебаний на нерезонансных частотах соизмерима с возмущающими воздействиями. При этом нерезонансными членами ряда (7) можно пренебречь и рассматривать решение только на одной резонансной моде.
После подстановки члена с порядковым номером п ряда (7) в уравнение (5) получим
[. f n (т) X n ( 5 £ 0 т ) + A 5cos W (т) ] тт + ® n ( £ 0 т ) f n (т) X n ( 5, £ 0 т ) +
+ £Х (£ 0 т) f n '( т ) X n ( 5, £ 0 т ) = 0
При наблюдении резонансных явлений W (т) = Qt + 0 ( £ 0 т ) , где 0 ( £ 0 т ) - функция медленного времени [2], а Q - усреднённая частота внешнего воздействия. Пренебрегая членом порядка £ 0 , получим
( cos W (т) ) " = - ( W '(т) ) 2 cos W (т). (9)
Согласно методу Канторовича-Галёркина, умножим полученное уравнение на X n ( ^, £ 0 т ) и проинтегрируем по d ^ в интервале от нуля до L ( £ 0 т ) . Учитывая (9), с точностью до членов второго порядка малости получим следующее уравнение для определения функций f n (т):
/ - "( т) + 2 R - ( £ 0 т ) f n ' (t) + ® ( £ 0 т ) f n (t) = P n ( £ 0 т ) cos W (т),
где
_ f _ n 1
£ , I I
R = _ £ 0 L ( £ 0 T) + V 2 7 , - ( ) 2 L ( £0 т ) 2 L 2 ( £0 т ) ,
Pn ( £0 т ) =
2 A ( - 1) - + 1 L ( £ 0 т )
x 2
n 1 n - —
2 J
( W ' (т) ) 2.
Если ввести в уравнение (10) новую функцию f-(т) = C-(т)У-(т),
где
f T 1
C - (т) = exp - j R - ( ; ) d q = ^ L ( £ 0 T ) exp
_ f П 1
£ П -T
-
1 V 2 J
-
2 L ( £ 0 T )
,
V
то оно не будет содержать члена с первой производной:
У "(т) + ® 2 ( £ 0 т ) У - (т) = D - (T)cos W (т).
Здесь
D- (t) =
2 A ( - 1) - + 1 ^L ( £ 0 т )
X 2
П 1 n - —
2 J
( W ' ( t) ) 2 exp
_ f П 1
£ П -T
1 V 2 J
2L (£0T)
•
Два линейно независимых решения однородного уравнения, соответствующего уравнению (12), c точностью до членов второго порядка малости имеют вид у-1(т) = a- (£0т)cos (w-(т)); у-2(т) = a- где
w-(t) = J®- (£0T)dT =--
) ; a - ( £ 0 т ) =
£0
Решение уравнения (12) при нулевых начальных условиях имеет вид
, . . / , Vtf Dn ( ^ ) cos ( wn ( ^ ^ cos ( W ( ^ )),/ fn (Т) = - Cn (Т) an ( 60 Т ) sin ( wn (Т) ) I -----------Т ------ d^ -
О ® n ( 6 О ? ) a n ( 6 О Т )
А / /чЧГ D n ( ^ ) sin ( w n ( ^ )) cos ( W ( ^ ^Л
-
- C n (Т) a n ( 6 О Т ) cos ( w n (т) ) I ----------- 7 ------ d ^ .
О ® n ( 6 О ? ) a n ( 6 О Т )
Пренебрегая нерезонансными членами, как это сделано в работе [5], получим следующее выражение для амплитуды вынужденных колебаний:
4 2 (1) = A 2 Е ^(т) J F n ( Z ) cos ( Ф п ( Z ) ) d Z + J F n ( Z ) sin ( Ф п ( Z ) ) d Z) 2 .
к 0
Функции, входящие в выражение (13), определяются следующими выражениями:
I n 1
6. n n — T
1 к 2 7
L ( 6 0 T )
;
L 2 ετ
E 2(T) = ^^4? exp
I n 1 nn — к 2 7
F n ( Z ) = A ( - 1) n + 1 L ( e „ т ) exp
_ I n 1
£, П n T
-
1 к 2 7
-
2 L ( £ 0 T )
( W ‘ (т) ) 2 ;
π n n
Ф n ( Z ) = 2ln ( L ( 6 0 T ) ) - W (t) .
ε 0
Амплитуда колебаний для деформаций V , ( ^, т ) имеет вид
B n (т) = 4 ® n ( 6 о т ) A n (т).
A
Величина Bn (τ) показывает, во сколько раз амплитуда колебаний деформаций превосходит интенсивность внешнего возмущения А .
3. Анализ решения
С помощью выражения (14) были проанализированы резонансные свойства объекта. В системах с движущимися границами наблюдаются два вида резонансных явлений: установившийся резонанс и прохождение через резонанс. Установившийся резонанс это явление резкого увеличения амплитуды колебаний, когда изменение частоты внешней силы и одной из собственных частот согласованы таким образом, что создаются наилучшие условия для увеличения амплитуды. Установившийся резонанс наблюдается, если Ф n ( Z ) = 0, т.е.
π п n —
W (т) =--2ln ( L ( 6 0 т ) ) .
ε 0
Изменение амплитуды колебаний при этом будет описываться следующим выражением:
τ A n, (т) = E „ (t) J F „ ( S ) d S.
Явление прохождения через резонанс наблюдается при внешнем возмущении постоянной частоты W (т) = Qt. Это явление резкого увеличения амплитуды в течение конечного промежутка времени, когда мгновенная частота одного из собственных колебаний проходит через значение возмущающей частоты. На рис. 2 представлен процесс увеличения амплитуды колебаний в резонансной области на первой динамической моде при £ 0 = 0,0001. Возмущающая частота Q подбиралась таким образом, чтобы прохождение через резонанс начиналось при т = 0.
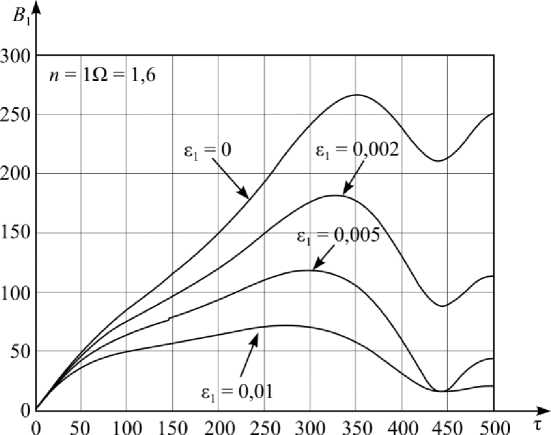
Рис. 2. Процесс увеличения амплитуды колебаний при прохождении через резонанс на первой динамической моде
Fig. 2. Increase of the amplitude of fluctuations when passing through the resonance at the first dynamic mode
Выражение (14) было численно проанализировано на максимум. На рис. 3 изображена зависимость максимальной амплитуды колебаний при прохождении через резонанс на первой динамической моде от ε 0 и ε 1 .
Оценим погрешность метода Канторовича–Галёркина. Рассматриваемая задача без учета вязкоупругости (8 1 = 0) в работе [6] была решена точным методом. Там было получено следующее выражение для функции W (τ), при которой возникает установившийся резонанс:
π п n —
W (т) =-- / 2 J n ( L ( 8 0 т ) ) .
In 8
v 1 - 8 0 )
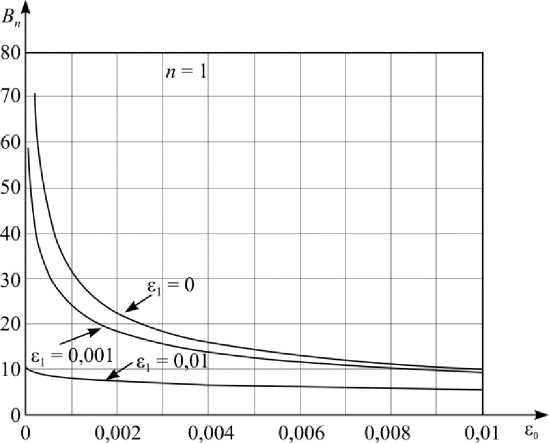
Рис. 3. Зависимость максимальной амплитуды колебаний при прохождении через резонанс на первой динамической моде Fig. 3. Dependence of the maximum amplitude of fluctuations when passing through the resonance at the first dynamic mode
Сравнением данного выражения с выражением (15) при различных значениях ε 0 установлено, что относительная погрешность W (τ) в равномерном приближении не превосходит 5 % при ε 0 < 0,37.
Заключение
Таким образом, в отличие от асимптотических методов, использование метода Кан-торовича–Галёркина позволило получить решение, имеющее модовую структуру. Это актуально при анализе резонансных свойств объекта. Пренебрежение малыми членами дало возможность получить сравнительно простое выражение для амплитуды колебаний.
Список литературы Продольные резонансные колебания вязкоупругого стержня переменной длины
- Cамарин Ю.П., Анисимов В.Н. Вынужденные поперечные колебания гибкого звена при разгоне//Изв. вузов. Машиностроение. -1986. -№ 12. -С. 17-21.
- Горошко О.А., Савин Г.Н. Введение в механику деформируемых одномерных тел переменной длины. -Киев: Наукова думка, 1971. -270 с.
- Лежнева А.А. Изгибные колебания балки переменной длины//Изв. АН СССР. Механика твердого тела. -1970. -№ 1. -С. 159-161.
- Весницкий А.И. Волны в системах с движущимися границами. -М.: Физматлит, 2001. -320 с.
- Анисимов В.Н., Литвинов В.Л. Исследование резонансных свойств механических объектов при помощи метода Канторовича-Галёркина//Вестн. Самар. гос. техн. ун-та. Сер. Физ.-мат. науки. -2009. -№ 1 (18). -С. 149-158.
- Анисимов В.Н., Литвинов В.Л., Корпен И.В. Об одном методе получения точного решения волнового уравнения, описывающего колебания систем с движущимися границами//Вестн. Самар. гос. техн. ун-та. Сер. Физ.-мат. науки. -2012. -№ 3 (28). -С. 145-151.
- Ding Hu, Chen Li-Qun. Galerkin methods for natural frequencies of high-speed axially moving beams//J. Sound and Vibr. -2010. -No. 17. -P. 3484-3494.
- Kotera Tadashi Vibration of a string with time-varying length//Bulleten Japan Sosietyof Mechanical Engineers. -1978. -Vol. 21. -No. 162. -P. 1677-1684.
- Zhu W.D., Zheng N.A. Exact response of a translatingstring with arbitrarily varying length under general excitation//Trans. ASME. J. Appl. Mech. -2008. -Vol. 75. -No. 3. -P. 519-525.
- Zhu W.D., Chen Y. Theoretical and experimental investigation of elevator cable dynamicsand control//Trans. ASME. J. Vibr. And Acoust. -2006. -No. 1. -P. 66-78.
- Nonlinear vibration analysis of an axially moving drill string system with time dependent axial load and axial velocity in inclined well/S.M. Sahebkar, M.R. Ghazavi, S.E. Khadem, M.H. Ghayesh//Mech. and Mach. Theory. -2011. -No. 5. -P. 743-760.
- Boyle John. M. (Jr), Bhushan Bharat. Vibration modeling of magnetic tape with vibro-impact of tape-guide contact//J. Sound and Vibr. -2006. -No. 3. -P. 632-655.
- Zhang P., Zhu C.M., Zhang L.J. Analyses of longitudinal vibration and energetic on flexible hoisting systems with arbitrarily varying length//Journal of Shanghai Jiao-Tong University. -2008. -No. 42 (3). -P. 481-488.
- Nguyen Q.C., Hong K.S. Transverse vibration control of axially moving membranes by regulation of axial velocity//IEEE Transactions on Control Systems Technology. -2012. -No. 20 (4). -P. 1124-1131.
- Zhang Y.H. Longitudinal vibration modeling and control a flexible transporter system with arbitrarily varying cable lengths//Journal of Vibration and Control. -2005. -No. 11. -P. 431-456.
- Chen S.H., Huang J.L. On internal resonance of nonlinearvibration of axially moving beams//Acta Mechanica Sinica. -2005. -Vol. 37. -No. 1. -P. 57-63.
- Nguyen Q.C., Hong K.S. Transverse vibration control of axially moving membranes by regulation of axial velocity//IEEE Transactions on Control Systems Technology. -2012. -No. 20 (4). -P. 1124-1131.
- Тихонов В.С., Абрамов А.А. Поперечные колебания гибкой нити переменной длины в потоке//Вестн. МГУ. Сер. 1. -1993. -№ 5. -С. 45-48.
- Анисимов В.Н., Литвинов В.Л.Математические модели продольно-поперечных колебаний объектов с движущимися границами//Вестн. Самар. гос. техн. ун-та. Сер. Физ-мат. науки. -2015. -Т. 19, № 2. -С. 382-397.
- Кечеджиян Л.О., Пинчук Н.А., Столяр A.М. Об одной задаче математической физики с подвижной границей//Изв. вузов. Северо-Кавказ. регион. Естеств. науки. -2008. -№ 1. -C. 22-27.
- Мышкис А.Д. Математика для технических вузов. -СПб.: Лань, 2002. -640 с. Янкин А.С. Влияние частот бигармонического (двухчастотного) нагружения на динамическое поведение полимерных композитов//Вестник Пермского национального исследовательского политехнического университета. Механика. -2015. -№ 4. -С. 273-292.
- Янкин С.В., Словиков С.В., Бульбович Р.В. Определение динамических механических свойств низкомодульных вязкоупругих композитов при бигармоническом законе нагружения//Механика композитных материалов и конструкций. -2013. -Т. 19, № 1. -С. 141-151.
- Lei X.-Y. Effects of abrupt changes in track foundation stiffness on track vibration under moving loads//Zhendong Gongcheng Xuebao=Journal of Vibration Engineering. -2006. -Vol. 19. -No. 2. -P. 195-199.
- Brake M.R., Wickert J.A. Frictional vibration transmission from a laterally moving surface to a traveling beam//J. Sound and Vibr. -2008. -Vol. 310. -No. 3. -P. 663-675.
- Рагульский К.И. Вопросы динамики прецизионных лентопротяжных механизмов//Динамика машин. -М.: Наука, 1971. -С. 169-177.
- Ерофеев В.И., Лисенкова Е.Е. Возбуждение волн нагрузкой, движущейся по поврежденной гибкой одномерной направляющей, лежащей на упругом основании//Проблемы машиностроения и надежности машин. -2016. -№ 6. -С. 14-18.
- Ерофеев В.И., Колесов Д.А., Лисенкова Е.Е. Генерация волн источником, движущимся по деформируемой направляющей, лежащей на упруго-инерционном основании//Машиностроение и инженерное образование. -2014. -№ 2 (39). -С. 37-40.
- Ерофеев В.И., Колесов Д.А., Лисенкова Е.Е. Исследование волновых процессов в одномерной системе, лежащей на упруго-инерционном основании, с движущейся нагрузкой//Вестн. науч.-техн. развития. -2013. -№ 6 (70). -C. 18-29.
- Анисимов В.Н. Продольные резонансные колебания вязкоупругого каната грузоподъёмной установки//Изв. Самар. науч. центра Российской академии наук. -2016. -Т. 18, № 4-1. -С. 128-133.
- Самарин Ю.П. Об одной нелинейной задаче для волнового уравнения в одномерном пространстве//Прикладная математика и механика. -1964. -Т. 26. -Вып. 3. -С. 77-80.
- Bergamaski S., Sinopoli A. On the flexural vibration of arms with variable length. On exact solution//Mech. Res. Commun. -1983. -Vol. 10. -No. 6. -Р. 342-344.
- Фирсанов В.В. Динамическое состояние системы балок с переменными параметрами при действии подвижной нагрузки//Вестн. Моск. авиац. ин-та. -2009. -№ 3. -Р. 138-144.
- Николаи Е.Л. О поперечных колебаниях участка струны, длина которого равномерно изменяется: тр. по механике. -М.: Гостехиздат, 1955. -C. 328-331.
- Литвинов В.Л. Поперечные колебания вязкоупругого каната, лежащего на упругом основании, с учетом влияния сил сопротивления среды//Вестн. науч.-техн. развития. 2015. -№ 4 (92).


