Продольные вибрации в двухслойном стержне при наличии между слоями сухого трения

Стержень состоит из двух однородных слоев, прижатых друг к другу равномерно распределенным постоянным давлением.

• 1.    Исследуем распространение продольных вибраций в каждом из слоев составного стержня конечной длины при воздействии гармонических возмущений частоты ω . Для контактных поверхностей полагаем справедливым закон Кулона, а для материала стержня – закон Гука [4]. Поставленная задача решается с использованием приближенных методов гармонической линеаризации и разложений по малому параметру. Уравнения динамики слоев имеют вид:

ρ Q_ju && _j - EQ_ju ′ _j ′= ( - 1)^jqsign(u & ₁ - u & ₂). j = 1,2 (1.1)

Здесь ρ – плотность материала, Q ₁ и Q ₂ – площади сечений слоев, u ₁( x , t ) и u ₂( x , t ) – смещения слоев стержня, q – сила трения, отнесенная к единице длины контакта стержня, E – модуль упругости. Штрихом и точкой обозначены частные производные по координате x и времени t. Полагаем, что относительные вибрации η ( x , t ) = u ( x , t ) - u ( x , t ) распространяются на 1              2

всю длину составного стержня. Условия, обес- печивающие это допущение, определим ниже. Рассматривая стационарные колебания, решение для относительных смещений будем искать в виде

η(x, t) = a(x)сos(ωt +ϕ(x)).(1.2)

Предварительно, следуя методу гармонической линеаризации, нелинейную функцию в системе (1.1) заменим линейной

Здесь коэффициент линеаризации r вычислен по формуле [3] и имеет вид

• 1    2π4

r =    ∫ F(-aωsinϕ)sinϕdϕ=  .

πa 0                 πa

&& - c ² n " = - ( q i + q ₂) Пto      c ² = El P ,  (1.6)

Решение системы (1.5–1.6) будем искать в комплексной форме, что стало возможно после линеаризации задачи: физический смысл имеет вещественная часть решения. Для общности и удобства вычислений предварительно перейдем к безразмерным величинам. Введем обозначения

| Z = R, a = to) c, у = ax, Kj=qj!to\ K=q+q2)/to2.

(1.7)

Решения системы (1.5–1.6) будем искать в виде

П = KZ exp(itot), u2 = K2D exp(itot),

U 1 = q + u 2, | KZ | = a.             ^(L8)

После подстановки искомых решений в систему и принятых обозначений получим для комплексных амплитуд Z и D :

Z " + Z = iZj\z\ , D " + D = - iZ/Z     (1.9)

(Штрихом в уравнениях обозначены производные по координате y .)

Решение первого уравнения системы (1.9) для комплексной амплитуды Z относительных смещений будем строить методом вариации произвольных постоянных. За порождающее решение примем решение уравнения без правой части

Z = A_Yexp(i ^ i ) + A 2 exp( - / £), 4 j = у + ф , , (1.10)

где A 1 , A₂, y 1 , y ₂ - постоянные интегрирования. Полагая постоянные функциями координаты y и накладывая дополнительные условия на производные (1.11):

A ехР(5)+A2 e*4 +    (111)+Ai ф expi 4) - A2i ф2 exp(-i 42)=0.   .

Подставим искомое решение (1.10) в первое уравнение (1.9) и с учетом (1.11) получим систему уравнений для отыскания функций:

A = ( - 1) j + 1 1 S R , ф‘ = ( - 1) j S R

3         2 dAj   j         2Aj2 64j

R = ( A 12 + A 22 + 2 A 1 A ₂cos 4 )¹²,       ^(1.12)

4= 41+42, R=Z.

Найти непосредственно решение системы (1.12) в замкнутом виде не удается. Для разрешения системы во спользуемся методом усреднения. В работах Миронова и Пальмова показано, что при слабом демпфировании в рассматриваемом случае можно считать колебания медленно меняющимися как по координате, так и по времени [2], [3]. Поэтому целесообразно в системе провести усреднение по быстрой переменной 4, при этом предполагается медленное изменение переменных A 1, A2, ф1 и ф2. Для проведения усреднения в системе (1.12) возьмем среднеквадратическое значение функции R.

R R!=(—2^ R2d4)12=^AF+A22.   (1.13)

2п о

После подстановки R в (1.12) усредненная система примет вид

A j = ( - 1) j + 1 A j /2 { R ) , ф 1 = 0, , ф 2 = 0.     (1.14)

Данная система имеет интегралы ф1 = c3, ф2 = С4, A1A2 = c2, (AO2+(A2)2 = 14.

(1.15)

Однако получить в явном виде зависимость A1 и A2 от y в элементарных функциях не удается. Как следует из интегралов (1.15), зависимость между A1 и A2 определяется равнобочной гиперболой и при приложении возмущения реализуется одна из ветвей гиперболы. При этом отношение

£ = A l/ A 2 = c 2/ A 2 ⁽¹-¹⁶⁾ будет изменяться от единицы при x = l , где A 1 = A ₂ , 4 + 4 2 = 0 , и резко уменьшаться при изменении величин A 1 и A 2 , то есть 1 >  £> 0. B этом можно убедиться после вычисления постоянных интегрирования, которые будут определены далее. Если уравнения системы (1.14) разложить по параметру £ , учитывая величины не выше £ , придем к системе

A = A 1/ 2 A 2 , A 2 = - 12, ф; = 0, ф 2 = 0.    (1.17)

Введенный параметр £ делает систему (1.17) близкой к системе (1.14). Действительно, при £ =1 система (1.17) перейдет в систему (1.14), а при малых значениях £ - вследствие ее малой величины. Система (1.17) имеет решение

A 2 = c 1 - У /2, 4 = c2К c 1 - У/ 2), Ф 1 = c 3 , Ф 2 = c 4 .

(1.18)

При этом для амплитуды относительного смещения R = Z с учетом отношения (1.16) можно записать:

R = c 1 - у /2+ c ₂/( c 1 - у /2)cos(2 y + c ₃ + c ₄). (1.19)

Для определения выражений для смещения слоев стержня u 1 и u 2 обратимся к системе (1.9). Если ввести переменные V=Z+D и D=V–Z, то получим дифференциальное уравнение для V:

V' ' + V = 0 .                (1.20)

Уравнение имеет решение

V = c ₇exp( 4 3 ) + c 8 exp( - 4 4 ),         (1.21)

§3 = У + c5, §4 = У + c6.

Тогда для функций u1 и u2 можно записать решение в комплексной форме u1 — (KZ + K2 D) exp(z rot), u 2 — K2 (V - Z) exp(z rot).

(1.22)

Входящие в эти перемещения функции определены выше. Они содержат постоянные интегрирования cj, которые должны быть определены из граничных условий. Граничные условия для такого составного стержня могут быть весьма разнообразны. Рассмотрим составной стержень длины l. При этом предполагаем, что относительные вибрации между слоями будут распространяться на всю длину стержня. Зададим кинематические граничные условия в комплексной форме u1(0, t) = H1 exp( zrot), u 2(0, t) = H2exp( zrot),     (x=0)    (1.23)

u 1 (l , t) — 0, u ₂( l , t) — 0 .      ( x=l)

Из этих граничных условий определяются постоянные интегрирования.

C 3 + c 4 — —2 L, C 5 + С б — —2 L, c₂ — — ( c 1 — L /2)², c₇ — — c₈, c₇ — X) 2sin L,

X — (H2Q2+HQ\roxpQ 4Q +Q2)q, tgC3 — Ci2sin2 L / s,             (1.24)

s — ( c 1 — L /2)² — c 1 ² cos 2 L , tgc₅ — ctgL,

L — a l , H — ( H 1 — H 2 )/ K , c ² + ( c 1 — L / 2)⁴ / c ² — 2( c 1 — L / 2)² cos 2 L — H .

Постоянная интегрирования с 1 определяется из последнего выражения системы (1.24) численным методом или из приближенного выражения при учете отношения (1.16):

c 1 — ( c i — L / 2 ) 2 cos(2 L ) / q — H .        (1.25)

Выражение (1.25) получено из (1.19), определяющего равенство амплитуды относительного смещения и амплитуды относительного возмущения на конце стержня, при x=0. При этом берется значение c1 > 0. Сравним полученное решение для амплитуды относительного смещения R(y) с результатом численного интегрирования первого уравнения системы (1.9). На фиг. 1 представлены зависимости R(y) в безразмерной форме. Сравнение выполнено при одинаковых граничных условиях и постоянном по длине давлении для нескольких значений амплитуд возмущающих воздействий на конце стержня при условии, что вибрации распространяются по всей длине рассматриваемого стержня. Сплошными линиями показаны результаты численного интегрирования, штриховыми – приближенного решения. Из представленной графической зависимости видно, что расхождение невелико.

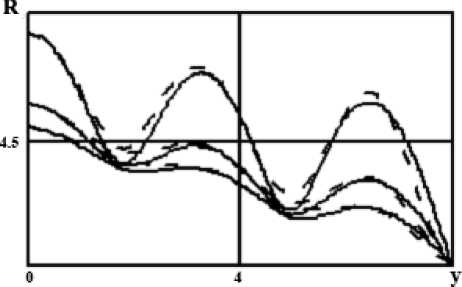
Фиг. 1

2. Определим параметры системы и внешнего воздействия, обеспечивающие распространение относительных вибраций на всю длину l рассматриваемого стержня. Для этого рассмотрим полубесконечный стержень с кинематическим граничным условием

7 (0, t ) — ( H 1 — H ₂)exp( z ro t ) . ( x=0)    (2.1)

Решение для относительных смещений будем искать также в виде (1.2). В рассматриваемом случае удается найти решение [4], содержащее две постоянные интегрирования с 1 , с 2 и удовлетворяющее убыванию амплитуды с ростом x . Для комплексной амплитуды относительных смещений решение уравнения (1.9), тождественно удовлетворяющее ему, имеет вид:

Z — ( c 1 — y /2 ) exp( — z ( y + c ₂)).         (2.2)

Тогда для относительных смещений в действительной форме запишем

П ( x, t ) — K ( c 1 — y / 2) cos( ro t — y — c 2 ).     (2.3)

Удовлетворяя граничному условию (2.1), постоянные интегрирования примут значения c — ( H — H )/ K , c. — 0 , а зона распростране- 1   12    2

ния относительных вибраций определится из условия положительности амплитуды

x * — 12( H 1 — H 22 )c ronp Q 1 Q 2 q - 1 ( 8 1 + Q 2 ) ^{— 1}. (2.4)

Следовательно, решение (2.3) справедливо для значений 0 <  x <  x * . При x >  x * следует принять n ( x , t ) — 0 , то есть сечения Q 1 и Q 2 будут совершать вибрации совместно без относительных смещений слоев. Заметим, что если q ^ 0 , координата x * ^^ , что соответствует отсутствию демпфирования. При больших значениях q вибрации локализируются около возмущенного конца стержня. Как следует из (2.4), величина x _* зависит от частоты воздействия ro . Поэтому для распространения вибраций на длину стержня l необходимо значение частоты, равной не менее ro — ro _* .

ω * = 2 q ( Q 1 + Q 2 ) l /( H 1 - H 2 ) c πρ Q 1 Q 2 .     (2.5)

Следовательно, если проследить за вибрациями в составном стержне длиной l при изменении частоты от нуля до частоты ω > ω _* , то сначала необходимо воспользоваться решением (2.3), а при достижении частоты до ω = ω _* – решением для системы (1.12). Далее отметим, что если в исходной системе заменить u ₂ = 0 ^, а η ( x , t ) = u ₁( x , t ) ^, то автоматически получим решение задачи о распространении вибраций в стержне конечной длины, прижатом к неподвижной шероховатой поверхности [1].

3. Рассмотрим необратимые потери в составном стержне при вибрациях составного стержня. Эти потери могут быть определены как работа сил трения на относительном смещении

W = 4 qK ∫ ^x R ( y ) dx =

4qK

S ( y ). α

(3.3)

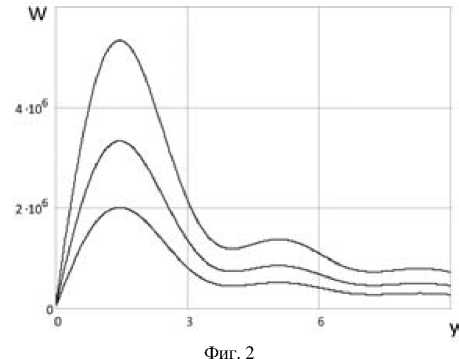
Здесь S(y) – площадь под графиком для амплитуды относительных смещений, ограниченной координатой y = α x , при фиксированном значении x, равном значению длины L рассматриваемого стержня. На фиг. 2 представлено несколько зависимостей потерь на трение от координаты y = ω L/c для различных значений величины силы трения q. Зависимости показывают, что потери существенно зависят от величины трения и частоты внешнего воздействия ω .

слоев по длине стержня за период возмущающего воздействия:

x 2 π ω

W = ∫∫ F Тр 00

∂η

dtdx .

∂t

(3.1)

Силу трения возьмем c учетом ее линеаризации в виде

F Тр = - qsign η & =

. π KR ω

(3.2)

Вычисление потерь по формуле (3.1) дает

выражение