Продвижение воды в системе несимметричных линейных капилляров

Введение. В настоящее время изучены физиологические процессы, обеспечивающие рост и развитие растений. Однако практически не представлены систематические исследования движения воды в капиллярных сетях растений во взаимосвязи с их внешним видом. Достаточно хорошо изучено движение воды в системе «почва — растение — атмосфера» [1]. Находящаяся в почве свободная вода под действием сил осмоса через корневые волоски поступает в паренхиму корня. Далее основная часть (90 %) этой воды по капиллярам (сосудам стебля и веток) восходящим током поднимается к листьям. Основная часть восходящей воды идёт по сосудам ксилемы. Однако ксилема высших растений не является набором простых вертикальных трубок, а представляет собой более сложную структуру [2]. Об этом свидетельствуют многочисленность и многообразие жизненных форм растений.

В [3] была рассмотрена математическая модель распределения жидкости в симметричных ветвящихся капиллярных системах, позволившая выявить основные закономерности данного процесса:

• —    наибольшее продвижение воды имеет место в ветвях нижнего уровня;

• —    наличие боковых ветвей позволяет увеличить высоту подъёма воды в вертикальном капилляре по сравнению с одиночным капилляром равного радиуса;

• —    фигура, образуемая при последовательном соединении водных менисков в капиллярных ветвях, своею конической формой напоминает лист или дерево.

Цель работы. Показать, что модели идеализированных симметричных ветвящихся капиллярных систем имеют границы применимости. Ограничения, возникающие при идеализации этих систем, устраняются в несимметричных ветвящихся капиллярных системах. При этом остаются справедливыми основные закономерности распределения воды в ветвях, описанные в [3].

Теоретическая модель. Рассмотрим N -уровневую симметричную капиллярную систему (рис. 1). Предположим равными радиусы r вертикального капилляра и боковых ветвей, углы наклона боковых ветвей β i , расстояния h 1 между ветвями соседних уровней. Погрузим вертикальный капилляр в воду так, чтобы расстояние от поверхности воды до начала ветвей первого уровня также было равно h 1 . Определим, капилляры каких n уровней будут заполнены водой при разных величинах h 1 . Воспользуемся выражением (29), полученным в [3] для определения высоты подъёма воды H nN ) в вертикальном капилляре симметричной системы в виде

H N ) = h + knh - kh ^ "„ ) 2,1 + 1, (1) полагая при этом, как и в [3], h 1 = kh , а 0 ≤ k ≤ 1.

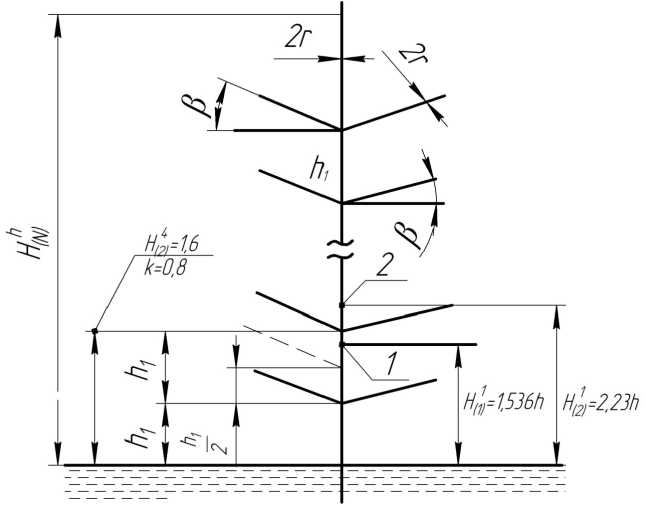
Рис. 1. N -уровневая симметричная капиллярная система

Расстояние от поверхности воды до уровня n +1 можно определить из соотношения

H N = ( n + 1 ) kh.                                     (2)

Вычитая из (2) выражение (1), получим

H N - H ( n ) = ^h [ ^k ^ 1 + L П^2П1Г1 )- ¹ ) .                       ⁽³⁾

Процесс подъёма воды в незаполненный капилляр, описываемый выражением (3), состоит в следующем. Вода изначально поднимается в нижней части вертикального капилляра до ветвей первого уровня под действием единственной силы поверхностного натяжения воды в мениске. Достигнув ветвей первого уровня, движение воды в системе происходит уже под действием трёх сил поверхностного натяжения, и силы перераспределяются, что обеспечивает увеличение высоты подъёма воды в вертикальном капилляре [3]. Когда жидкость достигает наклонных боковых капилляров второго уровня, происходит их заполнение и дальнейшее перераспределение действующих в системе сил, как следует из выражения (1). Условием окончания подъёма воды в вертикальном капилляре служит неравенство

H N1 - ^H nN ) = h [ k [ 1 + 2 "N ) n+1 )- 1 )> 0.                       (4)

Несложными преобразованиями (4) приводится к виду

² " N ) 2^1 >  k - ^{L                              (5)}

В табл. 1 приведены величины k , соответствующие им значения правой и левой частей неравенства (5), а также количество возможных уровней n в системе. Величина членов ряда под знаком суммы и разность между каждым предыдущим и последующим членом монотонно убывают по мере увеличения n . Сумма первых двенадцати членов этого ряда равна 1,268.

Таблица 1

Расчётные значения количества возможных уровней

k	0,2	0,3	0,4	0,5	0,6	0,7	0,8
1/ k – 1	4	2,33	2,25	1,00	1,66	0,14	0,12
n 2 — ( N ) 2 n + 1	<1,5	<1,5	<1,5	1,02	0,66	0,42	0,25
n	>12	>12	>12	8	3	2	1

Из таблицы видно, что при малых значениях k вода достигает высоких уровней. Но при k = 0,8 вода в системе до второго уровня не поднимется — заполнены водой будут только ветви первого уровня. Действительно, подставляя k = 0,8 в (1), получим величину подъёма воды в вертикальном капилляре после заполнения ветвей первого уровня: H ₍ 1 _N ) = 1,536 h (точка 1 на рис. 1). Боковые капилляры второго уровня расположены на высоте H N ) = 1,6h . Вода до них не поднимется. В равновесное состояние система придёт по заполнении капилляров первого уровня.

В реальных условиях в растениях этого, конечно, не происходит. Полученный результат — следствие упрощения и идеализации в [3] модели. Но если мы добавим ещё один капилляр (пунктир на рис. 1), то есть добавим асимметричный капилляр в систему, то ситуация изменится. Пусть этот капилляр имеет те же размеры, что и остальные. Примем также, что он расположен на высоте h 1 /2. Тогда уравнение равновесия воды в вертикальном капилляре в такой системе можно записать в виде

• — n r²hpg + 1n r²h p g + 1n r²h p g + n r ² H ¹. - 2h )p g = 2n r ocosa .

6 ¹¹ 8 ¹ 6 ^{1 ( 2 ) 1}

Решая это уравнение относительно высоты подъёма воды, получим H ( 2 ) = 2,23 h (точка 2 на рис. 1). То есть при наличии асимметрии вода будет поступать и в капилляры второго уровня. Наличие таких асимметричных элементов в растениях можно рассмотреть на примере молодых растений пихты Нордмана ( Abies nordmanniana ). На вертикальных стволах между параллельными ветвями разных уровней присутствуют короткие боковые отростки, не получающие дальнейшего развития. Возможно, они и являются элементами асимметрии, обеспечивающими подъём воды к капиллярным ветвям верхних уровней.

В связи с вышеизложенным следует рассмотреть математические модели распределения воды в капиллярных системах с несимметричными капиллярными ветвями.

Пусть имеется капиллярная система (рис. 2), левая и правая ветви которой смещены по вертикали на величину Δh1. Примем радиусы в обеих наклонных ветвях капиллярной системы и в её вертикальной части равными r, а их углы наклона одинаковыми и равными β. В этом случае на вертикальную часть высотой h1 будут действовать силы поверхностного натяжения обеих капиллярных ветвей. Тогда сила, необходимая для подъёма воды на высоту h1 распределится поровну в обеих ветвях, и каждая наклонная ветвь будет поднимать половину объёма воды в этой вертикальной части.

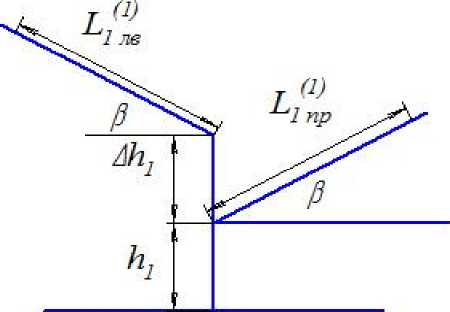
Рис. 2. Несимметричный капилляр

Введём обозначения для величин продвижения воды в правой и левой ветвях в виде Lnр и L1 Лв, а для высоты её подъёма — h^ и h^ соответственно. Уравнение равновесия воды в рассматриваемой системе можно записать для левой и правой ветвей соответственно в виде:

2 nr2h,pg + nr2/11Пppg sin в = 2nracosa(6)

2 nr2 h,p g + nr2 L1Л в Ah,p g + nr 2pg sine = 2nr acosa .(7)

Cокращая обе части уравнений на π r ²ρ g , получим:

/пр si^2^ - 2h, = h - 2hl = h* ,(8)

LL- ^=20^ " 2 h l - kh , = h - 2 h l - A h l = h^ B .                 (9)

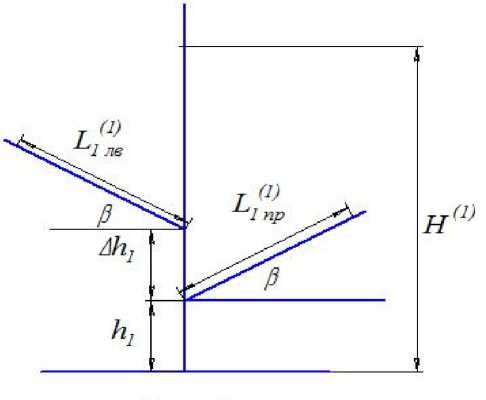
Рис. 3. Несимметричный капилляр с центральным вертикальным капилляром

Усложним капиллярную систему, добавив центральный вертикальный капилляр, как показано на рис. 3. Положим радиусы всех капилляров равными r, углы наклона капиллярных трубок равными в. Обозначим общую высоту подъёма воды в вертикальном капилляре как H(11). Объём воды в нижней части высотой h1 будет находиться под действием трёх одинаковых сил, и уравнения продвижения воды в ветвях капилляров для правой, левой и вертикальной частей могут быть записаны следующим образом:

3 nr2h1pg + nr^рppg sin в = 2nracosa,(10)

3nr2 h1p g + 2 nr 2Ah1pg + nr 'L ЛBpg sine = 2nr acosa,(11)

• 3 nr2h1pg + 2 nr2Ah1pg + nr2 (h(1 - (h1 + Ah1))pg = 2nracosa .(12)

Сокращая обе части уравнений (10)–(12) на πr2ρg и опуская промежуточные преобразования, получим:

L4, sine = h -3h = hW,(13)

L ЛB sine = h - 3 h1 - 2Ah = h«s,(14)

H^ h + 3h1 + 3Ah1.(15)

Из выражений (13)–(15) видно, что величина продвижения воды в наклонных капиллярах больше, чем в предыдущем случае, т. е. в (8) и (9). Видно также, что подъём воды в вертикальном капилляре не зависит от угла наклона боковых капилляров. Но продвижение воды в левом ка- пилляре больше, чем в правом, на величину 2Δh1 .

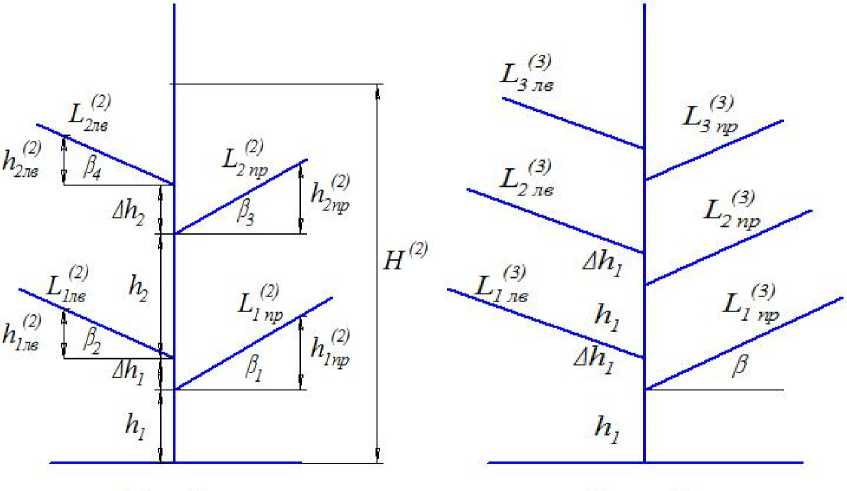
б

Рис. 4. Система несимметричных капилляров: а — двухуровневая; б — трёхуровневая

Более сложная система капилляров представлена на рис. 4, а . Она отличается добавлением капилляров второго уровня, расположенных на высоте h 2 над капиллярами первого уровня. Для элементов второго яруса введём обозначения:

• —    β 3 и β 4 — углы наклона правой и левой ветвей к горизонтали,

• —    ^пр и ^ ₂ 2_лв — высоты подъёма воды в капиллярах второго уровня,

  /(2 )          /(2 )

• —    ^{2 пр} и ^{2 лв} — расстояние продвижения воды в правом и левом капиллярах,

• — H ( 2 ) — общая высота подъёма воды в вертикальном капилляре в двухуровневой системе.

Для простоты положим h . = h₂, A h = Ah₂ и в 1 = в₂ = в₃ = в₄ = в ■ Тогда, используя те же рассуждения, что и выше, можно записать уравнения продвижения воды в каждой из капиллярных ветвей в виде:

Lnр sine = h - 5hl = h - 0,2h = hn ,(16)

L.в sine = h - hl f5 + 4J - 14 Ahl = h - 0,45hi - 0,25Ah1 = h.,(17)

44р sine = h -5hl - 14Ahl -3hl = h - 0,53hi - 0,25Ahi = h р,(18)

• L.B sine = h - 5hl - 4 Ahl - 3hl - 2 Ah = h - 0,53hl - 0,75Ah1 = h^,(l9)

H(2) = h + 2h + 2Ah -h | 4 + 4J- Ah | 4-4 | = h + 22h + 5Ah = h + l,47h + 1,25Ah ■(20)

• ^{( 2 )           1       11} ( 5 3 J ¹ ( 4 2 J        15 ¹ 4 ¹        ,    ¹    , ^l v у

• Для трёх уровневой системы (рис. 4, б) получаются следующие уравнения

L 13 nр sine =	h - 1 h = h - 0,143 h , 71                    1	(21)
L l 3 .в sine = h - 7 h l -	4A A = h - 0,143 h - 0,167A h , 6       1               ,          1        ,             1 ,	(22)
Z 23 nр sine = h - h l ^ 7 + 5	| - 4 A h = h - 0,343 h - 0,167A h , J 6     1             ,        1      ,           4,	(23)
L 2 3 лв sine = h - h l ^ 7 + 5 J-	A h | 4 + 4 | = h - 0,343 h - 0,417A h , 1 ( 6 4 J            ,        1      ,          4,	(24)
z 33 nр sine = h - h l ^ 7 + 5 + 3 J	- A h | 4 + 4 | = h - 0,678 h - 0,417A h , 1 ( 6 4 J            ,        1      ,          4,	(25)
L 3 3 л в sine = h - h l f 7 + 5 + 3 J-	A h | 4 + 4 + 4 | = h - 0,678 h - 0,917A h , 1 ( 6 4 2 J            ,        1      ,          4,	(26)

H(3) = h + 3h + 3Ah -h |4 +4 +41- Ah |4 +4 +41 = h + 2,322h + 2,083Ah .(27)

• (3)           1        11 (7 5 3 J 116 4 2 J ,      1    ,

Производя аналогичные расчёты при условии равенства углов наклона капиллярных ветвей, равенства расстояний между ветвями и вводя соответствующие обозначения для каждого из уровней, можно получить общее выражение для капиллярных систем с N уровнями:

L*U sine = h - hl 2 n,) 2^ - Ahl 2 (,) 2n=hnNP,.,(28)

HN)= h + Wh + NAh,-hl n,) J+. - ЛЛ,2 (N) 2n, где (N) — количество уровней в капиллярной системе, n — номер рассматриваемого уровня. Отсчёт уровней следует вести сверху вниз.

Полученные соотношения показывают, что в асимметричной капиллярной системе продвижение воды в ветвях верхних уровней меньше, чем в нижних. Но общая высота подъёма воды в вертикальном капилляре растёт. Так для двухуровневой капиллярной системы разность высот подъема составит

L p - L^в = ^J2                             (30)

И в общем виде можно записать

I ( N ) _ /( N ) _ л h V n ¹ L n пр L n лв = ^^h 1 ^ ( N ) 2 n ■

До сих пор рассматривали капиллярные системы, в которых количество ветвей в одном уровне не превышало двух. Определим, каким образом изменится распределение воды в капиллярах, если в одном уровне будет более двух ветвей (рис. 5).

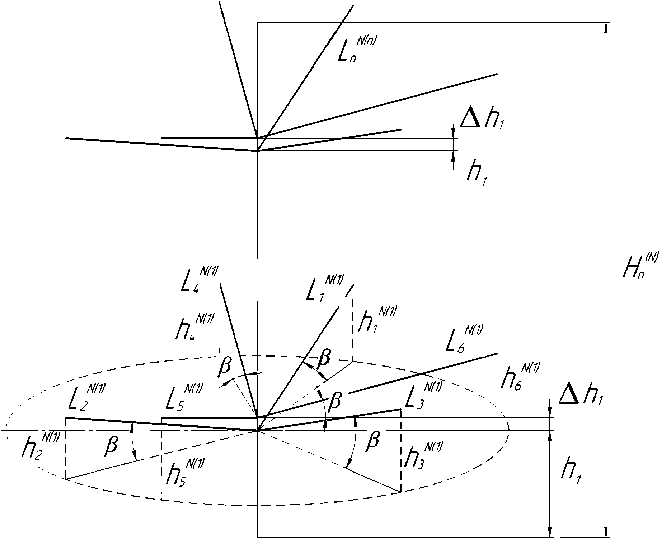
Рис. 5. Капиллярная система с тремя ветвями в каждом уровне

Допустим, что все капилляры имеют одинаковый радиус, равный r . Они присоединены к вертикальному капилляру того же радиуса на высоте h 1 от поверхности воды и наклонены под одним и тем же углом β к горизонтали. Обозначим величину продвижения воды в каждой из трёх наклонных ветвей через L * ¹ ) , L¹ , L 31 , а высоту подъёма воды в них соответственно через Ь^ , h ₂ ^{( 1 )} и h ₃ ^{( 1 )} . Высоту подъёма воды в вертикальном капилляре обозначим через H^ .

В принятых обозначениях уравнения для продвижения воды в капиллярных ветвях для такой системы (с учётом того, что L * ¹ ) = L , ¹ ) = L 3¹ ) ) могут быть записаны:

4 nr2h1pg + nrL12 3)Pg sin в = 2nracosa,(32)

4nr2h1pg + (H(1) - h1) nr2pg = 2nracosa .(33)

Тогда

L1‘(2.3) sine = h - 4h1,(34)

H"= h + h1 — 1 h1 = h + 4 h1-(35)

При равном радиусе капилляров на одном уровне может быть размещено не более трёх капилляров: 2π r /2 r = π. Допустим, что вторая группа капилляров размещена чуть выше первой (хотя бы на радиус капилляра) и смещена в пространстве так, что ветви не мешают друг другу. В этом случае капилляры находятся практически на одном уровне.

Введём для этой группы капилляров обозначения L41*, L1*, 41, то есть будем считать их тоже капиллярами первого уровня. Тогда уравнения продвижения воды в первом уровне капил- ляров можно записать следующим образом:

7 nr2h1pg + nr^ 3)рg sin в = 2nrocosa,(36)

7 nr2h1pg + 14 nr2Ah1pg + nrL*^ 6*pg sin в = 2nrocosa,(37)

7 nr2h1pg + 4 nr2Ah1pg + (h^ - h1 - Ah1) nr2pg = 2nrocosa .(38)

Откуда

411*2,3) sine = h - 7 h = h - 0,143hi,(39)

441*5,6* sine = h -7hi -4Ah1 = h -0,143h1 - 0,25Ah1,(40)

Hl* = h -1 h - 4 Ah + h + Ah = h + 6 h + 3Ah = h + 0,857h + 0,75Ah(41)

(i*           7 1 4 1      1         1           7 14 1             ,        1      ,         14 y

Не расписывая уравнений для двухуровневой системы капилляров с шестью капиллярами в каждом уровне (и далее до пятиуровневой системы), можно записать конечные результаты продвижения воды в этих системах. Так, например, для пятиуровневой системы они будут иметь вид:

L «* sine = h - 311 h = h - 0,032 h 1 ,	(42)
L 5^ . sine = h - — h - — A h = h - 0,032 h - 0,036A h , 4 ( 5,6*     r           31 1 28      1             ,         1       ,           1 ,	(43)
L 5 ' 2 , sine = h - h I + I - — A h = h - 0,072 h - 0,036A h , 4 ( 5 , 6* H          1 ( 31 25 J 28 1           , 1 ,          1 ,	(44)
L 5(2* , sine = h - h I — + — I - A h I — + — I = h - 0,072 h - 0,081A h , 4 ( 5 , 6 *                 1 ( 31 25 J       1 ( 28 22 J           ,      1 ,         1 ,	(45)
L 5 3 , sin e = h - h I — + — + — I - A h I — + — I = h - 0,125 h - 0,081A h 4 ( 5 , 6 *                 1 ( 31 25 19 J       1 ( 28 22 J           ,      1 ,        1	(46)
L 5 3 , sin e = h - h | — + — + — | - A h | — + — + — | = h - 0,125 h - 0,143A h , 4 ( 5 , 6 *                 1 ( 31 25 19 J       1 ( 28 22 16 J           , 1 ,         1 ,	(47)
L <4* sine = h - h 1 — + — + ± + 1- A h 1 — + — + — | = h - 0,202 h - 0,143A h , ч ( 2 ,з * н         1 1 31 25 19 13 J       1 1 28 22 16 J                 1             1	(48)

L ■ . sine = h - h I — + — + — + — I - A h I — + — + — + — I = h - 0,202 h - 0,243A h , (49)

• ^{4    ( 5} - ⁶*    ^{H        1} ( 31 25 19 13 J      ¹ ( 28 22 16 10 J                ^{1            1}

  L 4 &  ^sin^e = h ^— h i

  
  

  f i i i ii 1 f i i i ii 1 1111— A h 1111

( 3i 25 i9 i3 7 ) ⁱ ( 28 22 i6 i0 4 )

= h — 0,345 h _i — 0,493A h _i,

H sine = h + 5 h + 5A h — h ^f — + — + — + — + ^ 1 — A h ^f — + — + — + — + ! )

• ^{( 5 )                i i i} ( 3i 25 i9 i3 7 ) ⁱ ( 28 22 i6 i0 4 )

= h + 4,655 h _i + 4,507A h _i.

Общее выражение для величины продвижения воды в капиллярах разных уровней может быть записано для первой и второй тройки капилляров в каждом уровне в виде:

IN ^{( n} * sin R - h - h V ^{n i} - Л h V ^{n —i i}    - h^{N ( n} *                       f^Rt

Li (2,3) sinP = h hi L( N) 6n + i Ahi L( N) 6n _ 2 = hi (2,3) ,

IN ^{( n} * sinR- h - h V ⁿ __ ⁱ - Л h V ^{n —i i}    - h^{N ( n} *

L4 (5,6* sinP = h hi L( N * 6n + i Ahi L( N * 6n _ 2 = h4 (5,6* , а для высоты подъёма воды в вертикальном капилляре

H" = h + Nh + NAh — hT" —--AhY"'i^—.(55)

(N*            i i          (N*6n +1       i-^(N* 6n — 2

Если сравнить величины продвижения воды в ветвях и в вертикальных капиллярах последней системы с аналогичными, рассчитанными в предыдущих случаях, то можно увидеть следующее. Увеличение количества капиллярных ветвей в уровне и увеличение количества уровней приводят к увеличению продвижения воды в капиллярах нижних уровней и в вертикальном капилляре.

В последней 5-уровневой системе величина продвижения воды в первом уровне капилляров практически не отличается от высоты подъёма воды в отдельном вертикальном капилляре такого же радиуса. Одновременно с этим увеличивается подъём воды в вертикальном капилляре. Полагая k = 0,8, а Δ h ₁ = 0, из (55) можно определить высоту подъёма воды в вертикальном капилляре в одноуровневой системе, которая равна H (^ = i,685 h . То есть вода в вертикальном капилляре достигнет ветвей второго уровня на высоте 1,60 h . Эти ветви начнут заполняться водой, и произойдёт перераспределение сил в системе. Таким образом, увеличение количества ветвей в уровне также позволяет снять ограничения модели, описанной в [3], которую, тем не менее, необходимо использовать ввиду её простоты и наглядности.

Выводы. Насколько полученные в настоящей работе результаты применимы к реальным растениям, можно показать на примере пихты Нордмана . Внизу вокруг ствола на одном уровне расположены 5–6 наиболее длинных ветвей. Они занимают в основании почти всю окружность ствола. Чуть выше этих ветвей (на величину Δ h , примерно равную диаметру этих ветвей) в одном уровне расположены ещё 3–4 ветви такого же диаметра и длины. Ветви этого ряда по вертикали располагаются «между» нижними. Таким образом обеспечивается доступ света в нижний ярус. Скелетные ветви последующих уровней расположены по отношению друг к другу на расстоянии h i , много большем Δ h . Длина ветвей в этих уровнях тем меньше, чем больше номер уровня. В промежутках между уровнями скелетных ветвей на стволе имеются короткие, несимметричные отростки и отдельные веточки (не образующие скелетных ветвей). Возможно, одна из их функций — обеспечение подъёма воды в капиллярной сети ксилемы до уровня ближайшей вышележащей скелетной ветви. Пихта Нордмана имеет пирамидальную форму. Наличие асимметричных элементов в ветвящихся капиллярных системах с капиллярами одинакового радиуса не противоречит выявленным в работе [3] закономерностям распределения воды в ветвящихся симметричных капиллярных системах. Описанные в [3] закономерности применимы и к несимметричным системам. Эти закономерности можно рассматривать как универсальные для мира растений.