Проектирование дозирующих заслонок двухдискового рассеивателя минеральных удобрений и семян сельскохозяйственных культур по условию постоянства характеристик угла бросания

Введение. Равномерное распределение минеральных удобрений по поверхности поля позволяет добиться увеличения урожайности и повышения его качества, а применение дифференцированных способов внесения удобрений позволяет еще и снизить затраты на нерациональное использование удобрений. В последние годы в сельском хозяйстве все чаще используются машины для внесения минеральных удобрений, а также для посева семян сельскохозяйственных культур с применением систем глобального позиционирования, однако, чтобы использовать данные системы, необходимо спроектировать дозирующие устройства так, чтобы при изменении дозы внесения удобрений или семян не ухудшалось качество распределения. Это означает неизменность величины и положения сектора рассева при любой подаче удобрений на диск.

Дозирование расхода у навесных распределителей удобрений выполняют двумя заслонками, расположенными концентрично распределяющему диску. Поворотом заслонок относительно оси диска регулируют подачу удобрений на диск. Форма прорезей в заслонках имеет существенное значение для получения качественного распределения удобрений. Правильным выбором формы дозирующих отверстий можно одновременно регулировать как расход, так и радиус подачи удобрений на центробежный диск.

Методика исследования. Целью исследований является разработка такого способа построения прорезей дозирующих заслонок, чтобы при регулировке расхода обеспечивалось постоянство математического ожидания и среднеквадратического отклонения угла бросания.

Моделированием распределения удобрений двухдисковым аппаратом установлено, что для равномерного распределения удобрений по середине поло сы рассева необходимо иметь Ma = 0,6 рад и ста = 0,6 рад. [1,2, 3, 4, 9].

Угол схода wti является функцией радиуса подачи го. Для радиальной лопатки уравнение имеет вид:

cos га , 2R cat =------In---------------.      (1)

1-8ІП(9 ГО(1 + 8ІП(3)

Рассмотрим угол а как функцию случайных аргументов Го и Л.

. cos гр , 2R „ ос — X и--In--и Ө, (2)

l-sin

где углы отсчитываются от поперечной оси координат в направлении вращения диска. Ma = 0,6 рад, если отсчет угла вести по наименьшему расстоянию от линии движения. Если отсчет угла ведется от вектора скорости машины, то Ma = тт—06, то есть 2,54 рад.

Заданное постоянное значение угла бросания a можно получить только при определенных сочетаниях аргументов, определяемых по уравнению, которое после подстановки и преобразования имеет вид:

, х 2R         .,о,

г(ос) =------ехр(-------—-. w

• 1    + sin^cos^

Последнее уравнение в полярных координатах г, Л дает логарифмическую спираль [5] вида р = аехр (кА), где а и к - параметры спирали, определяемые по зависимостям:

2R       1-sin^

a =---- ;— ехр(-- (ос - Ө)),

• 1    + sin^ cos^             (4)

,       „ l-sine5

k = ctgd =------ cos^

Подача удобрений в любую точку спирали дает заданное постоянное значение угла а. Форма спирали зависит только от угла трения частиц по лопаткам, а ее расположение - от ср, а и R (рисунок 1).

Рисунок 1 - Спирали точек подачи, обеспечивающих получение заданных углов бросания: (3; 3,3...5,2) радиан

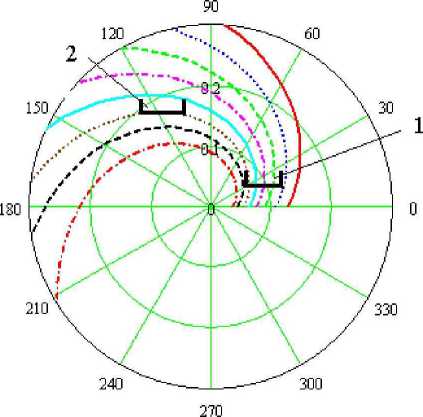
По рисунку 1 видно влияние расположения ту-конаправителя на величину угла рассева. Туконапра-витель 1 пересекает несколько спиралей, поэтому сектор рассева будет больше, чем при туконаправителе 2, который расположен на одной спирали.

Регулирование угла бросания наиболее эффективно при перемещении туконаправителя в направлении нормали к спирали. Так, при положении туконаправителя в позиции 1 (рисунок 1) более эффективно поперечное смещение туконаправителя, а в позиции 2 - продольное.

Задача выбора положения места подачи должна рассматриваться с позиций обеспечения заданного значения математического ожидания угла бросания и ст = 0,834-6,056-г+ 15,146-г2+0,167-2 + 0,040^

Графики функции ст^г, Q) представлены на рисунке 2. Значение a_a = 0,6 рад при изменении расхода в пределах 0,4-1,5 кг/с достигается регулировкой радиуса подачи в пределах 0,06-0,113 м.

Расширение сектора рассева удобрений при внесении малых норм можно получить применением лопаток, наклоненных вперед, или подачей удобрений через два тукопровода, смещенных по углу подачи на угол до 80 градусов. Сужение сектора рассева при больших нормах высева можно получить применением лопаток, отклоненных назад [7, 8].

оптимального значения его среднего квадратического отклонения.

Результаты исследований и их обсуждение. Среднее квадратическое отклонение угла бросания для двухдискового аппарата принято 0,6 радиана. Так как среднее квадратическое отклонение угла бросания зависит от радиуса подачи и расхода удобрений через аппарат, то возникает вопрос, какими способами можно поддерживать его значение в указанных пределах. При постоянном радиусе подачи с увеличением расхода угол сектора рассева увеличивается.

Для диска диаметром D = 500 мм с радиальными лопатками эмпирическая зависимость среднего квадратического отклонения от радиуса подачи и расхода определена формулой [6,10]:

Постоянство математического ожидания угла бросания будет выполнено, если середина прорези совпадает со спиралью равных углов схода, построенной по зависимостям (3), (4). Спираль надо построить при заданных значениях радиуса диска, угла трения, угла Ө (рисунок 3). Угол Ө между радиусом и касательной к первой спирали следует определять по зависимости

„         І-sincz и = arcctg----------.           (6)

cosa               ’ '

cra(r,Q) := 0.834 - 6.056-Г + 15.146-Г2+ 0.167-Q + 0.040-T-Q           Г := 0.01,0.02.. 0.15

В := 29    V:= 2 qmin := 0.005          Q := В-0.5-V-qmin Q = 0.145

q1 := 0.05 QI := B-0.5-V-q1 Q1 = 1.45

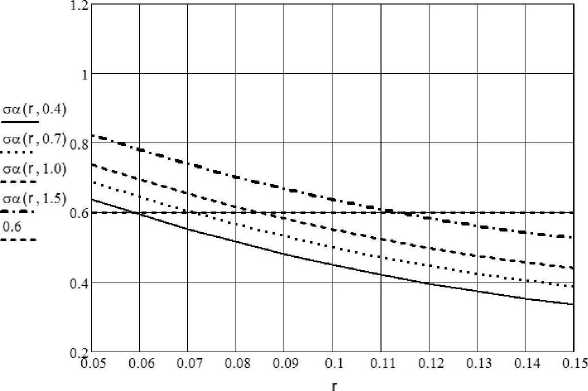
Рисунок 2 - Графики функции oa(r, Q) при изменении радиуса подачи от 0,05 до 0,15 м и расхода от 0,4 до 1,5 кг/с

При ф = л / 6 угол Ө равен 60°. Угол между спиралью второй заслонки должен быть на 90° меньше, то есть -30°. Спираль второй заслонки должна быть левой, её коэффициент к должен быть отрица тельным. Построенные таким образом спирали пересекаются под углом 90°, что и требуется.

Координаты X, Y точек спиралей вычислены в системе Mathcad и вставлены в документ графического редактора для построения спиралей по точкам (рисунки 3 и 4).

Ф > - R := 028 Ма := 2.54

Ө1 := acot(k) Ө13 := Ө1-- ’ '                   =                  TV

1 - sitl/Ф)

9 > 1 k ?--— k = 0 J 77 соз(Ф)

01g = 60     02 - ^ - 01

02 = 0.524

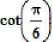
X2 := -тг,(^д + 01)„ тг

p(X2,k) :=  --^—- expf— --^ (Ma- 9)1 exp(k-X2) 1 + ЗШ^Ф) СОз(Ф)

p(X2,0J77)

p(X2.- 1.732)

X2

Рисунок 3 - Построение ортогональных спиралей при проектировании прорезей заслонок

Для постоянства среднего квадратического отклонения угла бросания по рисунку 2 или по уравнению (5) (рисунок 5) определяем соответствие между расходом и радиусом подачи при постоянном а_а. Далее используем теоретическую или эмпирическую зависимость между расходом и диаметром дозирующего отверстия. В примере расчета (рисунок 5) принята гидравлическая форма истечения при коэффициенте истечения Л_11с,_г1 = 0,3, тогда определена скорость истечения

V =Я • J^gh, (7) и расход удобрений -

Q = vucm- Р"^-- (8)

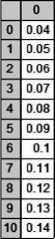
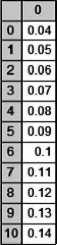
С помощью зависимостей (7) и (8) определены диаметры дозирующих отверстий для получения расхода, заданного вектором Q.

Далее в графическом редакторе вычерчена спираль равных углов бросания (рисунок 6) и сетка полярных координат. В точках пересечения спирали с окружностями радиусов д проводим окружности диа метров ф. Значения д, 4 берем как элементы векторов из рисунка 5. Используя кривую Безье, соединяем касательно вершины построенных окружностей первой (рисунок 5) и второй (рисунок 6) заслонок, а внутреннюю область удаляем.

Вторая заслонка должна иметь прорезь, у которой сохранена такая же, как на рисунке 5, зависимость между радиусом и диаметром отверстия, но форма спирали должна быть левой и ортогональной первой спирали.

Полученные дозирующие заслонки в системе КОМПАС-ЗО совмещаем, используя функцию поворота, второе дозирующие отверстие поворачиваем относительно центра заслонки до совпадения крайних кромок дозирующих отверстий первой и второй заслонки. Таким образом определяем сектор поворота заслонок от закрытого положения до максимального расхода туков, который составляет 215°

При выполнении этих условий дозирующее отверстие, образованное пересечением прорезей, близко к квадрату (рисунок 7), а вписанная в него окружность близка к расчетной для заданного расхода.

2 Һ := 1       f(r) := 0.834- 6.056r + 15.146г + 0.167Q + (0.040r-Q Q(r) := rootffo.834- 6.056r + 15.146r2 + 0.167Q + (0.040r-Q) - 0.8 Q(0.12) = 2.763      i: 0.. 10 r := 0.04+ i-0.01     g:=9.81											- 0.8 ,Q,1.0,4|
Q. : Q r 1            1	;         p		:= 1000	i := 0.. 10		d.:= i		4-Qj 0.3-p -Tr-^2gh
Q =		0	r =		0	d -			0
	0	1.091		0	0.04		0		0.032
	1	1.366		1	0.05		1		0.036
	2	1.622		2	0.06		2		0.039
	3	1.859		3	0.07		3		0.042
	4	2.077		4	0.08		4		0.045
	5	2.276		5	0.09		5		0.047
	6	2.457		6	0.1		6		0.049
	7	2.619		7	0.11		7		0.05
	8	2.763		8	0.12		8		0.051
	9	2.888		9	0.13		9		0.053
	10	2.995		10	0.14		10		0.054

Рисунок 4 - Расчет радиуса подачи и диаметра дозирующего отверстия в системе Mathcad

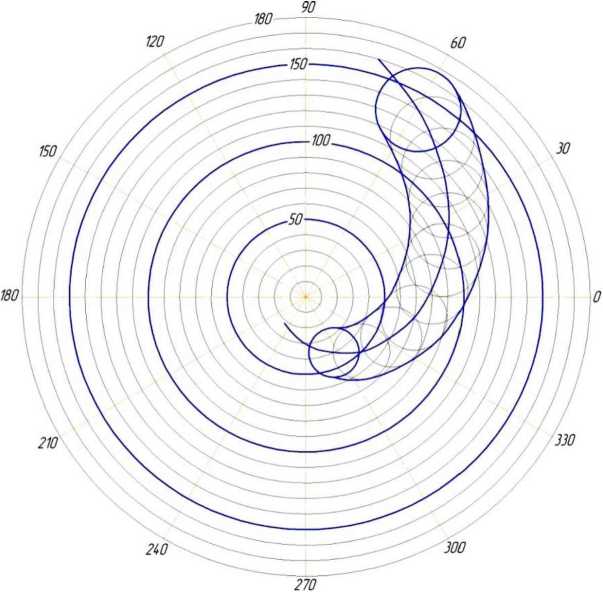
Рисунок 5 - Построение прорези первой дозирующей заслонки

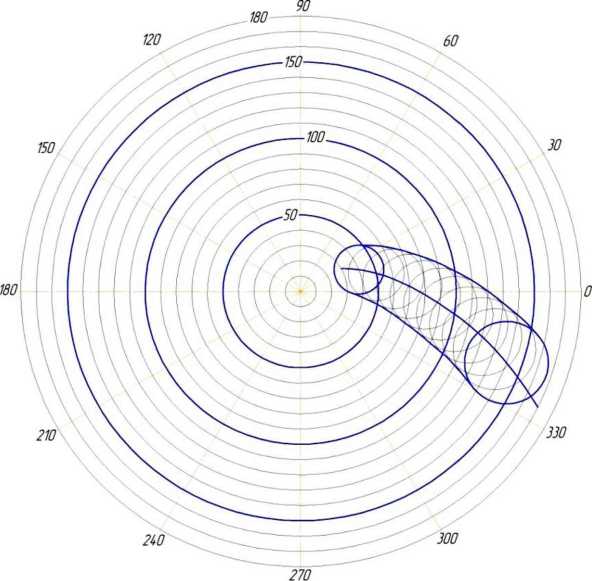
Рисунок 6 - Построение левой прорези второй дозирующей заслонки

	0
0	1.091
1	1.366
2	1.622
3	1.859
4	2.077
5	2.276
6	2.457
7	2.619
8	2.763 ;
9	2.888
10	2.995

	0
0	1.091
1	1.366
2	1.6221
3	1.859
4	2.077
5	2.276
6	2.457 |
7	2.619
8	2.763 |
9	2.888
10	2.995

	0
0	0.032
1	0.036
2	0.039
3	0.042
4	0.045
5	0.047
6	0.049
7	0.05
8	0.051
9	0.053
10	0.054

	0
0	0.032
1	0.036
2	0.039
3	0.042
4	0.045
5	0.047
6	0.049
7	0.05
8	0.051
9	0.053
10	0.054

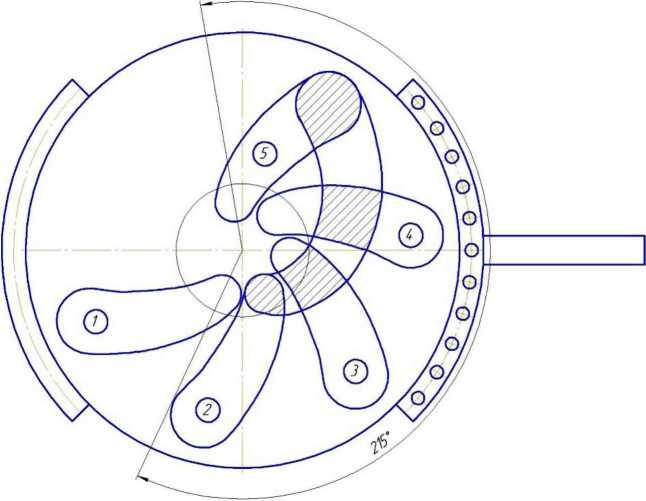
1, 2, 3, 4, 5 - положения дозирующей заслонки

Рисунок 7 - Форма дозирующего отверстия при различных углах поворота второй заслонки

Регулировка дозы внесения одного вида удобрений не требует необходимости регулирования положения сектора рассева. Однако при изменении вида удобрений меняется угол трения, а это приводит к изменению угла схода частиц.

Коэффициенты трения большинства удобрений по стали находятся в пределах 0,5-0,6. Но гранулированная мочевина имеет минимальный коэффициент трения 0,31, а порошковидный суперфосфат - максимальный 0,71.

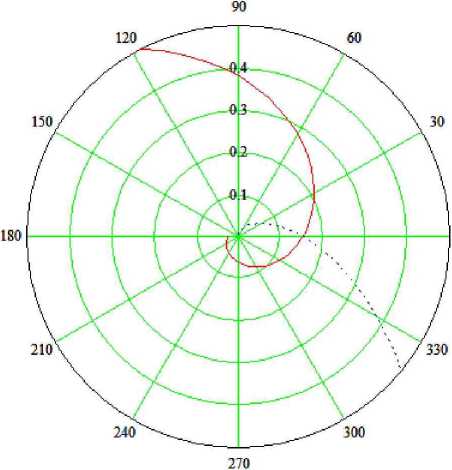
Из рисунка 8 видно, что при минимальном радиусе подачи переход от внесения мочевины к распределению порошковидного суперфосфата потребует изменения угла Л на 1,2 радиана. Поэтому при проектировании дозатора необходимо предусмотреть поворот одновременно двух заслонок на 1,2 радиана для получения Ма = ±0,6 рад при внесении суперфосфата и карбамида. При больших радиусах подачи положение сектора рассева менее чувствительно к изменению угла трения. Однако применение больших радиусов подачи связано с увеличением числа частиц, хаотически покидающих диск от первичного удара в зоне подачи, что приводит к неравномерному распределению удобрений по поверхности поля и образованию пики в области работы центробежных дисков.

Х:=0

ф:= 0.3,0.31.. 0.6

,          .    „ cos| ф' , Г 2-R

Мех ф,го, := X + Ө + ----^—-In — ------——

1 - sin| фі го-1 1 + sin' Ф' I

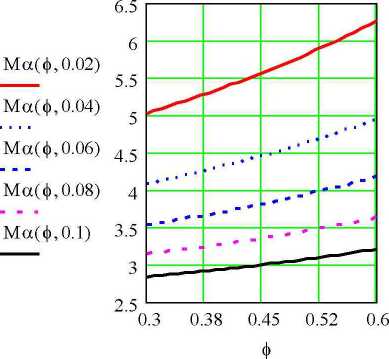
Рисунок 8 - Г рафик зависимости математического ожидания угла бросания от угла трения и радиуса подачи

Выводы

• 1.    В результате проектирования дозатора центробежного распределителя было установлено, что середины дозирующих заслонок целесообразно выполнять по спиралям, одна из которых является геометрическим местом точек подачи, дающих постоянный угол бросания, и фиксируется на неподвижном секторе, а вторая пересекает первую под углом 90° и фиксируется на секторе первой заслонки. Ширину дозирующих щелей рекомендуется рассчитать по условию постоянства среднего квадратического отклонения угла метания.

• 2.    Спроектированная конструкция дозатора центробежного рассеивателя позволяет уменьшить количество регулировок, повысить качество распределения минеральных удобрений и семян сельскохозяйственных культур, а также дает возможность его использования для дифференцированного внесения минеральных удобрений, так как изменение регулировки дозы внесения удобрений не приводит к изменению равномерности рассева.

• 3.    На этапе проектирования дозатора необходимо предусмотреть возможность одновременного поворота двух дозирующих заслонок - это позволит регулировать сектор распределения удобрений или семян сельскохозяйственных культур при смене вида семян или удобрений, которые отличаются коэффициентом трения.