Проектирование, изготовление и механические испытания ячеистых структур на основе трижды периодической минимальной поверхности

Аддитивное производство и прототипирование, в частности 3D-печать, в настоящее время перешли из разряда инновационных в повсеместно применяемые технологии для изготовления сложных элементов конструкций в различных областях промышленности [1]. При этом в последние десятилетия продолжается прогресс и совершенствование оборудования для аддитивного производства и 3D-печати. Разнообразие техноло-

гий формирования изделий, точность изготовления, геометрические особенности в виде сложной и индивидуальной формы, соблюдение, повторяемость и контроль технологических параметров и режимов «выращивания» позволяет говорить о широких возможных областях применения аддитивных технологий в автомобилестроении, общем машиностроении, авиа-, ракетостроении, химической промышленности, медицине и других [2–9].

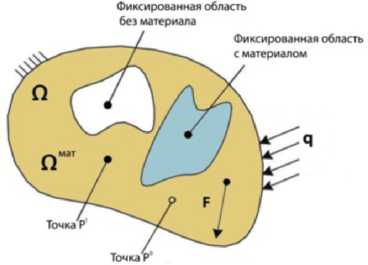
Одной из особенностей изготовления элементов конструкций методом аддитивных технологий является возможность создания изделий со сложной геометрической формой и пространственно-распределенной 3D-архитектурой. Такие геоме- трические формы невозможно получить традиционными субтрактивными методами производства [10]. Сюда можно отнести изготовление изделий, проектируемых с применением алгоритмов топологической оптимизации (рисунок 1) [11] и периодических (непериодических) ячеистых структур (рисунок 2) [12].

поглощения (абсорбации) энергии (ударных нагрузок), ударопрочность, звукопоглощение и теплообменные свойства [15–25]. Развитие аддитивных технологий позволяет использовать данные ячеистые структуры в различных инженерных задачах. Например, при проектировании несущих элементов конструкций с заполнением ячеисты-

Схема

Исходная деталь

Деталь после оптимизации

а

Рисунок 1. Топологическая оптимизация конструкции

б

в

г

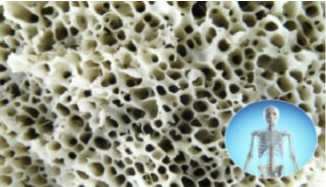
Рисунок 2. Ячеистые структуры в природе: а – пчелиные соты; б – крылья бабочки; в – человеческая кость; г – морская звезда

Ячеистые структуры широко встречаются в природе и являются источником вдохновения для исследований во многих направлениях (рисунок 2) [13]. Получаемые результаты исследований можно использовать для новых инженерных решений при проектировании в различных областях.

Ячеистые структуры можно рассматривать как потенциальную возможность для замены сплошного объема в элементе конструкции с целью снижения его массы, расхода дорогостоящих материалов при сохранении функциональных и эксплуатационных характеристик (рисунок 3) [14].

Ячеистые структуры обладают определенными уникальными свойствами. К ним можно отнести легкий вес, высокую удельную жесткость и прочность, что очень важно при создании авиационной и космической техники, отличные характеристики ми структурами или создании функциональных композитных материалов с периодическими ячеистыми структурами и настраиваемыми физикомеханическими свойствами [26–31].

Особую роль рассматриваемые ячеистые структуры имеют для аэрокосмической отрасли. Их применение в элементах конструкций космических аппаратов (КА) позволит решать задачи снижения веса при сохранении жесткостных и прочностных показателей, поскольку ячеистые структуры обладают широкими возможностями управления их относительной плотностью. Благодаря особенному характеру деформирования ячеистые структуры могут использоваться при создании функциональных материалов и деталей для поглощения ударных и снижения вибрационных нагрузок, акустического воздействия. Кроме

I/ I — ОСМИЧЕСКИЕ АППАРАТЫ VI ТЕХНОЛОГИИ нш

Том 8

Закрытая пена              Открытая пена                  Соты               Ферменная структура

Рисунок 3. Ячеистые структуры для элементов конструкций

того, перспективным инженерным решением яв-       1. Геометрическое моделирование

172 ляется использование изучаемых ячеистых струк- TPMS тур в системах терморегулирования КА (тепло-

обменники, радиаторы) за счет высоких удельных

Минимальная поверхность – это поверхность,

поверхностных характеристик.

В связи с перечисленными особенностями

для которой средняя кривизна H = ( k 1 + k ₂)/2 равна нулю в каждой точке и, соответственно, k 1 = - k ₂,

становится интересным применение ячеистых структур на основе трижды периодических минимальных поверхностей (Triply Periodic Minimal Surfaces - TPMS). Для реализации функционального проектирования новых материалов и конструкций с заданными свойствами на основе TPMS необходимо системное понимание особенностей деформирования, механизма и характера разрушения данных ячеистых структур. В основе этого лежит информация о механических свойствах, таких как модуль упругости, предел прочности при растяжении/сжатии и других. Для оценки механических свойств, а также их зависимости от геометрических и технологических параметров необходимы экспериментальные исследования образцов ячеистых структур, изготовленных аддитивным методом [32–33].

В данной статье рассматриваются вопросы геометрического моделирования, изготовления методом 3D-печати и проведения экспериментальных исследований образцов периодических ячеистых структур на основе трижды периодических минимальных поверхностей.

Целью статьи является исследование механических свойств образцов, изготовленных методами фотополимерной 3D-печати для выбранных двух типов ячеек TPMS с различными значениями относительной плотности. Полученные результаты позволят оценить зависимость геометрических и технологических параметров на характер деформирования и прочностные свойства изготовленных образцов.

где k ₁ и k ₂ - главные кривизны в двух взаимно ортогональных плоскостях. Минимальные поверхности, такие как катеноид и геликоид, были открыты и описаны в XVIII веке. В XIX веке Герман Шварц описал периодические минимальные поверхности Schwarz's Primitive (далее Primitive) и Schwarz's Diamond (далее Diamond), обладающие кубической симметрией. В 1970 году Alan Hugh Schoen - американский физик, исследователь, сотрудник NASA, описал 12 новых TPMS, основанных на графических схемах кристаллических решёток, таких как Gyroid и I-WP [34]. На рисунке 4 представлены TPMS, рассматриваемые в данной статье.

Трехмерные координаты минимальной поверхности TPMS могут быть определены как вещественные части следующих комплексных интегралов, согласно параметризации Эннепера-Вейерштрасса:

x = Re e i ’

k

j ( i - T ) 2 F ( T ) d T'

“ 0                     J

(   “

y = Re ei j

^k “ 0

A

i ( i + T)2 F ( T ) dT J

“ z=Re ei ’ jTF(T) dT, k “0           J

где i ² = -1; т =t a +t b ; 0 - угол Бонне; F (т) = = (1–14τ⁴+τ⁸)^-1/2 – функция Вейерш т ра с са.

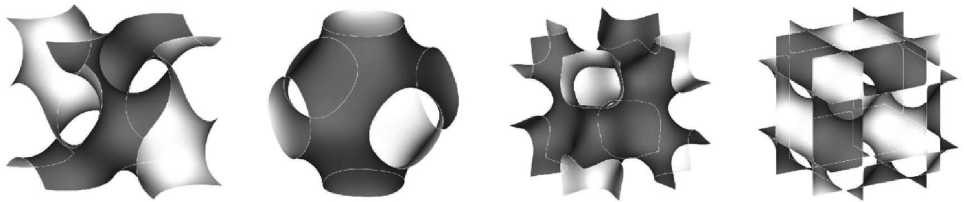
Gyroid             Primitive              I-WP             Diamond

Рисунок 4. Трижды параметрические минимальные поверхности

Проектирование, изготовление и механические испытания ячеистых структур…

Из-за сложности вычислений данных комплексных интегралов функции для описания топологий TPMS можно с достаточной точностью аппроксимировать с использованием ряда Фурье [35]. При этом надо понимать, что средняя кривизна H = 0 получаемых поверхностей будет достигаться при увеличении количества членов ряда, аппроксимирующих минимальную поверхность TPMS:

F ( r ) = z [ A n ⁽ r ) cos ^{f 2 n} r n ^{+ 9} n j , ⁿ I I L ))

где A_n ( r ) – амплитуда n -ой ячейки; 2π· n / L – частота и размер элементарной ячейки; θ _n – начальная фаза; r – радиус-вектор.

Применение ряда Фурье позволяет получить неявную функцию F ( x , y , z ) = 0 от трех переменных [36]. Данная функция образует поверхность, которая разделяет область элементарной кубической ячейки на два подпространства, лежащие внутри или снаружи поверхности. Рассматриваемые в статье ячейки минимал ь н ы х поверхностей могут быть описаны в первом п орядке аппроксимации следующими уравнениями:

FG ( xy , z ) = cos ( 2 . X ) Sin ^{( 2 n Y )+}              (1)

+ cos ( 2 n Y ) sin ( 2 n Z ) + cos ( 2 n Z ) sin ( 2 п X ) = 0,

F P ( x , y , z ) = cos ( 2 пX ) + cos ( 2nY ) + cos ( 2 nZ ) = 0, (2)

F D ( x , y , z ) = cos ( 2 пX ) cos ( 2nY ) cos ( 2 nZ ) — - sin ( 2 пX ) sin ( 2nY ) sin ( 2nZ ) = 0,

FI WP ^{( x} . y . ^z

f cos ( ^{2 n} X ) cos ⁽ 2.Y ⁾⁺ j ) = ² ₊ cos (...) cos ⁽ 2.Z ^{) +}

■ ^cos ( ^{2 n Z} ) ^{cos ( 2 n X} ) J

—

—(cos( 4nX) + cos(4nY) + cos(4nZ )) = 0,

X = xn x/ L x , Y = yn_y/L_y , Z = znz/L z , где F_G – ячейка типа Gyroid; F_P – ячейка типа Primitive, F_D – ячейка типа Diamand; F_IWP – ячейка типа I-WP; L_x , L_y , L_z – проектируемые размеры ячейки в трех осевых направлениях, n_x , n_y , n_z – количество повторений ячейки вдоль осей координат.

Для создания ячеистых структур применялось программное обеспечение MSLattice Software, разработанное Oraib Al-Ketan из Нью-Йоркского университета Абу-Даби в сотрудничестве с Rashid Abu Al-Rub из Халифского университета науки и технологий [37]. MSLattice позволяет генерировать различные типы ячеек и может сохранять получаемые результаты в файлы формата STL, необходимые для изготовления ячеистых структур с использованием аддитивного производства. Программное обеспечение позволяет пользователю создавать однородные, а также функционально градиентные ячеистые структуры на основании выбранного вида известных ячеек TPMS. Также пользователь может задавать и строить собственные топологии ячеек на основе неявных функций и экспортировать соответствующие результаты в CAD/CAE-системы.

В качестве примера рассмотрим результат построения элементарной ячейки и ячеистой структуры типа Primitive на основе уравнения (2). Непосредственно уравнение F_P ( x , y , z ) = 0 позволяет построить поверхность нулевой толщины (рисунок 5). Однако если добавить в правую часть уравнения параметр t и составить неравенство t ≤ F_P ( x , y , z ) ≤ t , то можно построить ячейку в виде оболочки. Аналогично строится ячейка в виде сплошного тела согласно неравенству F_P ( x , y , z ) ≤ t . Таким образом, параметр t в сочетании с уравнениями (1)-(4) отвечает за объемную долю материала в ячейке.

-t < F_PX У, ⁼)            -0,3 < F_P(x, y, z) < 0,3

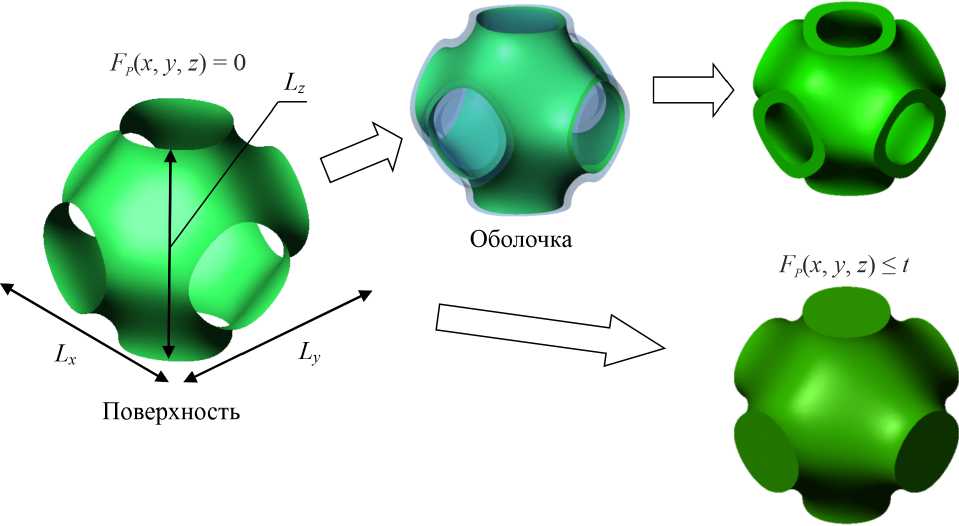
Тело

Рисунок 5. Ячейка типа Primitive в виде поверхности, оболочки и тела

Примеры ячеек

Таблица 1

Тип ячейки Форма ячейки Поверхность Оболочка Тело Gyroid «□Г ’ -М 44 * t = 0 t = ±0,25 ф t = 0,25 Primitive t = 0 о t = ±0,2 45 ла      К t = 0,2 и |_ ОСМИНЕСКИЕ АППАРАТЫ VI технологии к^нв

На рисунке 6 представлена ячейка размерами L_x = L_y = L_z = 5 мм, а также ячеистая структура, построенная на основе данной ячейки с количеством повторений ячеек n_x = n_y = n_z = 4. Таким образом, размеры ячеистой структуры составили 20×20×20 мм. Относительная плотность ячеистой структуры определяется как отношение объема материала в ячейке V к объему габарита ячейки:

V р =------X 100%, LLL xyz

¹⁷⁴ где V – объем, ограниченный поверхностью TPMS и границами ячейки при | x | ≤ L_x /2, | y | ≤ L_y /2, | z | ≤ L_z /2. Относительная плотность структуры на рисунке 6 составила 28,55 %.

Том 8

В таблице 1 представлены примеры ячеек, созданных на основе уравнений (1)-(4). Данные топологии элементарной ячейки могут служить для создания как периодических ячеистых структур с заданными размерами, так и пористой структуры различных конструктивных элементов.

2. Создание образцов TPMS типа Gyroid и I-WP

На основе вышеизложенных подходов были заданы уравнения и параметры для моделирования экспериментальных образцов ячеистых структур типа Gyroid и I-WP. Образцы имели квадратное поперечное сечение размером 40x40 мм и высоту 60 мм соразмерно оснастке испытательной машины.

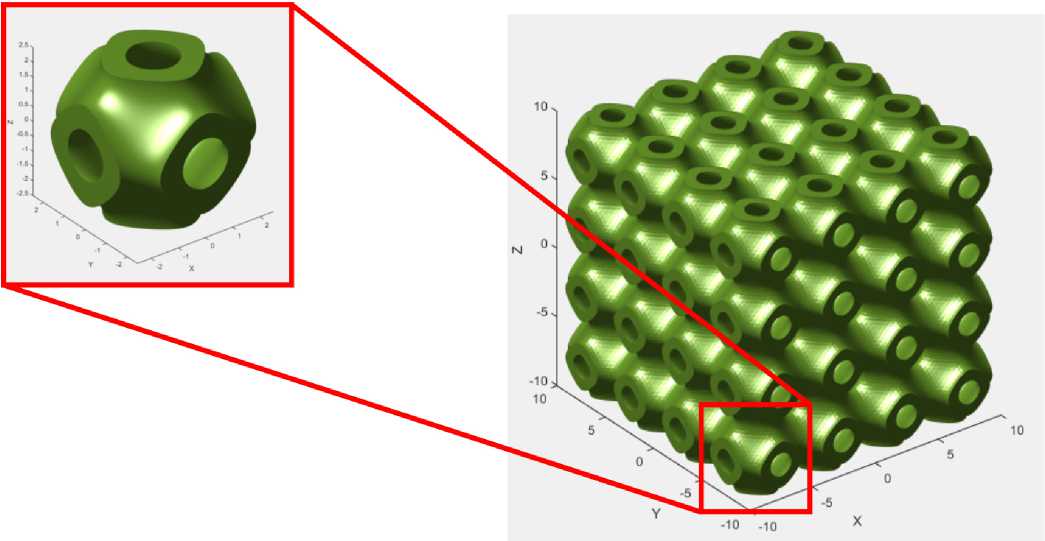
Рисунок 6. Элементарная ячейка типа Primitive и периодическая ячеистая структура

Окончание таблицы 1

Тип ячейки

Поверхность

Форма ячейки Оболочка

Тело

I-WP

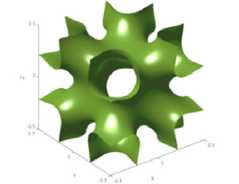
t = 0

t = ±0,75

t = 0,75

Diamond

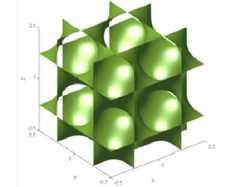
t = 0

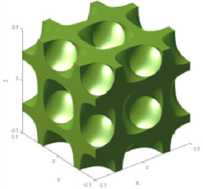
t = ±0,25

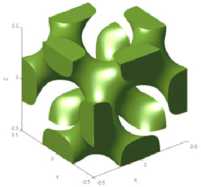
t = 0,25

Для создания ячеистых структур в виде оболочки типа Gyroid на основе уравнения (1) были выбраны размеры элементарной ячейки L_x = L_y = L_z = 10 мм и различные значения параметра t = {0,55; 0,65; 0,75; 0,85}. Количество повторений элементарных ячеек в соответствующих направлениях по осям было равно: n_x = n_y = 4, n_z = 6. Полученные 3D-модели ячеистых структур типа Gyroid с заданными параметрами представлены в таблице 2.

Для создания ячеистых структур в виде оболочки типа I-WP на основе уравнения (4) были выбраны размеры элементарной ячейки L_x = L_y = L_z = 10 мм и различные значения параметра t = {1,6; 1,8; 2,0}. Количество повторений элементарных ячеек в соответствующих направ-

лениях по осям было равно: n_x = n_y = 4, n_z = 6. Полученные 3D-модели ячеистых структур типа I-WP с заданными параметрами представлены в таблице 3.

Трехмерные модели, сгенерированные в MSLattice, сохранялись в файлы с формата STL и экспортировались в CAD-систему трехмерного моделирования. Для исключения краевого эффекта при механических испытаниях к моделям образцов были добавлены сверху и снизу сплошные площадки толщиной 4 мм, после чего данные модели были переданы в препроцессор для подготовки к 3D-печати.

Образцы были изготовлены по технологии трехмерной фотополимерной печати из смолы Anycubic ABS-Like Resin Pro 2 на 3D-принтере

3D-модели образцов типа Gyroid

Таблица 2

Образец	GYR 55	GYR 65	GYR 75	GYR 85
Параметр t	0,55	0,65	0,75	0,85
Относительная плот-ность,%	34,67	41,77	48,84	55,96
Толщина стенки, мм	1,194–1,292	1,51–1,61	1,999–1,92	2,027–2,143
3D-модель		^.'     DEEL]	Bill	r^fc^U K^^h^^j

If ОСМИЧЕСКИЕ АППАРАТЫ И технологии aesas

Том 8

модели Anycubic Photon Mono Pro 4K. Толщина слоя печати составляла 50 мкм, время отверждения слоя – 2,5 с.

3. Механические испытания образцов материала

В проводимом авторами исследовании одной из перспективных задач является создание численных конечно-элементных моделей деформирования рассматриваемых ячеистых структур. Для корректного сравнения испытаний с численными расчетами необходимо иметь достоверные данные о механических свойствах материала, из которых изготовлены образцы. Поэтому для определения характеристик механических свойств материала ячеистых структур были проведены испытания стандартных образцов на растяжение и сжатие, выполненных из применяемой смолы Anycubic ABS-Like Resin Pro 2. Испытания выполнялись на основе методик, представленных в ГОСТ 11262–2017 «Пластмассы. Метод испытания на растяжение», ГОСТ 4651–2014 «Пластмассы. Метод испытания на сжатие», ASTM D 638 «Standard Test Method for Tensile Properties of Plastics» и ASTM D 695 «Standard Test Method for Compressive Properties of Rigid Plastics».

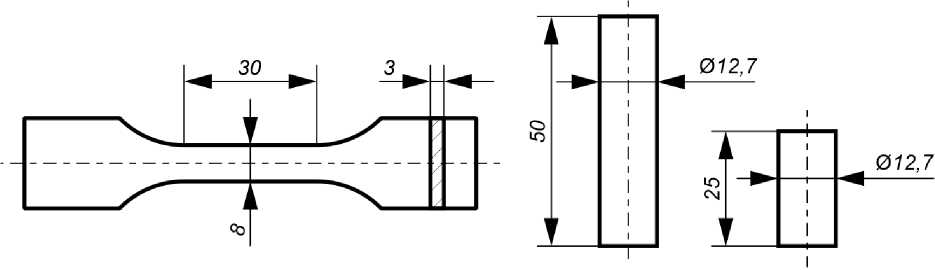
Чтобы обеспечить сходство механических свойств стандартных образцов, параметры печати устанавливались такими же, как и для печати образцов ячеистых структур. При печати образцы были сориентированы вертикально, т.е. перпендикулярно платформе 3D-принтера, вдоль направления ее движения. Плоские образцы на растяжение имели форму лопатки в захватной части (рисунок 7а). Образцы на сжатие имели форму цилиндра и изготавливались в двух вариантах: длинный – для определения модуля упругости (рисунок 7б), короткий – для определения предела прочности (рисунок 7в).

Испытания проводились в Инженерноиспытательном центре ФИЦ ИВТ на универсальной испытательной машине Tinius Olsen 100ST. Для испытаний на растяжение применялись клиновидные захваты (рисунок 8а), а для испытаний на сжатие – плоские пуансоны (рисунок 8б). Продольные деформации измерялись с помощью бесконтактного видеоэкстензометра по соответствующим меткам, которые наносились на рабочую часть образцов (рисунок 8в). Для измерения коэффициента Пуассона при растяжении на плоские образцы наклеивалось по два тензорезистора под углом 90°, по которым определялось отношение поперечных деформаций к продольным (рисунок 8г).

б

а

в

Рисунок 7. Образцы для испытаний: а – на растяжение; б, в – на сжатие

Таблица 3

3D-модели образцов типа I-WP

Образец	IWP16	IWP18	IWP20
Параметр t	1,6	1,8	2,0
Относительная плотность, %	42,27	48,54	55,04
Толщина стенки, мм	1,03–1,6	1,22–1,825	1,46–2,09
3D-модель	®W?{I ЖшШ М11Ш1 i^^sf ill	Цо ^ я^	®iiB

в

а

б

г

Рисунок 8. Испытательная оснастка: а – захваты на растяжение; б – пуансоны на сжатие; в – метки для измерения деформаций; г – тензорезисторы

Испытания на растяжение и сжатие проводились со скоростью движения траверсы 1 мм/мин. В ходе испытаний фиксировались диаграммы «нагрузка – перемещение», «напряжение – продольная деформация», а также «поперечная – продольная деформация» для образцов на растяжение. Всего было испытано 3 образца на растяжение и 2 образца на сжатие различной длины. Диаграммы деформирования, полученные в результате испытаний, представлены на рисунках 9 и 10.

Как видно из рисунка 9, диаграмма деформирования образца 1 существенно отличается от остальных образцов и имеет продолжительную стадию текучести. Данный эффект может объясняться неполной полимеризацией материала образца под действием ультрафиолета при 3D-печати. Таким образом, технологические параметры изготовления стандартных образцов и образцов ячеистых структур требуют тщательного контроля, чтобы обеспечить минимальный статистический разброс механических свойств материала.

Диаграммы деформирования при сжатии короткого и длинного образцов также отличаются. Короткий образец продемонстрировал эластичный характер деформирования, свойственный резинам. При достижении деформации более 25 % испытание было остановлено. Длинный образец в процессе испытаний потерял устойчивость при деформации 7,8 %, в связи с этим испытание также было остановлено.

По диаграммам деформирования были рассчитаны усредненные характеристики механических свойств исследованного материала, которые представлены в таблице 4.

4. Механические испытания образцов ячеистых структур

Как было сказано ранее, для механических испытаний были изготовлены образцы ячеистых структур на основе примитивов двух типов – Gyroid и I-WP (рисунок 11). Полученные образцы с ячеистой структурой имели квадратное сечение шириной 40 мм и высотой 60 мм. На торцах располагались плоские площадки толщиной 4 мм для равномерного распределения нагрузки. Таким

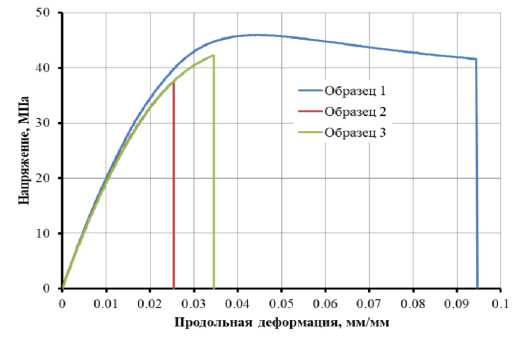
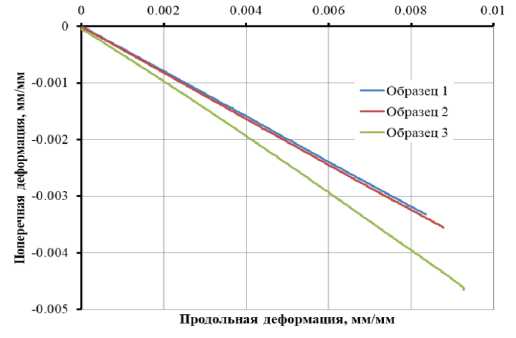
Рисунок 9. Диаграммы деформирования образцов на растяжение

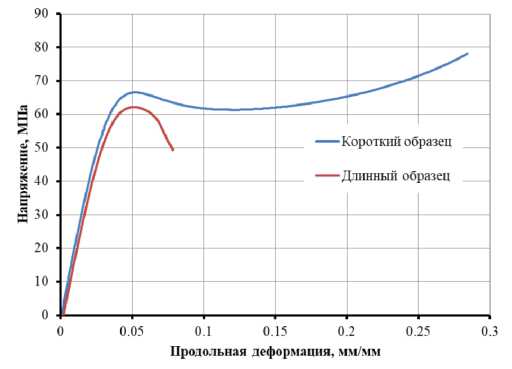
Рисунок 10. Диаграммы деформирования образцов на сжатие

If

ОСМИЧЕСКИЕ АППАРАТЫ И технологии aesas

Том 8

Характеристики механических свойств материала Anycubic ABS-Like Resin Pro 2

Таблица 4

Характеристика	Значение
Модуль упругости при растяжении, МПа	1943
Предел прочности при растяжении, МПа	41,97
Коэффициент Пуассона при растяжении	0,433
Модуль упругости при сжатии, МПа	2068
Предел прочности при сжатии, МПа	64,33

Рисунок 11. Образцы ячеистых структур

образом, суммарная высота образцов составляла 68 мм. Для каждого типа структуры, согласно таблицам 2 и 3, варьировался параметр t , определяющий толщину стенки примитива.

Образцы испытывались на сжатие на универсальной испытательной машине Tinius Olsen 100ST при помощи плоских пуансонов (рисунок 12а). Скорость нагружения составляла 3 мм/мин. В ходе испытаний фиксировались нагрузка и перемещение траверсы, а также посредством видеоэкстензометра перемещения четырех точек, расположенных вертикально в ячейках по центру образца (рисунок 12б).

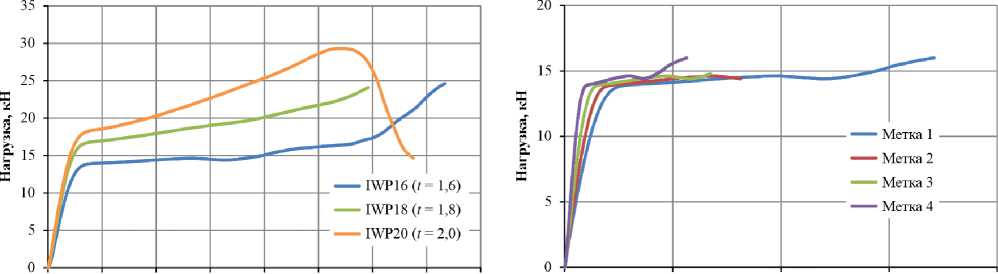
Полученные диаграммы нагружения образцов ячеистых структур I-WP имеют два выраженных участка с различным характером возрастания нагрузки (рисунок 13а). Первый участок в диапазоне перемещений от 0 до 2,5 мм близок к линейному, характеризуется большей жесткостью и соответствует упругому деформированию образца. На втором участке с меньшей жесткостью значительнее проявляются эффекты пластического деформирования материала. При дальнейшем увеличении нагрузки на характер деформирования начинают влиять эффекты контактного взаимодействия ячеек структуры и локального разрушения. Это, соответственно, проявляется в виде областей роста и падения нагрузки. Также из диаграмм следует,

аб

Рисунок 12. Испытания ячеистой структуры: а – испытательная машина; б – образец с метками что с увеличением параметра t жесткость образцов увеличивается на всех стадиях деформирования. Диаграммы перемещения меток на образцах I-WP аналогично имеют две выраженные стадии. На рисунке 13б представлены диаграммы для образца IWP16. Аналогичный характер перемещения меток наблюдался на образцах IWP18 и IWP20.

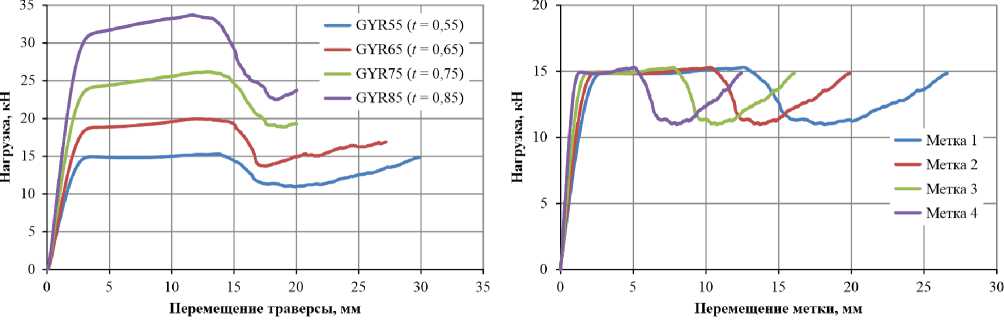
Диаграммы нагружения и перемещения меток для образцов ячеистых структур типа Gyroid имеют схожий характер по сравнению со структурой типа I-WP (рисунок 14). Увеличение параметра t, определяющего толщину стенки примитива, ведет к увеличению жесткости образца. Снижение нагрузки и ее незначительный подъем на конечной стадии деформирования соответствуют началу разрушения и сдавливанию ячеек. Данные эффекты можно визуально проследить на кадрах видеосъемки, представленных на рисунке 15.

О 5 KJ 15      20      25      30      35      '10            0                5                10               15               20

Перемещение траверсы, мм                                          Перемещение метки, мм

аб

Рисунок 13. Диаграммы нагружения образцов ячеистых структур I-WP: а – при различных значениях t ; б – перемещения меток образца IWP16

а

б

Рисунок 14. Диаграммы нагружения образцов ячеистых структур Gyroid: а – при различных значениях t ; б – перемещения меток образца GYR 55

Рисунок 15. Характерные этапы деформирования образцов ячеистых структур

ОСМИЧЕСКИЕ АППАРАТЫ И

ТЕХНОЛОГИИ вин

Заключение

С учетом изученного опыта предыдущих исследований авторами были смоделированы и изготовлены ячеистые структуры на основе TPMS типа Gyroid и I-WP. Для этого применялось открытое программное обеспечение MSLattice и технология фотополимерной 3D-печати. Изготовленные образцы позволили провести апробацию широко применяемого экспериментального подхода по изучению жесткости и прочности ячеистых структур. Полученные в результате механических ис- ¹⁸⁰ пытаний данные свидетельствуют о нелинейном характере деформирования образцов ячеистых структур. Данная нелинейность обусловлена

Том 8

пластичностью материала, разрушением ячеек и их контактным взаимодействием при сжатии. Относительная плотность ячеистой структуры, определяемая параметром t , прямо влияет на жесткость образца. Характер данного влияния целесообразно изучить в сравнении с численным моделированием, которое является перспективным продолжением данных исследований.

Работа выполнена в рамках государственного задания Минобрнауки России для Федерального исследовательского центра информационных и вычислительных технологий.