Проектирование клотоидной трассы путем аппроксимации последовательности точек с применением методов нелинейного программирования

Суть метода проектирования трассы путем аппроксимации последовательности точек заключается в том, чтобы путем соответствующей обработки на компьютере математической модели эскизной линии (рисунок 1) определить положение и все геометрические характеристики клотоидной трассы, отвечающей требованиям, предъявляемым к ней. При этом трасса должна наилучшим образом аппроксимировать заданную эскизную линию, т. е. геометрически неправильную приближенную трассу. Эскизная линия может получаться автоматически, например, с использованием метода проектирования оптимальной «цепочечной» трассы или может быть намечена проектировщиком по материалам аэрофотосъемки или топографическим планам, исходя из экономических и других соображений, и с помощью автоматических регистраторов координат введена в память ЭВМ.

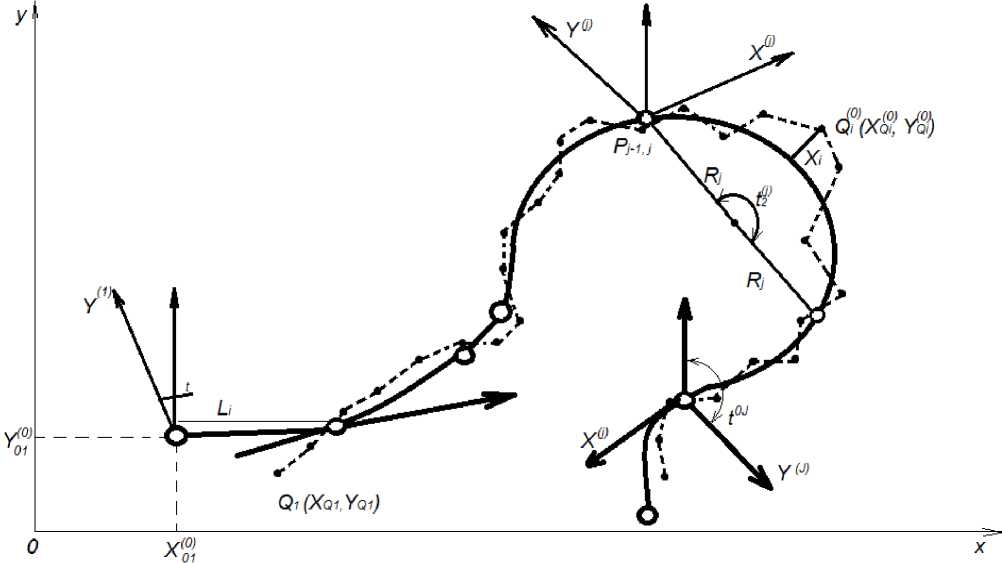
Рисунок 1. Расчетная схема метода аппроксимации последовательности точек: пунктирная линия – эскизная линия, сплошная линия – клотоидная трасса

Figure 1. Calculation scheme of the method of approximation of a sequence of points: a dashed line – a sketch line, a solid line – a clothoid trace

Проектируемая трасса состоит из отдельных элементов: клотоид, отрезков клотоид, круговых и прямых, соответствующим образом соединенных между собой. В целях удобства сопоставления метода аппроксимации последовательности точек с методом сглаживания эскизной линии трассы, предложенным в работе [1], принятые условные обозначения, по возможности, унифицированы: j – индекс, указывающий номер элемента трассы (j = 1, 2…, J); i – индекс, указывающий номер точки (i = 1, 2..., I); X(0),Y(0) - координаты в общей системе XOY; X(1), Y(1) - координаты!, в i-той частной системе; р^(X(0, Y'0)), P2°°( X20), Y20) - соот- ветственно начальная и конечная точки i-го эле- мента в общей системе координат; T0, Ti)

–

угол, наклона касательной в начальной и конечной точке i-го элемента относительно общей системы координат; Qi0^xQ0), yQ0)) - точка i-го элемента в общей системе координат; TQ) - угол наклона касательной в точке Q^ относительно общей системы координат; Pi(°' (V"+1, Yi() - точка стыка j-го и (j + 1) – го элементов в общей системе координат; т01 - угол поворота j-ой системы относительно общей системы координат; Aj, R1j, R2j, Lj – параметр клотоиды, радиус в начале и конце элемента, длина j-го элемента; zi – отклонение трассы от i-той точки; Vxi , Vyi – соответствующие проекции Zi на оси X(0) и Y(0); V – вектор проекций отклонений V=[V, 1, Vy 1 -, V1, Vyi].

Индекс N используется для приближенных значений величин.

Для геометрических характеристик распространяется правило знаков. В методе аппроксимация последовательности точек принято отличное от метода опорных элементов правило назначения частных систем координат для каждого элемента трассы, что обусловлено специфическими особенностями метода. Начало каждой i -ой частной системы координат совпадает с начальной точкой j -го элемента, а ось X ^{( j )} совпадает с касательной в начальной точке j -го элемента и направлена по ходу расчета (рисуно к 2)

Рисунок 2. К выводу линеаризованных уравнений отклонений оси

Figure 2. The derivation of the linearized equations of the deviations of the axis

В отличие от метода опорных элементов метод аппроксимации последовательности точек предусматривает задание избыточного количества точек. В общем случае, через все заданные точки не может быть проведена удовлетворительная трасса, поэтому задаваемые точки эскизной линии рассматриваются лишь как «приближение» точки, около которых должна пройти ось пройти ось проектируемой дороги, а задача относится к классу условно-экстремальных.

На основе проведенного анализа выявлена целесообразность решения поставленной задачи с использованием методов математического программирования. Для этого необходимо:

─ систематизировать требования к геометрии трассы и представить их в виде соответствующих ограничивающих условий;

─ исследовать целевую функцию и выбрать класс возможных методов для решения данной задачи;

─ разработать методику проектирования трассы.

Основная часть

В качестве основных переменных при проектировании трассы по методу аппроксимации последовательности точек с учетом анализа работы [2] приняты: N X 00 ) , А У ^⁰ ) - приращение координат начала трассы; Ат ⁰¹ - приращение угла поворота частной системы первого элемента относительно общей системы; А т - изменение центрального угла круговых кривых (l элементов); NL - изменение длины прямых ( m элементов); NR - изменение радиуса круговых кривых ( n элементов); АА - изменение параметра клотоид (p элементов).

Одно из основных требований, предъявляемых к проектируемой трассе лесной автомобильной дороге, необходимость обеспечения ее непрерывности и плавности. Они соблюдаются в пределах элементов трассы: клотоид, круговых кривых и прямых. Дополнительно необходимо, чтобы в точках стыка элементов координаты X j и У ⁰

и направление касательной т ( j ) в начале последующего ( i -го) элемента точно соответствовали координатам X 20 j _-1 ) и У ^) и направлению касательной т 20 ) 1 ) в конце предыдущего ( i -1) элемента:

1 i            2 ( i -1 )

у ( ⁰ ) - у( ⁰ )

• ^y1i    = ^У 2 ( i -1 )

• -( 0 ) _ -( 0 ) ‘ 1 i = ‘ 2 ( i -1 )

  
  

  При радиусах закруглений меньше определенной величины (обычно 2000 м) трасса должна также удовлетворять требованиям второго порядка плавности, то есть в главных точках смежные элементы должны иметь одинаковые радиусы закругления, направленные в одну сторону:

^R1i = R 2 ( , -1 )                        (²)

Требования (1) и (2) учтены при формализации функции цели. В случае использования существующих мостов или других сооружений, на примыканиях к уже построенным или ранее запроектированным участкам дороги, а также при корректировке промежуточных участков проектируемой трассы может возникнуть необходимость обеспечить прохождение расчетной трассы через заранее определенные фиксированные точки, в заданном направлении и с заранее установленным радиусом кривизны в данной точке.

В работе [3] для этой цели предлагается ввести ограничения величин V i и t Q ° :

t U< V i <  1 2i                   (3)

где t 1i , t 2i – соответственно нижняя и верхняя границы проекции отклонения i -ой точки;

• ^T 1 <  ^TQ <  ^T 2                 ⁽⁴⁾

где т 1 , т ₂ - соответственно нижняя и верхняя границы t Q ° . Точке примыкания задается как одна из точек эскизной линии трассы.

Для случая, когда точка Q находится на k -том элементе, имеем:

• Т? = Т . V ( т 2 j ^{-1 )} - Т ( > ) ₊ т - ) )     (5)

.j = 2

Если в качестве неизвестных приняты А т ⁰¹, Ат 2 j ) , А т 1 ⁽‘) , Ат ^ , то (5) можно представить в виде:

_т ⁽⁰⁾ ₌ ⁰ i ₊ ⁽⁰⁾₊ у ( д ⁽ j ^-1)д ⁽-) ) ₊ д ^{( -} )

• ^T Q ^T ' ^T QN ⁺ ^ ( ^{А Т} 2 ^{А Т} 1 )^^Al Q

• .    j = 2

Для определения А т 2 j ) , А т 1 ⁽‘) , А т ^^- ) в [4] приведены формулы в зависимости от сочетания смежных элементов и от типа k -го элемента.

Вследствие значительных сложностей, связанных с учетом ограничений вида (3) и (4), в одном из вариантов программ, реализующих метод аппроксимации последовательности точек, принято решение обеспечивать условия примыкания в конце проектируемого участка трассы путем введения на участке примыкания 3-x точек с большими весами Р i . Это обеспечивает близкое, но не строгое, решение в узле примыкания. Окончательная увязка может быть выполнена по методу опорных элементов.

Часто бывает необходимо ограничить зону варьирования трассы, что может быть вызвано целесообразностью обхода различных препятствий или зон, где проложение дороги связано с существенным удорожанием строительства (оползней, осыпей, затопляемых участков и т. п.). Эти требования могут быть удовлетворены путем введения ограничений, устанавливающих допуски отклонения расчетной трассы от точек эскизной линии в поперечном направлении к трассе. Данные ограничения могут быть представлены в виде неравенства:

Z . <  Z <  Z               (7)

min ii   max i

Такая форма представления ограничений удобна тем, что позволяет задавать как симметричные, так и несимметричные зоны варьирования.

Из условия обеспечения безопасности и удобства движения на закруглениях абсолютные величины радиусов кривых в плане |R i | не должна быть менее минимально допустимых R min , установленных в зависимости от расчетной скорости по СНиП 5-72 или соответствующими расчетами:

R min <  R i |,( R min >  0)            (8)

Так как поиск осуществляется в пределах обусловленной начальным приближением последовательности элементов трассы, то знак радиуса при оптимизации не меняется, следовательно, разобщенности допустимой области не будет и ограничения в соответствии с работой [5] можно представить в виде:

• -    sign ( R i ) xA R j <  - R _m„ + | R.|        (9)

Аналогичный характер имеют ограничения величины параметров клотоид:

A min <  R i |, ( A min >  0 )             ₍₁₀₎

• ^-    Sign ( 4 ) ^{ХА А} j <  ^{- A} min ⁺ | ^Ai|

где A min – минимально допустимый параметр клотоиды.

В ряде случаев возникает необходимость ограничивать длину элемента, что обеспечивается двусторонним неравенством вида:

L . <  L <  L              (11)

min ii max i где Lmin i; Lmax i – нижняя и верхняя границы Li.

Ограничения для прямолинейных элементов трассы с переменной длиной приобретают вид:

L - L <А Ь <  L - L (12) min i         i max i

Для круговой кривой с переменным центральным углом используются ограничения вида:

• т ⁽ i ). —t⁽ii ) T)i ) —t⁽ i )         (13)

2 min 2         2      2 max 2

где T 2 im_in , t 2 max - нижняя и верхняя границы т 2 i ) .

В [5] на основании исследований и опыта эксплуатации дорог, запроектированных по принципам клотоидного трассирования, предложен ряд рекомендаций для назначения геометрических характеристик элементов трассы. Так, например, в целях улучшения зрительной плавности дороги рекомендуется, чтобы величины параметров А переходных кривых находились в пределах от 0,4 R до 1,4 R . В общем виде для случая, когда i -ый элементов – круговая кривая, а ( i + 1) – клотоида:

А .

d 1 i <     <  d 2i               (14)

Ri

A где d 1i; d2i - нижняя и верхняя границы —i+1.

R i

Соотношение параметров смежных клотоид на обратных закруглениях должно быть в пределах:

Или в общем виде:

A d3^ A < d4i          (15)

A i + 1

A где d 3i ; d 4i – нижняя и верхняя границы ⁱ .

A + 1

Используя первые два члена разложения в ряд Тейлора для функций двух переменных как это предложено в работе [5] и, принимая во внимание, что для смежных круговой кривой и клотоиды sign R i = sign A i+1 , имеем:

4- xA Rj - A xA A, + 1 < d 2 i-A (16)

A+1      j A2+1

• — — xA R, - A xAA, ₊,< - d_u - -R - (17)

A          j A2                   1 iA

A+1           Ai+1

Аналогичны для (15), принимая во внимание, что sign A ^ sIgA _{+ 1} имеем:

1 A A

• — : xAAj ' . x AA-+1

Ai+1     j amA

1 A A

----x A A x A A, ₊j <  - d₃,— (19)

A          j A2         +13

Ai+1            Ai+1

Рекомендуется [4], чтобы радиусы круговых кривых, сопрягаемых S -образными клотоидами, отличались друг от друга по абсолютной величине не более чем в 3 раза, или в общем виде:

d_5[ <     <  d_6[              (20)

5 i 6 i

R i + 1

Используя разложение в ряд Тейлора, получаем:

• —    xA R, +     xA R ₃< d ₆,+ A (21)

• j2          i–36

Ri–3           Ri–3

• — xAR, - A xAR, 3< - d. - R^- (22) j2            i–33

Ri–3           Ri–3

С учетом вышеотмеченного, требования к геометрическим характеристикам и положению трассы могут быть учтены с помощью системы линейных неравенств вида:

^b 11 ^ 1 ^{+ b} 12 x 2 +-+ ^b 1 m x m <  ^d 1

b 21 ^x 1 ⁺ b 22 x 2 +_+ b 2 m x m <  d 2

^                 (23)

b„X + b„iX^ + — + b„„,x„, < d„ n11 n2 2         nm m n где m – число переменных; n – число ограничений.

В матричной форме эта система принимает вид:

BX <  D             (24)

Предусмотрено несколько способов получения информации об эскизной линии трассы, объем которой довольно велик (до 2000 шестизначных чисел). Хотя обычно для получения ее используются автоматические регистраторы данных, возможность ошибок не исключена [6 ,7]. Поэтому в системе реализован программный контроль информации, позволяющий обнаружить грубые ошибки путем анализа углов ^ _t между смежными отрезками эскизной линии.

В автоматическом режиме ошибочные точки исключаются из массива в оперативной памяти и из файлов. При работе в диалоговом режиме с кодом 2 предусмотрена возможность просмотра и корректировки данных об эскизной линии трассы и всей информации, связанной с ней.

Параметром диалоговой функции является номер точки эскизной линии, с которой начинается очередная «страница» (формат экрана). Одновременно на экране размещается информация о десяти точках. В стандартном режиме просмотр осуществляется последовательности от начала до конца сегмента, при этом параметр формируется программно и проектировщик только меняет «страницы» нажатием клавиш «ВВ». При выборочном просмотре или необходимости возврата назад следует на экране указать номер точки, с которой должна начинаться очередная «страница» (формат экрана).

Предусмотрены различные корректировочные средства:

• а)    замена содержимого массивов;

• б)    добавление точек;

• в)    удаление точек и др.

Возможны различные способы формирования исходного приближения для проектирования трассы по методу аппроксимации последовательности точек.

Используя диалоговую функцию с кодом 3, можно осуществлять просмотр и корректировку исходного приближения.

На экране можно выполнить корректировки вида:

• а)    замена геометрических характеристик элементов трассы;

• б)    удаление и добавление элементов.

В процессе работы блока оптимизации выполняется аппроксимация эскизной линии элементами трассы в пределах первоначально заданной последовательности, то есть меняются только величины геометрических характеристик элементов, но не их количество и тип. Вместе с тем независимо от способа формирования исходного приближения, довольно часто появляется необходимость просматривать варианты проектируемой трассы, отличающиеся последовательностью элементов.