Проектирование конвертеров с широтно-импульсной модуляцией на основе метода гармонической линеаризации

Одним из основных элементов электропреобразова-тельной аппаратуры (ЭПА) системы электропитания (СЭП) спутника является преобразователь постоянного напряжения в постоянное - конвертер, основная задача которого состоит в стабилизации напряжения на выходе СЭП. Процесс проектирования ЭПА в составе СЭП осложняется тем, что конвертор любой топологии (с параллельным или с последовательным включением ключевого элемента) представляет собой систему автоматического регулирования с широтно-импульсной модуляцией (ШИМ), которая относятся к классу нелинейных импульсных систем.

Синтез конвертеров с ШИМ на начальной стадии проектирования сводится к расчету периодических процессов в нелинейной системе. Для решения этой задачи используются методы теории нелинейных колебаний, которые могут быть условно разделены на графоаналитические, численные и аналитические.

Среди графоаналитических методов следует отметить метод фазовой плоскости для качественного исследования нелинейных колебаний.

Численные методы решения являются основными методами анализа в современной практике научно-инженерных расчетов. Это группы широко распространенных явных и неявных методов решения систем обыкновенных дифференциальных уравнений, однако при их алгоритмической и программной реализации в расчетах периодических процессов в конвертерах могут возникать недетерменированные выходные сигналы, например стохастические режимы или «биения» в вычислительном эксперименте, что создает значительные трудности для разработчиков ЭПА. Принятие проектного решения в данном случае будет полностью зависеть от опыта и квалификации разработчика. Кроме того, применение математического описания конвертеров в виде системы дифференциальных уравнений позволяет решать задачи параметрического синтеза, но существенно затрудняет решение задач структурного синтеза.

Указанных проблем лишены аналитические методы расчета периодических процессов в нелинейных системах, например методы асимптотических разложений, гармонического баланса и гармонической линеаризации. При этом, несмотря на большой объем и сложность аналитических преобразований, одним из главных их достоинств является возможность выполнения анализа периодических процессов при символьном задании параметров ЭПА и обозрения процессов в целом, что может значительно повысить эффективность принятия проектного решения на этапе функционального проектирования.

Рассмотрим применение метода гармонической линеаризации при проектировании конвертера понижающего типа с ШИМ (рис. 1,2).

Рис. 1. Схема конвертера

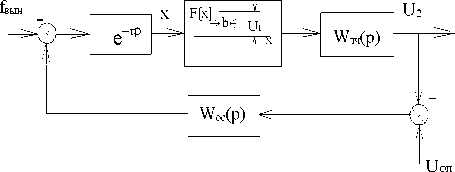
Рис. 2. Структурная схема конвертера е^ч - звено запаздывания, моделирующее запаздывание срабатывания транзисторного ключа; А[х] - релейный элемент, моделирующий работу ключа; И⁷_лч(р) - передаточная функция участка схемы вход-выход фильтра^^ - источник вынужденных колебаний, моделирующий работу генератора пилообразного напряжения; И⁷ (р) - передаточная функция, вид и параметры которой необходимо определить

Как это следует из принципа работы конвертера, в нем всегда присутствуют вынужденные периодические колебания. Однако эти колебания при определенных параметрах элементов конвертера порождают автоколебания, которые могут существенно повысить коэффициент пульсаций выходного напряжения или привести к потере устойчивости.

Задача синтеза в этом случае сводится к определению передаточной функции W (р), которая позволила бы исключить возможность возникновения автоколебаний.

В соответствии со структурной схемой (рис. 2) уравнение динамики системы имеет вид [1]

х+^л»е-‘р^ос(р)А[х] =

= W (р) U -f (?).               (1)

О.С^ z о.п ^вын4 z                        х z

В уравнении (1) принято допущение /вын(0 = = Bsin(co2 Э).

Периодический процесс может быть представлен в виде

\ = \„+\.. (2) гдеХ_м= Х_о+Х_А - медленно меняющаяся составляющая, здесь Х_о - постояннаясоставляющая; Х_а = Д -бтС) -t) -переменная составляющая, характеризующая автоколебания; a>j - частота автоколебаний; Х_г = 4 -sin(a)₂ -/+<р) -переменная составляющая, характеризующая вынуяеденные колебания в системе, здесь со₂ = Тп.]Т - частота вынужденных колебаний (Г- период переключения).

Амплитуда вынуяеденных колебаний определяется по выражению

___________________________ЛЗ)

0(/со₂) + Л(/со₂) • е^^тг ■ W_oc (/со₂) • (? + ;V)|²

где W^^ = R(p)/Q(p)\ q,q’ - коэффициенты гармонической линеаризации:

11'          м । I1'М

V А? V 4²

\ 1               2             1               2/

?U) = "

2-4 •/>

4 - л

Характеристика нелинейного звена

FM = F°C424m)+№W + где F°(A,X ) = — +    1 arcsin+ ^м -arcsin-——1.

м 2            44 J

Решая (4), для заданной нелинейности F[x] можно определить функцию смещения:

F4A2,X^QC),(5)

которая в дальнейшем используется при определении автоколебательного режима и решения уравнения для постоянных составляющих. Для этого линеаризуем функцию смещения Ф(А') в пределах рабочего режима системы:

Ф(Х ) = Ф° + К -X , v м -'                  а а ’

АФ где Х_а = -—

С учетом (4), (5) и (6) система уравнений для определения возможности возникновения автоколебательного режима имеет вид

6(0)4+40) 4,.с(0)Ф°=

= ^.с(°)^пе(0),

Q(p)Х_А + R(p) е"' W_{o c}(p) кх_а = 0.        (7)

После подстановки в (7) p=jto_x определяются А). .1 и со т. е. условия возникновения или отсутствия автоколебаний в системе, на основании чего делается заключение об устойчивости системы. Изменяя W (р) и используя изложенную выше методику, можно синтезировать рассматриваемый конвертер исходя из обеспечения отсутствия автоколебаний в системе.

Представленный метод был использован при анализе и синтезе конкретного конвертера.

Передаточная функция линейной части этого конвертера имеет вид

W (р) =-----------, л ч а2 • р1 + ах • р +1

где К_лч = 4/(4^+ri) -коэффициентпередачи,здесь4 - сопротивление нагрузки, г_х - активное сопротивление обмотки дросселя фильтра; а₂ = К -L-С, здесь L - индуктивность дросселя фильтра; С - емкость конденсатора фильтра; а_х = (L+R_H-r_x-C)/(R_H+r_x).

Расчеты проводились при следующих исходных данных: частота преобразования 25 кГц; U_x = 40 В; U_on = 27 В; L = 10 мкГн; С= 5 мФ; г = 0,01 Ом; 1= 1 мкс; 4⁼ 1 ®^Mi В = 0.2 В: /А-передаточная функция звена обратной связи, К = 1; b - зона нечувствительности компаратора, Ь = 0,001.

Согласно [2] и рис. 2, процессы в конвертере с ШИМ описываются уравнением динамики (1). Решение этого уравнения находится в виде (2) из системы уравнений для медленно меняющихся и колебательных составляющих. После решения (4) определяется функция смещения (5), линеаризуемая в пределах рабочего режима конвертора (6). Рассчитанные функции смещения при различных значениях параметров фильтра (рис. 3) показывает, что значение 4 в рабочей точке равно 14... 15.

Уравнение (1) теперь примет вид (7), и неизвестные A_v cOj иХ_о определяются из (7) подстановкой р =Ja_x:

1-а₂ -т² + К. -К^ - К -cos^j -т) = 0, а_х -со. -К -К -X-si^co.-т) = 0,         (8)

х0 + клч-к-ф° = к

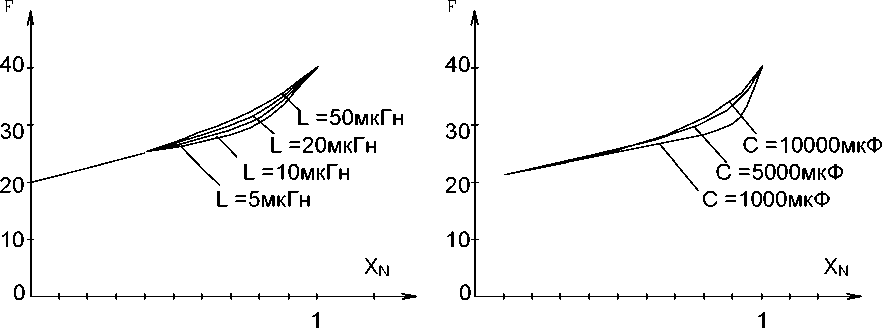
Рис. 3. Функции смещения

При решении (8) частота предполагаемых периодических колебаний/^ намного меньше частоты вынужденных колебаний. Отсюда величина 271/"-т = ю -т мала и sin (сут) » cOj-t, a cos (сут)« 1. Искомое решение для автоколебаний системы, те. условие их существования, определится по выражению гг-С + LYH-К-т-Ка =0 . (9)

При подстановке значений параметров в (9) следует, что в системе отсутствуют автоколебания. Однако если совместное запаздывание ключа и компаратора будет равно 4 мкс, то в системе возникнут автоколебания с частотой 2,5 кГц.

Рассмотренный выше конвертер является основой системы электропитания космических аппаратов, качество работы которой обусловлено протекающими в ней электромагнитными процессами. Представленная методика анализа и синтеза конвертеров СЭП как нелинейной системы позволяет на схемотехническом уровне проектирования на основании заданных критериев исследовать и формировать электромагнитные процессы как в конвертере, так и во всей СЭП в целом.

Предложенная в статье методика структурно-параметрического синтеза конвертеров с широтно-импульсной модуляцией позволяет, используя хорошо апробированный метод, с высокой точностью решать задачи анализа и синтеза: оценивать устойчивость системы и синтезировать ее, исходя из заданных запасов устойчивости. Рассмотренный метод хотя и позволяет уже сейчас решать большое количество задач, связанных с синтезом конвертеров, однако требует дальнейшего развития для решения более сложных проблем, например анализа и синтеза конвертеров, работающих в режиме прерывистых токов дросселя.