Проектирование математической модели системы автоматического управления магнитной левитации

Известно, что на электрический заряд, перемещающийся с какой-либо скоростью в электромагнитном поле, воздействует магнитная сила (МС) [1]. Вблизи намагниченных тел (магнитов) или проводников с током МС в одних условиях является силой притяжения, а в других - силой отталкивания. Это свойство служит предпосылкой для создания систем, управляющих левитацией электропроводящих предметов.

В настоящее время эффект электродинамической магнитной левитации (ЭМЛ) используют в различных технических устройствах [2, 3]. Наибольший объем исследований в области ЭМЛ связан с перевозкой разнообразных товаров с целью создания высокоэффективного «парящего» транспорта [4].

Сам эффект ЭМЛ появляется, когда рядом с проводящим элементом (проводником) находится или постоянный магнит в состоянии вращения или поступательного перемещения; или катушка с током. В данной ситуации начинает происходить процесс генерации переменного магнитного поля в области проводящего элемента, которое, в свою очередь, запускает процесс генерации (наводки) вихревых токов в самом проводнике, которые также генерируют магнитное поле, но в противоположном направлении. При этом возникает отталкивающая сила между проводником и источником магнитного поля. Данный процесс служит базовым принципом при взаимодействии любых левитирующих тел (ЛТ).

На эффекте ЭМЛ базируется функционирование магнитных и электрических подвесов. На сегодняшний день широко используются следующие основные типы: на постоянных магнитах, активные магнитные, LC - резонансные, диамагнитные, сверхпроводящие, магнитогидродинамические, индукционные.

Основной проблемой ЭМЛ является динамическая устойчивость ЛТ. Объяснение этому дает теорема Ирншоу, утвер- ждающая, что “Всякая равновесная конфигурация точечных зарядов неустойчива, если на них кроме кулоновских сил притяжения и отталкивания не действуют иные силы” [5]. Для магнитостатики в случае фиксированных токов данная теорема также справедлива. Другими словами, данная теорема утверждает, что нельзя получить устойчивую ЭМЛ, используя статические электромагнитные поля. Отсюда следует, что для получения эффекта ЭМЛ, необходимо при помощи переменного электромагнитного поля создать потенциальную яму в области, где происходит ЭМЛ. Этого можно достигнуть, например, за счет индукционной катушки, генерирующей переменное электромагнитное поле. Для того, чтобы ЛТ оставалось в заданной области, необходимо соответствующее управление этим полем.

Отсюда следует актуальность работ, связанных с необходимостью разработки таких систем автоматического управления (САУ), которые могут подавлять возникающее колебательное движение ЛТ. Большинство существующих САУ ЭМЛ вырабатывают управляющие воздействия, которые приводят к недостаточному подавлению колебаний ЛТ. Вследствие этого вибрации могут вывести ЛТ из требуемой области равновесия. Устранение перемещения ЛТ из зоны равновесия и/или возвращения в нее можно осуществлять разными методами, например, при помощи катушки с током (электромагнита).

Широко распространенные современные САУ в основном базируются на ПИД – регуляторах. Основные недостатки в таких САУ проявляются в канале производной сигнала ошибки, связанное с тем, что усиление канала влечет прямопропорциональное возрастание частоты. А это в свою очередь:

– уменьшает отношение полезной составляющей управляющего сигнала к шу- мовой, вызывая дестабилизацию объекта управления;

– во время сверхдинамичного процесса смены уровней ошибки, даже если первая производная сигнала от времени небольшая, САУ может подать импульс большой амплитуды на вход дифференциатора.

Кроме того, необходимо отметить, что интегральное насыщение служит причиной ухудшения качества переходного процесса. В этом случае его характеристики в значительной степени отличаются от расчётных характеристик по линейной модели регулятора.

Но тем не менее, несмотря на вышесказанное, в случаях, когда ПИД – регуляторы обеспечивают требуемое управление, их достаточно часто применяют. Это относится и к данной задаче.

В общей постановке описание поведения ЛТ в переменном электромагнитном поле происходит при помощи математического аппарата теории нелинейных и неустойчивых систем. А это в свою очередь делает задачи моделирование поведения и управления ЭМЛ достаточно сложными.

В работе рассмотрен относительно быстрый процесс с периодом порядка миллисекунд. Таким процессом достаточно трудно управлять.

Разработка математической модели динамики ЛТ

Движение проводящего ЛТ в магнитном поле опишем при помощи второго закона Ньютона. В этом случае считаем, что на ЛТ с массой m действуют три силы: вес тела (сила тяжести) P = mg , электромаг-F нитное взаимодействие m с полем ка-

F тушки, и демпфирующая сила ^D , действующая в противоположном направлении с вертикальной скоростью ЛТ в любой момент времени. Схематически это представлено на Рис.1.

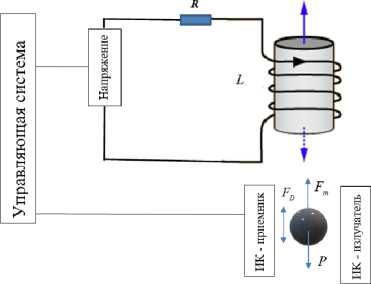
Рис. 1. Схематическая схема представления эффекта левитации в магнитном поле катушки с током

Рис. 1 можно сопоставить следующему физическому процессу. До некоторого момента времени t 0 электрический ток i ⁽ t ⁰ )

i ( 1_й ) = 0

на катушку не подается (  0    ) и ЛТ лежит на подложке. В момент времени t0

на катушку подается соответствующее напряжение, ЛТ отрывается от подложки, поднимается до заданной точки и начинает левитировать, то есть создается эффект «парения» ЛТ. Необходимо отметить, что подъем и опускание ЛТ происходят с достаточно большой частотой в ограниченном диапазоне высот. Контроль высоты может происходить разными способами. Например, при помощи датчика Холла или, как показано на Рис. 1, инфракрасного датчика.

Уравнение движения, согласно второму закону Ньютона, можно записать следующим образом:

dv (t)

-P + F -F

¹ + m D D

m dt

v (t )=dzid где       dt – вертикальная скорость (изменение высоты) ЛТ;

z (t)

– вертикальное расстояние от центра ЛТ до подложки;

FD = kDv ( t ).

;

k

^D – коэффициент демпфирования;

^m – масса ЛТ;

^t – время.

F

Сила m , из-за наличия железа в сердечнике катушке, фактическая является сложной нелинейной функцией, зависящей от многих параметров, например, от геометрии, индуктивности, количества желе- за, присущему железу гистерезису и т.д. [6]. Но для решения поставленной задачи достаточно взять лишь линейную часть этой функции. Аппроксимация первого порядка дает следующее выражение:

-2< t L) H ^{- z (} t )J

где H – расстояние от катушки до подложки;

^{k m} – постоянный коэффициент, зависящий от параметров катушки, определяемый экспериментально.

Таким образом сила ^m пропорциональна квадрату тока, протекающего в катушке, и обратно пропорциональна квадрату расстояния между ЛТ и катушкой.

Исходя из Рис. 1, и согласно закону Кирхгофа для напряжения, можно записать уравнение для напряжения на катушке:

U (t ) = i (t) R + L

di (t)

dt

где ^R и ^L – сопротивление и индуктивность катушки.

Из этого уравнения следует:

di (t)

dt

-Ti(t) + TU(t)

Отсюда, учитывая (1)-(3), получаем следующую систему:

di ( t ) dt

- ^ i ⁽ t ⁾⁺2 U ⁽ t )

dv ⁽ t )_ kX ^f i ⁽ t ) Y

---- = — g +-----TV dt         m ^ H — z (t ),

—

k D _v

m

( t )

В дальнейшем, для удобства расчетов перейдем к новой переменной: ^z i ( t ) = ^{H - z} ( t )

Тогда:

dz_x ( t )      dz ( t ) d ² z_v ( t )      d ² z ( t ) dv ( t )

---- —-------- —---- —-- dt         dt      dt2         dt2

,, и (4) преобразуется к следующему виду:

di (t)      R , x 1,

-Al —--i ( t ) + - U ( t )

dt     LL

^dz- (t) dt dv-(t) dt

^{— v} 1 ⁽ t ^{) —— v (} t )

— g — k m m

¹ ( t ) I      k_D    < \

M -   v- (t)

Z i ( t ) J m

Таким образом, получили систему обыкновенных дифференциальных уравнений (5), которая является нелинейной моделью динамики проводящего ЛТ в магнитном поле катушки. Заметим, что в рассматриваемой постановке, будет измеряться, при помощи ИК-приемника и ИК-

датчика, только положение ЛТ в текущий

момент времени:

z- ( t )

Решение первого уравнения в (5) при

постоянном

U(A — U — c const const

дующий вид:

имеет сле-

i ⁽ t ) =

R

U     — t const^ + e L C

R ¹

C где 1 – константа.

Анализ уравнения (6) показывает, что со временем, при постоянном напряжении, ток достаточно быстро стремиться к уста-i (t)   ^„ > Uconst- новившемуся значению            R .

Подстановка этого значения в (5) приводит к ситуации отсутствия действительного решения (5). Это означает, что входное воздействие U ⁽ t ) не может быть постоян-

Разработка математической модели САУ ЛТ

Как известно, ММ САУ можно представлять через: пространство состояний, передаточную функцию и задания нулей и полюсов [7]. В данной работе выбрано пространство состояний (State space – SS). Формально представление непрерывной модели управления в пространстве состояний выражается следующим образом [0] :

ным.

' X = AX + Bu + Dw \y = CX

где X A

u

B

w D Y C

• -    вектор в пространстве состояний размером ^{n х 1};

• -    квадратная матрица размером ^{n х n} ;

• -    вектор управляющих воздействий размером m ^{х 1};

• -    матрица размером ^{n х m} ;

• -    вектор внешних возмущений размером p ^{х 1} ;

• ¹    - матрица размером ^{n х} p ;

• -    вектор измерений размером k ^{х 1};

• -    матрица размером k ^{х n}

.

В нашем случае вектор X представляет из себя следующее выражение:

X = ( X 1 , x 2 , Х 3 ) = ( i ( t ) , Z 1 ( t ) , V ( t ) )

.

Тогда

x

X = x₂

V ^x3 >

di (t) dt dzx (t) dt dv1 (t) dt

- Ri ( t ) + 1 U ( t )

V1(t)

g - k m m

z1(t)

- k D v ( t ) m

R

Lx ¹"

x g - km m

L

x 1

V x 2 у

k

D X g m

Здесь, для приведения (8) к общепринятому виду, введено обозначение u = U .

Необходимо отметить, что (8) лишь приближенно описывают динамику проводящего ЛТ в магнитном поле катушки. Это связано, как было сказано выше, со сложностью описания электромагнитного поля и наличием дополнительных не учитываемых воздействий с его стороны. Причем основные проблемы встают при описании динамики ЛТ в близлежащей области поверхности катушки.

В общем случае, для успешного решения задачи управления ЛТ, необходимо исследование ММ САУ на наблюдаемость и управляемость. В нашем случае это необходимо сделать в окрестности задан- z ной точки равновесия    равн ЛТ:

(x10,x20,x30 )=(i,^,zравн,0) . Обычно эту точку называют рабочей или номинальной. В этой точке должно выполняться требование:

- P + F — 0

m

.

то есть условие равновесия.

Отсюда следует:

mg = ^k m

x10

V x 20 J

mg

-^ X ^Q — ± --- x

m

x 20

или

.

Из физических соображений нужно брать mg

X10 — . ,  X 20 — x km

—

k m x10

mg

.

В случаях задания уставки, исследования на наблюдаемость и управляемость ММ САУ обычно проводят на линеаризованной в окрестности рабочей точки ММ.

Для нахождения матрицы Якоби, с целью линеаризации (8), введем следующие обозначения:

f , ^{( X} 1 , ^x 2 , ^x 3 , u ^{) — - R ( X} 1 ^{) + 1} u ; f ( x ,   ,  , u ) —   . ^{f 3 ( x}1 , ^x2 , x ³ , u ) g

LL 2 123  3

k

—— x ₃. m

Jacob (X 6H) —

равн

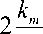
m

R

L 0

x 10

^{( x} 20 )

1
	0	0
	0	1
к 2 m m	2 x 10	- k D
	( x 20 )	m

Тогда матрица Якоби имеет следующий вид:

flf1 dxx df, dx2 f1 dx3 R L 0 1 0 ff1 au Jacob(X)— 5f2 5xi 5f2 dx2 5f2 axз — 0 0 2 1 k ; B — af2 au — dfl dfз dfl -2 m^  U V    m  (x 2 ) 2 ^m  U m  ( x 2 ) — 5f3 (axi dx2 dx3 J m J V au j f 11

L

V J

Следовательно, в рабочей точке матрица Якоби равна:

Если учесть (9), то матрица (10) примет следующий вид:

	г   R — L	0	) 0
Jacob ( X равн ) =	0	0	1
	—2 - g-	+2 - g-	kD —
	к     Х 10	x 20	m J

Отсюда следует, что линеаризованная (8) в окрестности рабочей точки имеет вид:

X =

x ₂

к ^x3 7

= AX + Bu =

R

—

L

x ₂

+

L 0

u .

Y = CX = ( 0  1  0 )

—2 g- x10

+2 -g- x20

k

—

m

= x 2

к ^x 3 7

Анализ разработанной математической модели САУ ЛТ

Для анализа на устойчивость разработанной ММ найдем корни следующего характеристического уравнения [0] :

R „ ---Я  0     0 L X = det | A — ЯЕ = det 0     —Я     1 ГR  ,) = — mx^ ol —+ Я 1 Я2 + kD Я — 2 -g- 1 к L   7 mx 2g   2g   kD -------Я 20 x10    x20     m (12) где E - единичная матрица.

Корнями этого уравнения являются следующие числа:

R . 1 ,  kD x 20 ^{+   8} m ^x 20 ^{g + k}D x 20

_L  2,3                _{2 mx}

Все корни характеристического уравнения (12) вещественные, причем один положительный. Отсюда следует, что система (11) является неустойчивой. Поэтому для сохранения устойчивости процесса ле- витации необходимо осуществлять соответствующее управление.

Для анализа на наблюдаемость (11), необходимо построить матрицу наблюдений и рассчитать ее ранг [0 ]:

				) 0
	Г C )	0	1
Obs C =	CA =	0	0	1
	к CA 2 J	2 g	2 g	— k D
		к   X 10	x 20	m J

Ранг этой матрицы равен трем. Следовательно (11) наблюдаема.

Для анализа на управляемость (11), необходимо построить матрицу управляемости и рассчитать ее ранг [0 ]:

	1      R        R 2
	L    L2       L
Control B = ( b AB  A 2 b) =	0   0     - 2g-
	x 10 L
	0   - 2 g   2 g R | 2 kD g
	(       X 10 L   X 10 L 2    mx i0L J

Ранг этой матрицы равен трем. Следовательно (11) управляема.

Таким образом, системой (11) в окрестности рабочей точки в принципе можно успешно управлять. Для этого необходима лишь соответствующая система управления. В данной работе, была применена система с ПИД-регулятором. Требование к контроллеру состоит в том, чтобы он мог позиционировать ЛТ в любом произвольном месте магнитного поля под катушкой и перемещать ЛТ из этого положения в рабочую точку. Эти требования фиксируются путем установления границ переходной характеристики для измерения местоположения ЛТ.

Результаты моделирования

Для моделирования динамических нелинейных систем в ходе данной работы был использован инструментарий, предоставляемый MATLAB [9-12 ].

На Рис. 2 представлена Simulink-модель процесса магнитной левитации. В ней использованы стандартные блоки и реализована система (11).

При проектировании нестабильных систем коэффициент усиления должен быть достаточно большим, чтобы сместить нестабильный полюс в левую полуплоскость. Поэтому изначально были взяты следующие коэффициенты ПИД-регулятора:

K p = 0.5; K_D = 0.0. K = 3.0;

График переходного процесса представлен на Рис. 3.

В дальнейшем был использован ин- струмент для оптимизации – Response Optimizer. Результаты его применения, для K расчета оптимальных коэффициентов p

^KD и ^{KI .} представлены на Рис. 4. и Рис. 5.

В данном случае было проведено 6 итераций.

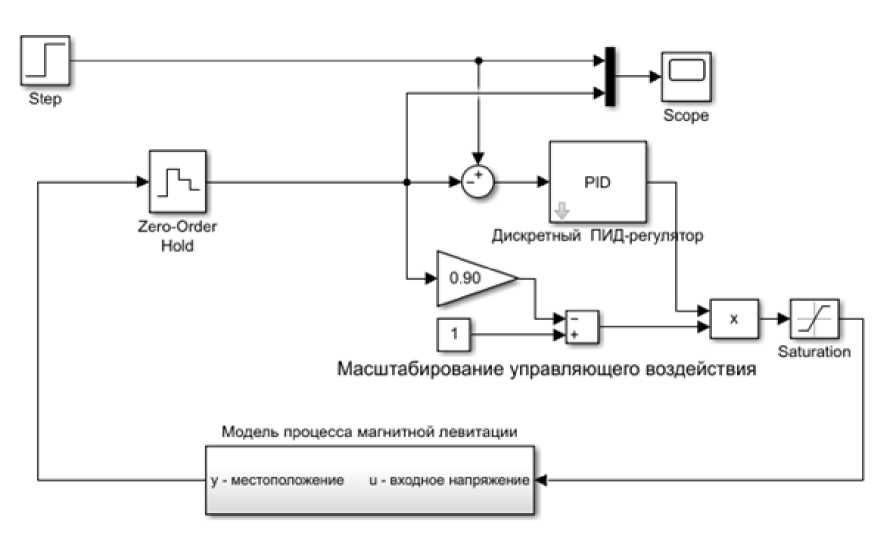
Рис. 2. Simulink-модель процесса магнитной левитации

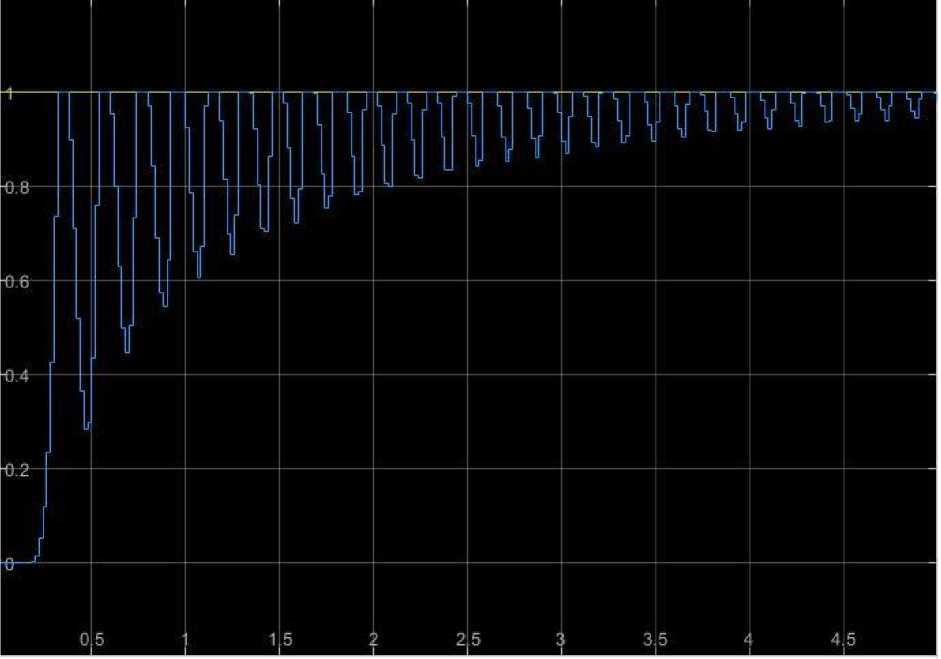
Рис. 3. Переходной процесса с начальными данными

Iteration	F-count	Модель процесса магнитной леви... (^0)	Модель процесса магнитной леви... (>=Ф
0	7	-0.0270	-0.6501	А
1	14	-0.0332	-0.6513
2	21	-0.0270	-0.2406
3	23	-0.0270	-0.0461
4	35	-0.0270	-0.0075
5	42	-0.0270	-0.0020
6	49	-0.0270	3.1846е-06
				V

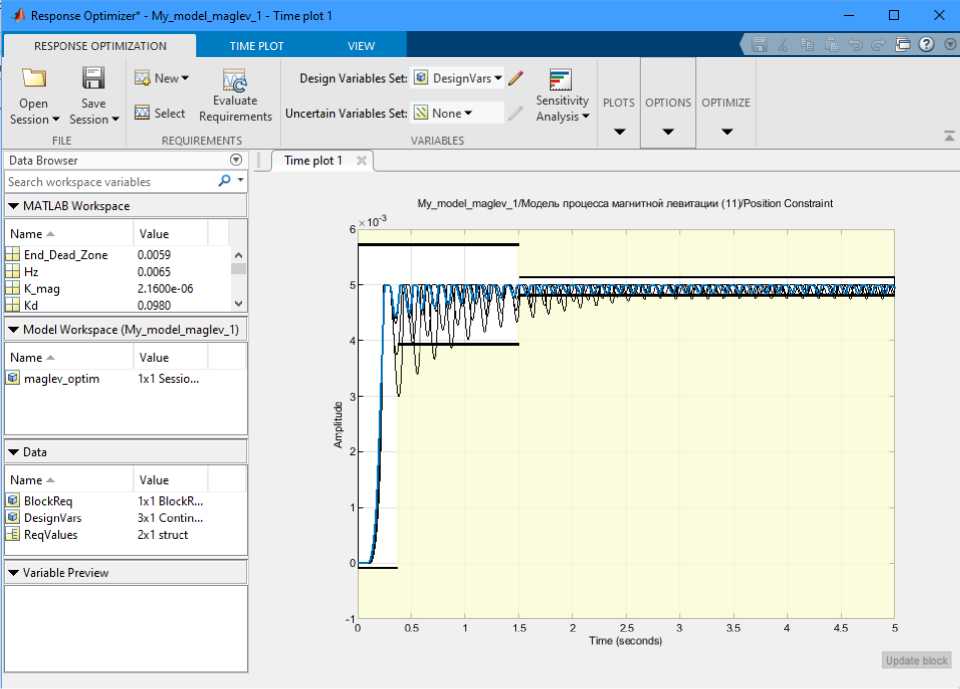
Рис. 4. Работа инструмента Response Optimizer

Optimization started 13-Dec-2021 11:28:21

Optimization converged, 13-Dec-2021 11:28:48

Optimized variable values written to 'DesignVars' in the Design Optimization wortspace

|jSave iteration,,j| Display Options..

Optimize

Рис. 5. Отчет о процессе расчета оптимальных коэффициентов

По окончании процесса расчета, были получены следующие значения:

K p = 0.6215; K = 0.098; K = 8.2791.

График переходного процесса с этими значениями представлен на Рис. 6.

Как видно из Рис. 6, переходной процесс очень быстро приходит в “устано-

вившийся” режим. Кавычки означают действие теоремы Ирншоу, которая “не дает” системе перейти в установившийся режим.

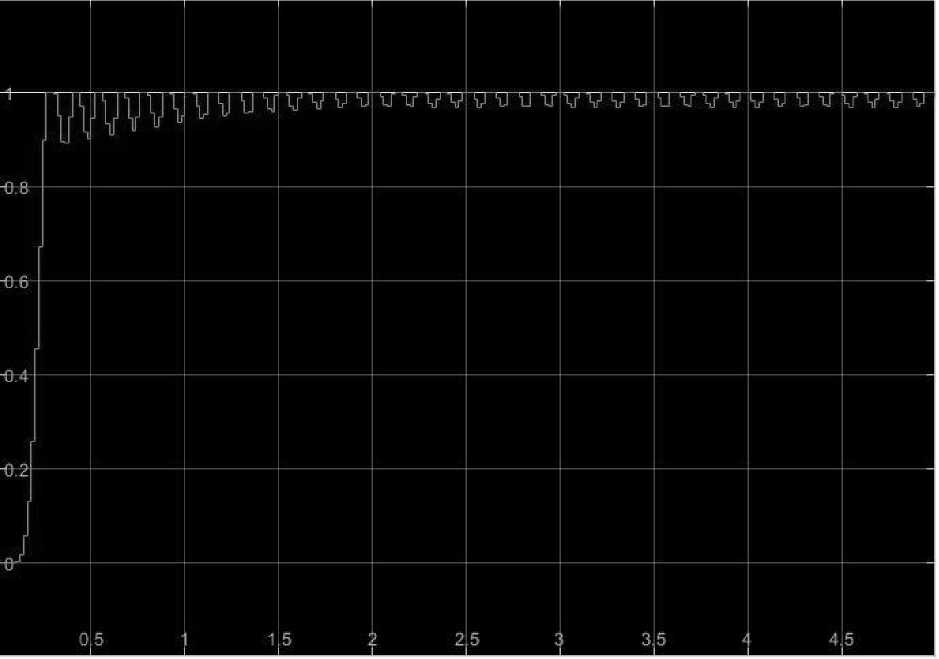
Рис. 6. Переходной процесса с рассчитанными значениями ПИД-регулятора.

Заключение

В рамках работы была разработана нелинейная ММ процесса магнитной левитации. Ее анализ показал, что данная ММ является неустойчивой. Этот факт полностью согласуется с теоремой Ирншоу. Поэтому для регулирования положения ЛТ необходима САУ, позволяющая решить задачу регулирования положения ЛТ в рабочей точке. Для этого была проведена

разработка ММ и исследование в рабочей точке для такой САУ. В качестве системы управления был выбран ПИД-регулятор. При помощи соответствующих инструментов, содержащихся в системе MATLAB, были рассчитаны оптимальные коэффициенты для этого регулятора. Полученные результаты представлены в виде аналитических зависимостей и графиков.