Проектирование мобильных машин моделированием динамических нагрузок на узлах их приводов

УДК 629.01                                                

Mobile machine design through dynamic load simulation on their drive units

S. A. Partko, L. M. Groshev, A. N. Sirotenko

Don State Technical University (Rostov-on-Don, Russian Federation)

Introduction. The mobile machine design is impossible without considering the vibration parameters of their units. This requires the development of specialized dynamic models that take into account the probabilistic nature of these parameters. The root cause for the occurrence of vibration effects is the profile irregularity of the mobile machine path, and the variability of physicomechanical characteristics of the soil. Problems that consider these features are solved linearly with sufficient accuracy; but in multidimensional dynamical systems, such an approach is unacceptable due to the presence of a large number of interrelationships. The work objective is to conduct a comparative analysis of the efficiency of existing calculation methods of statistical characteristics of uncorrelated external actions as applied to a mobile machine presented as a multidimensional dynamic system with actions having different correlations.

Materials and Methods. External actions in the multidimensional dynamical systems are considered in a matrix form. When calculating statistical characteristics, intercouplings in the spectral density matrices are taken into account. The elements of the main and secondary diagonals are determined; the correlations between the effects are taken into account. These features significantly complicate the calculations. So, to get matrices of uncorrelated actions, the matrix of external actions is reduced to a diagonal form.

Results. A numerical comparison of spectral densities and intensity of the mobile machine oscillations under variation of speeds and nature of the soil fertility microprofile was carried out using various methods of calculation. Certain characteristics of spectral densities and oscillations of mobile machines of agroindustrial complex enabled to develop recommendations on the practical application of the presented dependences for designing this machinery.

Discussion and Conclusions. The results of solving the matrix of spectral densities of external actions by various methods are presented on the diagram of spectral oscillation velocities. The analysis of characteristic curves has shown that the identical results, regardless of the calculation method, are obtained only for machines with weak functional relations under the uncorrelated external action of the soil fertility. For some cases, the resonance machine speeds are set. The effect of irregularities of the soil fertility on the oscillation intensity of the machine units and the dispersion of loads on the units is shown in the graphical representation.

Введение. При проектировании надежной мобильной техники необходимо учитывать не только статические, но и динамические нагрузки. На характеристики динамических нагрузок значительное влияние оказывают колебания машины и ее узлов. Учет и определение колебательных параметров требуют разработки специализированных динамических моделей, рассматривающих эти параметры в аспекте вероятностного анализа. Основная причина возникновения колебательных воздействий обусловлена неровностью профиля пути мобильной машины и непостоянством физико-механических характеристик агрофона. С достаточной точностью задачи, учитывающие эти особенности, решаются линейно, что недопустимо при решении многомерных динамических систем с большим количеством взаимных связей.

Материалы и методы. На качество технологического процесса, выполняемого мобильной сельскохозяйственной машиной, влияют как характеристики ее рабочих органов [1–5], так и характеристики ходовой системы [6, 7] и микрорельеф агрофона [8, 9]. В общем случае внешние воздействия на машину рассматриваются как система с n функциями. Процессы изменения микронеровностей пути (или изменения плотности почвы) обозначим как функции q1(0 ... q_n (t) [9, 10].

Если статистическое описание внешних воздействий допускает стохастическое ортогональное представление, то справедливо уравнение:

qi(t) = m[qXt)]+ J й(ю)-ф,-(t,»)dю,

-да где Qi(ω) — система случайных функцийω; φ i (t,ω) — система неслучайных функций t и параметра ω; m [qi(t)] — математическое ожидание.

Мобильные машины АПК — это системы с запаздывающими воздействиями [2, 6, 9], которые характеризуются многими параметрами неровности микрорельефа поля или твердости почвы [2, 8, 9]. Эти параметры являются однотипными и могут быть сдвинуты во времени t 0 . Помимо этого, конструкция машины (колеса переднего и заднего моста) влияет на взаимосвязь между воздействиями. С учетом этих особенностей и предположением, что математическое ожидание внешних воздействий равно нулю, матрица спектральных плотностей внешних воздействий описывается следующим образом [11, 12]:

S h ( to )

S q ( to , j to ) = S h ( to ) e t 0

S h и e - j " t 0

S h И

c 31 S v h ( j ^to)    c 32 S v h ( j ® )

c 13 S h v ( j to )

c 23 ^S h v ( j ^to) ,

^S vW

где с13 = t; c23 = e jtot0; c31 = 1; c32 = ejt0 — для переднего ведущего моста; c13 = e jtot0; c22 = 1; c31 = ejtot0; c32 = 1 — для заднего ведущего моста.

Для упрощения вычисления статистических характеристик приведем матрицу к диагональному виду, чтобы получить матрицу некоррелированных внешних воздействий. Введем характеристическую матрицу и приведем матрицу (1) к виду:

S q ( to , j to ) -X ( j to ) - E =

Sh (to)-X( jto)

S h ( to ) e^j ™ t 0

c31SVh ( jto)

Sh (to)ejt0 Sh (to)-X( jto) c32 Svh ( jto)

c13 ShV ( jto) c23ShV ( jto) SV (to) -X( jto)

где λ — характеристическая функция; Е — единичная матрица. Характеристическое уравнение представим в виде:

a X ³ ( j to ) + b X ² ( j to ) + c X ( j to ) + d = 0.

Характеристические функции X 1 ( j to ) , X ₂ ( j to ) , X ₃ ( j to ) определялись с использованием формул Кардано [13].

Матрица перехода к новому базису, построенная по координатам векторов X i ( j to ) (при i =1,2,3), определенных из уравнения (3), имеет вид:

T (j to) =

В этом случае обратная матрица имеет вид:

П 11

П 12

П 13

П21

П22

П23

T-1 (j to) =

T ( j to ) I ^T ( j to )|

где T ( j to ) — присоединенная матрица; Т ( j to )| — определитель матрицы.

Искомая матрица определялась по выражению:

Sd ( jto) = T"' ( jto) - Sq (to, jto) - T ( jto) = diag ||S1 ( jto) - S2 ( jto) - S3 ( jto)||

где S 1 , S 2 , S 3 — спектральные плотности некоррелированных воздействий функций комплексного переменного.

Нахождение диагональной матрицы (6) упрощается решением плоской задачи. В этом случае внешние воздействия представим в виде:

Sq (to, jto) =

S h ( to )

S h ( to ) e™t ⁰

Sh (to)e-mt0 Sh (to)

Тогда характеристическая матрица определится выражением:

Sq (to, jto)-X(to)- E =

Sh(to)-X(to)

S h ( to ) e™t ⁰

S h ( to ) e -^m t ⁰

Sh(to)-X(to)

В свою очередь, характеристическое уравнение представим как:

X2 (to)-2Sh (to)-X = 0.                                                  (9)

Откуда корни уравнения равны: X 1 ( to ) = 0, X ₂ ( to ) = 2 S_h ( to ) .

При корне X 1 ( to ) = 0, система уравнений для определения координат собственных векторов имеет

следующий вид:

Sh (to) П11 ( jto) + Sh (to) e-^t0 -П12 ( jto) = 0 .

Задавшись Пн = e ^- j ™ t ⁰ , находим n ₁₂ ( j to ) = 1.

При корне X ₂ ( to ) = 2 S_h ( to ) , получим систему уравнений:

( ^- S h (^to)^- П 21 ( ^{j to})⁺ S h (^to) ^{e -} j “ t ^{0 -} П 22 ( ^{j to}) = ⁰

[Sh (to)j“t0 - П21 (jto)+ Sh (to)- П21 (jto) = 0

Тогда матрица перехода к новому базису принимает следующий вид:

Машиностроение и машиноведение

T (j ю) =

e - j ^ю t о     e j ю t о

- 1      e ^{2 j ю} t 0

Преобразованием выражения (8) найдем спектральные плотности некоррелированных воздействий:

S , ( j ю ) = S h ( to ) - (1 + e^j t ⁰ ) = 0.

S2 (jю) = Sk (ю)- (1 + et0) = 0.(13)

Если допустить, что профиль агрофона в продольном и поперечном сечении определен некоррелированными случайными процессами [8, 9], то можно представить третий элемент диагональной матрицы, как S _ю ( ю ) . В этом случае матрица (13) примет вид:

Sd (jю) = diag\\Sh (ю)- (1 + ejt0); Sh (ю)- (1 + ejt0); Sу(ю)||(14)

Решением матрицы (1), совместно с матрицей (14) и с учетом формул, описывающих некорреляционные воздействия, определялись спектральные плотности колебаний. В итоге получилось выражение:

Sz (ю) = Sh (ю)[ф2, (ю) + Ф,22 (ю)] = 0.(15)

Результаты исследования. На рис. 1 представлены графики спектральных плотностей вертикальных скоростей передней части молотилки комбайна семейства «Вектор». Очевидно, что динамические параметры машины влияют на спектр колебаний (рис. 1). Узкополосный спектр характерен для условий близкого совпадения частот собственных колебаний мостов комбайна с жаткой (рис. 1). Также на ширину спектра влияет запаздывание воздействий от колес мостов комбайна.

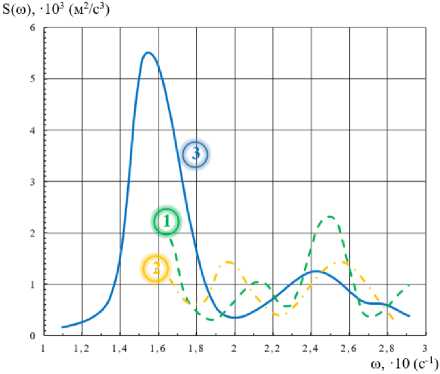
Рис. 1. Спектральные скорости колебаний при решении с использованием: 1 — матрица (1); 2 — матрица (6); 3 — матрица (15)

Результаты расчета интенсивности колебаний с использованием матриц (1), (6), (15) графически представлены на рис. 2, что подтверждает зависимость функциональных связей в машине от характера внешних воздействий.

z/g

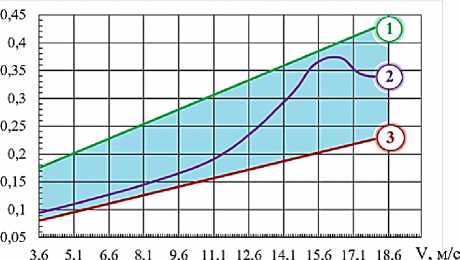
Рис. 2. Графики интенсивности колебаний при движении машины по микропрофилю с различным характером неровностей:

1 и 2 — вдоль борозды; 3 — поперек борозды поля

Решение систем, представляющих собой некоррелированные внешние воздействия на движущийся машины со слабыми функциональными связями, дают близкие результаты вне зависимости от используемых методов.

Одинаковые результаты при использовании различных методов расчетов получаются только для машин со слабыми функциональными связями, при движении по микропрофилю поля, создающего некоррелированное внешнее воздействие.

Оценка динамических характеристик комбайнов производилось по следующей формуле:

^ш 2

W ke = - J S ke И d ® ,                                   (16)

П ш где го 1, го 2 — границы частот спектра.

Интенсивность колебаний для различных условий, определенная с использованием формулы (16), представлена на рис. 3.

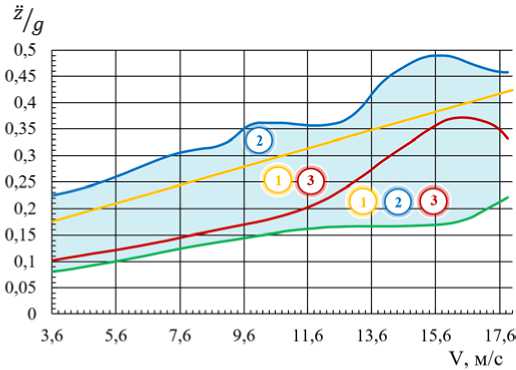
Рис. 3. Результаты инженерной оценки динамики комбайна

На рис. 3 представлены зависимости перегрузок zg от скорости движения комбайна. Очевидно, что различный спектральный состав неровностей микропрофиля агрофона влияет на интенсивность колебаний узлов машины. Следует отметить наличие резонансных скоростей движения в интервале от 10 до 15 км/ч. Полученные графические зависимости (рис. 2, 3) позволяют оценить разброс нагрузок на агрегаты. Затененная область иллюстрирует их рассеивание и позволяет оценить коэффициенты вариации V ( z ). В таблице приводятся параметры распределения нагрузок при средних скоростях движения машин [2].

Таблица 1 Динамические параметры нагрузок для мобильных машин АПК

Тип машины	Режим работы	Скорость движения м/с	z ск g
Комбайн «Вектор»	рабочий	0,840	0,332
	транспортный	2,781	0,835
МТА трактор К-700А, тележка 2 ПТС-4	рабочий	3,352	0,474
	транспортный	8,323	0,510
МТА трактор Т-150А, комбайн ККУ	рабочий	1,247	0,364
	транспортный	3,527	0,382
МТА трактор Т-150А, плуг ПР-2,7	Рабочий (пашня)	0,752	0,346

Обсуждение результатов. Анализ результатов расчетов спектральных плотностей колебаний по формулам (1), (6), (15) графически представлен на рис. 2, 3. Из графических зависимостей видно, что спектр воздействий нагрузок и их динамика оказывают влияние на погрешность вычислений.

Машиностроение и машиноведение

Расчет динамических многомерных систем и оценка колебаний машин автоматизирован и производится с использованием специализированного программного продукта1. Программа применяется для выбора колебательных параметров контуров и агрегатов мобильных сельскохозяйственных машин; расчета плавности хода зерноуборочных комбайнов; для проектирования деталей узлов машин [14]; оценки условий труда механизатора. Перед использованием программного продукта необходимо предварительно выбрать динамическую модель; задаться конструктивными параметрами машины и ее агрегатов; определить массовогеометрические и упруго-диссипативные характеристики системы.

Выводы. Выражения (1), (6), (15) приемлемы для проектировочных расчетов спектральных плотностей воздействий на узлы машины. Использование формулы (6) недопустимо при проектировании машин с режимом движения по неровностям агрофона с низкочастотным спектральным составом и для машин с низкой корреляцией колебаний ходовой и управляемой части.