Проектирование оптических систем с дифракционными элементами на асферических поверхностях

Серьезные успехи в области формообразования, производства оптических пластмасс и изготовления оптических элементов методами прецизионного литья и штамповки открыли возможность массового тиражировать гибридных линз, одна из асферических поверхностей которой несет рельефно-фазовую кольцевую микроструктуру с пилообразным профилем штриха. Включение в оптическую систему таких гибридных линз, одновременно являющихся силовыми и эффективными коррекционными элементами, позволяет значительно улучшать оптические характеристики системы, развивая ее апертуру и/или поле зрения, а также повышая полихроматическое разрешение в заданном спектральном диапазоне [1]. Это, в свою очередь, требует совершенствования методов проектирования оптических систем с такими элементами.

1. Компоновка схемы и получение исходных конструктивных параметров системы

При проектировании оптической системы на первый план выдвигается задача выбора оптимальной исходной схемы, под которой понимают схему, включающую лишь те элементы, свойства и возможности которых необходимы, а количество достаточно для удовлетворения требований, предъявляемых к разрабатываемой системе [2]. Эта задача, названная М.М. Русиновым композицией оптических систем, не решается ни одной из существующих коммерческих компьютерных программ, предназначенных для расчета и проектирования оптики.

Традиционно разработчики оптических систем компонуют исходную схему, опираясь на собственный опыт и используя при этом разработанный Г.Г. Слюсаревым и основанный на теории аберраций третьего порядка [3] аппарат основных параметров P , W , С или, исходя из аберрационных свойств отдельных элементов [2]. Однако наиболее результативным считается подход, при котором исходная схема выбирается из архива известных схемных решений [4].

При разработке же систем, состоящих из элементов, позволяющих осуществлять селективную коррекцию аберраций различных порядков, таких как дифракционные линзы (ДЛ), градиентные или однородные рефракционные линзы (ОРЛ) с асферическими поверхностями более эффективной представляется методика, предложенная в работах [5, 6] и развиваемая в данной статье. Она включает два основных этапа. На первом этапе, исходя из требований, предъявляемых к оптической системе, и учитывая коррекционные возможности элементов различных типов, выбирается ее конфигурация, т.е. общее число элементов, их тип и взаимное расположение. Затем составляется система параксиальных и компенсационных уравнений, решение которой призвано обеспечить заданные параксиальные характеристики и устранение выбранных хроматических и монохроматических аберраций нескольких низших порядков малости. Аберрационные коэффициенты при этом получают на основе диаграммы рассеяния псевдолучей, ход которых через оптическую систему рассчитывается в приближении заданного порядка малости [7, 8]. Общее количество конструктивных параметров при выбранной конфигурации может превышать число решаемых уравнений, и тогда значения свободных параметров определяются из условия достижения минимально возможного уровня остаточных аберраций высших порядков. Поиск набора этих значений включает определение границы начальной зоны поиска, исходя из известных ограничений на значения свободных параметров, выбор шага для каждого из свободных параметров и решение на каждом шаге системы параксиальных и компенсационных уравнений. Результатом этого этапа явится база начальных решений.

На втором этапе для каждого из решений набранной базы при значениях числовой апертуры и полевого угла, близких к требуемым, и оптимальном положении входного зрачка производится расчет хода реальных лучей и вычисляется лучевая функция оценки качества точечного изображения. Затем выделяются решения, для которых значения оценочной функции превышают пороговый уровень. Выделенные решения используются в качестве исходных при последующей лучевой оптимизации. В общем случае, ее осуществляют по положению входного зрачка, коэффициентам радиального градиента всех неоднородных материалов и по полиномиальным коэффициентам ДЛ и асферических поверхностей. При этом оптимизация производится по коэффициентам, влияющим на аберрации, начиная с того порядка малости в аберрационном разложении, который не учитывался при составлении компенсационных уравнений. Если же результаты оптимизации неудовлетворительны (не получено ожидаемое значение апертуры или полевого угла, какие-то конструктивные параметры системы не приемлемы и т.д.), проводится повторное исследование базы начальных решений с изменением условий отбора. В результате окажутся найденными конструктивные параметры, соответствующие предельным для выбранной конфигурации оптическим характеристикам. В случае если эти характеристики не удовлетворяют условиям решаемой задачи, то следует изменить конфигурацию оптической системы, число ее элементов и/или их взаимное расположение, а затем весь процесс поиска повторить.

Оптимизацию целесообразно осуществлять с помощью любой из оптических CAD-систем, позволяющих выполнять трассировку реальных лучей через образующие систему элементы, например, Zemax (ZEMAX Development Corporation) [9] или Code V (Optical Research Associates) [10]. Естественно, что программы, осуществляющие трассировку псевдолучей, в этом случае, должны базироваться на таком же описании элементов, которое заложено в используемом для оптимизации CADе. В связи с этим, ниже остановимся на расчете хода псевдолу-чей через асферические поверхности раздела сред и дифракционные элементы, базируясь на описании, используемом в пакете Zemax.

через такую преломляющую или дифрагирующую поверхность.

Ход реального луча будем описывать в декартовой системе координат, ось OZ которой совпадает с оптической осью. Высоту и наклон луча определим с помощью векторов р и s = d р/ dz ; при этом вектор р имеет составляющие [ x ( z ), y ( z ), 0], а вектор s - составляющие [ e x ( z ), e _y ( z ), 0], где e x и e _y - направляющие тангенсы луча связанные с направляющими косинусами луча соотношениями e = ala и e = a,la - x xz y y z

При распространении луча между k -ой и (k +1 )-ой асферическими поверхностями луч на входе в среду (после преломления на k -ой поверхности) зададим векторами рk и s k , а на выходе из среды [в точке падения на (k +1 )-ую поверхность, но до преломления на ней] - векторами рk+1 и sk+1. Если zk k+1 есть расстояние вдоль оси OZ от точки входа луча в однородную среду до точки его выхода, то очевидно, что векторы рk , sk и, рk+1, sk+1 связаны между собой уравнениями рk+1 = р k + zk,k+1sk , s k+1 = s k.

2. Расчет хода псевдолучей

Расчет хода псевдолучей в однородных средах, ограниченных четными асферическими поверхностями вида

F ( p , z ) = cz - 1 + V 1 — ( c P ) 2 —

^- 1 ° 3 ⁽ c P ^{)4 -} 116 ° 5 ⁽ c P ^{)6 -} - = 0

(где z - координата точки поверхности, отстоящей от оптической оси на расстояние p в системе координат, связанной с вершиной этой поверхности, с -кривизна поверхности в ее вершине, ° 3 , ° 5 , ... -коэффициенты асферической деформации поверхности) и через ДЛ, структура которых размещена на таких поверхностях подробно рассмотрен в работах [11, 12]. Здесь же покажем, как осуществлять расчет хода псевдолучей через четные асферические поверхности наиболее общего вида, используемого, в частности, в Zemax:

2 I

z=—,             +Xaip2i ,           (2)

1 + 71 - (1 + к ) c ² p ² i = 1

где к - параметр эллиптичности, a i - при i = 1,2,3,... коэффициенты асферической деформации. Речь идет о получении выражений, описывающих точку пересечения псевдолуча, распространяющегося в однородной среде, с асферической поверхностью, а также параметров луча прошедшего

Пусть dk - расстояние между вершинами k -ой и (k +1) -ой поверхностей. Тогда zk,k+1= dk + zk+1 - zk ,                             (4)

где z_k - координата точки пересечения луча с k -ой поверхностью в системе координат, связанной с вершиной этой поверхности и, аналогично, z_{k + 1} -координата точки пересечения луча с ( k + 1 ) -ой поверхностью в системе координат, связанной с вершиной ( k + 1 ) -ой поверхности.

Асферическую поверхность, являющуюся границей раздела сред, определим в декартовой системе координат, плоскость XOY которой касается вершины поверхности. В дальнейшем такую систему координат будем называть K - системой. В этой системе координат асферическую поверхность опишем уравнением, полученным путем преобразования выражения (2):

F ⁽ p , z ) = z --              .^- ^ ^a i P ² i = 0, (5)

1 + 71 - (1 + К ) c ² p '²

или

F ( p , z ) =

z

-

(1 + к ) c _

1 - 7 1 - (1 + К ) c ² p

-

- X a i p ² * = 0.

Тогда координаты zk и zk+1 можно опреде лить из выражений

_      1

^Z k   ^{(1 + K} k ) c k

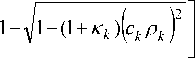
+£dk) Pk1, zk+1 _        П

^{(1 + K} k + 1 ) c k + 1

₊ y _n^{( k + 1}) _n²²

⁺ ^ ^a i    P k + 1 -

⁽ c k + 1 ^P k + 1 )

^ (7)

Уравнения (3), (4) и (7) являются основой для получения формул расчета хода псевдолуча через однородную среду, ограниченную четными асферическими поверхностями наиболее общего вида. Произведя при выводе формул операции, аналогичные описанным в работах [11, 12], для порядковых составляющих расстояния

(0)      „(2)      „(4)

z k , k + 1 z k , k + 1 ⁺ z k , k + 1 ⁺ z k , k + 1 ⁺ ••• ,                  ⁽⁸⁾

получим:

7 (0)

zk, k+1 dk’ z. + _в k+1 - A, k U(2) + A, k+1 dk (2v(2) + dw)

двумя асферическими поверхностями. При этом каждая из этих поверхностей может представлять собой как поверхность оптического элемента, так и любую другую поверхность, например, поверхность предмета или изображения.

Расчет хода псевдолуча через преломляющую или дифрагирующую поверхность сводится к тому, чтобы по известным составляющим различных порядков малости векторов p и s , характеризующих псевдолуч, падающий на поверхность, разделяющую две среды или несущую дифракционную микроструктуру, найти составляющие различных порядков малости вектора s ' , определяющего направление распространения прошедшего (преломленного или дифрагированного) псевдолуча. Решение этой задачи, основанное на использовании закона Снеллиуса или формулы дифракционной решетки, требует знания в частности, составляющих различных порядков малости нормали к поверхности [7, 8, 11].

Вектор нормали к поверхности, описываемой функцией F ( р , z ) , может быть представлен в виде

_ V F

° T(V F )² ,

z k !1 _ в k + 1 — A , k U ⁽⁴⁾ + k k + 1 — A z, k ) U ⁽²⁾ ] ² +

где

+ А_Л + 1 [ d k ( 2 V ⁽⁴⁾ + dp ) + 2 z k 2 k + 1 ( v ⁽²⁾ + dw ) ] +

^ (9)

. д F .9F   д F

V F _ i--+ j--+ k —, дx ду    дz

⁺ в k + 1 d k | ⁴ d k ^[ v ^{(2) ] 2 +} d k w ^{(2) ] 2 +}

+ 4u < ² > v < ² > + 2 d_ku < ² > w ⁽²⁾ + 4 d² v ⁽²⁾ w ⁽²⁾ }

Здесь параметры P i _k и P i _{k + 1} (при 1 _ 1,2 ), относящиеся к k — ой и k + 1 - ой поверхностям, вычисляются по общим формулам

„    1           „               3

Р 1 ^_ — с ⁺ а_ь Р 2 ^_-^{(1 + к} ) с ⁺ а 2 ,

2              8

Произведя дифференцирование выражения (6), введя обозначение

A _ , c , , + 2 £ iap ^{2(1 - 1}>           (15)

V¹ - ^{(1+ k )} c ^p

и, учитывая, что p _ x + у , получим:

а составляющие трех инвариантов вращения

2_,.(2)     (4)        ]

и — p k — U + U + ...,

(2)     (4)

^{V p} k ^s k   ^{V + V +} ...,

W = S 2 _ W ⁽²⁾ + W ⁽⁴⁾ + ...

имеют вид:

u     | p « Д, u _ 2 p k '>p k ”,

V < ² > — p i ", k », V <«>_ p k »₈J> . p (» = (»

w® _ | _E k »]^! , w " _ 2 s p. J ».

Уравнения (9) - (12) позволяют по известным составляющим первого, третьего и пятого порядков малости параметров луча на входе в однородную среду вычислить соответствующие составляющие параметров луча на выходе из нее, т.е. эти уравнения позволяют рассчитать ход псевдолуча пятого порядка через однородную среду, ограниченную дf , дf , дf л

— _ — xA , — _ — yA , — _ 1.

д x        д у         д z

Отсюда

V ( V F ) ² _ V 1 + р ² A ² .

Таким образом, составляющие вектора нормали будут иметь вид:

O x _— xAo z , О у _— yAo z , o z _ V д/1 + P ² A ² . (18)

Для того чтобы получить порядковые составляющие вектора нормали, разложим в ряд радикал д/1 — (1 + к ) с ² р ² и, подставив результат в (6), запишем

F ( р , z ) _ z — Р 1 р ² — Р 2 р ⁴ — Р з P ⁶ — ...,         (19)

где в 1 и в₂ вычисляются по формулам (10), а

Р з _ ^(Х + к ) ² с ⁵ + а з .                     (20)

Дифференцируя уравнение (19), получим:

^F = -2 x в + 2^ Р2 + 3в3 Р4 +...), dx д = -2 у (в + 2^ Р2 + 3в3 Р4 + 4

5 у

= 1.

д z

Далее, используя (11) и введя обозначение Л = в , + 2 в₂ р² + 3в₃ р⁴ = в 1 +2 в₂ ( и ⁽²⁾ + и ⁽⁴⁾ ) + +3в 3 ( и ⁽²⁾ ) ² +..., запишем Л в виде суммы рядков малости

Л = Л⁽⁰⁾ +Л⁽²⁾ +Л⁽⁴⁾ + .. где

Л(0) = в

Л⁽²⁾ = 2 в и ⁽²⁾ ,

Л⁽⁴⁾ = 2 в ₂ и ⁽⁴⁾ + 3 в ₃ ( и ⁽²⁾ ) ² .

Подставляя новую переменную в (17),

V(VF)2 = V1 + 4р 2Л2 ,

откуда

=       1

z   71 + 4 р ² Л²

Аналогичную форму имеют и составляющие o y .

Далее, используя закон Снеллиуса, и преобразования, подобные приведенным в работах [11, 12], для связи порядковых составляющих падающего

£ x =    ₊ £® _{+    +} ...

и преломленного псевдолучей

£ ‘ = £ ‘⁽¹⁾ + £ ‘⁽³⁾ + А 5 + ... , xx x   x

получим

слагаемых различных по-	£ ‘(1) x	= a x <*>,	1
. ,                            (23)	£ x (3)	= a x (1) y (2)	+ a x(3^ ,	(33)
	£ x (5)	= a x 11 у (4)	+ a x (3) y (2) + a x (5).

Здесь

= 1 - 2 ( и ⁽²⁾ + и ⁽⁴⁾ ) х

х"(л(0) )2 + /Л   Л(2) 1 + б(и(2) )2 Л   )4.

		a ( 1) = £ Z1’ , xx
получим		ax 3) = £x3)	-1 £ X 1 ’ e ( 2) , 2 x 1
(25)		a x 5) = £ f	-1 £ (3 ) e :2) +1 £ 2 x 1       2 ■
	а	e 1 (2) и e 1 (4)	составляющие
(26)	e 1	= x 2 + у 2 .

x инварианта вращения

Порядковые составляющие величины

Порядковые составляющие o z имеют вид

оZ0) = 1, о z2 = -2 и(2) Л  )2,

’ (27)

оZ4) = -4и(2)Л(0)Л(2) -2и(4) (Л(0) )2 + б(и(2) )2(Л(0) )4.

eZ4)

’ (34)

,

Y = — = 1 + у ⁽²⁾ + у ⁽⁴⁾ + ...,

a z

входящие в уравнение (33), вычисляются по формулам

/2) = -aу(2), 4 z(2) ]2

а\ ⁽⁴⁾,

где

Учитывая, что

(1)        (3)       (5) p k + 1 =p k + 1 + p k + 1 + p k + 1 + ...	(28)	az (2) = vaZ2)
из выражений (17) и (22) следует		a Z (4) = vaZ4)
о, = -2 x Л ог = -2 ( x (1) + x (3) + x (5) ) х		/ f
xz		V = n I n ,
х ( Л(0) +Л(2) +Л(4) )( 1 + oZ 2) + oZ 4) ) =

-2

+ X

+ X

(0)„(2) o_z

(0) o (4)

+ X ⁽²⁾ ,

+ X(2) о z2) + X(4),

( x «Л⁽⁰⁾ + x ⁽¹⁾Л⁽²⁾ + x ⁽¹⁾Л⁽⁴⁾ + x ⁽³⁾Л⁽⁰⁾ +) х

Ч x ⁽³⁾Л⁽²⁾ + x ⁽⁵⁾Л⁽⁰⁾                       J

х ( 1 + о ™ + о Z ⁴⁾ ) ] + ...

В результате порядковые составляющие ox имеют вид о® = —2 x (1)Л(0),

X

X

X

(0) = 1 - v (0) ,

(2) =- V B(2) X (0) ,

(4) =- VX (0) Гв (4)

В(2) = о

+ о

1 V

о? =

о ?>=-2

x «Л^ о Z ²⁾ + x ⁽¹⁾Л⁽²⁾ + x ⁽³⁾Л⁽⁰⁾ ) , x ⁽¹⁾Л⁽⁰⁾ oZ ^4, + x ⁽¹⁾Л⁽²⁾ о ™ + x ⁽¹⁾Л⁽⁴⁾ + x ⁽³⁾Л⁽⁰⁾ о ™ + x \ ² + x Л⁽⁰⁾

В(4) = о

■ . a ^ xx

+ о

- У*)а 0) + a f’ + o Z ²’, - x*> a Z ³’ + о (3>а О» +

+ о a + о ( ² ’ a <²⁾ + a ( ⁴ ’ + о ( ⁴⁾ yy z z z z

•

Аналогичную форму имеют и составляющие £ у .

Таким образом, задача нахождения составляющих различных порядков малости вектора е ' определяющего направление распространения преломленного асферической поверхностью псевдолуча пятого порядка полностью решена.

Рассмотрим теперь, как можно использовать вышеприведенные соотношения для расчета хода псевдолуча через структуру ДЛ, размещенную на асферической поверхности. В ряде программных продуктов, осуществляющих расчет хода лучей через оптические системы, включающие ДЛ (в том числе, в Zemax), их рассматривают как бесконечно тонкие поверхности, вносящие в падающий на них волновой фронт фазовую добавку

I

Ф = z A p²¹ .                             (41)

i = 1

В этом случае, как показано в [13], пространственная частота и направляющие косинусы падающего и дифрагированного лучей связаны соотношениями

« Р ) = ;;^Ld ^Ф ,                           (42)

2п dp axm)=ax a (m) = ay

+ mA д ф 2п д x ’ mA д ф

+ 2п д y,

где A - рабочая длина волны, a m - номер порядка дифракции. При описание структуры ДЛ через фазовую добавку (41) ее фокусное расстояние определяется коэффициентом A ₁ :

f ' =

п

A i A m

а коэффициенты A i при i = 2,3,... являются коэффициентами асферических добавок.

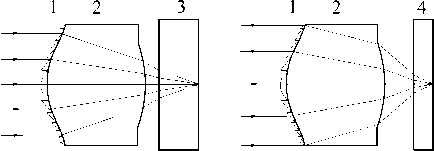
Рис. 1. CD/DVD система объектив – цифровой диск:

1 – ДЛ, размещенная на передней асферической поверхности ОРЛ (2); 3 – CD диск; 4 – DVD диск

Выражения (43) описывают дифракцию на структуре ДЛ в локальной K - системе координат, с направляющими векторами ^~ i , ^~ j , k ^~ , началом координат в точке падения луча на асферическую поверхность и осью OZ ^~ , совпадающей с нормалью o к поверхности в этой точке. Перейти от этой системы координат к K - системе, имеющей направляющие векторы i , j , k и связанной с вершиной поверхности нетрудно обратившись к работам [11, 12].

Затем, воспользовавшись результатами этих же работ, можно получить составляющие различных порядков малости искомого вектора е ' , определяющего наклон дифрагированного структурой ДЛ луча.

3. Оптические системы с ДЛ на асферической поверхности

В работе [14] приведены конструктивные параметры и оптические характеристики разработанного автором рефракционно-дифракционного объектива комбинированного устройства записи и чтения цифровых дисков форматов CD и DVD. Перенос в этом объективе дифракционной структуры с плоскопараллельной подложки на переднюю асферическую поверхность ОРЛ, пересчет исходной схемы по псевдолучевой методике и последующая оптимизация с использованием CAD-программы Zemax позволили упростить конструкцию и снизить массу объектива, не ухудшая качество фокусировки. Оптическая схема системы представлена на рис. 1, а конструктивные параметры исходного решения и значения оптимизирующих полиномиальных коэффициентов A ₄ - A 8 , a 44 ¹ ) - a ^¹ , a 44 ²⁾ - a 82) - в таблицах 1 и 2, соответственно.

Система обеспечивает на длине волны CD-формата A 1 = 0,78 мкм при числовой апертуре А' = 0,51, а также на длине волны DVD-формата A 2 = 0,65 мкм при А' = 0,65 дифракционноограниченную фокусировку в пределах полевого угла 2 ® <  1,4 o . Максимальный световой диаметр линз объектива D _св =3,04 мм. Интенсивность Штреля в сфокусированном пятне не ниже 0,95, а доля энергия в пределах диска Эйри cвыше 83%.

Если при проектировании объектива комбинированного устройства записи и чтения цифровых дисков двух форматов ввиду малого полевого углу и благодаря наличию автофокусировки требуется лишь устранение комы и подавление сферохроматизма, то фотообъективы и, в частности, микрообъективы мобильных телефонов или видеокамер наблюдения, работающие в видимом спектральном диапазоне, требуют, прежде всего, устранения хроматизма положения и увеличения, а затем и сферохроматизма.

Если к тому же учесть, что такие объективы должны формировать плоское изображение в широком полевом угле с высоким разрешением при низкой дисторсии то ясно, что параллельно требуется минимизация всех монохроматических аберраций. Используя совместно предложенную в работе [15] параксиальную методику апохроматизации оптических систем с помощью дифракционнорефракционных корректоров и изложенную выше псевдолучевую методику, была получена исходная схема микрообъектива, состоящего из трех ОРЛ с асферическими поверхностями, у которого на заднюю поверхность первой ОРЛ нанесена рельефнофазовая дифракционная структура.

Таблица 1.

Конструктивные параметры исходной схемы системы объектив – диск форматов CD/DVD

-1 r , мм	d λ 1      , мм d λ 2	n λ 1 n λ 2	α 2 ⋅ 10 2 , мм-3	α 3 ⋅ 10 2 , мм-5
2,2222*			-2,3175	-0,8678
	2,5	1,5735 1,5803
-2,2222			5,6280	-7,9895
	0,5 0,8923
0
	1,2 0,6	1,5735 1,5803
0
s ′ F = 0, f λ ′ 1 = 2,334 мм, f λ ′ 2 = 2,328 мм
∗ A 1 = - 124,0151 мм-2, A 2 = - 50,6478 мм-4, A 3 = -30,3627 мм-6

Таблица 2.

Оптимизирующие конструктивные параметры системы объектив – диск форматов CD/DVD

Тип коэффициента	Значения полиномиальных коэффициентов с номерами i = 4….8
	4	5	6	7	8
Ai	27,4803 мм-8	5,1218 мм-10	-29,3343 мм-12	17,5824 мм-14	-3,1397 -мм-16
α i (1)⋅ 10 4	9,007 мм-7	33,8485 мм-9	-68,5371 мм-11	38,4375 мм-13	-7,1092 мм-15
α i (2) ⋅ 10 4	1083,04 мм-7	-942,56 мм-9	471,75 мм-11	- 124,48 мм-13	13,4746 мм-15

Оптимизация исходной схемы с использованием CAD-программы Zemax позволила получить дис-торсирующий план-апохромат, который при относительном отверстии 1:2,4 обеспечивает разрешение 98 мм^-1 при контрасте не ниже 0,5 в пределах полевого угла 2 ω ≤ 60 ⁰ . Остаточный хроматизм положения в диапазоне от λ _min = λ _F = 0,48613 мкм до λ _max = λ _C = 0,65626 мкм не превышает 7,5 мкм, а дисторсия - <0,5%.

Оптическая схема объектива представлена на рис. 2, а конструктивные параметры - в табл. 3, соответственно.

Заключение

Приведенная в настоящей статье методика, базирующаяся на трассировке псевдолучей, позволяет получать конструктивные параметры исходных схем оптических систем, включающих дифракцион- ные структуры, выполненные на четных асферических поверхностях наиболее общего вида. Включение в оптическую систему рефракционных линз с размещенной на асферической поверхности дифракционной структурой, позволяет упростить конструкцию системы и, скорректировав как хроматические, так и монохроматические аберрации, улучшить основные характеристики системы.

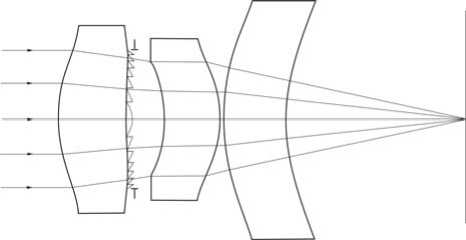
Рис. 2. Принципиальная оптическая схема объектива

Таблица 3.

Конструктивные параметры микрообъектива

r , мм	d , мм	Среда	α 2 ⋅ 10 2 , мм-3	α 3 ⋅ 10 2 , -5 мм 5	α 4 ⋅ 10 2 , -7 мм 7	α 5 ⋅ 10 2 , -9 мм
1,7319			-2,2695	-3,5615	0,2676	-2,7021
	0,76	ПММА
3,9729*			-6,1431	-16,0129	-3,5652	8,5846
	0.4425
-1,6791			2,1514	-21,8536	17,5853	10,6459
	0,6365	ПММА
-1,3310			5,3303	3,6462	4,1340	6,7561
	0,05
2,0066			-14,6056	8,4726	-2,5418	0,4269
	0,70	ПММА
1,5455			-18,7189	5,7059	-1,7250	0,0791
s ′ = 2,056 мм, f ′ = 3,712 мм
∗ A 1 = - 107 мм-2, A 2 = 43,9432 мм-4, A 3 = -493,716 мм-6, A 4 = 2909,23 мм-8, A 5 = -7311,63 мм-10, A 6 = 8711,57 мм-12, A 7 = -4461,27 мм-14, A 8 = 551,757 мм-16