Проектирование полосковой линии передачи

• 1    Расчет параметров полосковой и микрополосковой линии

  • 1.1    Вывод формулы для расчета импедансов полосковой линии

Полосковые и микрополосковые линии передачи играют важную роль в технике СВЧ. Они объединяют блоки СВЧ в одно целое, служат элементами фильтров, полосковых антенн и резонаторов.

Рассмотрим микрополосковую линию передачи с электрическим экраном. Структура такой линии приведена на рисунке 1.1.

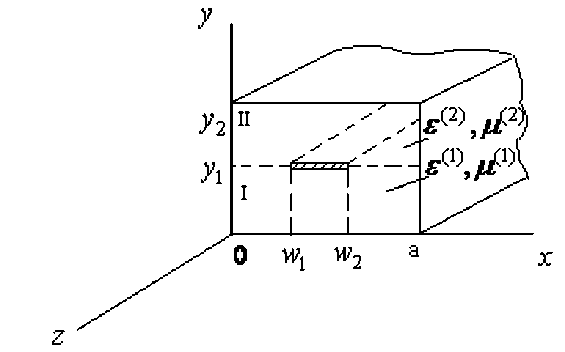
Рис. 1.1- Симметричная полосковая линия в металлическом экране

Сделаем некоторые допущения:

• 1)    ЛП в каждой области является однородной и регулярной.

• 2)    Экран и токопроводящая полоска являются идеально проводящими ( δ =∞ ).

• 3)    Полоска бесконечно длинная и тонкая.

Волна изменяется вдоль оси Z по закону

F(x,y,z)=f(x,y) • e-ihz где h = 2п - постоянная распространения i2 = -1 (мнимая единица).

Граничные условия (ГУ) с учетом того, что экран и полоска идеально проводящая можно записать следующим образом:

при у = 0, у =У 2 ,	дHz E z = 0, Ex = 0,     z = 0, д y
при x = 0, x = a	дHz E z = 0, E y = 0,    z = 0. д x

Граничные условия (ГУ) при у = у 1 запишутся следующим образом:

I       II    I       II Ex  Ex , Ez  Ez , при x ^[W1, W2 ] - полоски, а на полоске Hx - Hx = Jz, Hz - Hz = J,, где J - плотность тока на полоске

Будем полагать в первом приближении, что | J z | >> | J x |, то есть J_x « 0

Тогда ГУ можно переписать в виде:

hI - hI = jx x  xx HI - Hz - 0, т.е. считается, что волна квази- плоская.

Основой макроскопической электродинамики СВЧ является система уравнений Максвелла (в гауссовской системе единиц):

1	'  -  1 дD - — rotH =----+ j + j c   д t         A —                       (1.1) 1 д B rotE =---- c   д t

совместно с уравнениями, связывающими между собой вектора D и E , B и

H , j и E :

D = ⁸a^

bB = H a H                               (1.2)

^ у = аЕ

Будем записывать дальнейшие уравнения, не зависимо от области (к областям перейдем потом). Уравнение (1.2) часто называют уравнениями состояния или материальными уравнениями – они характеризуют среду. Для данной структуры из системы можно получить следующую:

rotH = ik s E

^                ^,                                 (1.3)

rotE = - ik^E где k = — - волновое число. c

Для прямоугольной системы координат получаем из (1.4) две системы скалярных уравнений для составляющих электромагнитного поля:

dH. dy	dH, --y = ik s Ev (1.4.а) x о z	'E^ d y	d E y d z	= - ik H H x	(1.5.а)
d Hx d z	-^ H z = ik s E  (1.4.6) « d x        y	d E x d z	_ dE^ d x	= - ik ^Hy	(1.5.б)
d H y	dH -^H x- = iksE  (1.4.B)	d E y	d E x	= - ik ^Hz	(1.5.в)
d x	d y         z	d x	дd y

Из шести составляющих электрического и магнитного векторов две являются независимыми: Hz и Ez, и потому выразим через них все остальные д E      д H

• — ^l- = - ihE., —i- = ihH_f      (т.к

ii оz         оz

~+ ~ + ihE_y = ik p H x    (1.7.а)

d E

• -    ihE _x —^-z- = - ik ^ H y (1.7.6)

d E_v  QE

• - ---yx = - ik p H z   (1.7.B)

o x    о y

составляющие,     учитывая,     что

E = E ( x,y ) • e - i ^hz,H = H(x,y) • e - ^h ):

^ H z + ihH_v = ik s E    (1.6.а)

дy       yx

• - ihH_x - ^H = ik s E   (1.6.6)

• x    dx        y v7

d H y

—-- = ik s E     (1.6 .в)

z дx

Выражая из (1.6.а) H y и подставляя в (1.7.б) получим выражения для E x

E x

fa H z ( Уу

h

+ pk

•

EEz ) it-)

ike (     pk J

.

(1.8)

Обозначим

kC = (k 2P - h 2)

(1.9)

тогда (1.8) перепишется в виде:

d H_z   h   d E_z

—- +- d y    p k d x ,

Ex = —-- 1-- P k .

ikc или

E x

—

к ² ‘ ^k c L

. a e₇ i^z

—

h H d x

(1.10)

Теперь нужно получить E z и H z , используя волновые уравнения:

'8 X +

dy 2

d ² H z

d ² E z d x ²

d ² H

+ k о E z = 0

.

(1.11)

. d У 2

⁺ d x ²

- + k oO H = 0

Введем обозначения

E = e (x,y ) e

_>— ihz

,

H = h (x, у )e ”ihz.

Каждую из составляющих ех, ey, ez, разложим в ряд Фурье по х на отрезке от 0 до a. Т.к. поля рассматриваем на отрезке от 0 до а (а не на [-a;a]), то остаются или sin или cos в зависимости от граничных условий при х = 0 и при х = а:

e _x

да

= Z e mx ( У )

m n x

• cos-----

e y

e _z

m = 1

да

= E emy ( У )^ sin m=0

да

= Z e mz ( У ) • sin m = 0

a

m n x

a

m n x

a

да hx =Z hmx ( У )• sin"

m = 0

да

^> , (1.12) h ), = Z ^h m>- ( У ) ^ cos

m = 1

да

hz = Z h„ (У )• m=1

m n x

a

m n x

a

m n x cos

a

^ ,  (1.13)

где

1 ^a

ет =   eЛ x,y) • sin В xdx mz        z              m

a0

1 ^a

emx =   e ( Х,У ) * COS в Xdx

mx        x              m

a0

^

h x (^x,y) = E ^h mx ⁽y^{)cos P} m x , m = 0

где введено обозначение

Pm =

mn

a

(1.14)

Подставим разложенные в ряд Фурье ez и hz в (1.11) и, учитывая, что sin и cos на интервале [0; a] – ортогональные функции, получим:

2 emz dy2

d ² h_mz dy ²

² r m e mz

(1.15)

⁺ r m mz

где rm=k2еи - h2 - pm=k0 - pm                (1.16)

Решение последнего однородного дифференциального уравнения второго порядка с постоянными коэффициентами запишется в виде:

I,II        I,II          I ,II           I ,III,II e = A/ cos r y + A, sin r , y mz      1m2

| I,II     i-iIJI         I,II       r>I,II        i,ii ,1'7

h ,  = D , cosr , y + BI  sinr , y mz      1m2

где I или II означают принадлежность к первой области или второй области, соответственно (рис.1.1).

В нашем приближении h mz ≈ 0

Рассмотрим первую область, для которой справедливы следующие ГУ:

III II e = A cosr y + A sinr y = 0 , mz     1m       2m        , при y = 0, eIz = 0 - откуда AI =0, окончательно получим eIz=A 2 sin rIy

(1.18)

По формуле (1.10), учитывая, что hmz ≈ 0, получим h mz

' . W ¹ ) • A ^ r I - cosr I - y .

(1.19)

Из формулы (1.18) найдем emIz sinrmIy

.

(1.20)

Подставляя (1.20) в (1.21), получим

I i • ke( 1 )rIm       I I h =------mc ctgr y • e , mz          2    g m y mz , или при y=y1

II mz   m

I emz ,

где

I i • k^1 )rII

(1.21)

Ym = г rn2 m ctgrmyi формула (1.21) определяет адмитанс 1 - ой области.

Рассмотрим 2 - ую область с параметрами £^, ^^. Для неё выполняется следующие ГУ.

II         II          II          IIII e = A cosr y + A sinr y = 0, mz     1m        2m, при y = y2

II          IIII

Ai =- A2 • tgrmy 2, откуда eIL = AI (cos rI y • sin rI y. - sin rI y • cos rI y.)/cos ry^, = AI sin rI( y. - y.) mz     2        m          m 1        m          m 1          m 2     2      m    21

Таким образом, получаем emIz = A2sinrm(y2 - yi).

Аналогично с 1 – ой областью.

II        II II mz    m mz , где

• t с-2 2 )rⁿ

(1.22)

Ym=ctgrmI2 y 2—У1), адмитанс 2 - ой области.

Напомним, что

[k^ = k ² 8 m ^ 1 - h ²,

V" ]2 = k25<2>„; - h2, к ]2=k v1) ^>

- h2

-

f — 17

к a 7

[ r m ] 2 = k² 8 ⁽²⁾ ^ ⁽²⁾ - hh

fmn 12

к a 7

Разложим ток j _z и j_x в ряд Фурье

^

jz =E Fmz (У )• sin Pmx , m =1

^

jx =Z Fmy ( У )• cos Pmx , m =0

где

2 w 2

^F mz = - f jz(x )^Sin P m xdx ,

a w1

О       ^w 2

F mx

—2— f a( 1 + 5mo)lv jx(x )sin Pmx dx

здесь S m ₀

1, m = 0

0, m ^ 0

Связь между составляющими электрического поля е и F записывается через матрицу импедансов emz

V emx )

= V m i j

К A mz

F mx )

.

(1.23)

Но, учитывая граничные условия, можно записать

mz	—	U11 mx	hmx		\Y Jh m 11	- Y1 Ym 11	у11 Ym 12
mx		hn V mz	-h1 mz )		L Ym 21	Y m 21	Ym 22

^-

-

^I Y m 22

^I Y m 12

^I m i j ,

II m i j      m i j

e mz

V e mx )

.

Введем обозначения

^-

получим:

(F \ Fmz

Y m 11 Y m 12

e mz

F

V mx)

Y Y „ m 21   m 22 J

V emx )

Сравнивая последнюю формулу с (1.24), получим:

[z    ]—[y J-1, m i j       m i j

или

[z  J m i j

где ^A m = ^Y m11 ^Y m 22   Y m 12 ^Y m 21 ,

Y m 22   Y m 21

—

A m A m

Y m 12 Y m 11

—

A m A m

В нашем случае, подставляя вместо

Y ⁽¹⁾ и Y ⁽²⁾ , полученные выше

значения, найдем:

Zm 11 = ik

^ • r m - ctgr mI - У 1    ^ I • r m • ctgr m ¹ • ⁽y 2 - У 1 )

1.2 Вывод интегрального уравнения

При условии, что распространяется квази Е – волна:

E = У e • sin в x = 0 ,                  (1.24)

z         mz         m        , m=1

на полоске при, x g [ w 1 , w₂ ], y = y 1 выполняется e_mz = Z_m1 • F_mz (т.к.

Fmx ~ 0 ), но w2

^F mz =- J jz ( x ) sin P m xdx .

w ₁

Подставляя последнее выражение в уравнение (1.24), получим w2

w

j x Z • sin в x • sin в x dx = 0 • z           mII        m         m

(1.25)

(1.26)

w 1           ^m = 1

J j_z ( x ) K II ( x,x ) dx = 0 .

w ₁

где KII (x,x) - ядро интегрального уравнения mII   у1 _ у II

Y m ^Y m

K II ^{( x,x}' ) = E ^Z mII sin P m x • sin P m x ' • m = 1

• 1.3    Решение дисперсионного уравнения

Не вдаваясь в подробности решения уравнения [1,2] (1.24), указываем,

w что от ряда Kn (x,x' )=E Zm 1j sin вx • sin^nx  нужно отнять t, для улучшения m=1

mn определимости ряда, где t = hm ---Zm m ^w

Затем вводятся преобразование Швингера cos — = C + SU

a

ⁿ ( w i + w ) C = cos —------- 2 a

l ( w ₂ - w )

• cos —-------- 2 a

cos — = S + SV , a

l( w + w_?) П w₃ - w.) S = sin -3 ¹    22 • sin _( ^{2    1 2} ,

2 a 2 a

и в первом приближении получается следующее дисперсионное

уравнение:

t • In + 2 0 = 0

S ^,

(1.27)

где

Ґ

Q = е m = 1

_зж mp _{Ч Z}

2 m- 1

^з и a

2 m - 1

чц

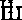
учитывая, что

lim r_m = - im L , Um ctgr_m = - i , получим

m ^w         a    m ^m>

m n

m n

t = lim   a—— = lim — m ^m yi - Y::  m ^m mm ik

Учитывая, что

a

^£ • r m • ctgr m • У 1    ⁶  • r m ‘ ctgr m ' ⁽У 2 - У 1 )

i

-

k l

\ k c Г

. ^L( ^w 2 ^{+ w} 1 )

S = sin —-------- 2 a

• sin

l ( w ₂ - w_x )

2 a

Для симметричных линий

. ^L ( ^w 2 ^{- w} 1 ) S = sin —-------- .

2 a

a

Будем считать, что y 2 = —

aa y1 = 4,     y 2 - y1 = 4

После несложных преобразований дисперсионное уравнение (1.27)

можно записать в виде:

8 ⁽¹⁾

8 ⁽²⁾

-

8 ⁽¹⁾

J

V k 7

-

8 ( ² )

mn

Ю

- 2 L m=1

—

8 ⁽²⁾ ■

П

V k 7

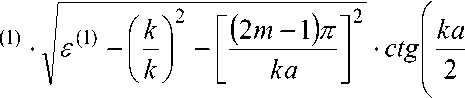
8 ⁽²⁾

—

8 ⁽¹⁾

( h 1 ²

П

>

-

-

V k 7

ka

8 ⁽¹⁾

( k 1 ²

-

-

V k 7

( 2 m - 1 )

m n

( h ) ² r^{( 2 m - 1 ) n} 1 ²

V к 7

ka

ka

■ ctg ^

V

( 2 m

-

-

( h ) ²

V к 7

-

ka

П

Л

-

8 ⁽¹⁾

8 ⁽²⁾

8 ⁽¹⁾

^“

⁽ h ) ²

V k 7

^“

8 ⁽²⁾

^“

( h 1 ²

V k 7

2 m - 1

= 0

(1.28)

• 1.4    Расчет дисперсионных характеристик

Дисперсионная характеристика по уравнению (1.28) рассчитывались в системе MathCAD .

Расчет производится с помощью оператора root и проверяться графическим решением. Для расчета следующие значение у2 = 2, у, = 4, ширина щели ^W = 0.1 • а. Число ряда суммирования N = 20. Графики зависимости

(h. ]

V k 7

в зависимости к • а приведены на рисунке (1.2 - 1.4) при

диэлектрической проницаемости подложки s r = 3,5 и 9,6, соответственно.

4,0000 Г КХ

3,0000

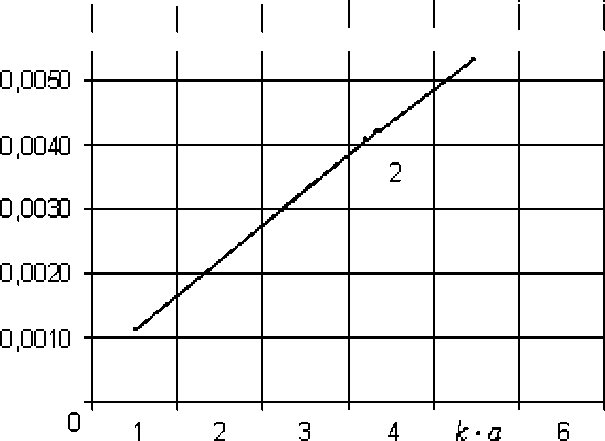
Рис. 1.2- Дисперсионная характеристика ЭПЛ при s r = 3

6,0000 Гй)

5,0000

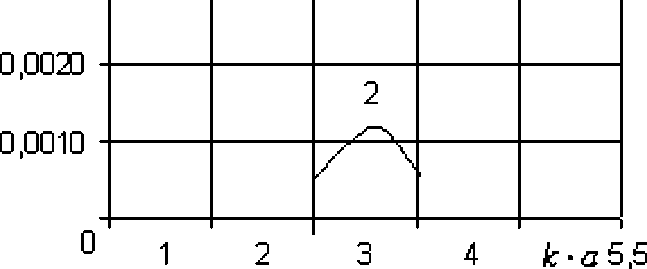
Рис. 1.3- Дисперсионная характеристика ЭПЛ при e r = 5

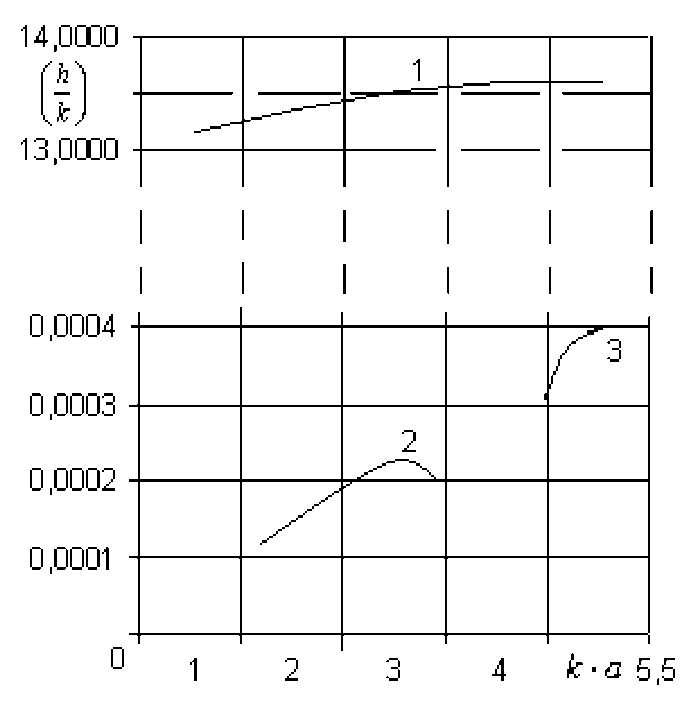
Рис.1.4- Дисперсионная характеристика ЭПЛ при e = 9 • 6

2 Проектирование микрополосковой линии в системе «Microwave Office»

Проведем моделирование полосковой линии в среде «Microwave

Office». Результаты проектирование приведены ниже.

Рис. 2.1 - Топология МПЛ толщиной 1 мм с портами и плоскостями разгерметизации

Рис. 2.2 – Трехмерный вид МПЛ

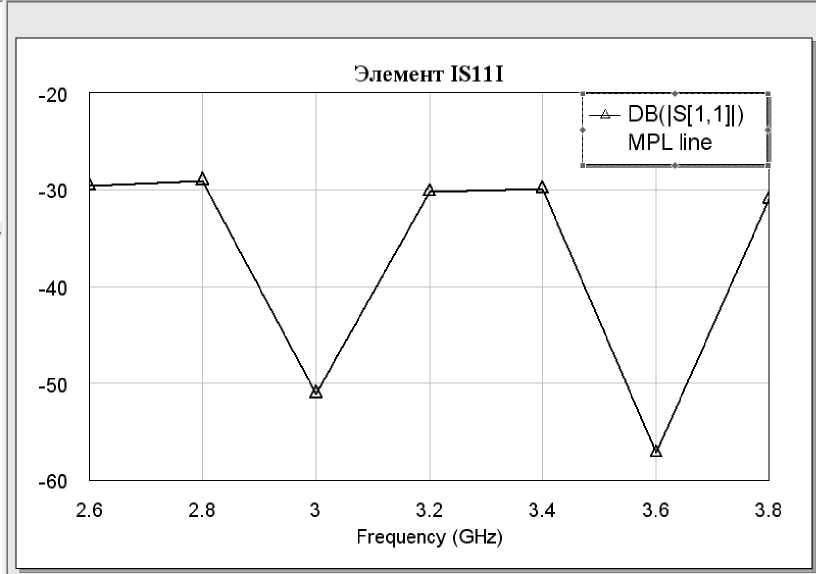
Рис. 2.3- Зависимость элемента S от частоты для МПЛ

толщиной 1мм

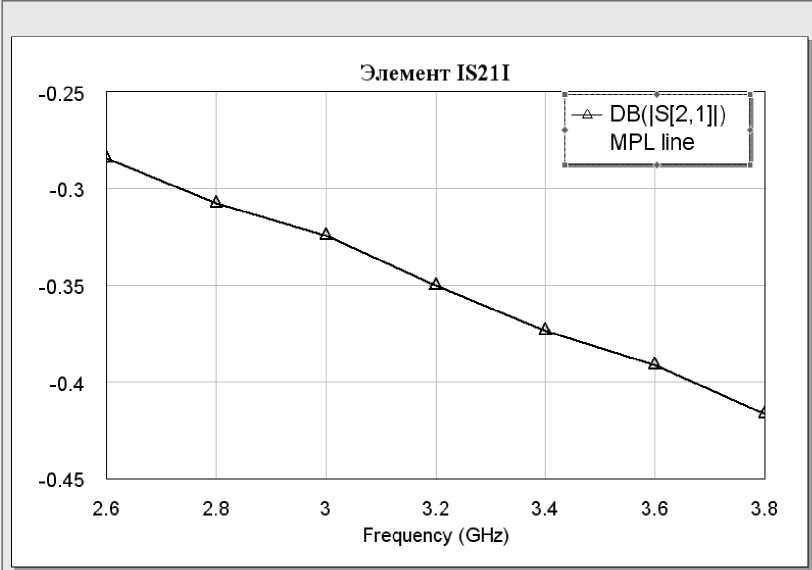
Рис.2.3 - Зависимость элемента S от частоты для МПЛ толщиной 1мм

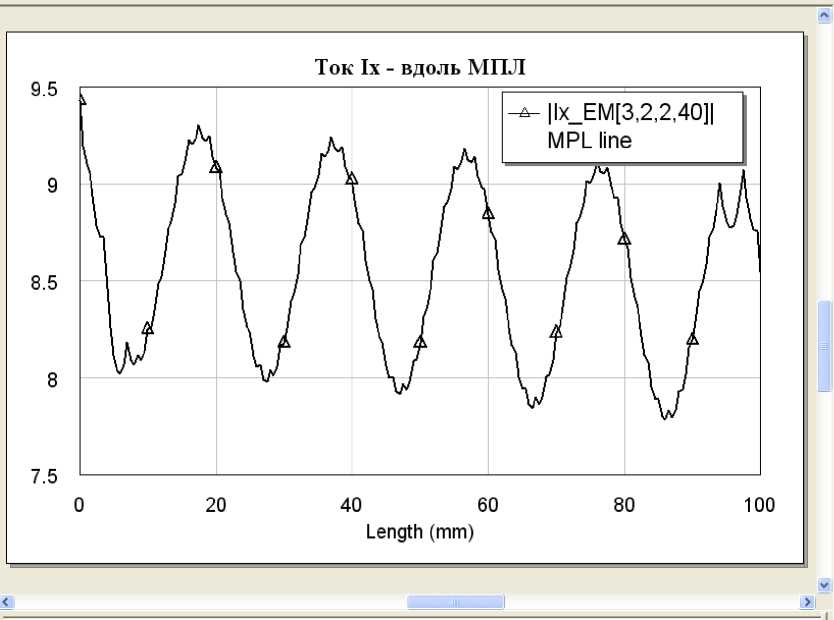
Рис. 2.5 – Зависимость составляющей плотности тока Ix (A/м)

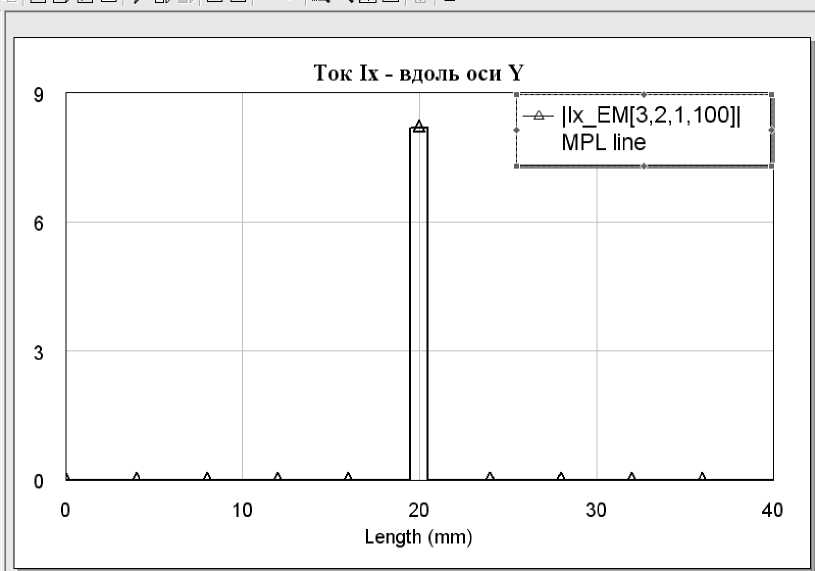
Рис. 2.6 – Зависимость составляющей плотности тока I x (A/м) от частоты для МПЛ толщиной 1 мм вдоль оси Y

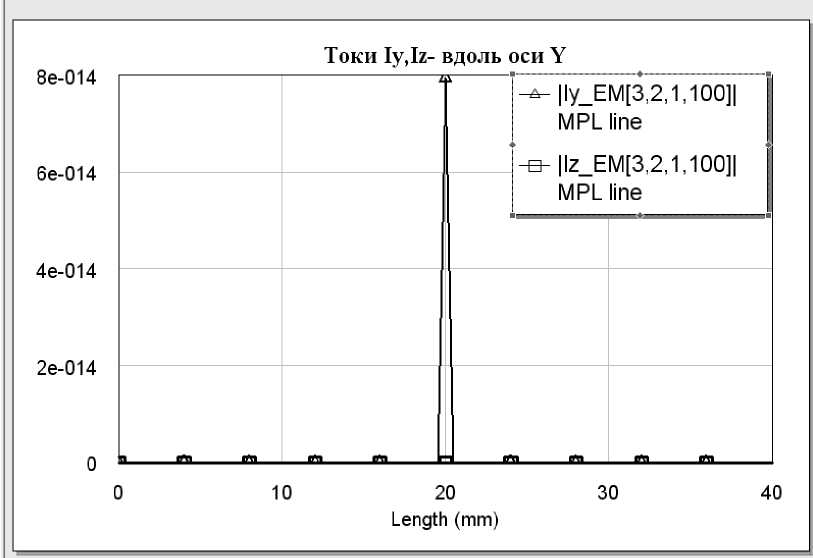
Рис. 2.7 – Зависимость составляющей плотности тока I y (A/м) от частоты для МПЛ толщиной 1 мм (верхний график) и I_z (A/м) –нижний график вдоль оси Y

Как видно из рис. 2.6. и 2.7 , составляющая I x значительно (в тысячи раз) превосходит I_y и I_z. Таким образом, поле в МПЛ формируется за счет x – ой составляющей поля.

Выведем на график КСВН, рассчитываемый по формуле:

• 1    + гД

VSWR(КСВН) =      0 ,

• ¹ - 1 Г 0

где Г 0 – коэффициент отражения порта, с другим нагруженным портом.

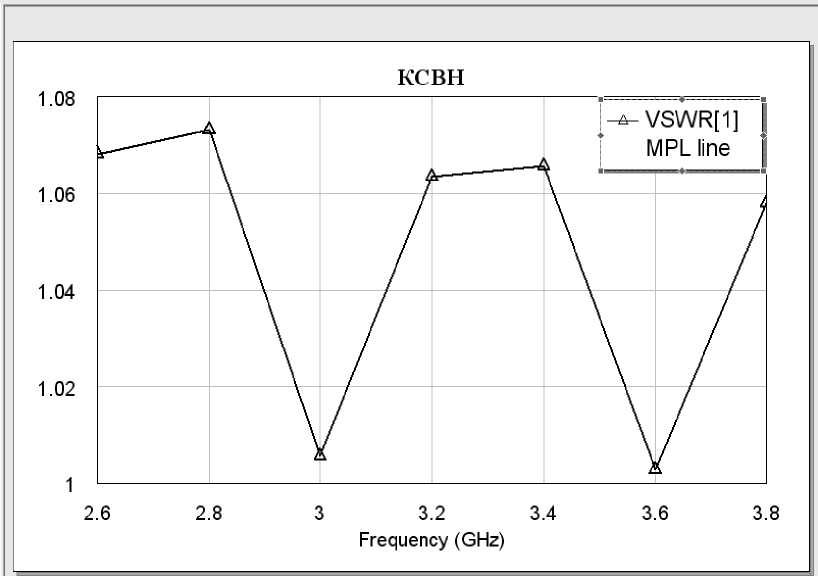
Рис. 2.8 – Зависимость КСВН от частоты для МПЛ толщиной 1 мм

С помощью измерительной линии был измерен коэффициент стоячей волны по напряжению (КСВН) и коэффициент затухания

( дБ ) а —

V м 7

Результаты экспериментальных измерений по сравнению с моделированными в «Microwave Office» приведены на рис.2.9 и 2.11.

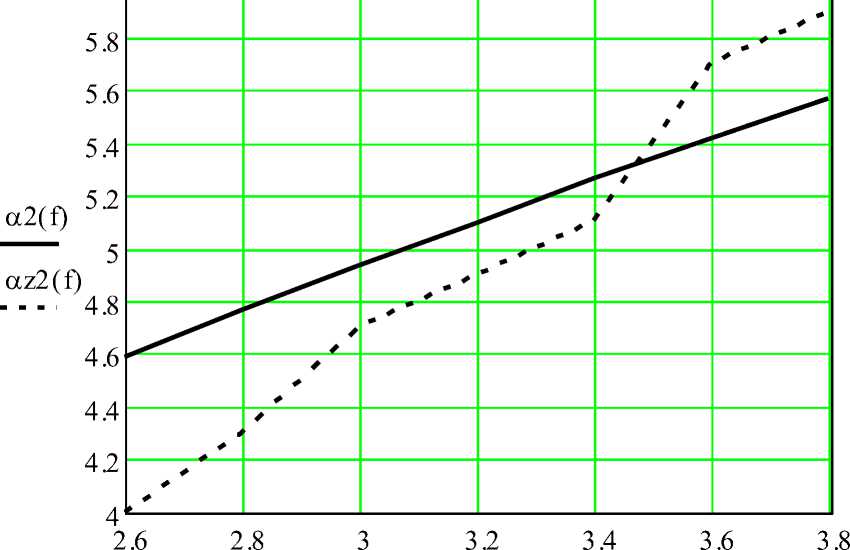
f

Рис.2.9 – Зависимость коэффициента затухания

Г дБ ) а —

V м 7

от частоты

(ГГц) при = 1 : сплошная кривая – теоретическая; штриховая кривая h

– экспериментальная

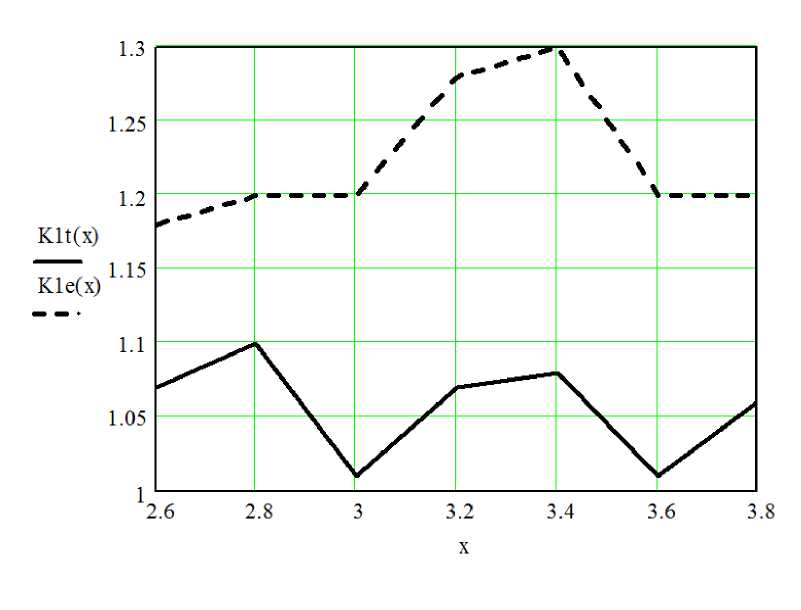
Рис. 2.10 – Смоделированная КСВ (сплошная линия) и экспериментальная КСВ (штриховая линия) для МПЛ 1 мм

K2t(x)

K2 e( x)

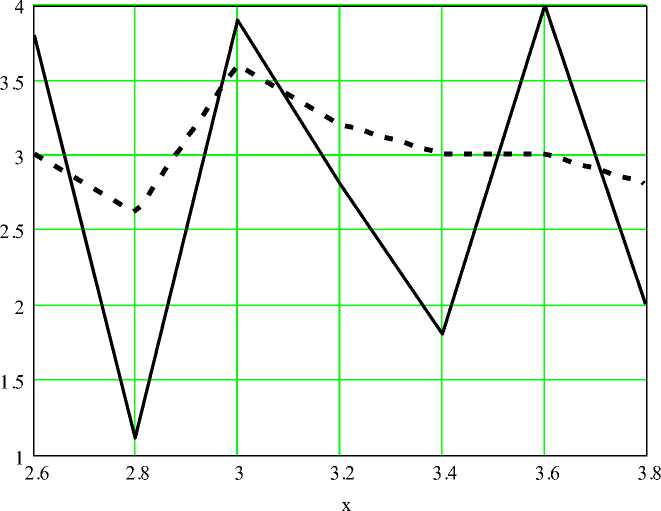
Рис. 2.11 – Смоделированная КСВ (сплошная линия) и экспериментальная КСВ (штриховая линия) для МПЛ 3.5 мм

Как показывают рис.2.9-2.11 расчетные, смоделированные и экспериментальные характеристики достаточно близко совпадают, что подтверждает адекватность полученных формул. Также, полосковые линии можно сначала моделировать на ЭВМ, а потом на основе полученных данных, достаточно точно изготовлять на практике.