Проектирование полосно-пропускающего фильтра на запредельном волноводе

1. Резонаторы на запредельных волноводах.

Анализ работы резонаторов проведем для прямоугольного волновода и для волны типа      но такие же принципы можно применить для рассмотрения работы резонатора в волноводе любой формы при любых волнах.

При возбуждении прямоугольного волновода на частоте выше критической уравнения составляющие поля имеют вид:

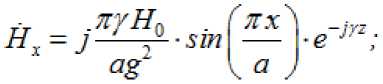
Ё. = 0;

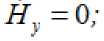
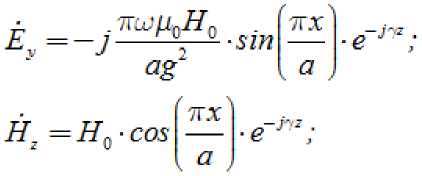
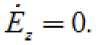
Обозначение осей, размеры поперечного сечения волновода

н

структура поля распространяющейся волны 10 показаны на рисунке 2.2.

и

В уравнении (1) приняты следующие обозначения:

• ^{Н 0} - амплитудное значение магнитного поля в волноводе;

  

  продольное волновое число (вдоль оси Z) или распространения волны в волноводе;

  
  

  постоянная

  
  
  
  
  

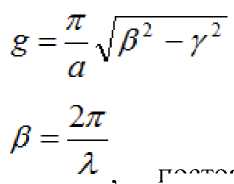
  ,поперечное волновое число;

  
  

  постоянная распространения волны в

  
  

  свободном

  
  

пространстве;

• ω – круговая частота; λ – длина волны в свободном пространстве;

Здесь и далее опущены множители    .

F Н -

Анализ уравнения (1) показывает, что составляющие ¹ и ^х находятся между собой в фазе, а составляющая ^z имеет сдвиг по фазе ^{90 0} относительно ¹.

Вектор плотности потока энергии равный

направлен вдоль волновода в сторону положительного значения оси Z .

При частоте ниже критической имеем:

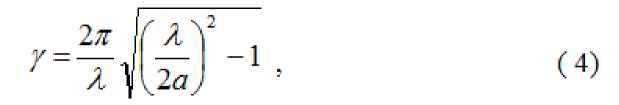
постоянная затухания запредельного волновода, становится действительной величиной.

Уравнение (1) примут следующий вид:

В отличие от распространяющего волновода фазы совпадают и отличаются от фазы ^ на 90 ⁰ .

Вектор плотности потока энергии становится

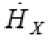
и

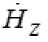
распространение энергии вдоль волновода особенности не распространяющихся полей:

• 1.    Амплитудные поля убывают по ростом Z ;

• 2.    Составляющие магнитного поля и поля сдвинуты на ⁹⁰⁰ (в отсутствие потерь);

• 3. Неравенство энергий связанных между собой электрических и магнитных полей. У волны ^Ю преобладает магнитная энергия.

  

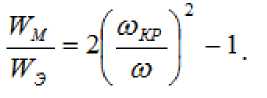
не происходит.

мнимым и

Характерные

экспоненциальному закону с

составляющие электрического

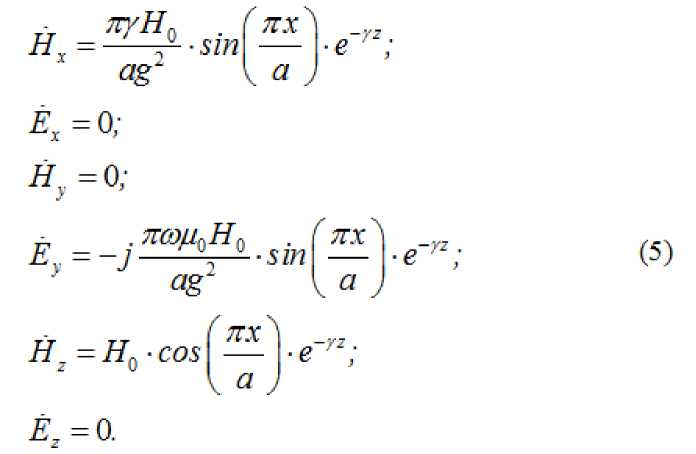
Чем ниже частота по сравнению с критической    , тем больше магнитная энергия по сравнению с электрической.

Фаза колебания электрического и магнитного полей в запредельном волноводе не зависит от координат Z .

В связи с этими особенностями запредельных волноводов различные неоднородности ведут себя иначе.

Свойствами неоднородности определяются накопленной в ней средней за период электрической или магнитной энергией.

Неоднородности типа резонансное окно, емкостная диафрагма и индуктивная диафрагм на частотах ниже критической становятся индуктивными. Эти неоднородности не подходят для создания резонаторов на запредельном волноводе.

Наиболее подходящим элементом для создания резонаторов на запредельном волноводе является металлический штырь, введенный в волновод параллельно линиям электрического поля. Штырь образует с волноводом электродинамическую систему, эквивалентную колебательному контуру. В отличие от распространяющего волновода, где такой штырь полностью отражает энергию электромагнитного поля, в запредельном волноводе он полностью передает энергию на резонансной частоте. Это определяется фазовыми соотношениями между полями штыря и волновода.

Штырь взаимодействует с близко расположенными областями волновода, а находящиеся в некотором удалении участки волновода служат элементами связи. Локализация поля вокруг штыря позволяет создавать высоко качественные малогабаритные резонаторы, простые в конструктивном отношении.

Резонатор на запредельном волноводе показан на рисунке 2.3, его можно представить как короткозамкнутый отрезок полосковой линии длиной меньше    нагруженного на емкость.

Отрезки запредельного волновода представляют собой трансформаторы с коэффициентом трансформации n равным

е rl

п реактивные сопротивления равны:

Zma = j601g4‘8—

Внутреннее сопротивление генератора численно равны сопротивлению волновода.

и

сопротивление нагрузки

Нагруженная добротность резонатора определяется по формуле:

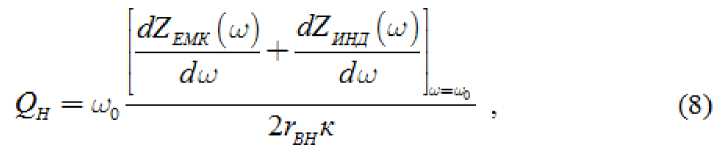
где:

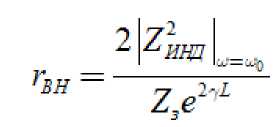
, вносимое сопротивление со стороны генератора и нагрузки;

,

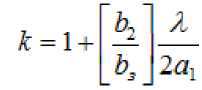
• - коэффициент, учитывающий распределение тока по штырю по сравнению с равномерным распределением. Подставляя эти формулы в (8) получаем формулу (9):

  

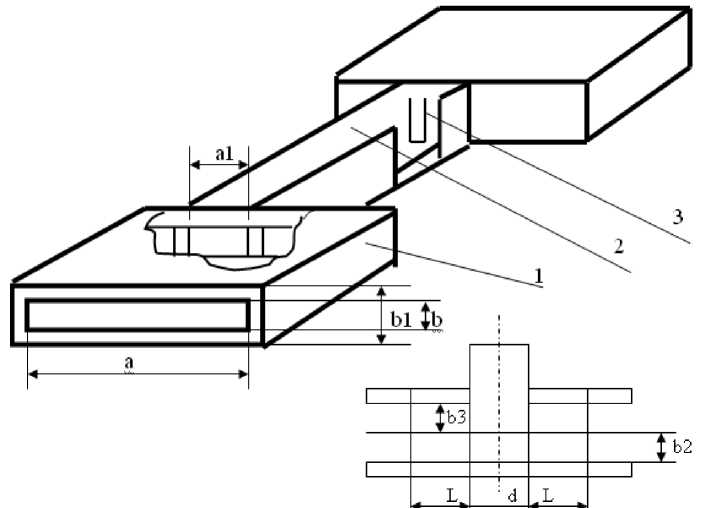
  Рис. 1. Резонатор на запредельном волноводе: 1 – распространяющий волновод; 2 – запредельный волновод; 3 – емкостный штырь

  
  
  
  
  
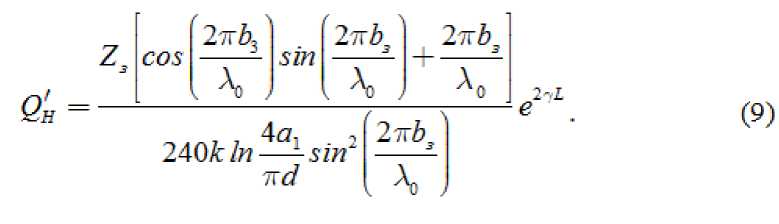2. Расчет резонаторов на запредельном волноводе.

Для учета ослабления связи при стыковке запредельного волновода с распространяющим волноводом, в эквивалентную схему резонатора вводится, дополнительно, трансформатор, с коэффициентом трансформации n1

.

Рассмотрим фильтр со следующими исходными данными:

=сГ1а_х = 9,5 ГГц.

^{а 1} =16 мм; b = 8 мм; d = 4 мм;

где с – скорость света.

Т.е. на частоте f>9,5 ГГц фильтр работать не будет. Значит, рабочая частота лежит в пределах 7,8 ГГц ^ f ^ 9,5 ГГц.

Условие резонанса можно записать следующим образом:

Подставляя в (10) значения из (6) и (7) получим:

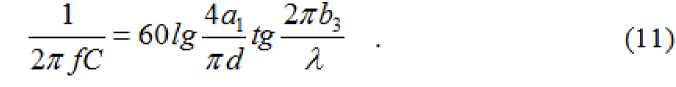
где С – емкость винта в волноводе.

На рисунке 2 изображена емкость винта в запредельном волноводе.

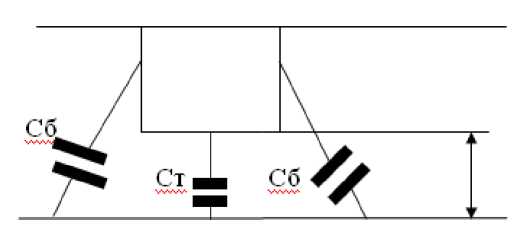
РИС.2.- ЕМКОСТЬ ВИНТА В ЗАПРЕДЕЛЬНОМ ВОЛНОВОДЕ

C = С_т + 2С_б к 3 ^ ТБ_d .

У нас 5=1, f₀= 8,854 10^-12 Ф/м, d^b-b^

Решая уравнения (11) на ЭВМ, меняя Ь_; от нуля до b получаем зависимость f_PE3 от Ь₃ , которая изображается на рисунке 3.

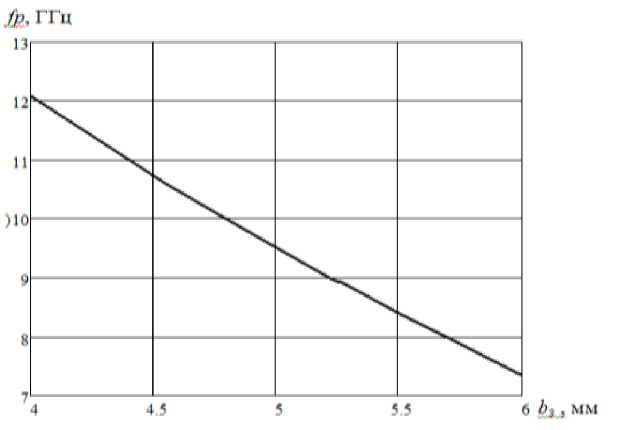
Рис. 3. Зависимость резонансной частоты резонатора на запредельном волноводе от глубины погружения настроечного винта ■ (расчет на ЭВМ).

3. Расчет фильтра на запредельном волноводе

Общие формулы для расчета ППФ на запредельном волноводе

Число звеньев рассчитывается по формуле:

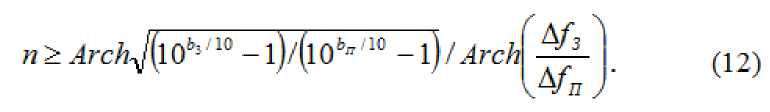
Добротность волноводного резонатора можно подсчитать по формуле

.

(13). В нашем случае колебание имеет тип "101

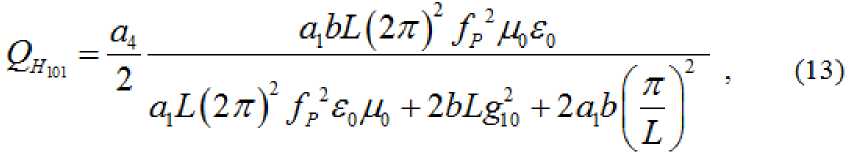
где где

-

магнитная проницаемость материала резонатора, 5 -

проводимость материала резонатора.

Фильтр на запредельном волноводе показан на рисунке 4.

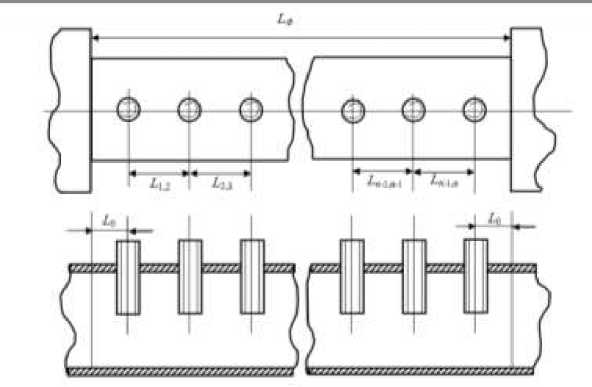
Рис.4. Фильтр на запредельном волноводе Расчет фильтра состоит из двух частей:

-

электрического расчета, в результате требованиям определяется число резонаторов добротности;

которого по заданными n и их нагруженные

-

конструктивного расчета, в результате

которого по известным

добротностям определяются конструктивные размеры фильтра.

5 Конструктивный расчет фильтра

Выбирается размер запредельного волновода и штыря из условия: ^<(1/2 Л); ^<^/4; ^<(0.8^/^).            (15)

С уменьшением ^- по сравнению с ^-г уменьшаются габариты фильтра, но увеличиваются потери.

На практике соотношения объем/потери может быть специально изменено в соответствии с требованиями по потерям.

Зная из электрического расчета нагруженные добротности каждого резонатора, из выражения (9) определяем длины отрезка запредельного волновода :

где

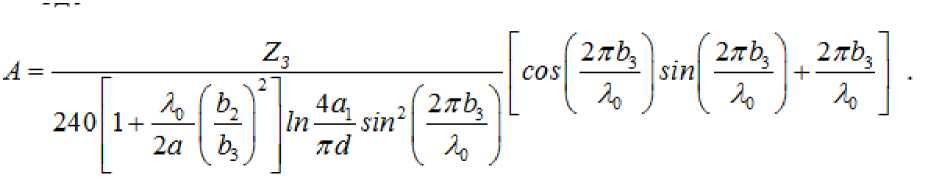
Расстояние между осями штырей:

си вычисляются по формулам:

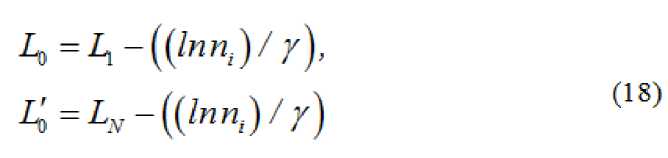
Если фильтр симметричный, то

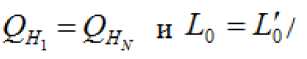
Общая длина фильтра равна:

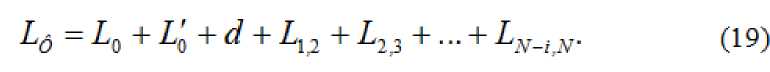
Переходы к линии с распространяющимися волнами должны быть резкими (физически непрерывный переход должен иметь критическое сечение где – то в сужающейся части на всех частотах, для которых волновод меньшего размера является запредельным). Разница в размерах волноводов приводит к ослаблению связи первого резонатора с распространяющей линией, что приводит к необходимости корректировать длину запредельного отрезка по формуле (19).

Возможно соединение запредельного волновода с П – волноводом или волноводом, заполненным диэлектриком, который без диэлектрика является запредельным.

Связь с коаксиальной линией может осуществляться петлей, емкостью и т.д.

6. Расчет ППФ на запредельном волноводе.

Произведем расчет ППФ на запредельном волноводе при следующих характеристиках:

а×b = 23×10 – распространяющий волновод, а1 × b1 =16×8 – запредельный волновод, d=2 мм – диаметр настроечного винта.

По формуле (12) рассчитаем число звеньев, у нас получилось n =4.

Приравняем формулы (17) и (19), меняя на ЭВМ

рассчитываем длину L каждого из четырех звеньев, считая их одинаковыми.

Результаты расчета приведены на рисунке 5.

т _ Г '

По формуле (18) рассчитаем        (рисунок 4).

По формуле (19) найдем общую длину фильтра ^Ф .

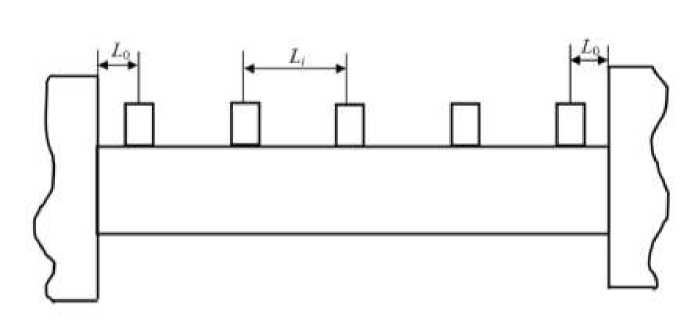
Рис.5. Конструкция ППФ

L_q = L'q =2 мм; Д =15 mm;    L = L^ + L'^ +4 L_t =66 мм.

С помощью программы в среде MathCad были рассчитанны по формуле (16), а “левая часть” – по формуле (19) резонансные частоты.

При совпадении значения правой и левой части находится искомая резонансная частота.

Также была рассчитана зависимость резонансной частоты ^fР от глубины погружения винта ^{b 3} в волновод, которая показана на рис.6.

j и = f 0 = 8.87 ГГЦ – центральная частота нашего фильтра.

Фильтр с заданными в статье характеристиками был измерен на панорамном измерителе P2-61. Данные измерения АЧХ фильтра и КСВ представлены на рисунке 7.

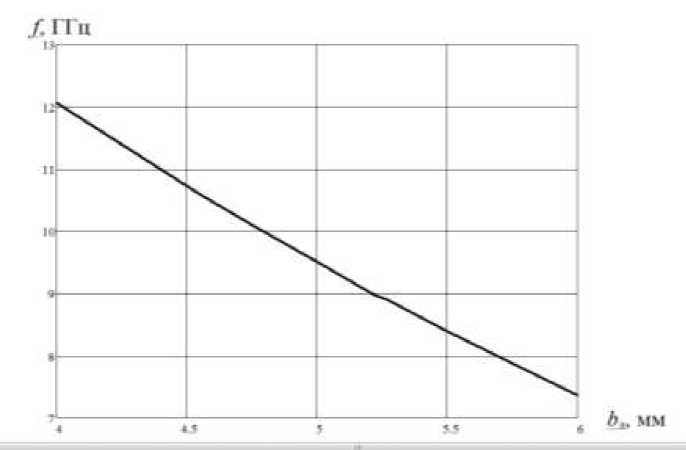
Рис.6. Зависимость резонансной частоты фильтра от глубины погружения винта

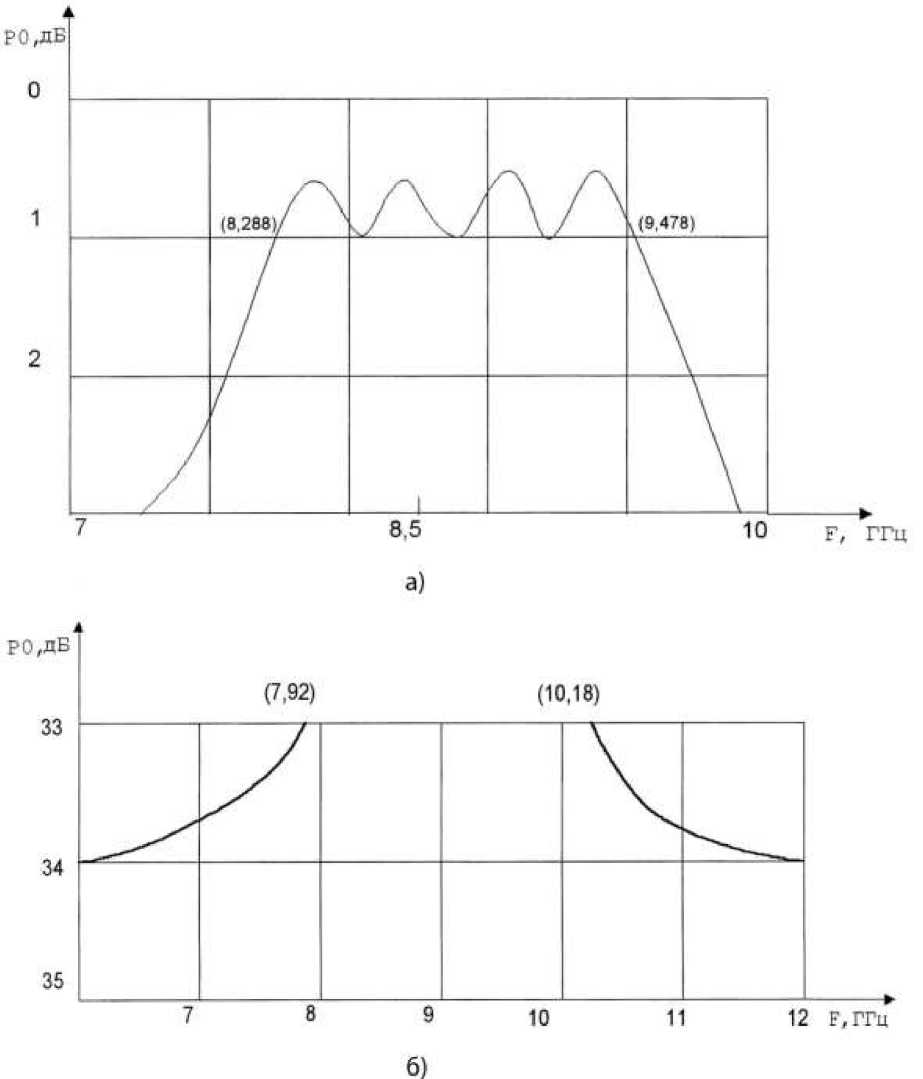
Рис. 7. Фрагменты измерения АЧХ фильтра: а) – верхняя часть фильтра; б) – нижняя часть фильтра.

7. Моделирование ППФ в среде CST Microwave Studio

Для подтверждения расчетных и экспериментальных данных волноводный ППФ был смоделирован в среде CST Microwave Studio.

Смоделированный фильтр представлен на рисунке 8.

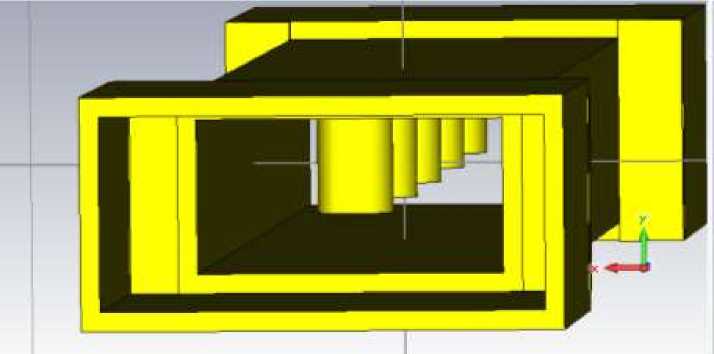
Рис.8. Запредельный волновод со штырями диаметром 2 мм

На рисунках 9 и 10 представлены выходные результаты проектирования.

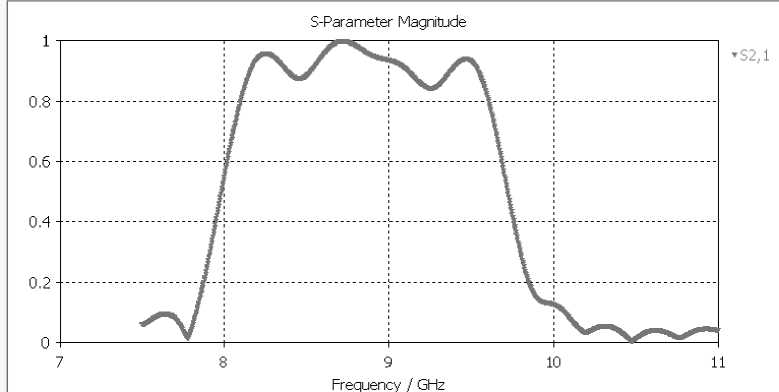
Рис. 9. Зависимость элемента матрицы рассеяния от частоты : диаметры всех винтов 2 мм ,расстояние между винтами 15мм , крайних винтов от большого волновода 3 мм (вся длина 66 мм), глубина погружения винтов 5.1 мм

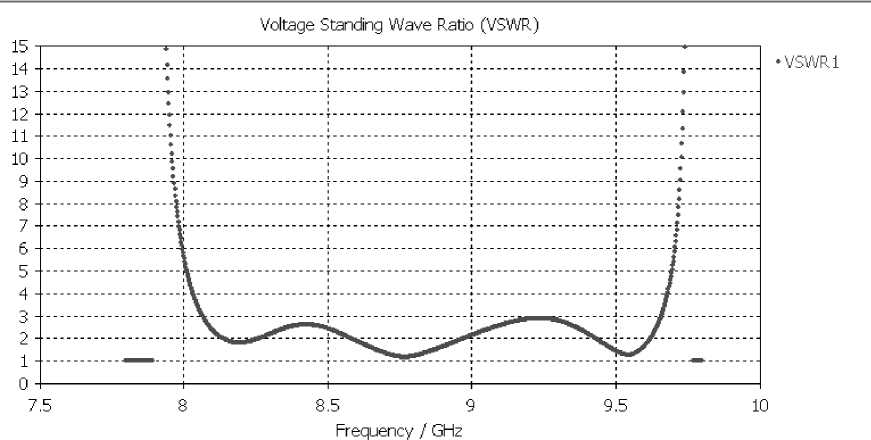
Рис.10. Зависимость КСВ от частоты (остальные данные на рис.9)

Моделирование было проведено по результатам расчетов проведенных выше. Как следует из рисунков 9 и 10, результаты моделирования совпадают с расчетными и экспериментальными данными. Центральная частота порядка 8.9 ГГц, полоса пропускания лежит в пределах 7.8 и 9.7 ГГц.

Результаты исследования таких ППФ и методы их расчета, представленные в статье можно использовать в учебном процессе при изучении курса по электродинамике и СВЧ-устройств.А также, можно применять при инженерных расчетах и проектировании ППФ на запредельных волноводах.