Проектирование предметно-ориентированного языка для расчета специальных функций волновых катастроф

терия, как простота расширения возможностей программного комплекса, поставлена задача о проектировании предметно-ориентированного языка для описания СОДУ, полученных путем вывода из систем канонических дифференциальных уравнений. Разработка специализированного языка, эффективного окружения и среды исполнения данного языка – важная задача при построении систем подобного класса. Интеграция предметно-ориентированного языка в систему позволит упростить процесс добавления программ расчета новых СВК, снизить порог вхождения разработчиков этих программ за счет использования языка более высокого уровня, отделить описание самого процесса вычисления от прочих действий, связанных с взаимодействием со средой исполнения.

Метод систем обыкновенных дифференциальных уравнений и его реализация в программном комплексе

Волновая теория катастроф предлагает целый ряд методов для изучения структурноустойчивых фокусировок. К ним можно отнести метод суммирования рядов Тейлора, метод равномерных асимптотик, контурный метод. Данные методы достаточно эффективны при расчете СВК катастроф с малым количеством параметров. В случае многопараметрических катастроф [3; 4] сложность применения данных методов значительно возрастает.

При разработке программного комплекса было принято решение использовать метод систем обыкновенных дифференциальных уравнений [1]. Данный метод хорошо применим для расчета СВК как простых, так и для многопараметрических катастроф.

Из системы канонических дифференциальных уравнений в частных производных можно вывести систему обыкновенных дифференциальных уравнений. Переход к такой системе приводит к тому, что помимо вычисления самой СВК требуется вычислить ряд ее первых производных.

Решение системы представляется в виде фундаментального вектора (1). Компоненты вектора обладают следующими свойствами: размерность вектора минимальна из всех возможных, все остальные производные СВК V , ( S ) по S i выражаются с помощью линейных алгебраических соотношений:

W = (V , , v ’ , v _z ²,..., V ^{- 1}).                       (1)

В качестве примера рассмотрим особенность A3, СВК которой имеет вид:

+to

V ^ = j exp [ i ( x ³ + X 2 x ² + X ₂x ) ] dx .          (2)

-to

Фундаментальный вектор будет содержать три компоненты: саму функцию и две ее первые производные.

Система обыкновенных дифференциальных уравнений, соответствующая данной СВК, может быть представлена в следующем виде:

dV = V, dL = V - , dV l = iV 2 , d X ₁       d X 2        d X ₁

dV ²

d X 1

= 1(X1V - 2 iX2V') = U 21, dV1=U,, dr: dX2 21, dX2

- -4 (V + x y ¹ + 2 ^ 2 V ²).

Ее дополняют начальные условия: V (0) = 2 ^r( 1 ) exp ( i n /8 ) , V ’(0) = 0, V ²(0) = i r[ | J exp ( i3 n /8 ) .

Графики амплитуды и фазы данной особенности выглядят следующим образом:

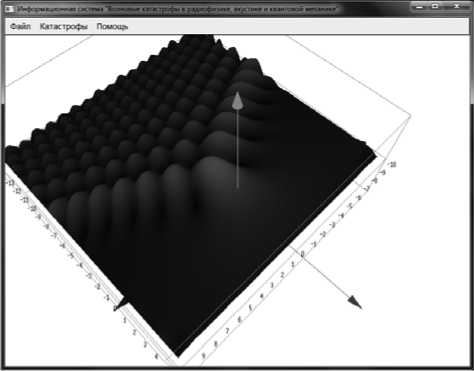
Рис. 1. Особенность А₃, амплитуда, λ ₁ = –15..15, λ ₂ = –10..1

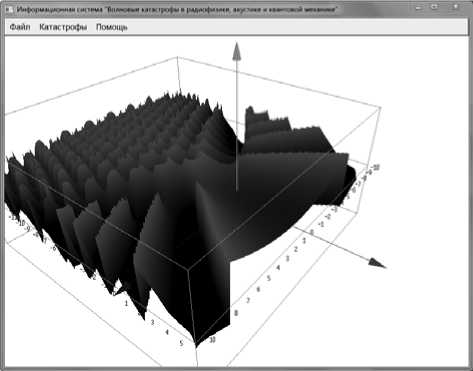
Рис. 2. Особенность А₃, фаза, λ ₁ = –15..15, λ ₂ = –10..10

ВЕСТНИК 2013 № 4

Вычисление СВК сводится к решению системы обыкновенных дифференциальных уравнений известным численным методом (см. [5; 6]).

Системы обыкновенных дифференциальных уравнений, описывающих ряд СВК, были получены вручную [1; 6], в то же время, процесс их вывода может быть автоматизирован с применением систем символьных вычислений.

В рамках разрабатываемого программного комплекса вычисления производятся оптимизированной реализацией метода Кутты – Мерсона (4 порядок точности, автоматическое изменение шага [7]). В библиотеке также представлены методы с меньшей точностью, но более высоким быстродействием (метод Рунге – Кутты, метод Эйлера).

Благодаря специальной иерархии классов СВК может быть описана путем наследования родительского класса “Problem”, который уже реализует общую функциональность, характерную для большинства катастроф. Единственный метод, который требуется определить, – метод “calculate”, выполняющий вычисления. Также определяется ряд функций, описывающих непосредственно системы дифференциальных уравнений.

Вычисление СВК выполняется параллельно за счет разделения задачи на подзадачи, покрывающие свое множество значений параметров. Также возможно вычисление СВК в простой распределенной среде. На данный момент опробована реализация с сетью из двух машин. Ведется работа над организацией сети с множеством вычислительных узлов, множеством потребителей и одним сервером, распределяющим нагрузку (рис. 3).

ВЕСТНИК 2013 № 4

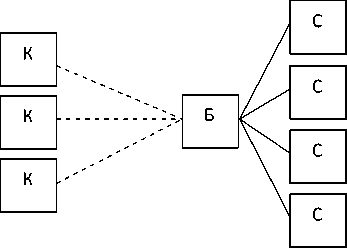
Рис. 3. Схема сети с тремя клиентами, балансировщиком нагрузки и четырьмя серверами

Грамматика предметно-ориентированного языка

С целью улучшения читаемости кода на рассматриваемом языке его грамматика основывается на подходах линии языков Никлауса Вирта [8], поскольку языки с подобной грамматической системой широко распространены в научной среде (Pascal, Modula, Oberon, в некоторой мере Ada, Algol). Тем не менее, грамматики названных языков слишком обширны и мало подходят в качестве модели встраиваемого специализированного языка программирования. С целью упрощения языка в грамматику явно не были включены такие конструкции, как циклы, ветвления, определения записей (структур), в языке отсутствует какая-либо развитая система типов. Программа на целевом языке имеет линейную структуру, не требует вызова каких-либо дополнительных процедур, что позволяет сосредоточиться на решении задачи, абстрактно описывая ее в терминах языка [9].

Описание грамматики языка включает примерно два десятка нетерминальных символов. Ключевые слова представлены как в кириллической, так и в латинской формах. Для ясности дальнейшего изложения разбирается лишь случай использования кириллических ключевых слов.

Программа, описывающая новую катастрофу, представляет собой модуль, состоящий из секций, каждая из которых есть отражение той или иной системы обыкновенных дифференциальных уравнений, записанных в виде, пригодном для численного решения.

Модуль начинается с ключевого слова «ОСОБЕННОСТЬ», за которым следует строка, описывающая данную катастрофу (обычно – буквенно-числовое обозначение особенности в соответствии с классификацией). Следующий семантический блок модуля – глобальные определения переменных и параметров: каждая переменная и параметр представлены в системе в виде чисел в формате, описываемом стандартом IEEE 754 [10]. Таким образом, нет необходимости вводить какие-либо конструкции, описывающие типы переменных. Список переменных начинается с ключевого слова «ПЕРЕМЕННЫЕ», список параметров – с ключевого слова «ПАРАМЕТРЫ». Важно заметить, что нетерминальные символы, представляющие объявления переменных и параметров для глобальной и локальной областей видимости, – различны. Данный факт связан с тем, что переменные могут иметь различную область видимости, в то время как параметры СВК едины для всей задачи. Ключевое слово «ВЕКТОРЫ» позволяет объявить ряд векторов, используемых в процессе решения. Данное ключевое слово может быть использовано как в глобальной области видимости, так и в локальных областях, образуемых описаниями отдельных систем.

Каждая секция, описывающая СОДУ, задается ключевым словом «СИСТЕМА», за которым следуют буквенно-числовой идентификатор и число уравнений в системе, заданное в круглых скобках. Как уже было замечено, внутри блока «СИСТЕМА» также возможны объявления переменных, тело блока помещается между ключевыми словами «НАЧАЛО» и «КОНЕЦ». Результирующий вектор, получаемый в результате одной итерации (решения системы для одного сочетания параметров), должен быть занесен в специальный вектор, определенный системой исполнения, имя которого «результат».

Основное тело программы следует за определениями систем уравнений, начинается ключевым словом «НАЧАЛО» и завершается ключевым словом «КОНЕЦ», за которым должна следовать точка. В основном теле программы позволяется инициализировать переменные и векторы, объявленные в глобальной области Грамматика языка записывается в расширен-видимости, а также вызывать подпрограммы ной форме Бэкуса – Наура [11] следующим об-библиотеки среды исполнения. разом:

Особенность = ОСОБЕННОСТЬ строка ; ГлобПослОбъявл { СИСТЕМА идент '(' число `)` ЛокПослОбъявл НАЧАЛО ПослОператоров КОНЕЦ} НАЧАЛО ПослОператоров КОНЕЦ `.`

ГлобПослОбъявл = ПАРАМЕТРЫ { СписокОпрПарам `;`} [ПЕРЕМЕННЫЕ { СписокИдент ';'}] [ВЕКТОРЫ { СписокОпрВект ';'}].

ЛокПослОбъявл = [ПЕРЕМЕННЫЕ { СписокОпрПерем `;`}] [ВЕКТОРЫ { СписокОпрВект ';'}].

СписокОпрПерем = ОпрПерем {',' ОпрПерем }.

ОпрПерем = идент ['<-' ПрефЧ исло | ИмпортЗнач].

ВЕСТНИК 2013 № 4

СписокОпрВект = ОпрВект {',' ОпрВект ]}.

ОпрВект = идент [ число ].

СписокОпрПарам = ОпрПарам {',' ОпрПарам }.

ОпрПарам = идент '(' ПрефЧисло | ИмпортЗнач , ПрефЧисло | ИмпортЗнач , ПрефЧисло | ИмпортЗнач ')' | идент '(' ПрефЧисло I ИмпортЗнач ')'.

ПрефЧисло = ['+' | '-'] число .

ИмпортЗнач = '$' число.

ПослОператоров = Оператор { Оператор }.

Оператор = Обозначение '<-' Выражение ';' .

ВЕСТНИК 2013 № 4

Слагаемое = Множитель { ОперУмнож Множитель }.
Множитель = Обозначение ['(' СписВыр ')'] |		число | '('	Выражение ')'.
СписВыр = Выражение {,	Выражение }.
Обозначение = идент [ '	[' Выражение ']' ].
Выражение = ['+' | '-'	] Слагаемое { ОперСлож	Слагаемое }.
ОперСлож = '+' | '-'.
ОперУмнож = '*' | '/'.
идент = буква { буква |	цифра }.
число = цифра { цифра }	'.' { цифра }.
строка = '’' { символ }	'’'.

Грамматика относится к классу LL(1). Текст программы, записанной с применением данной грамматики, может быть проанализирован с применением метода рекурсивного спуска или другим нисходящим методом. Семантический анализ и генерация кода могут быть выполнены за один проход, фактически исключая такую стадию трансляции, как построение дерева про

ОСОБЕННОСТЬ 'A3'

ПАРАМЕТРЫ lambdal ($1, $2, $3), lambda2 ($4,

граммы, поскольку в случае метода рекурсивного спуска данная структура данных образуется косвенным образом на стеке вызовов синтаксического анализатора.

Программа, вычисляющая СВК особенности A3, записывается в терминах данной грамматики следующим образом:

$5, $6);

ПЕРЕМЕННЫЕ gammal <- 3.625609908, gamma2 <- 1.225416702;

ВЕКТОРЫ

y[6];

СИСТЕМА A3 (6)

ПЕРЕМЕННЫЕ l1, l2, i21m, i21r, i22m, i22r; НАЧАЛО l1 <- lambda1 * t; l2 <- lambda2 * t;

i21r <- 0.25 * (l1 * y[1] + 2.0 * l2 * y[4]);

i21m <- 0.25 * (l1 * y[2] - 2.0 * l2 * y[3]);

i22r <- 0.25 * (y[2] + l1 * y[4] + 2.0 * l2 * y[6]);

i22m <- 0.25 * (-y[1] - l1 * y[3] - 2.0 * l2 * y[5]);

результат[1] <- lambda1 * y[3] + lambda2 *y[5]

результат[2] <- lambda1 * y[4] + lambda2 *y[6];

результат[3] <- -lambda1 * y[6] + lambda2 * i21r; результат[4] <- lambda1 * y[5] + lambda2 *i21m;

результат[5] <- lambda1 * i21r + lambda2 *i22r;

результат[6] <- lambda1 * i21m + lambda2 *i22m;

КОНЕЦ

НАЧАЛО

y[1] <- 0.5 * gamma1 * cos(PI / 8);

y[2] <- 0.5 * gamma1 * sin(PI / 8);

y[3] <- 0;

y[4] <- 0;

y[5] <- -0.5 * gamma2 * sin(3 * PI / 8);

y[6] <- 0.5 * gamma2 * cos(3 * PI / 8);

результат <- МетодКуттыМерсона(A3, КОНЕЦ .

Конструкции, начинающиеся со знака “$” в описании параметров СВК служат для связи программы со средой исполнения, а именно – для импорта значений, предоставляемых средой, например через графический интерфейс.

Процесс вычислений может быть распараллелен автоматически, поскольку в рамках описанной грамматики объявление параметров предшествует основному тексту программы, информация об их количестве и диапазонах значений позволяет заранее разделить задачу на подзадачи.

Среда исполнения

Код описанного предметно-ориентированного языка транслируется в переносимое промежуточное представление, являющееся кодом простой стековой виртуальной машины с фиксированной длиной команды.

Среда исполнения представляет собой совокупность виртуальной машины, способной ис- y);

полнять код промежуточного представления, и библиотеки окружения, включающей функции численного решения ОДУ, процедуры работы с потоками, примитивами синхронизации и сетью. Код библиотеки окружения написан с использованием языка программирования C++, что гарантирует его быстрое исполнение.

Среда исполнения автоматически создает необходимое число вычислительных контекстов, запускаемых в разных потоках на локальной или удаленных машинах. Таким образом, вычисления выполняются с привлечением всех доступных аппаратных ресурсов.

В процессе разработки виртуальной машины в дальнейшем планируется уделить внимание такому подходу, как JIT-компиляция. Поскольку входной язык не позволяет явно создавать конструкций ветвления или циклов, базовые блоки данного языка достаточно велики, что позволяет организовать эффективную компиляцию времени исполнения. В таком случае, сгенери-

ВЕСТНИК 2013 № 4

ВЕСТНИК 2013 № 4

рованный код не должен уступать в производительности коду, разработанному на каком-либо компилируемом языке программирования (например, C).

Выводы

Рассмотрен вопрос проектирования специализированной системы расчета СВК и предметно-ориентированного языка, применяемого в рамках системы для описания катастроф, подпрограммы вычисления которых не заложены в комплекс по умолчанию. Подход с применением специального предметно-ориентированного языка позволяет улучшить переносимость программного пакета, упростить его расширение, увеличить уровень абстракции и скрыть механизмы, связанные с параллелизмом и распределенной обработкой.

На данном этапе разработаны лексический и синтаксический анализаторы входного языка. Ведется работа над генератором кода и виртуальной машиной для последующего внедрения в программный комплекс.

В дальнейшем полученные в работе результаты планируется применить для развития открытой информационной системы «Волновые катастрофы в радиофизике, акустике и квантовой механике» [12–14].