Проектирование штампованной оснастки для способа отбортовки из конической заготовки эластичной средой

(в начальный момент) между матрицей и секторами. Для надежного обеспечения условия зажима эластичного элемента необходимо, чтобы его высота была больше высоты рабочей поверхности, но не превышала общую высоту матрицы, иначе эластичный элемент может попасть в зазор между матрицей и секторами. Это устраняет сжимающие силы трения на внутренней поверхности заготовки. Эластичный элемент в случае применения двух конических оболочек 3 и 4, деформируясь, увеличивается в диаметре и уменьшается в толщине, то есть соответствует условию плоского деформированного состояния, когда деформация по толщине ε _S равна по величине и противоположна по знаку деформации увеличения диаметра эластичного элемента

^ε θ . В этом случае приближенно можно записать условие постоянства объема (см. формулу 1):

ρ - r   S - S

ε _S ≈ - ε_θ или ≈ -      ⁰ ,    (1)

r S ₀

где ρ , r – соответственно радиусы по средней поверхности средние по высоте эластичного элемента до и после деформации;

S ₀ , S – соответственно толщины средние до и после деформации.

Несмотря на уменьшение толщины эластичного элемента в виде двух конических оболочек, прирост объема Δ V _ρ его за счет увеличения диаметра должен компенсировать разницу между внутренним объемом, ограниченным рабочей поверхностью матрицы и объемом, ограниченным наружной поверхностью эластичного элемента в виде двух конических оболочек в исходном состоянии Δ V (см. формулу 2).

A V _p = А V или п

Р² - r ² ) ’

cos а

h_M = А V , (2)

где h_м – высота рабочей поверхности матрицы;

α – угол конусности конуса.

Выразим r из (1) и, подставив его в (2) после преобразований получим:

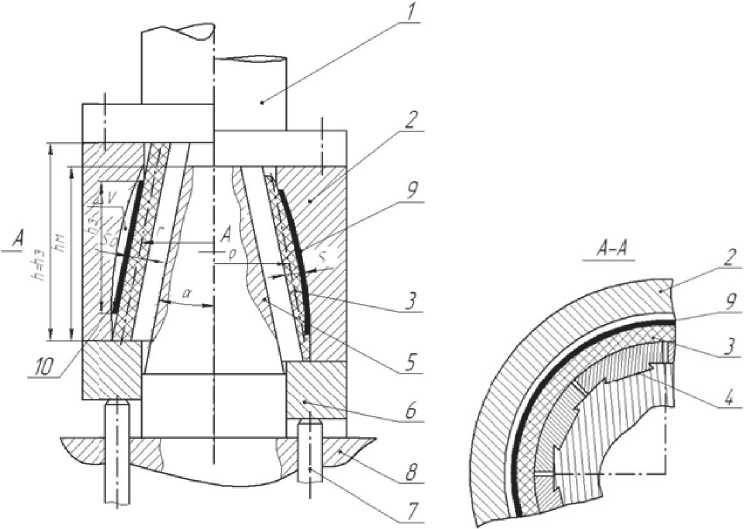
Рис. 1. Устройство для формообразования тонкостенных осесимметричных деталей усеченной сужающейся формы:

1 – пуансон; 2 – матрица; 3 – эластичный элемент; 4 – подвижные сектора; 5 – конус;

6 – опорное кольцо; 7 – шпилька; 8 – плита пресса; 9 – деталь; 10 – заготовка

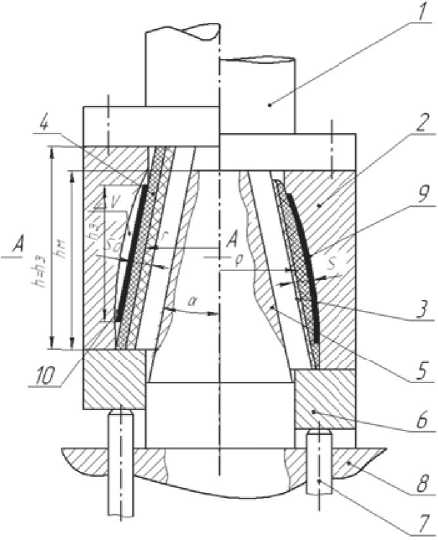
Рис. 2. Устройство для формообразования тонкостенных осесимметричных деталей усеченной сужающейся формы:

1 – пуансон; 2 – матрица; 3 – эластичный элемент; 4 – эластичный элемент; 5 – конус;

6 – опорное кольцо; 7 – шпилька; 8 – плита пресса; 9 – деталь; 10 – заготовка; 11 – подвижные сектора

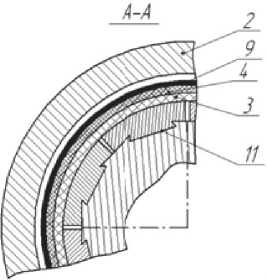
с < ^ Р = I 2-- 1    S о 7

А V cos a П- hM

"с      S ^ 2 [ 2 -у + 1 1    S 0 J

.(3)

S = 2

Р а

-

Приняв во внимание, что р = р _а - 0,5 S имеем:

-

S

S о

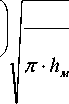
А V cos а

-

S

S о

+1

J 7

Исходную толщину эластичного элемента в виде двух конических оболочек найдем, поставив ограничения по степени деформации:

S

— <  k <  0,9 + 0,75 или

Sо        ,

^S = ^S 1 ^{+ S} 2 ; S о = S ll S l , _r„ k

S i + S 2 = 2 p_d - (2 - k )

I

A V cos a _ nh_M [ ( 2 - k ) ² + 1 ]

)

, (4)

где ρ _д – средний радиус детали;

S₁ – толщина внешнего эластичного элемента;

S₂ – толщина внутреннего эластичного элемента.

Улучшение современной авиационной техники, и в тоже время ее усложнение, повышение требований к качеству и надежности приводит к расширению производства технологической оснастки, проектирование и изготовление которой по трудоемкости составляет около 80 %, а по длительности – до 90 % общей трудоемкости и длительности технологической подготовки производства. Рассмотрим методику проектирования элементов оснастки для способа получения тонкостенной осесимметричной детали усеченной сужающейся формы.

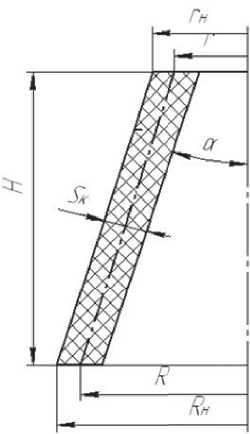
Рис. 3. Эластичная коническая оболочка: H – высота эластичного конического элемента;

R , R_н – больший радиус по срединной и наружной поверхности эластичного конического элемента; r , r_н – меньший радиус по срединной и наружной поверхности эластичного конического элемента; S_к – толщина эластичного конического элемента

. Расчет матрицы на прочность:

так как контейнер находится под внутренним давлением, то с целью безопасности эксперимента необходимо рассчитать его на прочность. Используя выводы расчета на прочность толстостенных цилиндров, нагруженных изнутри равномерным давлением [8], определили напряжения в тангенциальном направлении:

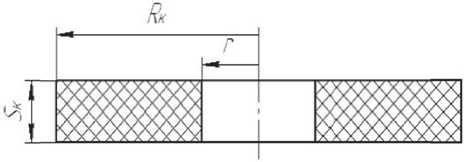
Рис. 4. Эластичный элемент в виде кольца: R_к – больший радиус кольца;

r – радиус отверстия в кольце; S_к – толщина кольца

Од = —

⁹ R

q 2 ^Г конт

■ конт

^^^^^^B

г ² конт

+

q 2 ^Г конт Ri

- конт

R

■ конт

^^^^^^B

г ² конт

Г ² конт

< [ ^ 9 ] , (5)

нического эластичного элемента, а наружный радиус равен:

R

к

где R_конт , r_конт – радиусы контейнера наружный и внутренний соответственно;

q₂ – избыточное давление матрицы через заготовку на эластичный элемент, [ q ₂ ] <  0,1 кг / мм ² ;

[ ^ 9 ] - предельное значение напряжения в тангенциальном направлении.

r 2 ₊ ( ^^Г > 1 , sin a

. Для процессов формообразования эластичным элементом конической формы (см. рис. 3) будем считать, что схема сжатия эластичного конического элемента в виде толстостенной оболочки эквивалентна сжатию эластичного элемента в виде кольца (см. рис. 4).

При этом примем, что толщина толстостенной конической оболочки равна толщине эластичного элемента в виде кольца, внутренний радиус кольца равен наименьшему радиусу ко-

где r « гн - Sк, т.к. гн > Sк .

Выражение получено из условия равенства площадей по срединной поверхности конической эластичной оболочки и эластичного кольца. Предлагаемая модель позволяет рассчитать размеры эластичного конического элемента в виде толстостенной оболочки, если его размеры R_к , r_н , H определены геометрией заготовки.

При применении способов необходимо определить толщину эластичного элемента кроме использования формулы (4) еще из дополнительных условий. Рассмотрим их.

. Обеспечение отсутствия заполнения эластичными элементами зазора Δ . Рассмотрим схему действия сил в области зазора между подвижными секторами (см. рис. 5).

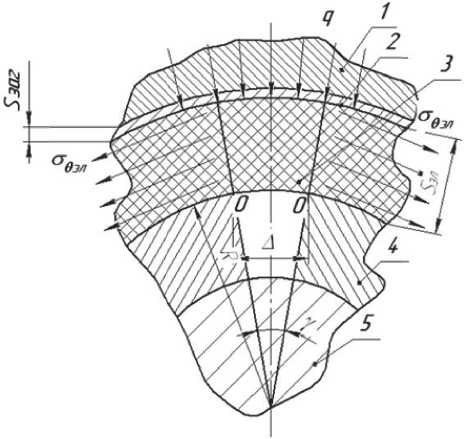
Рис. 5. Схема действия сил на эластичный элемент в области зазора между подвижными секторами:

1 – матрица; 2 – заготовка; 3 – эластичный элемент;

4 - подвижный сектор; 5 - конус; А - зазор между секторами; у - угол наклона; R - радиус до наружной поверхности секторов; S_эл – толщина эластичного элемента; S_заг – толщина заготовки;

О_9эл . - тангенциальное напряжение растяжения эластичного элемента;

q – суммарное давление на эластичный элемент

Суммарное давление эластичной среды равно (согласно принципу суперпозиции):

q = q i + q 2 + q 3 ,            (11)

где q ₁ – давление заготовки на эластичный элемент;

q 2 – избыточное давление матрицы через заготовку на эластичный элемент, [ q ₂ ] <  0,1 кг / мм ².

Составляющая сжатия от напряжения растяжения эластичного элемента:

Y q 3 = ^ 6 Эл Sin- ,

где у = arctg

А

2 R

заг

(см. рис. 5),

где R_заг – радиус цилиндрической заготовки. Из уравнения Лапласа [9]:

_ мзаг q1 = D   °63аг ,

R заг

где ^ е _заг - О _в - тангенциальное напряжение растяжения в заготовке.

С учётом выражений (8 ^ 13) равенство (7)

примет вид:

, (

О р эл . • S эл . ^ q 2

У

S заг R заг

• Y I А ²

О 9 + ^ б эл . srnj J у. (14)

Чтобы эластичный элемент не продавливался в зазор А , необходимо соблюдать равенство моментов от действия растягивающих и сжимающих сил относительно сечений перпендикулярных плоскости чертежа и проходящих через точки «0».

M_P = M_СЖ , (7) где M_P , M_СЖ – изгибающие моменты соответственно от растягивающих и сжимающих сил на единицу ширины.

В первом случае имеем:

М р = а _м . • -_эл . , (8)

где О9эл - напряжение растяжения в эластич- ном элементе.

Во втором случае:

_w _ а ^А

^Мсж = q • ^А • 2 ,

где А - зазор между подвижными секторами.

Величина зазора определяется из условия:

2nR 1 - 2 n r_o N

где N – число секторов;

R₁ – радиус по наружной поверхности подвижных секторов в момент окончания деформации в сечении, которое в исходном состоянии находилось в плоскости разъема матрицы с радиусом r₀ .

Отсюда имеем:

А2

[ Я 2 ⁺ ^ заг ^/ R заг " ^О 9 ^{+ О} 9 эл ' ®^1п ( / ^{/ 2} )]~

S эл . > ---------------------------------------- ^ . (15)

^О б эл .

Условие (15) гарантирует отсутствие затекания эластичного элемента в зазоры между подвижными секторами. В противном случае процесс проводить нежелательно. Ограничения зависят и от относительной толщины заготовки, и от давления эластичной среды, на которое влияет величина вытесненного объёма (форма и размеры детали).

. Расчет толщины конической эластичной оболочки определяется исходя из необходимого давления. Для этого используются диаграммы сжатия эластичного элемента (резины), которые достаточно широко представлены (см. рис. 6). Условием выбора толщины и относительных размеров эластичного в виде кольца служит максимальная величина сжатия по толщине не превышающая 10-15% , при выбранном значении q₂ (см. формулу 11).

Необходимо выполнить условие, чтобы величина сжатия резины не превышала в местах наибольшего деформирования более 30%.

Далее из рассчитанных толщин (см. формулу 4, 15 и см. рис. 6) выбирается наименьшая.

. Определение числа и размеров подвижных секторов. Схема для расчета представлена на рис. 7.

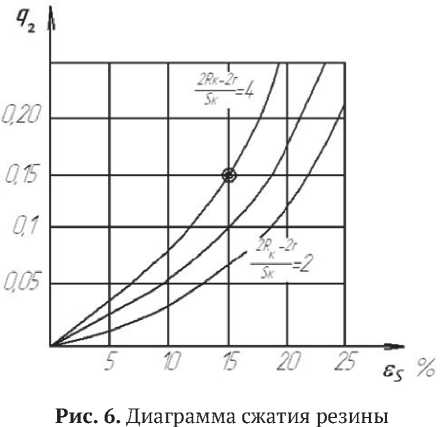
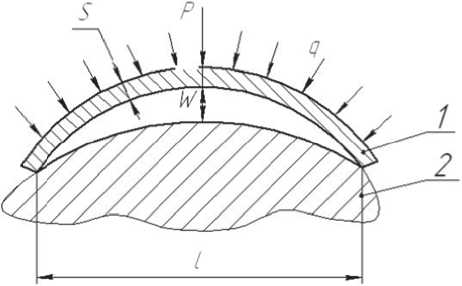
Рис. 7. Схема действия сил на подвижный сектор: P – результирующее усилие; q – давление эластичной среды;

1 – подвижный сектор; 2 – конус

Подвижные сектора 1 получены путем распила конической оболочки прилежащей к конусу 2,вдоль образующих на несколько частей. Поэтому при движении вдоль конуса отсечений меньшего диаметра к большему образуется зазор ϖ между внутренней поверхностью подвижного сектора 1 и поверхностью конуса 2.

Подвижный сектор должен передавать усилия от пресса при минимальной толщине, не деформируясь и не разрушаясь. Поэтому размеры сектора l, S должны быть согласованные с давлением среды q . Необходимым условием согласования этих параметров может быть равенство момента внутренних и внешних сил:

Ми = Мв ,(16)

где М_и , М_в – моменты внешних и внутренних сил.

Будем считать:

ми = P ■ l = q^-,(17)

"2

^ ²

M = ^0,2^-.(18)

Из условия (17; 18) имеем:

S

2 q ■ l ²

0,2

где l – ширина подвижного сектора в сечении наибольшего радиуса Rc. Его длина определяется:

, 2nRc l =-,

N

где N – число секторов.

Из равенств (19 и 20) можно определить:

N =

8 ⋅ q π ² R_c ²

^σ 0,2 ^{S 2}

. Рассчитываются усилия процессов формообразования эластичным буфером сложных деталей с подвижными секторами.

Схема к определению усилия представлена (см. рис. 8).

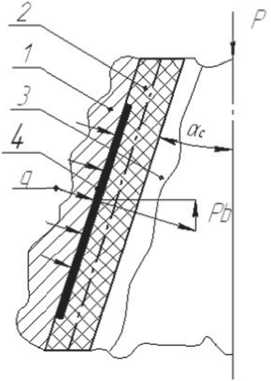
Рис. 8. Схема действия сил на подвижный сектор: 1 – матрица; 2 – эластичный элемент;

3 – подвижный сектор;

q – давление эластичной среды;

Рв – внутреннее усилие сопротивления;

Р – внешнее усилие; α _c – угол конусности

Запишем условие равенства внешнего и внутреннего усилия:

Р_в = Р ,                   (22)

где Р_в – результирующее внутреннее усилие.

P_e = K₃qF ■ sin a c .          (23)

При анализе назначения новых способов и оценке их технологичности важным является проработка методики проектирования элементов оснастки, так как это определяющая часть оснащения производства и оборудования с целью выполнения определенной задачи технологического процесса [10]. Обоснованная методика способствует повышению производительности; точности обработки, сборки и контроля; облегчению условий труда; сокращению количества и снижению квалификации рабочих; строгой регламентации длительности выполня- емых операций; расширению технологических возможностей оборудования; повышению безопасности рабочих и снижению аварийности.