Проектирование системы реконструкции и измерения расстояния на основе структурированного света и бинокулярного всенаправленного зрения

Всенаправленные системы зрения, обеспечивающие круговой обзор в 360°, получили широкое распространение в задачах моделирования окружающей среды, роботизированной навигации, локализации и слежения [1]. Типичная система состоит из выпуклого зеркала и стандартной камеры, что позволяет получать панорамное изображение за один съемочный цикл, устраняя необходимость сшивки кадров в многокамерных конфигурациях и тем самым значительно повышая эффективность сбора данных [2]. В последние годы камеры «рыбий глаз», обладающие низкой стоимостью, простой конструкцией, компактными размерами и широким углом обзора [3], нашли широкое применение в задачах внутренней реконструкции, интеллектуального транспорта и системах безопасности. Например, такие камеры способны эффективно воспринимать элементы архитектурной среды – пол, стены и потолок – для обеспечения 3D-реконструкции помещений [4], обеспечивать обзор до 180° при высокоточной детекции транспортных средств и пешеходов в системах дорожного мониторинга [5], а также устранять слепые зоны в системах бытового видеонаблюдения благодаря сверхширокому углу обзора [6].

Несмотря на перечисленные преимущества, камеры «рыбий глаз» сталкиваются с рядом существенных технических вызовов. Главным из них является выраженная радиальная дисторсия, устранение которой традиционными методами приводит к уменьшению эффективного поля зрения и появлению артефактов пересэмплирования на краях изображения [7]. Дисторсия также вызывает смещение объектов, что снижает точность локализации и планирования траектории в навигационных системах и в ряде случаев приводит к ошибкам обнаружения препятствий [8]. Кроме того, изменения освещения, шумы и сложный фон дополнительно снижают робастность визуальной системы. Для повышения точности измерений структурированный свет [9] постепенно становится одним из ключевых вспомогательных методов.

В зависимости от типа используемого источника излучения системы компьютерного зрения подразделяются на активные и пассивные [10]. Пассивные системы зрения [11], опирающиеся на естественное освещение, подвержены трудностям сопоставления признаков и ошибкам оценки глубины в малотекстурированных средах (например, под водой) и сильно зависят от условий освещения. Активные системы зрения [12], посылающие в сцену структурированное излучение, способны эффективно преодолевать перечисленные ограничения, что обусловило их широкое исследование. Например, Т. Wu и др. применили отслеживание лазерной полосы для анализа вибраций мостовых конструкций [13]; Z. Tan и др. интегрировали поляризационную камеру с линейным структурированным светом для 3D-реконструкции сварных швов, устранив влияние дугового излучения [14]. Таким образом, визуальные системы, объединяющие всенаправленное изображение и структурированный свет, привлекают значительное внимание благодаря широкому охвату сцены и высокой эффективности измерений.

На этом фоне в данной работе предлагается алгоритм реконструкции контуров препятствий, основанный на совместном использовании двух панорамных камер и структурированного света. Метод не требует предварительного обучения на выборках или явного сопоставления признаков; вместо этого осуществляется прямая интеграция изображений двух камер, позволяющая одновременно выполнять реконструкцию формы и оценку расстояния при сниженных вычислительных затратах. По сравнению с традиционными методами всенаправленной реконструкции предложенный алгоритм предъявляет менее строгие требования к размещению камер и сохраняет высокую точность реконструкции даже в условиях низкой текстурно-сти и малого параллакса.

Метод реконструкции

Метод измерения расстояния на основе структурированного света во всенаправленной системе зрения позволяет быстро вычислять расстояние

между препятствием и центром системы наблюдения. Для этого фиксируется структурированный свет, проецируемый на поверхность объекта, а затем выполняется преобразование по уравнению плоскостной проекции. Соответствующее уравнение преобразования проекции имеет следующий вид:

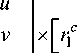
ccll r2    r3  II r1    ri

. f ( p )

X

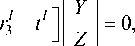
где u , v обозначают координаты пикселя изображения; / jc , / 2 , r c - векторы матрицы вращения камеры; параметры l 1 , l 2 , l 3 являются векторами матрицы преобразования плоскости лазерного луча; а X , Y , Z – пространственные координаты точки лазерной проекции.

В выражении (1) функция f ( p ) может быть представлена следующим образом:

^{f (} Р ) = а о + a 2 P²+- + a n P n ;

p — (uu - uc )2 + (v - vc )2, где ai – коэффициенты полинома, N – его степень, а uc и vc обозначают координаты центра всенаправленного изображения.

Поскольку расстояние между лазерной плоскостью и оптическим центром камеры является постоянным и заранее известным, координата Z реконструируемых данных во всенаправленной системе остается неизменной. Следовательно, в уравнении (1) можно принять Z = 0, и оно преобразуется к виду

u

v f (P)

x [ / j c

cc r2   r3

В векторе t^l первые два элемента соответствуют расстоянию между плоскостью структурированного света и началом координат камеры. В задаче двумерного отображения структурированного света лазерная плоскость фиксирована и не изменяется в ходе реконструкции; поэтому, если расстояние до плоскости и параметры положения камеры известны, уравнение может быть упрощено до следующего вида:

u

v

.^{f (} P )

X x [hj   h   h3 ] Y = о.

После дальнейшего упрощения выражения (5) оно может быть представлено следующим образом: v (h3i X + h32 Y + h33) - f (P)(h2i X + h22 Y + h23) = 0;(6)

f (p)( hj j X + hj2 Y + hj3) - u (h3i X + h32Y + h33) = 0;(7)

u (h21 X+h22Y+h23) - v (h11 X+h12 Y+h13) = 0.(8)

В итоге, объединяя приведённые выше выражения, можно получить пространственные координаты реконструированной точки структурированного света в системе координат камеры:

X = ( - c - b 1 Y )/ a p

Y =(a2с - a c2) /(a b2 - a2b1), где a1 = f (ρ)h11 - uh31, b1 = f (ρ)h12 - uh32, c1 = f (ρ)h13 - uh33, a2 = uh21 - vh11, b2 = uh22 - vh12 и c2 = uh23 - vh13.

Результаты преобразования всенаправленного изображения по указанным уравнениям представлены на рис. 1. Предложенный метод эффективно устраняет искажения, возникающие во всенаправленной оптике, и обеспечивает корректную реконструкцию структурированного света.

Для унификации реконструируемых данных нескольких камер мы, основываясь на принципах построения роботоориентированных систем координат, ввели пространственную систему координат, независимую от обеих систем зрения, совпадающую с началом базовой системы робота. В этой системе координат достаточно знать положение и ориентацию каждой камеры, чтобы преобразовать и объединить их независимые результаты реконструкции в единое представление. Угол поворота между пространственной системой координат и системой камеры обозначим как 0 . Тогда матрица координат структурированного света после вращательного преобразования имеет вид

M = R„ • [ X ; Y ;1 ] , (10)

где R_cv – матрица вращения, задающая ориентацию системы координат камеры в пространственной системе, а X и Y – координаты структурированного света, полученные в уравнении (9). Матрица вращения R_cv имеет следующий вид:

	cos( 0 )	- sin( 0 )	0
R cv =	sin( 0 )	cos( 0 )	0
	_    0	0	1

После выполнения коррекции на основе вращения координат необходимо произвести окончательное преобразование с учётом положения оптического центра камеры в пространственной системе координат. Соответствующее уравнение имеет вид

x

y

= M +

xcv ycv

где x_cv и y_cv – координаты камеры «рыбий глаз» в унифицированной системе координат, а x и y – координаты структурированного света в той же системе.

В результате указанных преобразований данные структурированного света, независимо реконструированные двумя камерами, преобразуются в единую систему координат. Процесс преобразова-

ния показан на рис. 2. Наложив преобразованные данные реконструкции, можно получить более полное представление формы препятствия. На основе существующей функции измерения расстояния использование нескольких камер позволяет более точно восстановить внешний контур объекта и расширить область воспринимаемой структуры окружающей среды.

Экспериментальные результаты и анализ

Для оценки работоспособности разработанной системы «виртуальной реальности» и предложенного метода реконструкции данных бинокулярного всенаправленного зрения были проведены всесторонние испытания, включающие: оценку качества реконструкции объектов в виртуальной среде и проверку точности измерения расстояния до препятствий в реальных условиях. Виртуальная симуляционная система функционировала на платформе Windows, при этом использовался процессор AMD Ryzen 5 5600U CPU @ 2.30 GHz

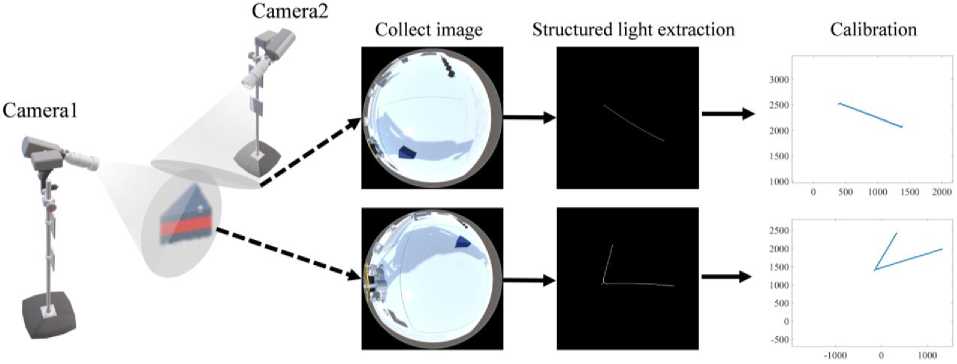
Рис. 1. Результаты измерения расстояния до препятствий в различных всенаправленных системах зрения Fig. 1. Obstacle distance measurement results under different omnidirectional vision systems

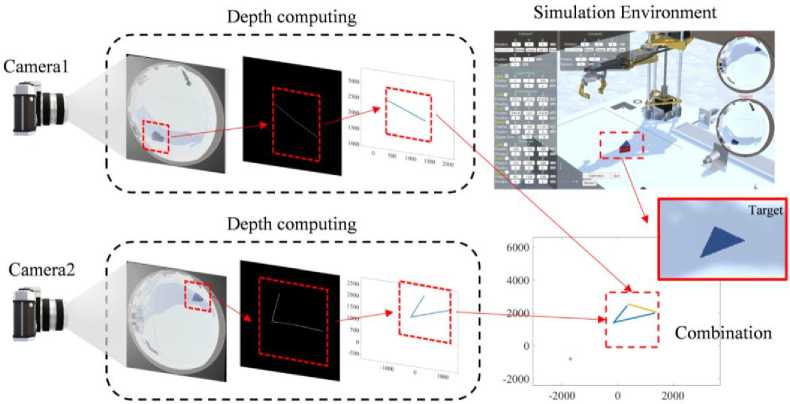
Рис. 2. Схема объединения данных в бинокулярной всенаправленной системе зрения

Fig. 2. Data integration workflow of the binocular omnidirectional vision system

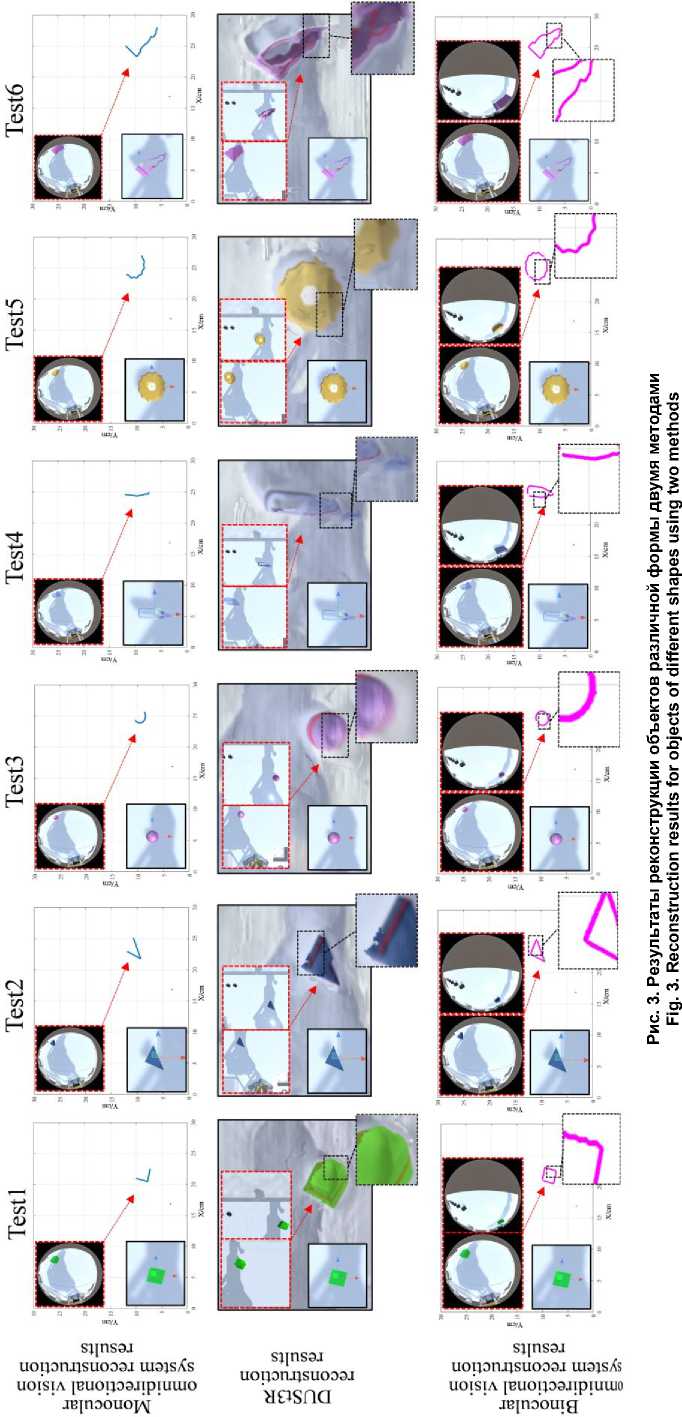
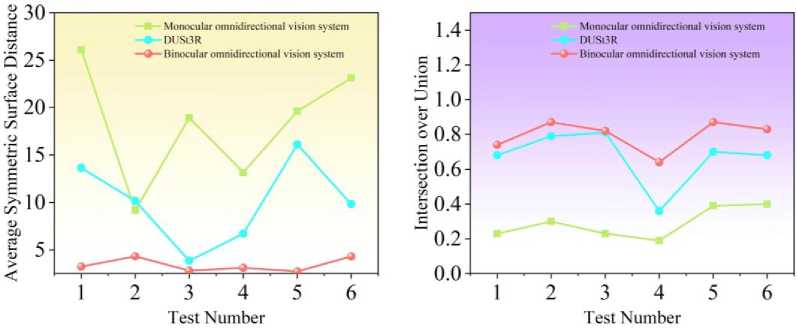
Рис. 4. Сравнение точности реконструкции объектов различной формы разными методами Fig. 4. Comparison of reconstruction accuracy for objects of different shapes using different methods

с 6 ядрами и 16 ГБ оперативной памяти. В реальных экспериментах была использована аппаратная платформа, состоящая из линейного лазерного генератора с длиной волны 650 нм и промышленной камеры «рыбий глаз» HF890,

Результаты реконструкции объектов

По сравнению с традиционными системами зрения всенаправленные системы обеспечивают более широкий угол обзора, что позволяет фиксировать значительно больший объём информации об окружающей среде. Однако при регистрации объекта одна всенаправленная камера зачастую не может получить полную информацию о форме объекта: из-за ограничений ракурса часть структурированного света на многогранных телах остаётся недоступной, что приводит к неполной реконструкции внешнего контура. В бинокулярной всенаправленной системе, напротив, многократные углы наблюдения позволяют получить более полное структурированное изображение объекта. Для оценки качества реконструкции различных объектов в виртуальной тестовой среде были выбраны шесть моделей, включающих три объекта регулярной геометрической формы и три объекта со сложной криволинейной поверхностью. Указанные модели были реконструированы с использованием монокулярной системы зрения, алгоритма DUSt3R и бинокулярной панорамной системы, после чего результаты были сопоставлены. Экспериментальные результаты представлены на рис. 3. Как видно, монокулярная панорамная система фиксирует ограниченный объём данных структурированного света, вследствие чего объект восста- навливается лишь частично. Для объектов регулярной геометрии алгоритм DUSt3R демонстрирует высокое качество восстановления: реконструированные контуры хорошо совпадают с исходной моделью. Однако при реконструкции объектов со сложной криволинейной поверхностью качество заметно снижается. В тесте 4 нижняя часть модели пинцета оказалась частично скрыта фоном; в тесте 5 зубчатая область модели шестерни была реконструирована с выраженной нечеткостью. В отличие от них, бинокулярная панорамная система успешно регистрирует данные структурированного света как для регулярных, так и для нерегулярных объектов и обеспечивает их последующее объединение, что позволяет выполнять полноценную реконструкцию формы. Даже при восстановлении сложных объектов в итоговых данных отсутствуют заметные пропуски или потеря информации.

Для более точной оценки качества реконструкции формы объектов в двух методах были использованы два показателя: среднее симметричное расстояние (ASD) и коэффициент пересечения-объединения (IoU). Показатель ASD вычисляет среднее минимальное расстояние между всеми точками двух контуров и служит для оценки степени их взаимного соответствия: чем меньше значение ASD, тем выше качество реконструкции. Коэффициент IoU определяется как отношение площади пересечения реконструированной и реальной областей к площади их объединения; значение лежит в диапазоне 0–1, и чем ближе оно к 1, тем точнее восстановленная форма. На рис. 4 представлены значения ASD и IoU для всех шести тестовых сцен, полученные различными методами.

Параметры установки реальной камеры «рыбий глаз» Installation parameters of the real fisheye camera

Система	Параметры камеры					Расстояние между камерой и плоскостью структурированного света, мм
	x , мм	y , мм	Тангаж, °	Крен, °	Рыскание, °
Камера 1	140	194	1	3	1	131
Камера 2	–122	100	4	2	2	131

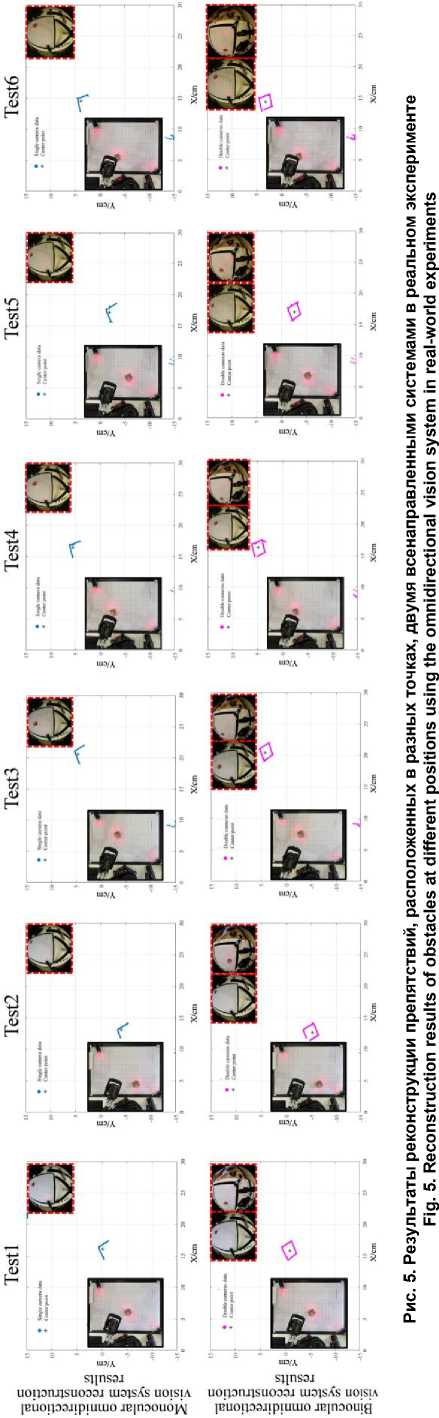
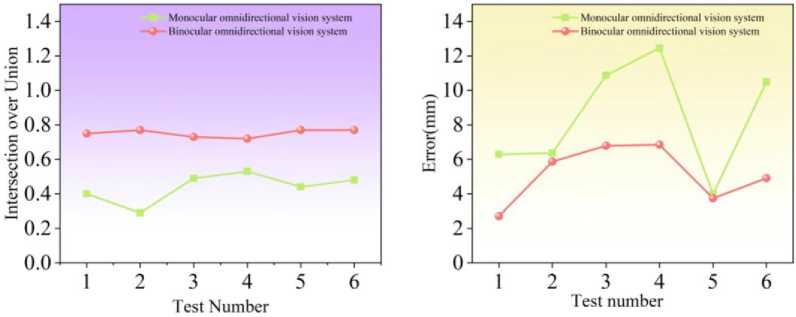
Рис. 6. Сравнение результатов двух всенаправленных систем в реальной среде: слева – точность реконструкции, справа – точность локализации

Fig. 6. Comparison of test results for two omnidirectional vision systems in real-world environments: reconstruction accuracy (left) and localization accuracy (right)

Во всех экспериментах многовидовая система стабильно превосходит как монокулярную систему, так и DUSt3R. При реконструкции объектов различных форм среднее значение ASD для монокулярной системы составило 18,34, для DUSt3R – 10,06, тогда как многовидовая система достигла значительно меньшего значения – 3,42, что свидетельствует о более высокой точности согласования контуров и меньшей ошибке реконструкции. Аналогичным образом, по показателю IoU монокулярная система в среднем дала значение 0,29, DUSt3R – 0,67, причём при сложной геометрии точность заметно снижалась; в то время как бинокулярная система достигла среднего IoU = 0,80, демонстрируя лучшую согласованность глобального контура и меньший пограничный сдвиг. Кроме того, при реконструкции объектов сложной и неоднородной геометрии бинокулярная система проявила высокую стабильность, сохраняя точность на устойчиво высоком уровне для всех типов объектов.

Результаты экспериментов в реальных условиях

В предыдущих экспериментах были сравнены результаты реконструкции, полученные различными методами, в виртуальной среде. Для оценки их практической применимости была создана реальная бинокулярная панорамная система зрения, конфигурация которой соответствовала параметрам виртуальной платформы. В системе использовался красный лазерный излучатель в качестве источника структурированного света, а тестовым объектом являлся куб с длиной ребра 1 см. Куб случайным образом размещался в различных точках тестовой площадки, после чего с помощью бинокулярной панорамной системы выполнялась двумерная реконструкция и оценка координат. Положение куба определялось как среднее значение координат точек реконструированно- го контура. Было проведено шесть экспериментальных измерений. Поскольку алгоритм DUSt3R демонстрирует низкую точность глубинной оценки на малых расстояниях, в качестве базовой системы сравнения использовалась только монокулярная панорамная система. Параметры установки камеры «рыбий глаз», использованной в реальных экспериментах, приведены в таблице. Эти параметры были получены с использованием метода калибровки, предложенного I. Kholodilin и соавт. [4].

На рис. 5 представлены результаты реконструкции куба двумя системами в реальном эксперименте. Как и в виртуальном эксперименте, из-за ограниченного угла обзора монокулярной всенаправленной камеры реконструкция куба оказалась неполной. В данном эксперименте камера 1 регистрировала структурированный свет только от верхней части куба, вследствие чего вычисленное значение координаты y существенно превышало действительное. Напротив, в бинокулярной системе координаты x и y были определены без заметных отклонений.

На рис. 6 приведено сравнение точности реконструкции и ошибок локализации целевой точки для двух всенаправленных систем в реальном тестировании. При реконструкции объектов, расположенных в различных позициях, бинокулярная система показала значительно более высокий средний показатель IoU – 0,502, что близко к результатам виртуального моделирования. Во всех шести тестовых сценариях ошибка определения положения точки в бинокулярной системе была ниже, чем в монокулярной. Средняя погрешность уменьшилась на 38,93 %. Таким образом, в реальных условиях разработанная бинокулярная всенаправленная система обеспечивает существенное повышение точности реконструкции и измерения, демонстрируя результаты, сопоставимые с виртуальным моделированием.

Заключение

В данной работе предложен метод реконструкции формы препятствий и измерения расстояний, основанный на интеграции бинокулярного всенаправленного зрения и структурированного света. Он позволяет по двум всенаправленным изображениям выполнять высокоточное восстановление трёхмерного контура сложных объектов и их пространственную локализацию. Предлагаемая система имеет простую аппаратную конфигурацию и требует только бинокулярной всенаправленной камеры и одного лазерного излучателя структурированного света. Кроме того, она допускает гибкую настройку положения и ориентации камер под конкретные задачи, устраняя необходимость в сложных и строгих процедурах установки и калибровки. Для проверки точности и робастности метода была проведена серия экспериментов. Результаты показали, что предложенный подход значительно превосходит монокулярную систему по качеству реконструкции формы и точности измерений, сохраняя стабильность при различных схемах установки камер. В экспериментах, выполненных в реальных условиях, система успешно реконструировала объекты, расположенные в различных точках, и корректно определила их центральные координаты, что дополнительно подтверждает практическую эффективность и прикладную ценность разработанного метода.