Проектирование трехзначных цифровых нейронов

Одним из перспективных цифровых нейронов является нейрон сотовой структуры [1], функция возбуждения ^{ϕ ( X )} которого имеет вид:

i

1, если

Z w i x i = P j

0, в противном случае,

P где j — квазипорог нейрона, множество квазипорогов

{ P j }

w эмулирует порог ^P , ⁱ — вес

синапса ⁱ

Сумма весов

Z w

i

определяет сложность нейрона ^{L ( ϕ )}

L ( V ) = Z wi

i площадь “кремния”, реализующего его. В настоящее время цифровые нейроны промышленного назначения в России и США являются 4-синапситескими.

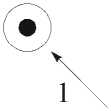
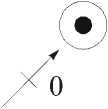
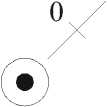
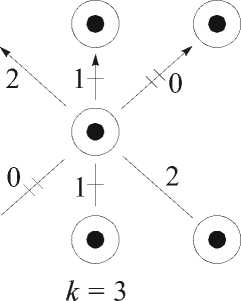
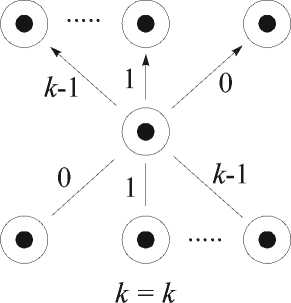
Обобщая структуру двузначного сотового нейрона (рис. 1, а), проф. А.В. Горбатов предложил [2] структуру k -значного однородного нейрона, локальная топология которого представлена на рис. 1 в. На этом рисунке неперечёркнутая дуга соответствует ключу, инициируемому при x = k – 1, остальные дуги соответствуют ключам, включаемым при x = k

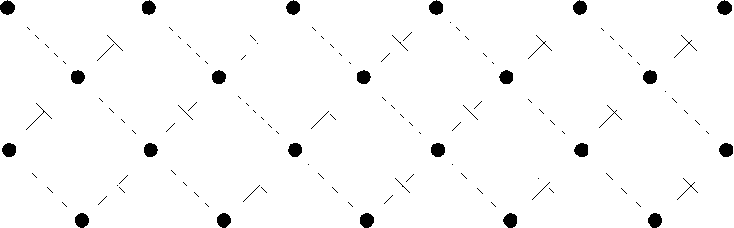
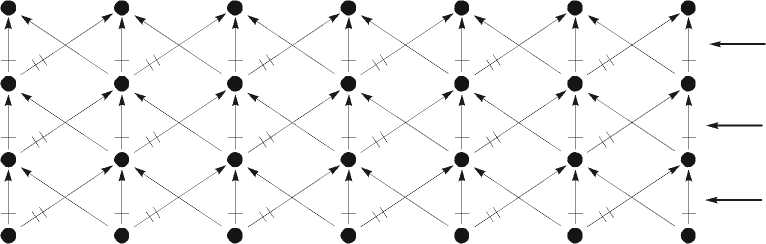
- 1 - а, где a — количество перечёркиваний дуги. Используя предложенную структуру однородных нейронов (рис. 1 а, б), на рис. 2 а, б представлены структуры однородных двузначного и трёхзначного нейронов соответственно.

Математическим описанием предлагаемых однородных к-значных нейронов является выражение (3):

s ф j (X1, x 2,K, Xs ) =

1, если V wx = T ii k i=1

0 в противном случае,

где   ф j  —  функция  возбуждения   j -ой  фазы  выходного  синапса  нейрона:

фj = 1 О ф = j, j G {0,1, K, к — 1}, w — вес i-го синапса, T — квазипорог нейрона, находящегося в j-м состоянии; множество квазипорогов {Tk } моделируют порог при возбуждении нейрона в j-м состоянии.

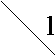
а)

в)

Рис. 1. Обобщая структуру двузначного сотового нейрона аксон

синапсы

x ₁

x ₂

x

порог

а)

x 1

x 3

б)

Рис. 2. Структуры однородных двузначного и трёхзначного нейронов

В статье предложена стратегия эффективной настройки k-значного сотового нейрона, исключающая трудоёмкую процедуру целочисленного решения “k” взаимосвязанных систем. Стратегия основана на орбитально непротиворечивое вложение заданной функции в k-значный гиперкуб.

Определение 1.

Орбитой относительно центра ^XC в k-значном пространстве называется множество

{X,}                         X

C

точек    ⁱ , равноудалённых от центра

{ X. 'X i /R ( X , X. ) = const }

,

R (X r- X.)                X.                      Xc где C i  - радиус точки i относительно центра C , равный минимальному

XX расстоянию между точками ⁱ и ^C

.

_n                    R ( X_c,X_t )

Очевидно, что радиус      ^{C i} равен сумме модулей разностей между значениями

X_C = ( X, ., X, ₇, K , X, „)    X, = ( X, ., X, ₇, K , x_in )

соответствующих разрядов векторов ^{C C 1 C 2       Cn} и ^{i     i 1 i 2 in} :

n

R ( X c , X^ U X cj - X j|

j = 1

Определение 2.

Распределение по орбитам относительно центра XC значений реализуемой k-значной функции называется непротиворечивым, если на каждой орбите не найдётся хотя бы двух точек, в которых эта функция принимает различные значения, при этом функция называется “непротиворечивой”, относительно центра XC или орбитально непротиворечивой.

Утверждение 1.

Вес каждого синапса k-значного сотового нейрона равен “1”, если найдётся непротиворечивое распределение по орбитам относительно центра XC значений реализуемой k-значной функции f(X) (орбитально непротиворечивого вложения функции в k-значный гиперкуб).

Стратегия эффективной настройки k-значного сотового нейрона при реализации произвольной k-значной функции f ^{( X 1, x 2, K , x} n ) сводится к построению орбитально непротиворечивой k-значной функции f ^{( X 1, x 2, K ,} x n + ^А n ) , эквивалентирующей заданную функцию.

Рассмотрим предлагаемую стратегию на примере.

Пусть задана 3-значная функция f (x, x2, x)

1 2 3 вида:

0 на 2,3,7,11,20, f (x1, x 2, x 3 ) = < 1 на 1,9,17,25,

2 на 4, 15, 21.

3-значный 3-местный гиперкуб имеет 7 орбит: 0-й орбите соответствует точка 0, 1-й орбите - точки 1, 4, 9; …; 6-й орбите точка 26. Распределение значений заданной функции по орбитам относительно центра 0 представлено на рис. 3, при этом номер орбиты равен сумме цифр вектора, определяющего точку этой орбиты.

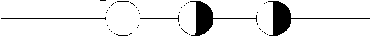
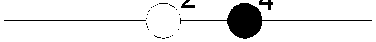
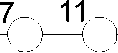
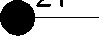
1-я орбита

2-я орбита

3-я орбита

4-я орбита

5-я орбита

Рис. 3. Распределение значений функции по орбитам относительно центра

Для оценки распределения значений функции введём отношение противоречивости

XX

R2 : две точки  ia , ib одной и той же i-ой орбиты находятся в отношении R2 , если и только если      ia ib 2            ia           ib .

P

Каждое распределение ^α значений функции будем оценивать L суммой сигнатур

G графов противоречивости ^{пр i}

, определяемых отношением ^{R 2} :

L (Pa ) =

( k - 1) - n

£ и

i = 0

Первое распределение P1 (см. рис.3) оценивается числом 7: 2+1+4=7 (рис.4).

3     2     7     11

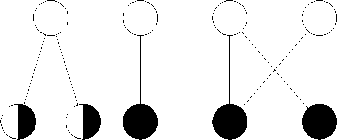
9    1   4     15    21

Рис. 4. Первое распределение заданной функции

G противоречивости     ^пр

Очевидно, что каждая компонента связности графа взаимнооднозначно соответствует определённому номеру орбиты.

Последовательно производим расщепление переменных, определяем соответствующее распределение значений, производим согласно (6) их оценку и выбираем расщепление переменной которому соответствует минимальное значение (6).

Расщепляем переменную ^{x 1} ,

Х ₁ ^ x ‘ , x ‘ .

'0 на 0002,0010,0021,1102,2202, f (x’, x1, x 2, x3) = Ь на 0001,1100,1122,2221,

2 на 0011, 1120, 2210.

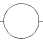
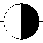
1-я орбита

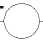
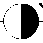
2-я орбита

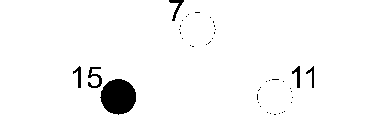
3-я орбита

4-я орбита

20             17

5-я орбита

6-я орбита

7-я орбита

Рис. 5. Второе распределение заданной функции

Оценка второго распределения (рис.5) - L ⁽ P 2 ) =1+з+1+1=6 (рис. 6).

3        2        11    20

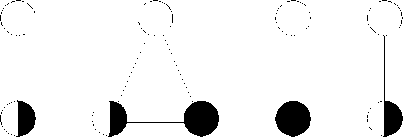
1     9     4     15    17

Рис. 6. Оценка второго распределения заданной функции

Расщепляем переменную x2 , x 2 ^ x ', x 2

'0 на 0002,0110,0221,1002,2002, f (x1, x 2

x 2' , x 3 ) = И на 0001,1000,1222,2221,

2 на 0111, 1220, 2110.

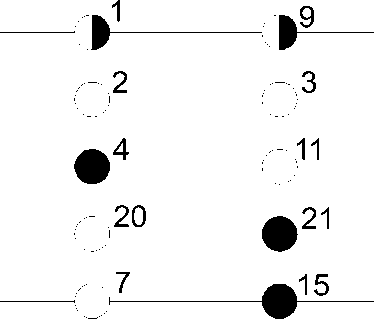
Оценка третьего распределения (рис. 7) -    3 =1+1+1=3 (рис. 8).

Расщепляем переменную ^{x 3}

x 3 ^ x ' , x "

'0 на 0022,0100,0211,1022,2022, f (x1, x 2, x', x3') = <

1 на 0011, 1000, 1222, 2211,

2 на 0111, 1200, 2100.

1-я орбита

2-я орбита

3-я орбита

4-я орбита

5-я орбита

6-я орбита

17          25

7-я орбита

Рис. 7. Третье распределение заданной функции

11     20     7

4     21     15

Рис. 8. Оценка третьего распределения заданной функции

1-я орбита

1            2-я орбита

21^ -

3-я орбита

4-я орбита

5-я орбита

20         25

6-я орбита

7-я орбита

Рис. 9. Четвертое распределение заданной функции

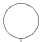
Оценка четвёртого распределения (рис. 9) -

L ( P 4 ) =1+1=2 (рис. 10).

>

э

Рис. 10. Оценка четвертого распределения заданной функции

1-е противоречие:

{ 3,9 } е R 2

2-е противоречие:

{ 20,25 } е R ₂

Для устранения выявленных противоречий кроме x ³ расщепляем ещё x ² (рис. 11).

Электронное научное издание «Устойчивое инновационное развитие: проектирование и управление»

том 6 № 1 (6), 2010, ст. 2

3-01100

9-10000

1-я

орбита

1-00011

2-я

орбита

3-я

2-02200    4-01111 21-21100

4-я

орбита

орбита

11-10022

15-12200

5-я

орбита

7-02211

20-22200

6-я

орбита

7-я

орбита

25-22211

8-я

орбита

17-12222

9-я

орбита

Рис. 11. Расщепление переменных Х 2 , Х 3

Оценка пятого расщепления (рис. 11)

L ^{( P} ) >  L ( P ) .

.

-

L (P ) A

5 =4, получили повышение оценки:

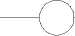
Для уменьшения оценок L ( P , ) и ^{L ( P} 5 ) очевидно, что необходимо расщепить ^{x 3} не на две, а на три переменные: ^{x 3} ^ ^x 3 ,^x 3 ,^{x 3} , при этом получаем орбитально непротиворечивое распределение значений исходной функции f ^{( x} 1 , ^x 2 ,^{x 3} ) (рис. 12).

функция

является

Оценка 6-го распределения (рис. 12) равна 0. Следовательно, f (x, x‘, x‘, x‘, x‘, xT)                                                             f (x, x7, x)

1 2 2 3 3 3 , эквивалентирующая заданную функцию      1 2 3 , орбитально непротиворечивой.

Отсюда веса синапсов x ¹ , ^{x 2} , ^{x 3} соответственно равны w ⁽ x ¹ ) ¹ , ^{w ( x 2} ) ² ,

.

Для определения квазипорогов для каждой фазы, строим соответствующие системы уравнений, при этом модель нейрона имеет вид (7):

У w x = T j

i

,

где ^wi – вес i-го синапса xi, Tkj – j-й квазипорог k-й фазы нейрона.

9-100000

1-я орбита

3-011000 о -

2-я орбита

1-000111

3-я орбита

21-211000

4-я орбита

4-011111          15-122000

5-я орбита

2-000222

11-100222

7-022111

6-я орбита

7-я орбита

20-200222

8-я

орбита

25-222111

9-я орбита

10-я орбита

17-122222 11-я орбита

Рис. 12. Оценка шестого распределения заданной функции

Система 0-й фазы:

' 2 ^ 002	2 • w3 = T 01 ^ 2 • 3 = 6,
3 ^ 010	W 2 = T 02 ^ 2,
7 ^ 021	2 • w 2 + w 3 = T 03 ^ 2 • 2 + 3 = 7,
11 ^ 102	w 1 + 2 • w 3 = T 04 ^ 1 + 2 • 3 = 7,
20 ^ 202	2 • w 1 + 2 • w 3 = T 05 ^ 2 • 1 + 2 • 3 = 8

T = { 2,6,7,8 }

Множество квазипорогов 0-й фазы:

Системы 1-й фазы:

' 1 ^ 001	w 3 = T 11 ^ 3,
9 ^ 100	W 1 = T 12 ^ 1,
17 ^ 122	w 1 + 2 • w 2 + 2 • w 3 = T ^ 1 + 2 • 2 + 2 • 3 = 11,
25 ^ 221	2 • w 1 + 2 • w 2 + w 3 = T 14 ^ 2 • 1 + 2 • 2 + 1 • 3 = 9.

Множество квазипорогов 1-й фазы: T 1 ^{{ 1,3,9,11 }}

.

Система 2-й фазы:

4 —011

< 15 — 120

21 — 210

w 2 + W 3 — T 21 —— 2 + 3 — 5, w + 2 • w ₂ — T 22 — 1 - 1 + 2 • 2 — 5, 2 • w 1 + w ₂ — T ₂₃ — 2 • 1 + 1 • 2 — 4.

Множество квазипорогов 2-й фазы:

T 2 — { 4,5 }

.

Условие ^(v T • T ^I T ^—0) , где «*j, «М0А К k - 1 } заданной функции на k-значном однородном сотовом нейроне.

определяет реализуемость

Сложность нейрона, равная сумме весов синапсов,

во многом определяется

X выбранным орбитальным центром ^C

.

Предложим   процедуру вычисления   оптимального

орбитального   центра,

проиллюстрировав её на следующем примере.

Определить настройку 3-значного сотового нейрона, f ⁽ x i , ^x 2 , ^{x 3} ) , равную с учётом оптимального орбитального центра ' 0 на 2,3,7,11, f ( Х 1 , x 2 , x 3 ) —< 1 на 1,19,24, 2 на 0,25,

реализующего функцию

X C

При произвольном орбитальном центра ^XC , модель k-значного сотового нейрона определяется выражением (8):

n

X W I x ci - x d\ ^{— P}pa

,

i — 1

где ^wi — вес i-го синапса, ^xci — значение i-го орбитального центра ^XC , ^xki — значение i-го

X — (x., x2 ,K, x„)                       , разряда входного вектора 1 2 n , определяющего k-ое значение реализуемой функции f(X) — p, p G {0,1,2,K •k - 1}, Ppa — a-й квазипорог нейрона, при котором f (X) — p

.

Xn

Определим удалённость заданных точек X от    c равного 0, , ,k , в рассматриваемом случае k=n=3, следовательно,

. Сведём вычисление

R (Xc, X)                              .

удалённости, определяемые радиусом      ^{c i} в табл.1, при этом следующей строкой

R ( X_c , X )

после строки, в которой указаны радиусы,     c i , является строка, в которой вычислена мощность сигнатуры графа, определяющего противоречивость реализуемой функции на орбите.

Точки пространства, вошедшие в противоречивые пары {010, 201}, {021, 201}, {102, 001}, отличаются друг от друга значением переменной x1. Соответствующие модели разностей значений векторов по x1 не равны друг другу, следовательно орбитальный центр X c = 002 является разрешённым.

Расщепляем переменную x ¹ :

f ( x j = 0 ^ х_г : 0002,

0010,

0021, 1102; f ( x , ) = 1 ^ x : 0001, 2201, 2220; f ( x j = 2 ^ x_z :0000, 2221,

X

В результате получаем распределение точек функции по орбитам относительно c = 0002 (табл. 2).

Табл. 1. Вычисление удаленности

Х с	f ( X ) = 0				f ( X ) = 1				f ( X ) = 2
	002	010	021	102	001	201	220		000	221
000	2	1	3	3	1	3	4		0	5
	{010,001}, {021,201}, {102,201} е U пр ,							U пр	= 3
001	1	2	2	2	0	2	5		1	4
	{002,000}, {010,201}, {021,201}, {102,201} е U пр , U пр = 4
002	0	3	3	1	1	3	6		2	5
	{010,201}, {021,201}, {102,001} е U пр ,							Uпр	= 3
010	3	0	2	4	2	4	3		1	4
	{002,220}, {021,001}, {102,201}, {102,221}, {201,221} е Uпр ,									U пр = 5
102	1	4	4	0	2	2	5		3	4
	{010,221}, {021,221} е U пр , U пр = 2

Продолжение Табл. 1.

X C	f ( X ) = 0				f ( X ) = 1			f ( X ) = 2
	002	010	021	102	001	201	220	000	221
221	5	4	2	4	4	2	1	5	0
					и „р >  2
222	4	5	3	3	5	3	2	6	1
					U „р >  2

Табл. 2. Распределение точек функции по орбитам

f ( X ) = 0				f ( X ) = 1			f ( X ) = 2
0002	0010	0021	1102	0001	2201	2220	0000	2221
0	3	3	2	1	5	8	2	7

X

Выбираем орбитальный центр   c , для которого мощность сигнатуры графа противоречивости минимальна  пр

, таким центром является

^Xc , ^Xc = 102.Орбитальный

X пара точек {021, 221},

центр   c = 102 является запрещённым, так как нашлась отличающихся друг от друга только переменной x1 , по которой

1        1         1         1                      .   Следовательно, при   любом расщеплении переменной x1 точки 021 и 221 останутся на одной и той же орбите, и отношение противоречивости останется:

f ( 0,2,1 ) = 0 , f ( 2,2,1 ) = 2 .

Рассмотрим орбитальный центр X c = 002, для которого пр^

(рис. 13).

010 021 102

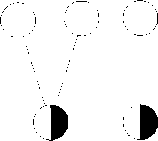
201   001

Рис. 13. Орбитальный центр Х С

Получим одно противоречие

{ 1102,0000 } е U „р

для его устранения достаточно

переменную ^{x 1} расщепить трижды:

V —X v' v" v^m Х 1    л Х 1 , Х 1 , X 1

В результате получаем распределение точек пространства, в которых определена заданная функция

f ( x_p x 2 , x 3

) , по орбитам (табл. 3).

Табл. 3. Распределение точек пространства

f ( X ) = 0				f ( X ) = 1			f ( X ) = 2
00002	00010	00021	11102	00001	22201	22220	00000	22221
0	3	3	3	1	7	10	2	9

Мощность сигнатуры графа противоречивости равна 0. Следовательно, полученная орбитально непротиворечивая функция f ⁽ x¹, x¹, x¹, x 2 , ^{x 3} ) эквивалентирует заданную функцию f ⁽ x ¹’ x ^2, x ³ ) , которая реализуется на сотовом нейроне с весами синапсов w¹ = 3 , w 2 = ^w 3 = 1, при этом квазипороги фаз равны номерам орбит, на которых расположены T = { 0,3 } T = { 1,7,10 } T = { 2,9 } соответствующие точки: ^{0 a}        , ^{1 a}           , ^{2 a} .