Рассмотрена проблема выбора эффективной архитектуры распределенной вычислительной сети для параллельного решения сложной задачи. Предлагается аналитическая.модель функционирования вычислительной сети типа клиент-сервер, построенная средствами теории массового обслуживания. Разработан метод оценки производительности вычислительной сети рассматриваемого типа, позволяющий учитывать характеристики решаемой задачи.

Проектирование сложных систем представляет собой итерационный процесс, когда на каждой последующей стадии выполняется доработка и детализация предыдущей версии проектируемой системы. В силу этого на первоначальном системотехническом этапе проектирования распределенную вычислительную сеть (РВС) целесообразно рассматривать как абстрактную вычислительную систему, состоящую из вычислительных узлов, объединенных каналами связи. Выбор эффективной структуры РВС определяется назначением системы, а также требованиями к ее производительности и надежности.

В ходе проектирования РВС, предназначенной для эффективного распределенного решения сложной задачи, требуется согласование структуры вычислительной сети со структурой параллельно выполняемого алгоритма решаемой задачи. В вычислительном смысле эффективной является методика крупноблочного распараллеливания алгоритма сложной задачи: разработка параллельного алгоритма, состоящего из идентичных последовательных ветвей, слабо связанных по данным и сравнимых по количеству операций. Одним из конструктивных приемов крупноблочного распараллеливания является распараллеливание по циклам, когда отдельные ветви алгоритма параллельно реализуют вычисления всех итераций одного цикла [1].

Крупноблочное распараллеливание алгоритма решаемой задачи хорошо согласуется с использованием клиент-серверной архитектуры для организации взаимодействия вычислительных узлов РВС в процессе решения задачи. На клиентах запускаются процессы, циклически реализующие вычисления по параллельным ветвям алгоритма; сервер, в свою очередь, реализует логику управления параллельными процессами, информационный обмен между ними, а также интерфейс с пользователем.

Обеспечение требуемой производительности РВС в процессе системотехнического проектирования сводится к оценке производительности исследуемых вариантов построения системы, а также к оптимизации структуры и режима функционирования для достижения заданной производительности при минимальной стоимости системы. Основным инструментом при исследовании производительности являются модели производительности вычислительных систем, позволяющие к тому же оценивать характеристики вычислительных процессов и использования ресурсов. Указанные характеристики необходимы для выявления факторов, влияющих на производительность, а также узких мест и недоиспользованных ресурсов.

Построим аналитическую модель производительности клиент-серверной РВС, состоящей из произвольного количества типов клиентов, произвольного числа клиентов каждого типа и многопроцессорного сервера.

Характеристики моделируемой РВС:У- количество типов клиентов; т - количество клиентов z-го типа ( i = 1, N ); и - количество однородных процессоров сервера; to - быстродействие клиентов z-го типа (FLOPS); to _$rv - быстродействие процессоров на сервере (FLOPS); и . - быстродействие канала связи клиентов z-го типа с сервером (бит/с).

Характеристики решаемой задачи: NO_al$ - средняя вычислительная сложность (количество машинных операций) одной итерации вычислений на одной ветви алгоритма решения задачи (оп.); NO_ctrl - средняя вычислительная сложность алгоритма управления одной ветвью алгоритма решения задачи (оп.); V_al$ - средний объем данных клиент-серверного обмена (бит); Т_№ - максимально допустимое время решения задачи.

Процесс функционирования РВС можно рассматривать как последовательную смену состояний на некотором интервале времени А / и применить для описания данного процесса аппарат теории массового обслуживания. Представим процесс функционирования РВС замкнутой системой массового обслуживания (СМО) с ожиданием и случайным распределением заявок всех типов по всем процессорам сервера без взаимодействия между собой. Пусть имеется N типов клиентов, причем количество клиентов каждого типа произвольное (т₁, т₂, ..., тД. Каждый клиент в некоторые случайные моменты времени нуждается в обслуживании. Обслуживание осуществляется посредством и однородных процессоров сервера. Поток заявок на обслуживание от клиентов ка ждо го типа - пуассоновский с параметром % . , где i = 1, N . Интенсивность обслуживания каждой заявки подчиняется экспоненциальному закону распределения с параметром ц . . Вновь поступившая на обслуживание заявка направляется с равной вероятностью на любой из свободных процессоров сервера и принимается на обслуживание. Если все процессоры заняты, то поступившая на обслуживание заявка становится в очередь и ждет своего обслуживания. Дисциплина обслуживания - случайный равновероятный выбор из очереди.

Рассматриваемая СМО может находиться в следующих состояниях:

• - a 0,0 0 - в системе заявок на обслуживание нет, все процессоры сервера свободны;

  1,0

  • -    а 10 о ^{_ в} системе находится одна заявка от клиента первого типа, на одном процессоре сервера обслуживается одна заявка, очереди нет;

  • -    ^а 0 ⁰ 1 - в системе находится одна заявка от клиента ^-го типа, на одном процессоре сервера обслуживается одна заявка, очереди нет;

  • -    a k ’¹ , j -в системе находится./заявок от клиента .-го типа, где N = 1, 2,..., N, к процессоров сервера занято обслуживанием, l заявок находятся в очередях на обслуживание;

  _h , M - h       _

  • - а ’ -в системе находится т . заявок от кли- m^ m 2 ,..., m ,

  ентов каждого типа, h процессоров сервера занято обслуживанием, (М-h) заявок находятся в очередях на обслуживание, где М- суммарное число клиентов:

  n , пр9 M >  n

  M, пр9 M <  n

  
  

  -Ph , ^{M -} h m 1 , m ₂,..., m N

  dt

  
  

  =- X

  
  

  h , M - h N M ;P’ _

  
  

  ,...

  
  

  m 1 , m ₂,.

  
  

  ■, m N

  
  

  C t ) +

  
  

  , h , M - h - 1

  
  

  +Л1 P‘ .

  ¹   m 1 - 1, m ₂,...

  
  

  +л₂ P ^h , ^{M -} h ^{- 1}

  ² m 1 , m 2 - 1,..., m N

  
  

  C t ) +

  , ^m N

  
  

  C t ) + ■■■+

  
  

  h , M - h - 1 +Лдт P             ( t ).

  ^N m_p m 2 ,..., m N - 1

  j i , ^пр9 j <  ^k

  .

  k , ^пр9 j, >  k

  При условии

  
  

  N

  M = X m i ; h = i = 1

  
  

  k = 0, h ; I = 0,( M - k ) .

  Используя правила составления системы дифференциальных уравнений, запишем систему дифференциальных уравнений рассматриваемой СМО в виде [2]

  dl>0,0

  -P^=1 m^b ct)+Mi •"C

  dti

  ^{+ M} 2 ^P 0J⁰...,0 ^C t ^{) +} - ^{+ M} N ^P 0’0,...,1 ^C t ⁾

  
  

  C i = ^Л^ < 1                       (1)

  ^M i существует стационарный режим, а функционирование СМО описывается системой линейных уравнений. Исходя из условия существования стационарного режима (1), определим соотношение параметров вычислительной

  
  

  системы ю . , to_srv и V . , при котором выполняется условие стационарности исследуемой СМО.

  Параметры потоков % . и ц . зависят от величин Т_о . и т . , где Т_о . - среднее время между заявками клиента .-го типа, которое представляет собой среднее время выполнения одной итерации алгоритма на клиентах .-го типа и зави

  
  

  сит от аппаратной реализации клиентов .-го типа, а также

  
  

  -P k ’ l (t)

  ^j 1 ,j 2 -j dt

  
  

  N

  - X

  i = 1

  
  

  ^[( mi - ji )л i + - i M i ] P ^k ’ ^{1    (} t ) +

  ^j 1 ^,j 2 ,,jN

  +( m - j 1 + 1)Л 1 n-k + i P ^k - J, ¹    W

  n       J 1   ,J 2 Hn

  
  

  от заданного параметра задачи NO_ali;: ^NO a ^l K

  ^T 0 i =-------- ,

  Щ

  
  
  
  

  где т . - среднее время обслуживания заявки клиента .-го типа, которое зависит от аппаратной реализации серве

  
  

  ^{+ ( m} 2 ^{- j} 2 ^{+ 1) л} 2          P k 1 l i   / ^C t ^{) +} ■■■ ⁺

  n j 1 ^, J 2 ,...., ^j N

  
  

  ,        ■    1 \ n - k +1 k k -1 1 z x

  ^{+ ( m} N ^{- j} N ^{+ 1) л} N         P ;    ; -1^C t ^{) +}

  n         JpJ 2 ,..., jN

  
  

  ра, пропускной способности каналов связи, а также от заданных параметров задачи NO_al$ и K_alg:

  4 ? = ^ rnsi ⁺ 4 jrv ^,

  
  

  ^{+ ( m} 1 ^{- j} 1 ^{+ 1) л} 1 — ^Pk 1 1¹ j ^C t ^{) +}

  n Ji    , J 2 ^,...^, JN

  ^{+ ( m} 2 ^{- j} 2 ^{+ 1) л} 2    P k ’ / 11 i ^C t ^{) +} ■■■ ⁺

  n j 1 ^, J 2     ,..., JN

  ^{+ ( m} N ^{- j} N ^{+ 1) л} N ~ ^Pk ’ li ¹ i -1 ^C t ^{) +} n ^jV J 2 ,..., JN

  
  

  Ф тпз i

  
  

  ^V a ^lg  A

  , 4 srv

  ^V i

  
  

  NO ctrl

  , Щ srv

  
  

  следовательно,

  ,    ^Va lg    NO Ctrl

  4 i =      +     ctr¹-

  ^V i     Щ srv

  
  
  
  

  +

  

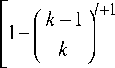
  ^- 1 ^M 1 ^P k + 1 + 1 2

  
  

  Интенсивность потока заявок на обслуживание представляет собой среднее число заявок, поступающих в единицу времени, поэтому 1 . определяется по формуле

  
  

  , ^jN

  
  

  C t ) +

  
  

  ____¹ ____=

  I • T 0 i - I • 4 i ^T 0 i - 4 i

  
  
  
  

  +

  

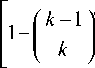
  d 2 ^M 2 j t 1,..., j N ^C t ^{) +}

  
  

  где I- среднее количество итераций на одной ветви алго

  
  

  +...

  

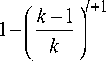
  ^-N ^M N P k , lt-jP + 1 ^C t ^{) +}

  
  
  

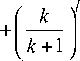
  d 1 ^M 1 P k +1: lN

  k ^l

  
  

  ■, ^j N

  
  

  C t ) +

  
  

  + L,—7 d 2 ^M 2 ^P , /+1 j ^C t ^{) +} ■■■⁺ I k + 1 ^              / 1 , j 2 ^{+ 1,}...^, JN

  
  

  ритма решения задачи.

  Интенсивность обслуживания заявок - это величина, обратная среднему времени обслуживания заявки, следовательно, т . определяется по следующей формуле:

  m ? = Т.                       (⁵)

  4 i

  С учетом выражений (1), (4) и (5) для существования стационарного режима необходимо выполнение следующего соотношения:

  < 1 .

  ^T 0 i ^- 4 i

  
  

  Произведя преобразование, получим соотношение параметров Т_о . и т_р при котором выполняется условие существования стационарного режима

  
  

  T oi ^ 2 -т i . (6)

  Подставляя в условии (6) выражения для T и т . из уравнений (2) и (3) соответственно, получаем соотношение параметров вычислительной системы ol щ _$гу и V . , при котором выполняется условие стационарности исследуемой СМО

  
  

  система линейных уравнений (8) является полной и имеет единственное решение. Так как в системе (8) N

  L J i = ( k + 1 ) , то индексы к и / в обозначении вероятно- i = 1

  сти можно опустить.

  Для решения системы уравнений (8) в общем виде сделаем подстановку:

  
  

  Ш <

  
  

  ^ш згр

  
  

  ^V i • ^NO a / _g

  ² V a,   ’

  >     ^{2 N}O ctrl • Ш ’^V i

  
  

  N

  ^. j ,.... j , = П P j. i = 1

  
  

  (Ю)

  
  

  .

  
  
  
  

  и запишем систему уравнений в следующем виде:

  
  

  ^V i • NO a /g

  
  

  ^{— 2 V} a / g ’^ш

  
  

  _—

  
  

  При выполнении условия (7) система линейных уравнений, описывающая функционирование СМО, с учетом Q_{k /} - вероятности того, что в системе находящейся в состоянии а _р после обслуживания одной из к + / заявок общее число заявок, ожидающих обслуживания в очередях, не изменится, имеет следующий вид:

  N

  
  

  N

  L ^{( m} i ^{— j} i ^|J i ⁺ d i ^M i

  , i = 1

  
  

  ~

  Pj.

  
  

  ~    ~

  - Pi - еее - Pi   +

  ^j 2           J\N

  
  

  —У m л, P0 ^0,0 А^ ^{1 1} 0,0, е i = 1

  ^{+ М} 2 P OXeeO ⁺ • •

  
  

  , 0 ^{+ М} 1 ^Р 1Деее,0 ⁺

  
  

  • • ^{+ М} N P GAeeej = ⁰ ’

  
  

  N

  ^{[ —} L ⁽ m i ^— j ^)л i ⁺ d i M ] P k j i = 1

  
  

  ⁺

  ¹2 ^,...^{, j} ,

  
  

  ,      . ex П — k + 1 k — - 1 l

  ^{+ (} m l ^— j 1 ^{+ 1)л} 1           P j _{— i} j

  
  

  n ^J' n — k +1

  ■■■ ⁺ ( m N ^— J n ⁺ 1 ) ^л N ^P .

  
  

  ,^еее, ^j ,

  
  

  +

  
  

  n

  ^{+ (} m l ^{— J} 1 ^{+ J ) л} 1 - P k ^{, l}_ 1 1 n j ^J j

  
  

  , k — 1, l Д ^J 2 ^,еее^, j ,

  
  

  — 1 ⁺

  
  

  ,еее,

  
  

  ⁺

  ’ ^j N

  
  
  
  

  еее

  
  

  ^{+ ( m} N ^{— j} N ^{+ J ) л} \ P k ^{, l}j ¹ n J\ , J 2 ,".

  
  

  •^{, J} n

  
  

  — 1 ⁺

  
  

  ~

  
  

  +

  
  

  +

  
  

  1—

  
  

  1—

  
  

  k — 1) ^{l + 1}

  
  

  k

  
  

  .l + 1

  
  

  k

  
  

  k +1

  
  

  d 1 M 1 ^P k + ^l + J ,.

  
  

  . еее ।

  
  

  + еее

  ^{, j} ,

  
  

  > k , l + 1         +

  J p ^j 2 ^,еее^, j , ^{+ 1}

  
  

  ^l

  I d 1 ^M 1 P k +1, j .., J n

  
  

  • ее +

  
  

  ^l

  +| — d_NM_NP ^{k + 1, l} . ^.= 0, Lt+l । ^{N N} j„ j 2 ,еее, j, ^{+ 1}

  
  

  • h , M — h     .

  N M P      +

  ^, i m ! , m 2 ,еее, m ,

  • -■ . yr p h , M — h —1 i =1 +л1 P

  ¹ m , — 1, m 2 ,..., m.

  
  

  ... +

  +л₂ p h ^, M ^— h ^{— 1} +

  ² m , ,m 2 — 1, m ,

  
  

  +л_№ P h , ^{M —} h ^{— 1 N}  m , ,m ₂,еее, m ,

  
  

  . ... .

  
  

  — I

  
  

  ■ 1 = О

  
  

  С учетом условия нормировки 0,0 ^Р 0,0,еее,0 ⁺

  h M — k k + 1 k + 1 — j , k + 1 — R

  + L L L L - L P k ^, j

  k = 1 l = 0 j , = 0 j 2 = 0     j , — , = 0 ¹

  
  

  ^,еее^, j, ^^^k + ^l — ^R )

  
  

  n — k +1 ~

  ^{+ (} m i ^— J i ^{+ 1)л} 1------- ^pj —

  n ¹

  n ^— k ^{+ 1}

  ... ^{+ ( m} N ^{— J} N ^{+ 1)л} N n

  
  

  ~    ~

  - Pi - еее - Pi  + еее

  J 2         J N

  
  

  ~

  P J 1

  
  

  ~    ~

  •P • p 1 +

  ^P j 2 ^еее P J , ^{— 1 +}

  
  

  k ~   ~

  ^{+ (} m l ^— J i ^{+ 1)л} 1- ^P j — 1 ^{- P}N 'е n ^{J1        J2}

  _           _ k ~ ~

  ... ^{+ ( m} N ^{— j} N ⁺ .)^л N~ ^Pj, ^{- P}L

  n ^{1 2}

  
  

  •P + еее              еее

  j_N ~

  • P 1 + >  - Pj, ^{— 1 +}

  
  

  +

  
  

  l + 1

  1+| — 1 I k I

  
  

  ... +

  
  

  l + 1 1+f kk — ¹ 1 I k I

  
  

  k ) ^l

  
  

  k +1

  
  

  k

  
  

  k +1

  
  

  ~   ~

  
  

  d l M i P j , + 1 - P j 2 -

  
  

  ~

  ...P;

  ...            ...

  j_N

  
  
  
  

  ~ ~

  
  

  ~

  
  

  d N ^M N ^P J 1 ^{- P} j 2 ^- -^{- P} j , + 1 ⁺

  
  

  ~   ~    ~

  d l M i P j + 1 - ^P j 2 - ... - ^Pj , + ...

  
  

  l

  ~ ~    ~

  d N ^M N P J , ^{- P} j 2 ^- - ^{- P} j , + 1 = ⁰ .

  
  

  Перегруппируем систему (11) таким образом, чтобы

  
  

  Pj. входили в соответствующие выражения, содержащие т . , 1 . , ц . , т. е. произведем разделение переменных по индексам, после чего она примет вид

  
  

  n ^— к ^{+ 1}

  ^{( m i — j , + ^1)л 1--------

  
  

  n

  
  

  ~ P J 1 — 1

  ~

  
  

  ^^^^^^е

  
  

  ^— [ ⁽ m l ^— . 1 ^)л 1 ⁺ d i ^M i ] ^pj , ^{+ + (} m l ^— J i ^{+ 1)л} 1 ^{k p} j — 1 ⁺ n ¹

  
  

  +

  
  

  1—

  
  

  k — 1) ^{l + 1}

  
  

  k

  
  

  ~

  ^d 1 ^M 1 ^pj , + 1 ⁺

  
  

  l

  k ^   ^ ^   ^

  k +J I d i ^M 1 P i + l } Pj, ^- Pj,-Pj, +

  
  

  n — k +1 ~

  ^{+ {( m} 2 ^{— J} 2 ^{+ 1)л} 2          ^P J , — 1

  n ²

  — [ ⁽ m 2 — J 2 )л 2 + d 2 M 2 ] P j ₂ +

  +⁽ m 2 — j 2 + ¹⁾ л2 k Л-1 + n ²

  
  

  +

  
  

  1—

  
  

  k — 1) ^{l + 1}

  
  

  k

  
  

  ^^^^^^е

  
  

  ~

  d 2 ^M 2 ^P j ₂ + 1 ⁺

  
  
  
  

^l ~   ~ ~   ~

+^    ) d2М2 Pj^+1} Pj'' Pj^   PjN+ ™+ n - к +1 ~

+{ (mN - jN + ') Л N       Pj -1 - nN

~

- [(mN - jN )л N + dN ^N ] PjN + к ~

^{+ (} m N ^- j N ^{+ 1) л} N PPi - 1 ⁺ n^N

+

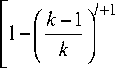
~ dN МNPjN+1 + l к        ~   ~ ~   ~

⁺ |        d N М N P i + 1 } P j ' P j ''' j , = ⁰

N              1          2             N - 1

Система линейных уравнений (12) будет иметь решение только в случае, когда выражения в фигурных скобках равны нулю, так как Pj ^ 0 . Следовательно, можно записать n - к +1 ~

^{( m} 1 ^- j 1 ^{+ 1)Л} 1-------- P j - 1

n       ^J1

^- [ ^{( m} 1 ^- j ' ^)Л ' ^{+ d} 1 ^M 1 ] P j ⁺

-

к ~

^{+ ( m} 1 ^- J 1 ^{+ 1)Л} 1 - P j - 1 ⁺ n ¹¹

+

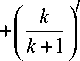
~ d1M1 Pj+1 = 0,

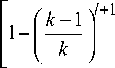
~ d1M1 Pi+1+ нений рассматриваемой СМО для стационарного режима имеет следующий вид:

^{m с Р} 0,0 = ^Р 1,0 ,

Кm - к - 1)с + к ] рк, 1 = n - к +1

= (m - к -1 + 1)с-------Рк-11 + n , k

+(m - к -1 + 1)с — Рк i-1 + n , kl

⁺ ;          ^Р к + 1, i ⁺

( ^к +1 ) l ¹

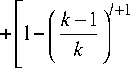
кРк, 1+1, mPM ,0

n - m + 1 _n

= с         PM-1,0, n, где pfc t - вероятность нахождения СМО в состоянии, при котором к заявок обслуживаются и / находятся в очередях и ждут обслуживания, с = Л, к = 0, n, 1 = 0, m - к.

M

В результате последовательного решения системы уравнений (14) получим новую систему уравнений для определения вероятностей Р_{к i} вида

^Р 1,0 = ^{m с}' ^Р 0,0 ,

n - к +1 ~

(mi - ji + 1)Лi--------Pj -1 - ni

~

-[(mi- j)Л i+di Mi] Pj + i m - к -1 +1 n - к +1

Рк, 1 =------,------с---------рк-1,1 + kn m - к -1 +1 к

⁺----- 1 -----с- ^Рк , 1 - 1

kn

,          ,x к ~

+(mi- ji+ 1)Л i  P -1 + ni

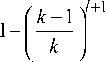
~ di MiPj+1 +

~ di MiPj+1

+

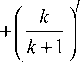
= 0, n - к +1 ~

(mN - jN + 1)л N        Pj, -1 - nN

~

- [(mN - jN )лN + dNMN] PL +

N к ~

^{+ (} m N ^- j N ^{+ 1) л} N ~ ^Pj„ - 1 ⁺ n^N

₌ n ^- m ^{+ 1 P} m ,0      ^{с           P} m - 1,0 .

m n

Следовательно, для определения вероятностей Р_{к i} достаточно решить систему уравнений (15), последовательно выражая вероятности Р_{1 ;}, Р_{к (}, Р_{т 0} через Р_{о 0}.

Сделав соответствующие преобразования по схеме, реализующей метод индукции, получим решение в общем виде. Используя условие нормировки h m - к

Р 0,0 + ZX Р к , 1 = 1 , к = 1 1 = 0

найдем выражение, позволяющее определить вероятности Р, .состояний СМО:

к, ;

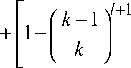
~ dN MNPjN+1 +

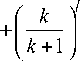
~ dNMNPjN +1 = 0-

Каждое уравнение системы (13) представляет собой систему уравнений СМО, состоящую из т источников заявок (клиентов) одного типа и и обслуживающих приборов (процессоров сервера). Система линейных урав

Р к , 1 =

< к + 1 -1"

I ¹ ,

n m - i i=0j=0

ⁿ ) ^m !        ¹ _с ( к + 1 )

к ^ ( m - к - 1 ) _n ^{( к + 1} )

i + j -1 j

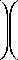
ⁿ )_____ m !'

j J ( m - i - j )! n ⁽ i ^{+ j} )

_с ( i + j )

| n , np9 m >  n , где h = (

[ m , np9 m <  n .

Отсюда следует, что выражение для решения системы уравнений (13) будет иметь следующий вид:

x

~   (k + 1 -1)

P, = I

j* I 1

h M - k

1 cp = ДД P k . 1 '1 ,             (20)

k = 1 1 = 1

n ^ m ? !       1

^k J⁽ m i ^- j ,' )^! n ^{( k + 11}

^е jPoi

0 i = 1 +

1 cp 4 ?

T oi + 4 ?

m x- ~ причем Д Pj ^ 1. Осуществляя обратную подстановку j, =0

выражение (16) в (10) с учетом количества путей х(k+1).j достижения состояния ak’1.   . , что в общем случае j 1. J 2.-. j« соответствует полиномиальному коэффициенту, равному

_ ( k + 1 )!

^{Х ( k + 1} ). j - = N ’ П j ! i = 1

N где (k +1) = 0.1..... Д j-, получим

? = 1            *

Pk.1     =    ~ = j1. j 2..... j*    П j- i=1

Тогда среднюю производительность РВС можно определить, используя выражение

N

П ер = Д ш . ^ ?- •                (22)

i = 1      ⁰ ?

Для оценки производительности системы по выражениям (20), (21) и (22) необходимо вычислить вероятности Р ^ _г При выводе выражения (19) дляР ^, _; предполагалось, что потоки запросов на обслуживание являются простейшими с параметрами X, а время обслуживания запросов клиентов z-го типа сервером подчиняется экспоненциальному закону распределения с параметром ц . . Для реальных вычислительных систем потоки отличаются от

k + 1 -1 l

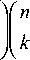
) 1

n ^{( k + 1} )

^m i ^!

( k + 1 )! ^X N

П j !

i = 1

В данном случае нормировки (9)

N

П i =1

⁽ mi^- Ji ^)!

p j, p⁰.^{0 c} i P 0.0.....0 .

0.0

P 0.0.....0 определяется из условия

пуассоновских и экспоненциальных и зависят от архитектуры вычислительной системы и параметров выполняемых на ней алгоритмов [3]. Для РВС рассматриваемого типа в соответствии с выражениями (2), (3) и (4) значение параметра интенсивности X . вычисляется по формуле

_              ‘ 1

Л? = NOa ;8   Va ;к   NOct; ’ ш?       v ?      ш,,,.

p ⁰.⁰

P 0.0.....0 =

- 1

h M - k

Д Д k =1 1=0

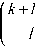
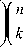
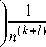
( k + 1 )!

N

П j , !

Д П

.j = 0. m, i = 1

m i ^!     _c j

⁽ m i ^- Ji ^)! ?

где/ 1,2,3, ...,N.

Параметр интенсивности обслуживания ц . определяется выражением

1 ^м ? = 77------------- .

Va ;g + NOctrl v i     ш$г.

.i 2 = ⁰. m 2

.i = ⁰. m.

Проведя подстановку условия (18) в (17), получим решение системы уравнений в общем виде

Р k. 1      = j„ j 2.-2 j„

Полученное значение средней производительности РВС П_ср позволяет оценить среднее время решения задачи Т_ср в проектируемой распределенной вычислительной сети:

Т ер

^NO a ; _к П ер

I k + 1 - 1Y n ^ 1 ( k + 1 ) ! *     m, !      i

? 0 j^-

I 1    II k L^{( k + 1} ) *    ^П( m - j )i ?

n ii j ! -=1     -      - i=1

Предложенный подход позволяет осуществлять выбор эффективной структуры по производительности РВС, настроенной на решение сложных задач определенного

h M - k

ДД k=1 1=0

k + 1 - 1

l

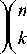
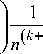
( k + 1 ) !

N

П j !

i = 1

N

ДП i,=0. mx i=1

mi

mi

-

! j J i )!^{P j}

класса с заданным ограничением на допустимое время решения Тдоп.

^j * = ⁰. ^m *

При оценке производительности РВС определяющим оказывается общее количество заявок, находящихся на обслуживании и в очередях, независимо от их типа. Об

щее количество заявок, находящихся в очередях, можно

определить, используя понятия совокупности стационарных вероятностей Р^ _р средней длины очереди ; и коэффициентов 0 . средних потерь производительности для клиентов каждого типа:

k + 1 k + 1 - J 1 k + 1 - R

P k . = 2 Ду 2 JJ j._Лk + 1 - R ) , (19) J 1 = ⁰ j 2 = ⁰     j * ^{- 1} = ⁰