Проектирование зубчатой передачи внутреннего зацепления с малой разностью чисел зубьев. Объектно-ориентированный подход

Разработка программ с большим количеством объектов и программных модулей требует проведения объектно-ориентированного анализа расчетных моделей и объектно-ориентированной декомпозиции задачи. При этом не существует общепризнанного наилучшего способа проведения декомпозиции, но в ряде источников [1; 2] при создании моделей рекомендуется заострять внимание на сущностях, характерных для исследуемой предметной области, в данном случае на зубчатых парах (рис. 1).

Проектирование зубчатых передач (ЗП) по заданным показателям качества является достаточно сложной технической задачей. При декомпозиции данного процесса можно выделить следующие основные объекты: объект с параметрами зубчатого колеса (профиль, возможно, параметры ступицы и др.), объект с параметрами зубчатой передачи (к таковым можно отнести межосевое расстояние), объект с моделью описания профилей зубчатых колес, объект с алгоритмом вычисления граничных условий кривых, образующих профиль зубчатого колеса, объект с алгоритмом для выполнения анализа зубчатой пары (нахождение точек контакта, получение углов вхо-да/выхода из зацепления, получение передаточной функции, линии зацепления и др.), кроме того, объекты для импорта/экспорта геометрии зубчатых пар в другие программные продукты. Также при решении задачи разработки программного обеспечения необ- ходимо выделить служебные объекты, позволяющие наращивать базовый функционал и осуществлять адаптацию под требуемую задачу или CAD/CAE-среду. По многообразию используемых сущностей и их свойств можно судить о сложности разрабатываемого программного обеспечения.

После проведения объектно-ориентированной декомпозиции была создана объектно-ориентированная модель (рис. 2), на основе которой был разработан программный комплекс для синтеза геометрии и моделирования взаимодействия зубчатых пар GearAnalysis.

В данную объектно-ориентированную модель заложен функционал обеспечения синтеза геометрии разномодульных зубчатых пар внешнего и внутреннего зацепления, позволяющий выполнять визуальное моделирование взаимодействия зубчатых пар и подключать дополнительные программные модули, например, программный модуль для экспорта геометрии в CAD-среду. Таким образом, можно сделать вывод, что данная объектно-ориентированная модель дает возможность решать задачи автоматизированного проектирования зубчатых передач с применением плагинов автоматизированной передачи зубчатых колес с наиболее приближенным профилем в CAD/CAE-среды для проведения компьютерных анализов работоспособности зубчатых передач и включения в состав проектируемых изделий.

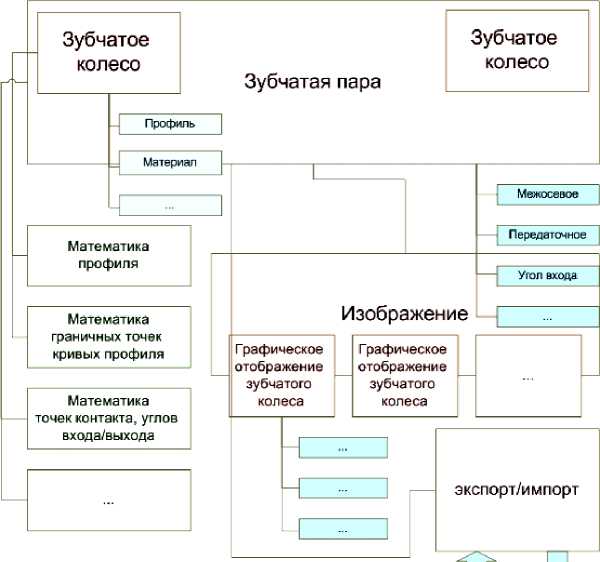
Рис. 1. Схема объектно-ориентированной декомпозиции процесса синтеза геометрии зубчатых пар

В разработанном программном комплексе предусмотрена как возможность использования стандартных эвольвентных зубчатых профилей [3], так и возможность варьировать параметры профиля с целью получения нестандартных профилей с последующим их анализом. Такими нестандартными профилями могут являться профили, полученные по параметрам профилей втулки или вала со шлицевым эвольвент-ным профилем [4], а также подобранные к ним зубчатые колеса, имеющие стандартный эвольвентный профиль, с варьируемыми коэффициентами высоты зуба, смещения и другими параметрами.

В основу алгоритма программного комплекса заложены разработанные авторским коллективом математические модели, описывающие профиль зубчатых колес и представленные в диссертационных работах [5; 6]. Данные модели основаны на применении теории огибающих кривых, позволяющих более точно описать геометрию профиля зубчатого колеса в сравнении со стандартным эвольвентным профилем. Представленные математические модели позволяют получить геометрию профилей как внешних, так и внутренних зубчатых колес.

Для подтверждения работоспособности зубчатой пары в программном комплексе реализованы механизмы анализа, которые дают возвожность вычислять расстояние между зубчатыми парами, находить точки контакта, углы входа/выхода в зацепление, вычислять радиусы кривизны профилей зубчатых колес в местах касания профилей. Это позволяет определять на этапе проектирования геометрические параметры, при которых возможно кромочное взаимодействие, и в ав- томатизированном режиме изменять параметры зубчатой пары таким образом, чтобы минимизировать воздействие данного фактора. Кроме того, реализован функционал для вычисления и построения передаточной функции зубчатой пары и линии зацепления профилей.

В состав программного комплекса вошел функционал, обеспечивающий возможность расширения базовых возможностей системы (см. рис. 2). Одним из таких модулей стал плагин plugin_solidworks.gap с реализацией функций экспорта геометрии получаемых зубчатых пар в CAD-среду SolidWorks. Данный программный модуль производит построение моделей зубчатых колес в среде проектирования SolidWorks и модели сборки зубчатой пары. Работа плагина реализована с применением технологии ActiveX для связи с CAD-системой SolidWorks 2007 средствами API SolidWorks.

Таким образом, использование программного комплекса, реализованного на базе предлагаемой объектно-ориентированной модели, позволит существенно снизить временные издержки на разработку изделий, в состав которых входят зубчатые передачи.

Для примера приведен один из вариантов использования подхода к проектированию зубчатой передачи с малой разностью чисел зубьев, в основе которой лежит приближенное зацепление внутреннего колеса планетарной передачи, нарезанное протяжкой с углом профиля 30° (модуль 2,5 мм) и шестерни, нарезанной стандартным инструментом с углом профиля 20° (модуль 2,25 мм).

TBaseFunctions2	Класс, содержащий методы, описывающие профиль зуба по теории огибающих кривых
	--

TParamProfile             Классы, хранящие параметры, описывающие профиль зубчатого колеса

		TParamGear
		TMathKernel	Родительский класс, содержащий базовый функционал для классов выполняющих математические вычисления
		TFrontierConditions	Класс, содержащий методы для вычисления граничных условий, функций описывающих профиль зуба внешнего колеса по теории огибающих кривых
	---► TFrontierConditionsForlnternal		Класс, содержащий методы для вычисления граничных условий, функций описывающих профиль зуба внутреннего колеса по теории огибающих кривых
	---►	TDistance	Содержит методы, предназначенные для нахождения расстояния между зубьями пары колес и для нахождения точек контакта
		TAnalysisOnePalr	Содержит данные и методы для анализа однопарного зацепления пары зубчатых колес
		TAnalysisTwoPair	Содержит данные и методы для анализа многопарного зацепления пары зубчатых колес
		TGraphicObject	Класс, содержит базовый функционал для классов системы отрисовки процесса взаимодействия пары зубчатых колес
		TGraphicObjecl_Gear	Содержит данные и методы отрисовки зубчатого колеса
		TG ra p h i cObjectAxi s	Содержит данные и методы отрисовки осей системы координат
		T GraphicObject_Circle	Содержит данные и методы отрисовки окружностей зубчатых колес, а так же точек контакта
		TGraphicArea	Класс, содержит методы и данные, обеспечивающие управление графическими объектами для визуализации процесса взаимодействия зубчатых пар
		TExportGearAnalysis	Класс, содержащий методы и данные, передающие необходимый функционал внешним объектам расширения функциональных возможностей приложения
		TExtensions	Класс, содержащий методы и данные, необходимые для подключения, функционирования и управления внешними объектами расширения функционала приложения

Рис. 2. Объектно-ориентированная модель приложения

Существующие методики расчета не позволяют получить работоспособную передачу с такими параметрами. В данной работе приведены результаты геометро-кинематических исследований планетарной передачи типа К-Н-V с малой разностью чисел зубьев и «разномодульным» зацеплением, на основе которых создана малогабаритная ручная лебедка. Модель такой передачи исследована с помощью предлагаемого программного комплекса GearAnalysis (рис. 3).

После синтеза геометрии в программном комплексе GearAnalysis с целью проверки работоспособности зубчатой пары с помощью программного модуля, входящего в состав программного комплекса plugin_solidworks.gap, был осуществлен экспорт геометрии и автоматизированное построение зубчатых колес в CAD-среде SolidWorks.

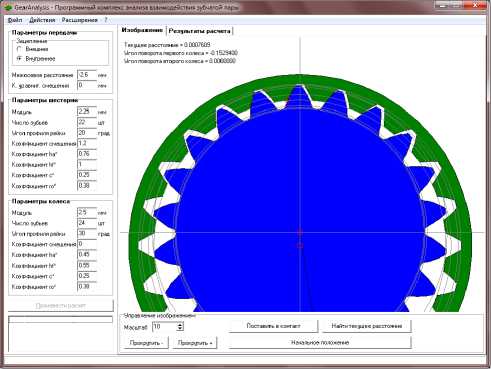
Рис. 3. Синтез геометрии зубчатой пары в GearAnalysis

Через систему SolidWorks твердотельные модели были экспортированы в инструмент для проверки работоспособности и исследования кинематики «разномодульной» передачи с выбранными параметрами MSC.VisualNastran Desktop (рис. 4).

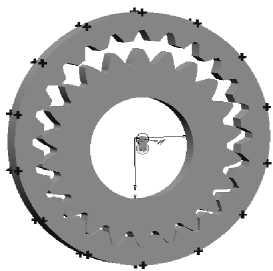
Рис. 4. Имитационная модель передачи в VisualNastran 4D

На кинематические характеристики разномодульной планетарной ЗП влияет несколько геометрических параметров профиля. Наиболее существенное влияние на передаточную функцию и значения передаточного числа передачи оказывают межосевое расстояние (эксцентриситет); коэффициент смещения на шестерне; коэффициент высоты головки зуба шестерни (для обеспечения собираемости передачи).

С помощью программного комплекса GearAnalysis были подобраны параметры, при которых передача существует и обеспечивается ее собираемость. Однако для качественной оценки параметров передачи требуется вычислительное моделирование.

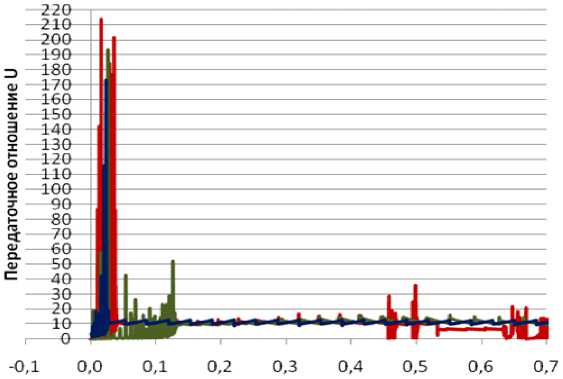
В результате численных экспериментов моделирования взаимодействия шестерни и колеса получены зависимости передаточного отношения U внутренней ЗП от времени t .

Параметры функций передаточного отношения ЗП соответствуют опытам 1, 2 и 3 (рис. 5).

Большие колебания передаточной функции в начальный момент времени – ошибка интегрирования, связанная с выбором бокового зазора при начале движения. В начальный момент времени передача не находится в зацеплении, следовательно, до контакта с колесом шестерня проворачивается вхолостую, при этом передаточное отношение стремится к бесконечности. Далее рабочие поверхности взаимодействуют, при этом происходит удар и отскок (в модели не учитываются деформации валов, смазка и опоры, существенно гасящие колебания), пока передача не достигнет установившегося режима (0,15 с на рис. 3). При этом колебания, возникающие в первом варианте передачи с 0,4 с, показывают ошибочность выбора параметров, так как в результате обкатки колеса на определенном шаге возникает заклинивание передачи, что вызывает резкие изменения передаточной функции. В реальности это приведет к подклиниванию передачи, а под нагрузкой возможно разрушение контактных поверхностей.

Рассмотрим график изменения передаточной функции во времени (рис. 6). Передаточная функция меняется во время контактного взаимодействия, при этом усредненное передаточное отношение составляет 10,85, а отклонение передаточного числа составляет 0,5 единиц и не превышает 5 %.

Исследование напряженно-деформированного состояния силового привода механизма лебедки выполнено с использованием пакета конечно-элементного моделирования Ansys. Решение контактной задачи – это высоконелинейный процесс, требующий большого количества итераций при проведении моделирования. Для снижения требуемого количества ресурсов и времени расчета задача взаимодействия моделировалась в двухмерной постановке с использованием конечных элементов типа Plane42 (см. рис. 6), содержащей 4 узла, и возможностью учета физической и геометрической нелинейности [7]. Задана толщина элемента 10 мм.

Время!, с

Ф-ия передаточного отношения ЗП с межосевым расстоянием 2,8 мм и коэф, смещения шестерни 1,25

Ф-ия передаточного отношения для ЗП с межосевым расстоянием 2,6 мм и коэф, смещения шестерни 0,6

Ф-ия передаточного отношениядля ЗП с межосевым расстоянием 2,75 мм и коэф, смещения шестерни 1,2

Рис. 5. Функции изменения передаточного отношения ЗП

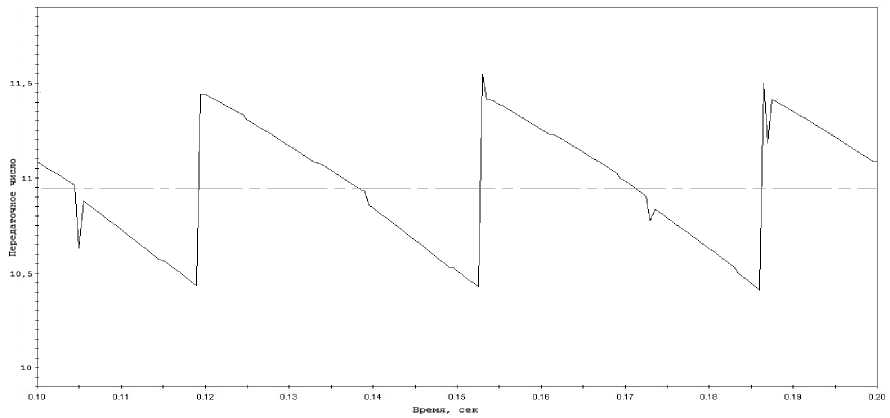
Рис. 6. График изменения передаточной функции пары с выбранными параметрами

Для получения достоверных результатов моделирования была модифицирована конечно-элементная сетка на контактирующих частях рабочих поверхностей зубьев. В качестве материала задана сталь 40Х со следующими параметрами: модуль Юнга: 2,1·10 ⁵ МПа, коэффициент Пуассона – 0,28, предел текучести – 700 МПа, плотность – 0,007 8 г/мм ³ .

Согласно проведенному кинематическому расчету, шестерня совершает сложное циклическое движение относительно колеса, что требует использования специальных конечных элементов, приводящих расчет к трехмерной постановке. Для решения данной проблемы был использован метод суперпозиций. В представленной модели колесо совершает вращение вокруг своей оси, а шестерни ограничены перемещением по оси вращения. В качестве нагрузки задан крутящий момент сопротивления 10 000 Н·мм в противоположном направлении от вращения колеса.

Для созданной модели был проведен динамический расчет с большим количеством итераций и учетом кинематики взаимодействия зубьев передачи. В результате моделирования получено распределение напряжений.

Наибольшие напряжения возникают в зоне контакта (рис. 7), что вызывает появление пластических деформаций в модели. Величина изгибающих напряжений зуба шестерни лежит в диапазоне 625…750 МПа, что близко к пределу текучести материала.

Распределение пластических деформаций в результате взаимодействия (рис. 8) показывает, что пластические деформации возникают в вершинах зубьев колеса и на боковых поверхностях зубьев шестерни. Величина деформации не превышает 16 % от первоначального размера для колеса и 4 % для шестерни, это означает, что пластическая деформация кромки вершины зубьев колеса идет более интенсивно, чем боковой поверхности шестерни. Пластическая деформация приводит к упрочнению боковых поверхностей зубьев за счет поверхностного наклепа [7].

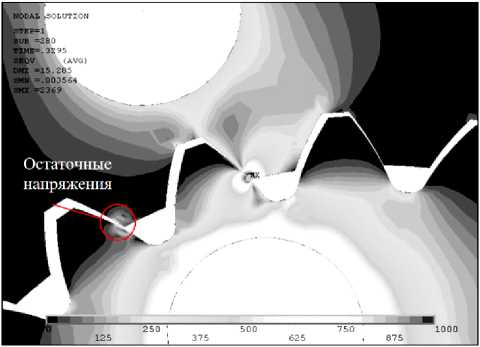
Рис. 7. Эквивалентные напряжения в процессе взаимодействия

В процессе работы передачи под нагрузкой возникает ситуация, при которой нагрузка перераспределяется между двумя зубьями. Это приводит к снижению контактных напряжений (рис. 9).

Большой коэффициент перекрытия в передаче достигается в основном за счет малой разности числа зубьев колеса и шестерни.

В результате проведенных исследований были получены величины действующих напряжений и деформаций зубьев в приближенном зацеплении зубчатой пары с кромочным взаимодействием. Показано, что даже в случае кромочного контакта при нагрузках, не превышающих номинальные, зубчатая пара прирабатывается, что может быть реализовано изготовителем как в процессе подготовки к эксплуатации, так и в условиях эксплуатации при выполнении соответствующих инструкций. Созданный образец с планетарной передачей типа К-Н-V, составленной из разномодульных колес, работоспособен, обеспечивает расчетные характеристики.

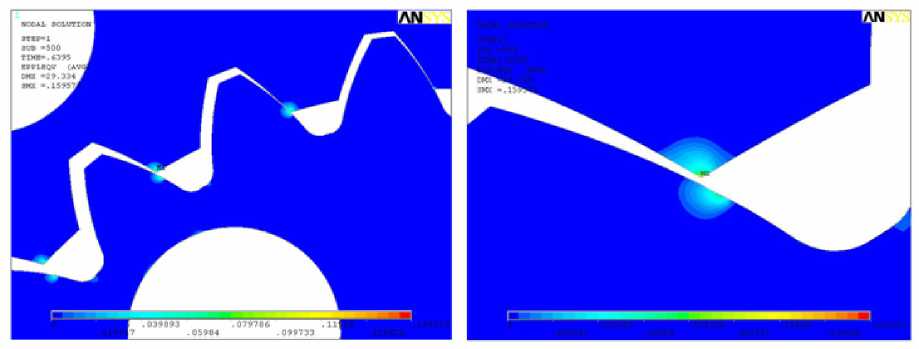
Рис. 8. Пластические деформации в модели

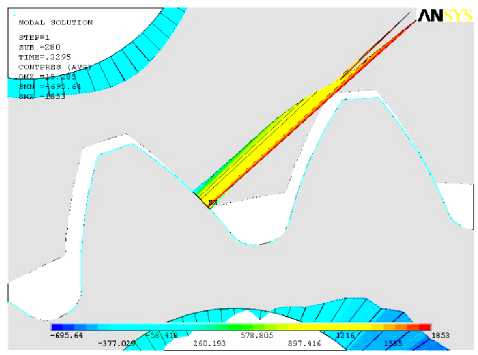
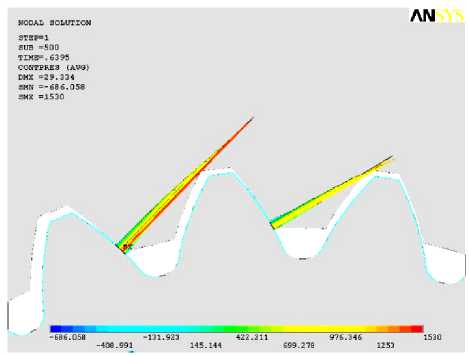
Рис. 9. Эпюра контактных давлений в процессе однопарного и многопарного взаимодействия зубьев проектируемой передачи

Таким образом, проектирование разномодульных зубчатых пар по предлагаемой методике с применением программного комплекса GearAnalysis показало возможность синтеза зубчатой пары внутреннего зацепления с малой разностью чисел зубьев, составленной из колес с внешним эвольвентным и внутренним шлицевым профилем и разными модулями. Минимизация кромочного эффекта в зацеплении и применение известных технологических приемов подготовки такой передачи к эксплуатации, включая эффективные технологии собственно формообразования зубьев, позволяет рассчитывать на расширение спектра применения такой передачи, что потребует проведения дополнительных исследований.