Проектно-баллистический анализ миссии длительного исследования астероида Апофис наноспутником с электроракетной двигательной установкой

Проблема исследования астероидов давно привлекает внимание ученых и общества [1–11]. В частности, проблема пролета астероида Апофис 99942 на угрожающем Земле расстоянии в 2029 году обсуждалась в работе [3]. Вместе с тем, значительно вырос интерес к длительным исследовательским миссиям, направленным на изучение физических свойств астероидов, комет и спутников планет [4–11], предусматривающих длительное пребывание в окрестности изучаемого тела. Например, в работе [8] приводится краткое описание современных и перспективных космических аппаратов (КА), создаваемых ФГУП «НПО им. С. А. Лавочкина» для фундаментальных исследований Луны, планет и малых тел Солнечной системы, предусматривающих выполнение маневров

в окрестности астероидов, в том числе сближение, посадку и возвращение грунта на Землю.

Вопросы проектирования гелиоцентрических перелетов КА к астероидам, особенно для КА с традиционными двигательными установками, достаточно хорошо исследованы. Например, в работе [12] подробно исследовано оптимальное управление КА с двигателем «большой тяги» для миссии Земля – астероид Апофис – Земля в классе многоимпульсных перелетов. Известно, что для длительных миссий наиболее эффективными, с точки зрения расхода рабочего тела, являются двигательные установки на базе электроракетных двигателей [10; 13–22]. К существенным характерным особенностям таких двигательных установок относятся малая тяга, создающая ускорение, сравнимое с гравитационными ускорениями от малых тел Солнечной системы, и длительное время функционирования (иногда до десяти лет). Поэтому для проектирования миссий с электрора-кетными двигательными установками (ЭРДУ) не-

К1ЛЕ АППАРАТЫ Ш

обходимо учитывать даже малые гравитационные возмущения, что особенно затруднительно для рассматриваемого класса баллистических задач, где уровни ускорений от тяги двигателя сравнимы с гравитационными возмущениями. Работы [15; 16; 19; 20; 22–25] посвящены оптимизации гелиоцентрического движения КА с двигателями «малой тяги», не допускающие использование импульсной постановки задачи.

Значительно слабее исследован вопрос об управлении движением КА в непосредственной близости от малого небесного тела неправильной 162 формы. Поведение КА в таком поле в значительной степени отличается от движения вблизи сфероидальных и эллипсоидальных тел, форма которых в некотором приближении может считаться правильной. Здесь нельзя использовать законы Кеплера и полученные на их основе программы управления. Отсутствие методики формирования программного управления может привести к существенным неопределенностям в определении запаса рабочего тела, необходимого для проведения миссии заданной продолжительности со всеми запланированными исследованиями. Даже поддержание постоянной орбиты у тела с нерегулярным гравитационным полем требует управления и затрат рабочего тела [7; 26–28].

Теоретическую основу исследования составляют работы, описывающие гравитационные поля малых тел Солнечной системы неправильной формы, а также работы о возможном поведении КА в окрестностях таких объектов [7; 26; 27; 29–32]. В данных исследованиях рассматривалась проблема поиска предельно точного способа формализации гравитационного поля астероидов в приложении к планируемым или уже осуществленным исследовательским миссиям, таким как NEAR Shoemaker, Hayabusa 1 и 2, Galileo, Cassini, Rosetta, Deep Space и др.

В качестве предлагаемых способов формализации гравитационного поля исследователями предлагаются следующие модели гравитационного потенциала: разложение потенциала в функциональный ряд (по сферическим, эллиптическим, эллипсоидальным функциям), модель пространственного многогранника и другие методы, основанные на оценке величины и направления гравитационного ускорения, действующего на КА.

Существенным недостатком данных моделей является их оторванность от задач баллистического проектирования и поиска оптимальных схем управления КА. Приведенные модели, в большинстве своем, требуют значительных вычислительных ресурсов и полного набора первоначальной информации о физической природе объекта исследования. На наш взгляд, последнее обстоятель- ство является существенным препятствием при предварительном проектировании миссии, осо-

Том 4

бенно при определении программ управления КА с электроракетными двигателями. Разработчиков реальных миссий к астероидам и кометам [33–35] ставит в затруднение необходимость при использовании этих моделей заранее знать физические свойства еще неизвестного до полета объекта исследования, его геометрию и распределение масс, в том числе внутреннее. В статьях [33–35] описываются значительные трудности при определении программного управления реальными миссиями Dawn и Rosetta. Неточности в определении программ управления при проектно-баллистическом анализе миссий приводили к существенному увеличению затрат рабочего тела на маневрирование, что снижало длительность самой ценной части миссии – собственно исследования небесного тела.

Традиционным подходом к проектированию миссии и проектного облика КА c ЭРДУ является минимизация массы рабочего тела, необходимого для перелета при заданных граничных условиях, определяемых целями исследования [10; 14; 36]. Именно такой подход к проектированию миссии предлагается использовать в данной работе. Для описания гравитационного поля исследуемого астероида предлагается использовать подход, описанный в [28], который позволит сформировать оптимальное программное управление для серии динамических маневров и провести проектнобаллистический анализ миссии в целом.

Проектно-баллистический анализ миссии длительного исследования астероида Апофис наноспутником

В данной работе рассматривается вопрос о реализуемости исследовательской миссии Земля – астероид Апофис, осуществляемой КА нано-класса с ЭРДУ. Предполагается, что КА выводится из сферы действия Земли с нулевым гиперболическим избытком скорости как попутный груз при осуществлении межпланетной миссии. Затем за счет собственной двигательной установки КА совершает гелиоцентрический перелет к Апофису, формирует рабочую орбиту и остается на ней длительное время.

В работе [37] показано, что на базе существующей элементной базы может быть разработан девятиюнитовый КА с начальной массой 9,8 кг, с ЭРДУ с номинальной тягой P = 2,1 мН, скоростью истечения c = 20000 м/c [38] и энергопитанием от панелей солнечных батарей (рис. 1).

В данной работе предлагается для предварительного баллистического проектирования миссии разбить ее на два участка. Первый – оптимальный по быстродействию гелиоцентрический перелет Земля – астероид Апофис с выравнивани- ем скорости КА и астероида. Второй – движение

в окрестности астероида, включающее оптимальный по быстродействию маневр формирования рабочей орбиты и поддержание рабочей орбиты в

течение заданного времени.

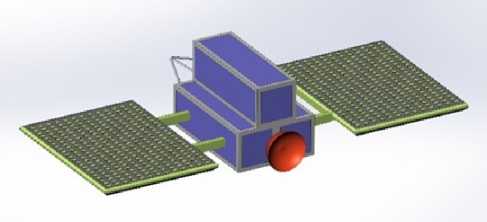
Рис. 1. Проектный облик КА с ЭРДУ нано-класса

существенное влияние на КА оказывает световое давление. В данной работе сделана попытка рассчитать в первом приближении необходимый запас рабочего тела для ЭРДУ и оценить возможность длительной миссии, поэтому возмущающие факторы не учитывались.

Граничные условия первого участка обеспечивают гелиоцентрический перелет КА от Земли к астероиду с выравниванием скорости:

Г3 (t 15 ) = Г4 (t 15 ), Г3 (t 1 f ) = rl(t1 f X r3 (t 15 ) = r4 (t 15 ), r3 (t 1 f ) = rl (tl f ),

На первом участке программа управления была получена с использованием принципа максимума Понтрягина с учетом гравитации Солнца, Земли и астероида (как материальной точки) в гелиоцентрической инерциальной системе координат. Уравнения движения в векторной форме имеют вид [37]:

d² r₁

dt2

-

^G ' m SUN

r1

-

G • mSC

r -

(r1 - r3

)

-

-

G • mE

³ r 1 - 4

( r 1 - ^r 4

) ,

_d2 _r

dt2

^G ' m SUN „ ^G ' m AST

з----r33-----( r3 - rl r3               rl-3

G • m

--3---(13 - r4 ) + a + f, r3-4

d2r4 dt2

^G "  m SUN „ G "  m AST ------3----^r4        3----- ^{( r}4 ^- r l ) , r 4                r l-4

dmSC dt

—

- 5 P

c

r E

V гз V

, a = — 5e mSC

Г р

V Гз V

.

где t1s – время начала перелета (соответствует дате и времени старта); t1f – время окончания гелиоцентрического перелета. Оптимальное по быстродействию управление, как показано в [14; 16; 25; 37; 41], обеспечивается работой ЭРДУ в течение всего времени движения (δ≡0) и направлением ускорения, доставляющему максимум га-^r мильтониану e =  3 ( Ψ – вектор сопряженных

I Тгз| множителей, соответствующих вектору скорости КА r3 ). Для численного решения краевой задачи (1–5) использовалась методика, описанная в работе [37] и реализованная в программном комплексе [42].

На втором участке движения, в соответствии с методикой [27], гравитационное поле астероида Апофис представляется как суперпозиция полей двух материальных точек массами тзз - ST = 1,539 • 1010 кг и тззл зТ зз 1,161.1010 кг, враща-AST                     AST ющихся с угловой скоростью собственного вращения астероида ( ω = 5,74 ⋅ 10 -5 1/c) на расстоянии d = 248 м (рис. 2). В [27] было показано, что при использовании такой модели погрешность в определении гравитационного ускорения астероида не превышает 10 % вплоть до поверхности астероида. Кроме астероида учитывалась гравитация Солнца и Земли.

Здесь m _SUN , m _E , m _AST , m _SC – массы Солнца, Земли, астероида и текущая масса КА соответственно; r ₁ , r ₃ , r ₄ – радиус-векторы астероида, КА и Земли относительно Солнца; r _1–3 – расстояния между КА и астероидом; r _1–4 , r _3–4 – расстояние от Земли до астероида и КА соответственно; a - ускорение от тяги КА; 5 е{ 1,0} - функция включения-выключения двигателя (1 – двигатель включен, 0 – выключен); e – единичный вектор направления тяги; f – возмущающие ускорения, действующие на КА. В работах [39; 40] проведен анализ динамики орбитального движения КА относительно астероида Апофис с учетом возмущающих факторов, в частности указано, что

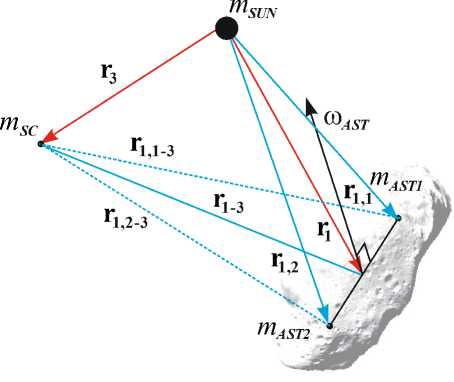
Рис. 2. К моделированию второго участка движения

KI/IE АППАРАТЫ Ш

Том 4

Движение центра масс астероида и Земли по-прежнему будет описываться уравнениями (1) и (3), а уравнение движения КА примет вид:

d ^r3 _ G • m sun

dt2

—

3 r3

r3

—

G ' m AST1

—

G • m

r 1,2 — 3

( r

—

^r 1,2 )

—

³ r 1,1 — 3

G • m E r3—4

^{( r} 3

—

^r 1,1 )

—

(гз — Г4) + a + f,

где r _1,1 , r _1,2 – радиус-векторы массивных точек астероида относительно Солнца; r _1,1–3 , r _1,2–3 – расстояния между КА и массивными точками.

Для определения управления на втором

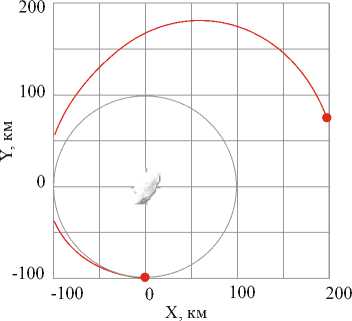
Рис. 4. Траектория формирования заданной орбиты радиусом 100 км

участке движения использовались две различные методики. Для определения управления, предназначенного для формирования заданной орбиты, – методика поиска оптимального по быстродействию управления, описанная в работе [43], а для длительного поддержания заданной орбиты использовался локально-оптимальный закон управления, поддерживающий постоянной большую полуось орбиты [28]. Эти методики полностью автоматизированы и реализованы в программном комплексе [44].

Результаты расчетов по участкам движения представлены в табл. и на рис. 3 (первый участок движения), 4 (формирование рабочей орбиты) и 5 (поддержание рабочей орбиты).

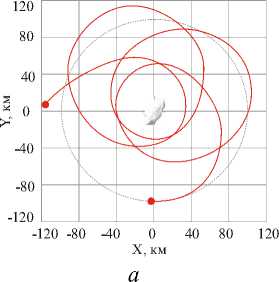
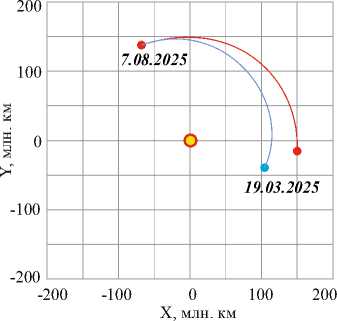
Рис. 3. Траектории КА и астероида на гелиоцентрическом участке движения

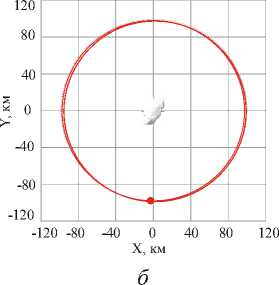
Рис. 5. Изменение траектории КА:

а ) – пассивное движение; б ) – движение под действием стабилизирующего орбиту управления

На рис. 3 траектория КА выделена красным цветом, астероида – синим. Рис. 4 иллюстрирует оптимальную траекторию формирования около-круговой орбиты радиусом 100 км относительно барицентра астероида. Астероид на рис. 4 и 5 показан схематически.

Рис. 5 а демонстрирует поведение КА относительно астероида Апофис без использования постоянно действующего корректирующего ускорения с начальными условиями, соответствующими невозмущенной круговой орбиты, а рис. 5 б – результат применения локально-оптимального управления, направленного на поддержание постоянным эксцентриситета орбиты.

Таблица

Баллистические характеристики участков движения

Маневр	Длительность, сут.	Расход рабочего тела, кг
Гелиоцентрический перелет	141,3	1,281
Формирование рабочей орбиты	4,38	3,97·10-3
Поддержание рабочей орбиты в течение суток	–	0,903·10-3

Как выяснилось, при длительных миссиях существенная часть рабочего тела расходуется на поддержание рабочей орбиты. Поэтому при предварительном планировании миссии нужно учитывать массу рабочего тела, необходимую на гелиоцентрический перелет и поддержание рабочей орбиты. Например, если считать, что исследования астероида в данной миссии должны продолжаться 10 лет, то на перелет к астероиду будет затрачено 1,281 кг, на формирование рабочей орбиты 3,97 гр., а на поддержание рабочей орбиты 3,29 кг рабочего тела.

Заключение

В статье анализируется проблема управляемого движения космических аппаратов вблизи объектов с нерегулярными гравитационными полями и рассмотрены конкретные баллистические характеристики миссии к астероиду Апофис. Моделирование движения проведено с разделением на два участка – гелиоцентрического движения и движения относительно астероида. Кратко описаны методики определения управления на участках движения и приведены результаты моделирования без учета возмущений, действующих на космический аппарат, и затрат на коррекцию навигационных ошибок. Показано, что с учетом этих допущений, космический аппарат массой 9,8 кг может осуществить задан-   165

ную миссию десятилетнего изучения астероида Апофис, израсходовав около 4,6 кг рабочего тела.