Профиль электрода для импульсных лазеров высокого давления

Самарский филиал Физического института им. П.Н.Лебедева РАН

Предложен полезный для экспериментальных и инженерных применений метод расчёта двумерных профилей электродов ТЕА лазеров, позволяющий прогнозировать изменение эффективной ширины разряда с изменением межэлектродного промежутка. Демонстрируются экспериментальные результаты по формированию пучков излучения в СО2-лазере с отношением поперечных размеров от 0,5 до 1.

При создании лазеров высокого давления (1 атм и выше) с самостоятельным импульсным разрядом одной из важных задач, требующих решения, является определение профиля электродов, которые обеспечивали бы разряд в объёме с нужными размерами, с максимально возможным энерговкладом и были достаточно компактны.

Имеется ряд работ [ 1-5 ] , в которых сформулированы как основные требования к профилю, так и даются конкретные рекомендации по профилированию электродов. Однако не всегда представляется возможным воспользоваться этими рекомендациями: получаемые профили либо громоздки, либо сложны в расчётах и изготовлении.

В настоящей работе предлагаются к рассмотрению двумерные профили электродов, рассчитанные методом эквивалентных зарядов [6] .

Исходная модель базируется на следующем. В качестве профиля электродов берутся эквипотенциали, образованные системой четырёх бесконечно тонких проводников, имеющих попарно противоположные, но одинаковые по величине плотности заряда, и расположенных в вершинах прямоугольника со сторонами 2 a х 2 b ; что эквивалентно системе из проводящей плоскости и находящихся на расстоянии b от неё двух одноимённо заряженных параллельных проводников с промежутком между ними равным 2 a . Отличие этой модели от рассмотренной в [3,4] заключается в отсутствии соленоидальных источников.

На рис.1 показаны эквипотенциали и проводники в нижней полуплоскости ( x,y) . Проводники проходят перпендикулярно плоскости рисунка. Очевидно, что при сближении одноименных зарядов будет изменяться величина неоднородности поля в средней области. Наличие простой физической наглядности и привлекло наше внимание к этой модели. Потенциал, создаваемый этой системой проводников равен:

r ■ r₂

U = ^- q ■ In-----,           (1)

,

'3 'а где q - заряд на единицу длины, г. - расстояние от точки пространства (x,у) до i-го проводника.

Тогда уравнение эквипотенциалей будет иметь вид:

(t + h2) (k + .)=c2^t;+h)©+h), (2) где c - постоянная, k = x + a, k = у + b, 1                             1

k„ = x - a , k = у - b. 2                  2

Данное уравнение можно представить в виде биквадратного относительно х, из которого получаем окончательное выражение для эквипотенциалей в следующем виде:

х = ±^- (у² + 2bdy + b ² + a ²) ± 2 M , (3) где

M = у ² ■ ( b² d ² - l ² ) - 2a² bdy - a ² b ²

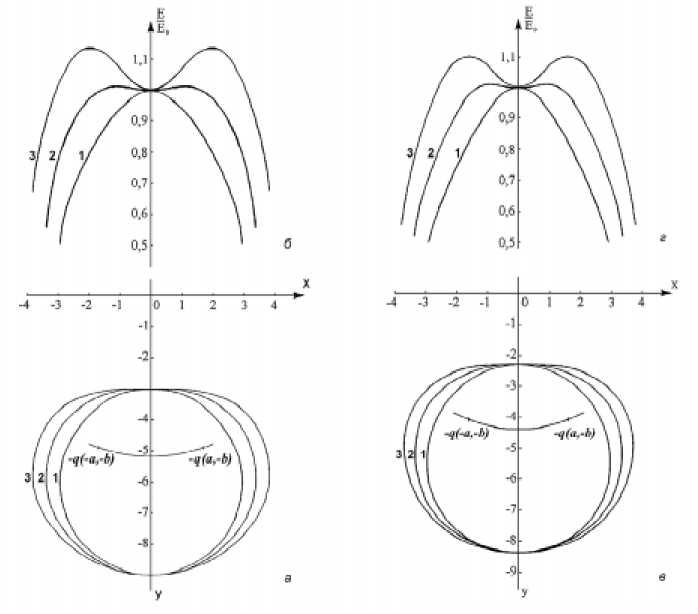
Рис.1. (а) эквипотенциали (1, 2, 3) с параметром а =(0; 1,2; 1,732)см соответственно; У 1 =-3см, У₂=-9см; (б) распределение поля (1, 2, 3) на поверхности эквипотенциалей (1, 2, 3)(а) относительно величины поля в вершине (x=0). Неоднородность в максимумах составляет: 1,3% - (2), 13,5% - (3); (в) эквипотенциали (1, 2, 3) с параметром а =(0; 1,15; 1,579)см соответственно; у=-2,3см, у₂=-8,3см; (г) распределение поля (1, 2, 3) на поверхности эквипотенциалей (1, 2, 3)(в) относительно величины поля в вершине (x=0). Неоднородность поля в максимумах составляет: 0,6% - (2), 10% - (3)

d =

С ² + 1

2 c -

2       2      2

1 l = a + b •

,

Выделим важные с практической точки зрения свойства эквипотенциалей, представляющих интерес как профили электродов для лазеров. Обозначим у_ру - точки пресечения оси 0Y эквипотенциалью.

Имеем следующее соотношение:

'.■'.         ."                                                      ,2

^С = У, + У 2 + Ь ' ^1 ' ^У = a ^{+ Ь} = ^l ■ y - по абсолютной величине совпадает с межэлектродным расстоянием в случае электродной пары плоскость-профиль. При фиксированных значениях у₁ и l уравнение(З) будет описывать профили равной толщины, но с различной величиной неоднородности поля на поверхности профиля в области межэлектродного зазора.

При фиксированных значениях y1, l можно выделить следующие типы экви- потенциалей:

• I .    a = 0, эквипотенциали - окружности.

Максимум напряжённости поля в вершине электрода, явно выраженная неоднородность в распределении поля по поверхности электрода (кривые 1, рис.1а, в).

• II.    a = 2 |% ⁺ У 2 ^- V У 1 • У 2 .

Максимум напряженности поля в вершине электрода, но с более равномерным распределением по сравнению со случаем I .

¹    У 1 i        V

• III.    a =~J~' ^{( У}1 — ^У 2 )

² V У 2

- профиль с

радиусом кривизны в вершине R = ^ (ква-зиплоский электрод). Поле имеет два бобковых максимума. Величина неоднородности по отношению к вершине составляет, как правило (10-13)% (кривые 3 рис.1а,1в).

В ряде конструкций электродов такая неоднородность поля может оказаться избыточной [7]. В нашем случае этого не наблюдалось. Тем не менее, выбирая значения а в пределах:

• 1                                     1 ------------------------

• -|У1 + У2I- 7У1 • У2 <а<- з ~ • (Уг - У1)2 2                        2 V У 2

(кривые 2 рис.1а,в), и, задаваясь необходимой степенью неоднородности в боковых максимумах, можно надеяться сформировать однородный разряд с требуемым по ширине размером.

Отметим, что поле на аноде ( у =0) изме-

2      2       4          2      2   2     4

няется как ( x + l )/( x + 2( b - a ) x + l ) и при b² } 3a² не имеет боковых максимумов, кроме центрального. В рассмотренных случаях это условие выполняется. Ввиду перехода распределения поля с двумя максимума на катоде на распределение с одним центральным максимумом на аноде, ширина зоны разряда, по-видимому, будет несколько меньше, чем расстояние между катодными максимумами.

Рис.1в иллюстрирует случай, когда экви-потенциали проходят через другие точки у ₇, у ₂ , но имеют то же значение у 1 - у ₂ . Экви-потенциали 2 (рис.1а и рис.1в) почти совпадают при наложении. Если учесть, что точность изготовления профиля, как правило, составляет несколько десятых мм, то можно считать, что эквипотенциали 2 с осью 0 Y описывают сечение одной и той же электродной пары, но с различным межэлектродным расстоянием и с различным распределением поля по поверхности. Это дает основание полагать, что электрод, изготовленный по некоторым профилям в соответствии с уравнением (3), перемещением вдоль оси разряда можно выставить в положение с необходимой однородностью поля по поверхности электрода.

С целью проверки работоспособности модели нами был выполнен электрод, соответствующий случаю кривых 3 рис.1 для межэлектродного расстояния 2,5 см. Торцы электродов обрабатывались по тому же профилю с плавным сопряжением привершинных по верхностей. В качестве анода использовалась плоская плита значительно превосходящая по ширине катод. Этот тип профиля катода был выбран из-за возможности дальнейшей доработки при необходимости под профиль близкий случаю кривых 2 рис.1.

Электрод устанавливался в ТЕА СО2 -лазере с межэлектродным расстоянием (2,3; 2,5; 2,7; 3) см. Форма сечения пучка излучения регистрировалась на термобумаге и приведена на рис.2. Резонатор состоял из глухого зеркала с радиусом кривизны 40 м и плоского полупрозрачного с расстоянием между ними 1,2 м. Длина активной зоны составляла 90 см.

Легко видеть, что размер пятна излучения монотонно увеличивается с увеличением межэлектродного расстояния. В промежутке (2,5-3) см характерный размер поперечного сечения излучения примерно равен межэлектродному расстоянию. При межэлектродном расстоянии 2,3 см активная зона заужена, разряд имеет тенденцию срываться в искровой при энерговкладах в разрядную зону характерных для больших межэлектродных промежутков (80-120) Дж.

Таким образом мы имеем наглядную демонстрацию работоспособности и полезности рассмотренной выше модели, позволяющей определить практически и конструктив-

Рис.2. Вид поперечного сечения пучка излучения для различных межэлектродных расстояний: (а) - 2,3см; (б) - 2,5см; (в) - 2,7см; (г) - 3см.

но подобрать необходимые виды профилей, тем самым спрогнозировать реальные экспериментальные ситуации.

Как показывает наш практический опыт работы с TEA СО2-лазерами, выявленная в рамках модели закономерность, по-видимо-му, является более общей и может выполняться для электродов, изготовленных со значительным отклонением от профиля, задаваемым уравнением (3).