Профили скоростей и теплообмен при турбулентном течении несжимаемой жидкости в гладкой круглой трубе немалого диаметра

Существует тесная связь между турбулентностью вязкой жидкости и находящимися в ней вихрями. Переход жидкости из ламинарного режима течения в турбулентный у твердой стенки сопровождается образованием когерентных вихревых структур, называемых Λ-вихрями, или подковообразными вихрями [4], [16], которые в развитом турбулентном течении вблизи твердой стенки образуют устойчивую, плотно упакованную систему [16].

Наблюдаемая в экспериментах связь между турбулентностью и вихревыми структурами стимулировала создание моделей турбулентности, которые тем или иным способом учитывают эту связь. Эти модели называют моделями вихревой турбулентности [1], [8], [17]. Одной из таких моделей является рассматриваемая здесь наша модель [1], [2], предназначенная для описания турбулентных течений в слое, непосредственно прилегающем к твердой поверхности (стенке). В ней

пристеночные структуры рассматриваются как носители локальной вихревой анизотропии, определяющей как турбулентную вязкость, так и турбулентную теплопроводность среды. В связи с этим данная модель называется моделью анизотропной вихревой турбулентности.

В настоящей работе модель пристеночной анизотропной турбулентности [1], [2] используется для решения двух задач – об определении поля скоростей и поля температур при установившемся турбулентном течении несжимаемой жидкости в круглой трубе. Пристеночный слой вихревой турбулентности имеет довольно небольшую толщину, порядка нескольких сантиметров [13], [16], поэтому во всем потоке модель можно применять только в тех случаях, когда толщина пристеночного слоя достигает оси трубы или близка к ней. В трубах больших диаметров поток необходимо делить на две части – пристеночный слой и ядро течения, подобно тому, как это делается в [5], [10]. Если пренебречь влиянием теплообмена на течение жидкости, то задачи об определении полей скорости и температуры можно решать раздельно [9], [10], что и будет сделано ниже.

Уравнения модели анизотропной турбулентности. В модели [1], [2] пристеночное турбулентное течение вязкой жидкости рассматривается как движение анизотропной среды, анизотропию которой создает система Λ-вихрей. Λ-вихрь имеет вершину как наиболее удаленную от стенки точку вихря и две ветви, убегающие вниз по потоку. При удалении от вершины ветви приближаются к стенке, в пределе располагаясь вдоль нее. По наблюдениям [13], [16], угол наклона вихря к направлению течения у вершины в среднем равен 40–45°. Согласно [16], вихри создают статистически равное, противоположное вращение, так что среднее значение продольной завихренности равно нулю. В этой ситуации одной из характеристик структуры в точке, влияющих на течение жидкости, является среднее направление вихревых линий, характеризуемое вектором n , который, вообще говоря, может быть как единичным, так и произвольной длины, в зависимости от того, учитывается или не учитывается плотность вихревых линий. Вектор n называется директором.

Все локальные величины, характеризующие состояние и движение среды, в модели [1], [2] по определению считаются осредненными по объему. Кинематическими параметрами среды в точке являются скорость u и директор n единичной длины. При таком определении турбулизованная жидкость может рассматриваться как ориентируемая жидкость, модель которой, нацеленная первоначально на описание динамики жидких кристаллов, построена в [11], [15]. Уравнение неразрывности и уравнения движения несжимаемой ориентируемой жидкости в декартовых координатах x i имеют вид

5 U a _ 0

dXa’ dUi   dPia, p— _-^—+ pfi, dt d ( dni ) двц

P^LI J~;“ I + gi + PGi, dt ^ dt )d

где ρ – плотность жидкости, u i – скорость, p ij – напряжения, f i – плотность массовой силы. Уравнение (3) является характерным уравнением движения ориентируемой жидкости [11], [15]. Величины β_i j , g_i , G_i называются соответственно обобщенными напряжениями, обобщенной внутренней и обобщенной внешней массовой силой. Параметр J характеризует осредненную инерционность структуры при повороте элементов вихревых нитей. Здесь и ниже по повторяющимся индексам предполагается суммирование от 1 до 3.

Определяющие уравнения учитывают специфику среды. Для турбулизованной жидкости вблизи стенки они имеют вид [1], [2]

Pij _-P pj + T + тij,(4)

Tij _ Kna,i(nj,a - Пa,j + ^Пpna,p) ,(5)

тij _ pananpeapninj + ^ij,(6)

Pij _ j + K(ni,j - nj,i - njnani,a) ,(7)

gi _ Xn - (Kpni),в +Knanp,anp,i ,(8)

d n i           1 ^ S u i

, eij _+ dxj         2 (dxj где р – давление; μ0, μ1, K – коэффициенты модели; δij – символ Кронекера; χ и κi – произвольные скалярная и векторная функции соответственно. Поскольку свойства жидкости вблизи твердой стенки определяются пристеночной вихревой структурой потока, коэффициенты μ0, μ1, K могут зависеть от параметров, глобально характеризующих течение, например от числа Рейнольдса.

Для исследования изотермических течений уравнений (1)–(8) достаточно. Однако при решении задачи о теплообмене их необходимо дополнить уравнением притока тепла [15]:

p—_ Pijeij+pijNij - giNi+Q - ^q^, (io) dt                               dxi где U – внутренняя энергия, отнесенная к единице массы, Q – интенсивность источника тепла, qi – плотность потока тепла. Кинематические параметры Ni, Nij определяются формулами:

N i — n & i ^ i a n a , N i , j — n & i , j ^ i a n a , j

2 ^ij     u i , j" ^uj , i ,

U i _

dn i dt ^.

Профиль скоростей. Пусть в бесконечной прямой круглой трубе радиуса R в режиме установившегося турбулентного течения движется вязкая несжимаемая жидкость. Введем цилиндрическую систему координат r , φ, x с осью x по оси трубы в направлении течения. Область течения зададим как объединение ядра течения 0 ≤ r <  r 0 и пристеночной области r 0 ≤ r ≤ R. Найдем вначале профиль скоростей в пристеночной области. Предположим, что коэффициенты μ 0 , μ 1 , K и инерционный параметр J при заданных условиях течения постоянны. Пренебрегая внешними массовыми силами f i и G i , скорость u i и директор n i будем искать в виде

U x _ U ( r ), U r _ U p _ 0, U x _ cos 0 (r ), n_r _ sin ^ ( r ), n _p _ 0,

где θ – угол между директором n i и осью х .

Подстановка выражений (12) в уравнения (1)–(8) с учетом сделанных предположений при- водит к необходимым для решения задачи уравнениям. Уравнение неразрывности (1) удовлетворяется тождественно. Пользуясь произволом χ и κi в формулах (7) и (8), положим их равными нулю. В результате из уравнений (3) получим одно уравнение для θ (r) в виде [1], [2]

3 bR - 1 1

F ⁽ t ) ^— 2 _{Y 2} -₁ N y ^{2 - 1 arc}tg

t

V Y ² -1

+ Y in ■

2 Y + t

+

sin 9 cos 9 l 9 " +   I- (2 - 3cos² 9 ) 9'’ — 0.(13)

( r J

1 + 2e ,

+--------- in

4(2 Y ² - 1)

A — -P l_ 3 Ц 1 b ² R

Y ² - 1 ²      1,

—-----+ -in t2 + y 2 -1 4

t ⁴ - 1 ² - ^ + - , 2

u. — Tw, e — Y0-, 2.Y2 — 1 + V1 + 4e, V p      2^1

Здесь и далее штрихами обозначены производные по координате r .

Уравнения (2), (4)–(6), совместно с (12) после небольших преобразований дают уравнение для профиля скоростей u ( r ) [1], [2]

ц ₁sin² 9 cos² 9 + ^2-

r u — —Tw , R

где τ w – модуль касательного напряжения на стенке трубы.

Для трубы с гладкими стенками граничные условия прилегания вихревых линий к стенке и прилипания жидкости к ней имеют вид

где u . - динамическая скорость.

При определении профиля скоростей в ядре течения, как и в [5], [10], воспользуемся предположением о постоянстве турбулентной вязкости в ядре при фиксированных числе Рейнольдса и радиусе трубы. Условием сращивания профилей является равенство турбулентных вязкостей на границе областей r = r 0 . Как видно из уравнения (14), динамическая турбулентная вязкость в пристеночном слое задается формулой

Ц т — ^sin² 9 cos² 9 + 1 Ц о .          (20)

9 — R — 0, U_V — R — 0.

Первое интегрирование уравнения (13) дает rsin 9cos2 99' —-bR,            (16)

где (– b ) – постоянная интегрирования, которую на данном этапе исследований приходится определять экспериментально; перед b взят знак минус, чтобы b > 0. При сравнении решений ряда задач с опытными данными для воздуха выяснилось, что b = 4,83 м^-1 [3].

Интегрируя уравнение (16) с первым граничным условием (15), имеем

На рис. 1 даны графики зависимости безразмерной кинематической турбулентной вязкости N — Ц т /( p u . R ) от безразмерного расстояния от стенки η = (1 - ξ) при течении воздуха (плотность ρ = 1,205 кг/м³, кинематическая вязкость ν = 1,50·10^-5 м²/с) в трубе диаметром d = 247 мм и числом Рейнольдса Re = 40260 (Re = wd/ ν, где w – средняя скорость). Кривая 1 – расчет по формулам (20) и (17) при b = 4,83 м^-1, μ 0 = 1,85 ·10 ^–6 Па · с, ц₁ = 0,047- u . Па^с, [3]; кривая 2 - аппроксимация [19] опытных данных Лауфера [14]; кривая 3 – график эмпирической формулы Рейхардта [18]

r cos3 9 — 1 + 3bR In 5,    5 — R.          (17)

Вблизи стенки трубы функцию lnξ заменим первым членом ее разложения в ряд Тейлора – функцией (ξ – 1), тогда получим

N — 0.0666 [ 1 - (1 - п ) ² ][ 1 + 2(1 - П ) ² ] .      (21)

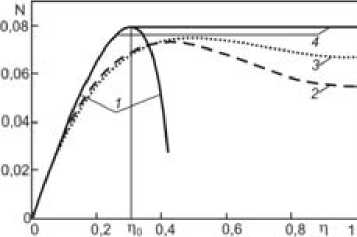
Рис. 1

cos 9 — [ 1 - 3bR(1 - ^ ) ] ^V3 .            (18)

Подстановка формулы (18) в уравнение (14) и интегрирование его затем со вторым граничным условием (15) дают искомый профиль скоростей в пристеночном слое:

u — Au . [ Ф ( £ ) -Ф (1) ] ,

Ф 5 ) — F(t ( 5 )),                         (19)

t ( 5 ) — [1 - 3 bR (1 - 5 )p,

В пристеночной области графики аналогичны: все кривые монотонно растут, достигая в близких точках близких максимальных значений. За точкой экстремума кривая 1 резко падает, тогда как кривые 2 и 3 показывают слабое падение за точками экстремума при приближении к оси потока. Существование точки экстремума на графиках N (η), особенно явное на кривой 1 , дает основания определить границу между пристеночным слоем и ядром течения как поверхность r = r 0 (на рис. 1 точка η 0 = ( R - r 0 )/ R ), на которой

турбулентная вязкость (20) достигает максимального значения. Очевидно, в этой точке угол θ = 45°, что вполне согласуется с максимальными наблюдаемыми значениями углов наклона пристеночных вихрей [13], [16].

По условию сращивания скоростей на границе областей постоянную турбулентную вязкость в ядре μ T 0 определим как μ T 0 = μ T (η 0 ), где μ T – функция, определяемая формулами (20) и (17). На рис. 1 принятой по всему сечению трубы вязкости соответствует кривая 4. Максимальное значение μ T 0 и точка максимума η 0 имеют значения:

Ц 1   Ц о

^{Ц то} = 7⁺ у,

П о = 1 - exp

' У2 - 4 '

I ^12bR )

Если угол θ определен приближенной формулой (18), то

П о =

4 - У2

12 bR

Графики зависимости N (η), очень близкие и качественно, и количественно к кривой 4 , другими подходами получены в [5], [17].

При постоянной турбулентной вязкости профиль скоростей в ядре течения 0 <  £ <  ^ _о имеет вид

— = u ⁰ + _±_ ( ^ 0 - ^ 2 ) , N o = ^, u . и . 2 N о                 р u . R (24)

и о = Au * [ Ф ( ^ о ) -Ф (1) ] .

На рис. 2 для примера представлены профили скоростей при течении воздуха в трубе диаметра d = 247 мм при числе Рейнольдса Re = 40260. Точками обозначены результаты экспериментов Лауфера [14]. Расчетный профиль скоростей (19), (24) (кривая 1 ) найден в условиях эксперимента и при тех же расчетных значениях для b , μ 0 и μ 1 , которые использованы в расчетах для рис. 1. Кривая 2 – график эмпирической формулы [9]

и 1 . _л х        о,29 к у +

— = — ln(1 + к у+) +-------------+ и. к             1 + о,о935(к у+)2       (25)

+    П ^{У +}Г^ [ 1 + 6 П- (1 + 4 П ) п ] ,

1 + к ( у + / п )

( R - r)и .

У + =-------- v при κ = 0,41 и Π = 0,2. Кривая 3 – график эмпирической формулы [10]

u и.

( и max / и . ) + 2,44ln( n ) - о,8 при о <  п <  о,15

( и max / и . )- 7,8(1 - п ) ² при п >  о, 15

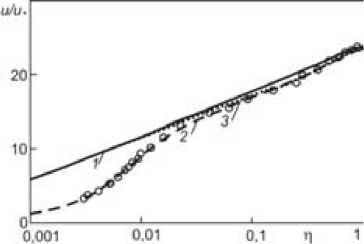
Рис. 2

Очевидно, за исключением очень узкой области, прилегающей к стенке трубы, расчетный профиль близок как к опытным точкам, так и к графикам формул (25), (26).

Из формулы (22) следует, что при уменьшении радиуса трубы R относительная толщина пристеночного слоя растет, достигая в пределе единицы при стремлении радиуса к нулю. В этом случае область, занимаемая ядром, сужается, так что, не делая большой ошибки, все течение в трубе можно считать анизотропно турбулентным, определяя профиль скоростей во всей области течения формулами (19). Трубы, в которых профиль скоростей (19) имеет место во всей области течения, естественно назвать трубами малого диаметра. Для максимального радиуса труб малого диаметра R max формула (22) дает значение R max = 0. Однако, если воспользоваться приближенной формулой (23), получим R max = (4 – √2)/(12 b ). Для течений воздуха R max ≈ 45 мм, причем при этом значения радиуса из формулы (22) следует η 0 = 0,63. Использование модели во всей области течения в трубе малого диаметра хорошо согласуется с результатами экспериментов. На рис. 3 приведены расчетные профили скоростей 1 и 4 , полученные соответственно по формуле (19) по всему сечению и формулам (19), (24) двухслойной модели для течения воздуха в трубе диаметром d = 120 мм при числе Рейнольдса Re = 40000; на рисунке графики совпадают. Кривые 2 и 3 соответственно являются графиками эмпирических формул (25) и (26), полученных при тех же значениях параметров.

Этот факт, по-видимому, можно объяснить тем, что модель не учитывает наличие в структуре вихрей разной длины, так называемой «иерархии вихрей» [16], а ограничивается средним уровнем.

и/и.

qE ------------1-------------1-------

О.ОО1 0,01            0.1 И

Рис. 3

Предложенная в работе [10] формула (26) также предполагает двухслойность турбулентного течения, что очевидно из самой формулы. Однако природа двухслойности осталась не до конца проясненной, поэтому и толщина пристеночного слоя η ≤ 0,15 воспринимается просто как результат подгонки при обработке опытных данных.

Теплообмен. Имея выражения (19) и (24) для турбулентного профиля скоростей в трубе, можно приступать к решению задачи о теплообмене. Найдем установившееся распределение температуры в полубесконечной трубе х ≥ 0 с постоянной температурой стенки T w . В принятой системе координат r , φ, x температуру T отыскиваем в виде T — T ( r , x ). Как и при определении профиля скоростей, задача о распределении температуры в пристеночном слое и ядре течения рассматривается отдельно.

В пристеночном слое движущаяся среда (турбулентная жидкость) имеет локальную симметрию, задаваемую директором n i , поэтому с учетом зависимости T ( r , x ) закон Фурье записывается в виде

В ядре течения коэффициент турбулентной теплопроводности λ T 0 , как и турбулентную вязкость, будем считать постоянным и равным турбулентной теплопроводности λ _T на границе областей ξ = ξ 0 :

A t o — A o + . T 00 2

Тогда уравнение распространения тепла в ядре течения имеет вид

, (д ²T , i д T )         , дТ T

A t ol— + -— I ^— p C p U ⁽ r )—.      (3i)

V д r ² r д r )           д x

Пусть T ₀ = const – температура во входном сечении x = 0. Введем безразмерные переменные

0 —

T - T w

T o - T w

r

^{6 —}ii’

X

X — J^. (32)

„ , , . дT , дT qr — -(Ao + Ai n2) —--Ai nrnx ——, д r

. ( д T д T) q^ — A1 Пф I nr “ + nx “ I , V д rд

,    дTT qx — -Ainxnr —--(Ao + Ai n2) —, д rд

Уравнения (29) и (31) можно рассматривать как одно уравнение во всей области течения, которое после подстановки в него соответственно профилей скоростей (19) и (24) в безразмерных переменных (32) имеет вид

A^ + ^Ti ( 6 ) д 6 ²

д 0 д 6

— ^ 2 ( 6 )

д 0 д X,

где (q r , q φ , q x ) – поток тепла , λ 0 и λ 1 – коэффици енты модели , характеризующие турбулентную теплопроводность среды . При фиксированном режиме течения коэффициенты λ 0 и λ 1 считаем постоянными .

Если пренебречь теплопроводностью в на правлении течения , то коэффициент турбулент ной теплопроводности λ _T в пристеночном слое определяется формулой

A t — A o + A i n r ² — A o + A i sin² 9 . (28)

Пусть внутренние источники тепла отсутствуют: Q = 0. Тогда, сделав обычные в подобных задачах предположения [6], из уравнения (10) с учетом формул (27) получим уравнение распространения тепла

. . . д² T

(Ao + Ai sin2 9)—- + v                / д r 1

A o + A i sin² 9 , , . _пп^д T

--+ A _i sin 2 99 I— — r                  ) д r

„     ( i д T

• ^— p c p u ⁽ r ) —, д x

  
  

где c_p – удельная теплоемкость при постоянном давлении.

Т 2 ( 6 )

• p c p u ^{( 6 )} R

o <  6 <  6 o ,

, 6 o <  6 <  i.

Уравнение (33) должно удовлетворять граничным условиям

0 ( 6 , o) — i , 0 (i, X ) — o, ^{д0 (}°’ X ) — o    (34)

д 6

и условиям сращивания решений на границе областей ξ = ξ 0

0 ( 6 o - o, X ) — 0 ( 6 o + o, X ),

T0 ( 6 o - o, X ) T0 ( 6 o + o, X )         (35)

-----д 6 -----⁼-----д 6-----•

Равенства (35) выражают равенство температур и потоков тепла при переходе через границу ξ = ξ 0 .

Функции Ψ 1 (ξ) и Ψ 2 (ξ) в уравнении (33) на границе ξ=ξ 0 , очевидно, разрывные. Однако вследствие первого условия (35) на границе слоев решение Θ (ξ, Χ) должно быть непрерывно.

Как и в [3], решение уравнения (33) будем искать приближенно, методом Галеркина, в виде

n

0 ( 5 , X ) = 2 g k ( X ) ф к ( 5 ),           (36)

к = 1

взяв здесь в качестве базисных непрерывные функции φ k (ξ), удовлетворяющие второму и третьему граничным условиям (34) и первому условию непрерывности (35):

фк(5) = Фo(5)cos ((k -1) n5), к = 1, 2 , . . [Fo(5) - Fo(1) ,

., n ,

Ф о ( 5 ) ЧФ о ( 5 о )

u( 5 o ) + ^1^( 5 2 - 5 ² ) , 2 N о          _

^{0 - 5}< ^5о (37)

I u ( 5 о ) L

F o ( 5 ) = 2(3 bR - 1)ln ^-^{1 5} + Y + 1 ( 5 )

+ ln 2 Y. ¹ 2 ^{5 )} + ln 1 4 ( 5 ) - 1 2 ( 5 ) - * 1 + 2 1 2 ( 5 ). 1 2 ( 5 ) + Y ² - 1

где t (ξ) – функция, определенная третьей формулой (19). Функции g k ( X ), удовлетворяющие первому граничному условию (34), определяются стандартной процедурой метода Галеркина [7].

Формула (36) дает приближенное решение задачи. Местное число Нуссельта Nu = α d /λ можно вычислить затем по формуле [9], [10]

2 Л , fd0) Nu = ,

*5 J 5 = 1

0 (X) = -J0 ( 5 ,x)u( 5 ) 5 d 5 , w 0

где α – коэффициент те п лоотдачи, λ – коэффициент теплопроводности газа, 0 - средняя массовая температура по сечению и w – средняя скорость в трубе.

Для сравнения с опытными данными решение (36) было реализовано при конкретных условиях. Жидкость – воздух: ρ = 1,205 кг/м³, ν = 1,5·10^–5 м²/с, λ = 2,57·10^–2 Вт/(м · К), с p = 1002 Дж/(кг · К), число Прандтля Pr = 0,705. Коэффициенты модели те же, что были найдены из сравнения с опытными данными для труб малого диаметра [3]: 2 о = о,28 R и . Вт/(м • К), Х 1 = 46,5 и . Вт/(м • К). Расчеты проведены при n = 25.

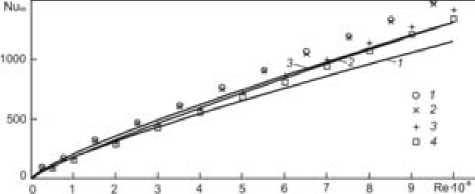
Рис. 4

В результате расчета получены значения предельного числа Нуссельта Nu „ = NuI X = 200 при числах Рейнольдса вплоть до Re = 10⁶ в трубах диаметров d = 100; 200; 300; 400 мм (точки на рис. 4). Для сравнения на рисунке приведены также графики эмпирических формул: кривая 1 [9]

f RePr/8

Nu „ =------------j=

1+Г+"Yf'Pr'3-)"

кривая 2 [10]

Nu„ = 7,6 - 3,6- + 0,0096Re0,87Pr0,605 ;(40)

lg Re кривая 3 [12]

Nu „

Re Pr f 2

4,24 ln(Ref16) + 25,0Pr ²/³ + 4,24ln Pr - 20.2

где f = (1,82lg(Re/8)f .

Графики на рис. 4 позволяют отметить следующее. Во-первых, эмпирические формулы (39)–(41) не вполне эквивалентны друг другу. Если формулы (40) и (41) дают близкие значения практически во всем диапазоне чисел Рейнольдса, то формула (39) близка к ним примерно до Re = 3 - 10⁵. Во-вторых, расчетные значения зависимости Nu ∞ (Re) зависят от диаметра трубы. Однако разность значений Nu ∞ для труб диаметра 100–400 мм при одном и том же числе Рейнольдса невелика (не более 6–7 % от среднего значения), так что в экспериментах такая разность может рассматриваться как ошибка эксперимента, а сами значения зависимости Nu ∞ (Re) как независящие от диаметра.

ВЫВОДЫ

Модель анизотропной турбулентности является базой для рассматриваемой двухслойной модели турбулентного течения и теплообмена в трубе. С использованием ее характерного параметра – директора – вводятся определяющие уравнения пристеночной турбулентности и теплопроводности, коэффициенты турбулентной вязкости и теплопроводности в ядре течения, а также граница между пристеночной областью и ядром течения. При решении задач и последующем сравнении результатов решений с опытными данными были использованы устойчивые зависимости для коэффициентов модели, которые были найдены ранее при решении других задач и которые можно рассматривать как характерные для среды.

В заключение автор выражает искреннюю благодарность В. Н. Николаевскому за внимание к работе и ценные замечания.